基于切換網絡的一類適型分數階耦合非線性系統的穩定性

高揚，龐棋月

基于切換網絡的一類適型分數階耦合非線性系統的穩定性

高揚1，龐棋月2

（1. 大慶師范學院 數學科學學院，黑龍江 大慶 163712；2. 東北石油大學 數學與統計學院，黑龍江 大慶 163711）

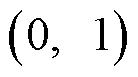
Caputo導數；適型分數階導數；分數階指數穩定；Mittag-Leffler型穩定

1　引言及預備知識

由于在物理和工程領域的強大應用性，分數階微積分理論得到廣泛關注[1-4]．2014年，Khalil[5]等提出一個新的分數階導數，命名為適型分數階導數，同3種常見的Riemann-Liouville型、Grunwald型和Caputo型分數階導數相比，適型分數階導數更接近實際，因而一經提出就引起了廣泛關注[6-8]．近年來，雖然一些學者已經著手建立適型分數階系統微積分理論，但是基于適型分數階導數的穩定性理論研究結果還較少．比較經典的是文獻[8]，建立了適型分數階非線性系統的穩定性與漸進穩定性Lyapunov理論．

文獻[9]研究了基于網絡的分數階微分方程耦合系統

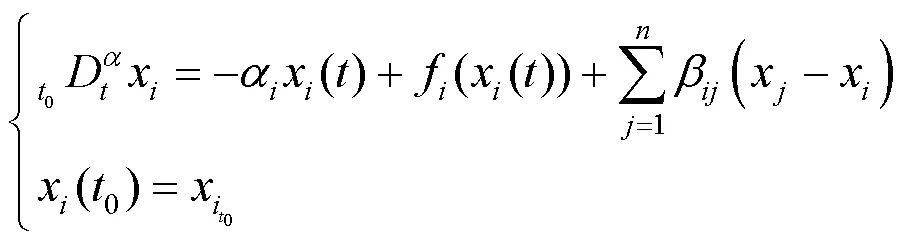
考慮適型分數階微分方程系統

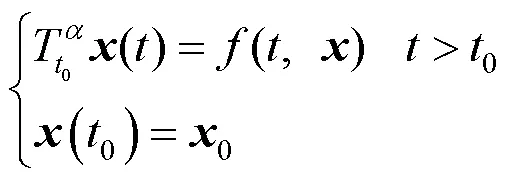
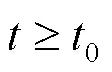
2　主要結果及證明

考慮適型分數階切換線性系統

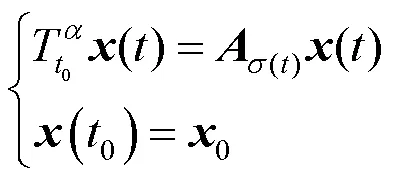
定理1假設系統（3）滿足條件：

則系統（3）為分數階指數穩定的．

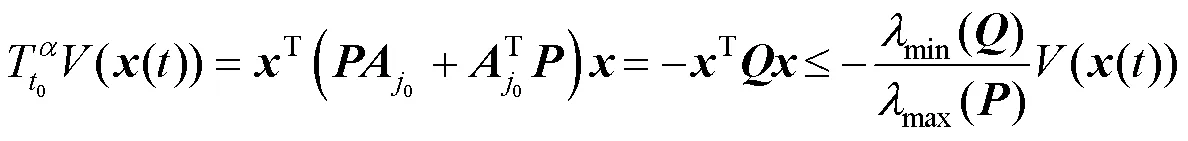
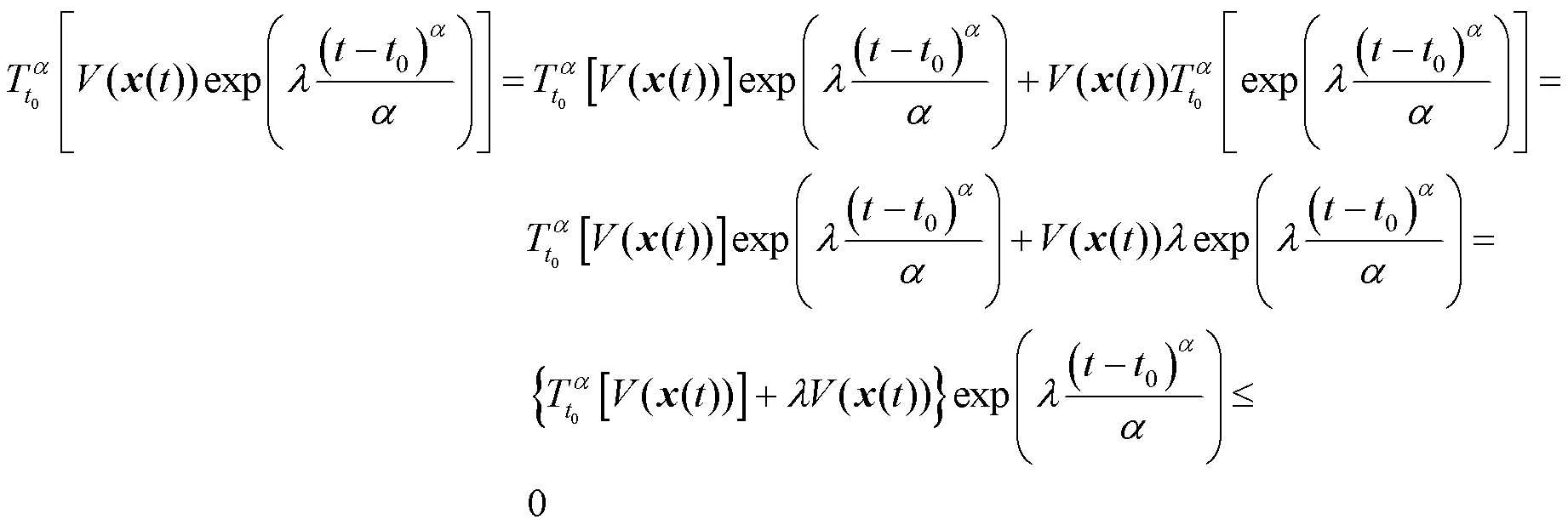
證畢．

本文在文獻[5-6]的基礎上進一步推廣，從2個方面進行探索：（1）用適型分數階導數取代Caputo導數；（2）考慮網絡頂點之間關系依賴時間，也就是引入切換拓撲情形．

考慮適型分數階系統

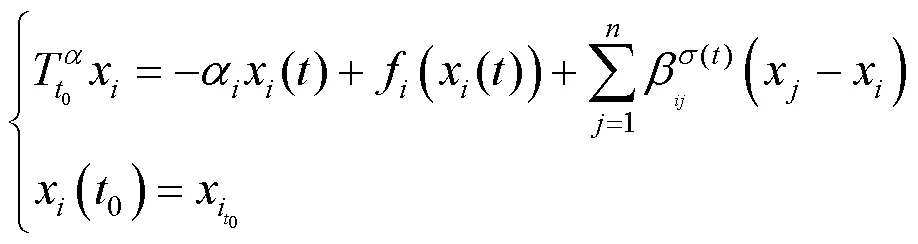
定理2若系統（4）滿足條件：

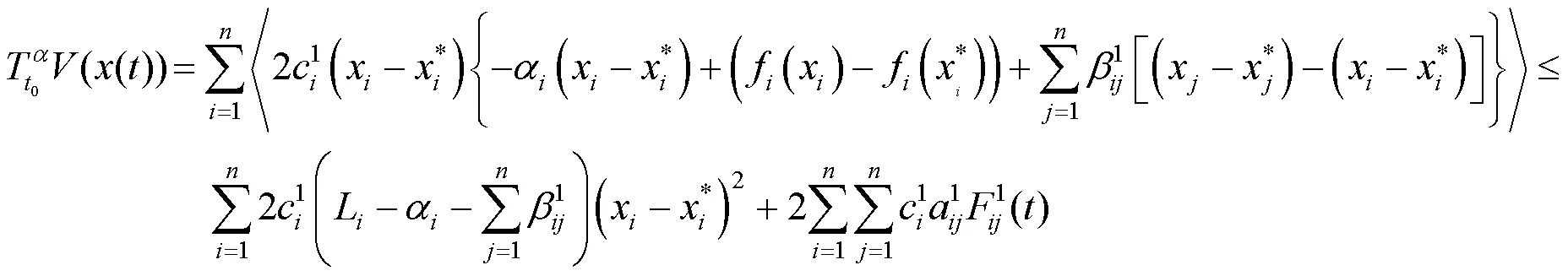
利用條件（1）～（2）和文獻[9]的引理2.4，有

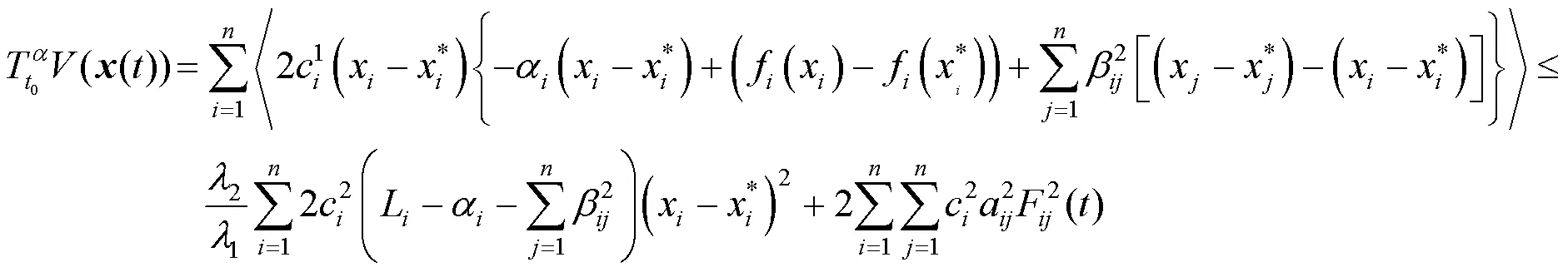
3　實例

例 設有適型分數階系統

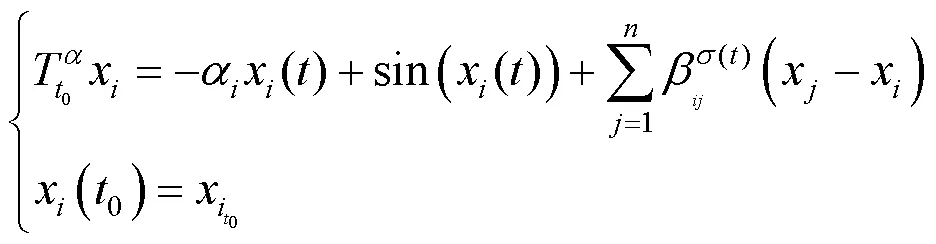
4　結語

[1] 嚴燁．分數階微分系統穩定性及其應用的研究[D]．上海：東華大學，2012．

[2] 張鳳榮. 分數階微分系統的穩定性分析[D]．上海：上海大學，2012.

[3] 孫軼男，徐曉明，馮立婷．Caputo型分數階導數的一個離散格式[J]．科學技術創新，2020（18）：152-153.

[4] 梁家輝．Caputo分數階導數的一些性質[J]．數學的實踐與認識，2021，51（9）：256-269.

[5] Khalil R，Al Horani M，Yousef A，et al．A new definition of fractional derivative[J]．J Comput Appl Math，2014（264）：65-70.

[6] Abdeljawad T．On conformable fractional calculus[J]．J Comput Appl Math，2015（279）：57-66．

[7] Benkhettou N，Hassani S，Torres D F M．A conformable fractional calculus on arbitrary time scales[J]．J King Saud Univ Sci，2016，28：3-98．

[8] Abdourazek S，Abdellatif B M，Ali H M，et al．Stability analysis of conformable fractional-order nonlinear systems[J]．Indagationes Mathematicae，2017，28：1265-1274．

[9] Li H L，Jiang Y L，Wang Z L，et al．Globlal Mittag-Leffler stability of coupled system of fractional-order differential equations on network[J]．Applied Mathematics and Computation，2015，270： 269-277．

[10] Li H L，Hu C，Jiang Y L，et al． Global Mittag-Leffler stability for a coupled system of fractional-order differential equations on network with feedback controls[J]．Neurocomputing，2016，214：233-241．

[11] Luo R Z，Su H P．The stability of impulsive incommensurate fractional order chaotic systems with Caputo derivative[J]．Chinese Journal of Physics，2018，56：1599-1608．

[12] Zahariev A，Kiskinov H，Angelova E．Linear fractional system of incommensurate type with distributed delay bounded Lebesgue measurable initial condition[J]．Dynamic Systems and Applications，2019，28（2）：491-506．

[13] Lekdee N，Sirisubtawee S，Koonprasert S．Bifurcations in a delayed fractional model of glucose-insulin interaction with income-

mensurate orders[J]．Advances in Difference Equations，2019，318：1-22．

[14] Li Y，Chen Y Q，Podlubny I．Stability of fractional-order nonlinear dynamic systems：Lyapunov direct method and generalized Mittag-Leffler stability[J]．Computers & Mathematics with Applications，2010，59（5）：1810-1821．

The stability for one class of the conformable fractional order coupled nonlinear system on switched network

GAO Yang1，PANG Qiyue2

（1. School of Mathematics，Daqing Normal University，Daqing 163712，China；2. School of Mathematics and Statistical，Northeast Petroleum University，Daqing 163711，China）

Caputo derivative；conformable fractional order derivative；fractional exponential stability；Mittag-Leffler type stability

1007-9831（2022）04-0001-05

O175.6

A

10.3969/j.issn.1007-9831.2022.04.001

2021-10-23

黑龍江省自然科學基金項目（HL2020A017）

高揚（1979-），男，黑龍江大慶人，教授，博士，從事非線性系統研究．E-mail：gy19790607@163.com