基于小波變換模極大值法的涂層信號奇異性檢測

杜晶晶 張軍芳 劉建曉 殷春英 杜鵬

摘? 要：熱噴涂涂層厚度多在微米量級，超聲檢測過程中由于涂層很薄，其上、下界面反射回波將產生疊加與干涉，超聲信號波形發生畸變。針對涂層超聲信號的奇異性檢測問題，該文采用小波變換模極大值法對低碳鋼表面上噴涂的鋁涂層的超聲信號進行奇異性檢測，進而測量涂層厚度。實驗分析證明，超聲測量的鋁涂層厚度值與金相測量值基本符合。

關鍵詞：超聲檢測? ?涂層? ?小波變換模極大值? 信號奇異性

中圖分類號：O47? ?文獻標識碼：A? ?文章編號：1672-3791（2022）03（a）-0000-00

Singularity Detection of Coating Signal Based on Wavelet Transform Mode Maximum Method

DU JingjingZHANG Junfang LIU Jianxiao YIN Chunying DU Peng

（Department of Physics and Electronic Information Hengshui University，Hengshui， Hebei Province，053000 China）

Abstract： The thickness of thermal spraying coating is mainly in the order of micron. In the ultrasonic testing process， because the coating is very thin， the reflection echo of the upper and lower interfaces will produce superposition and interference， and the ultrasonic signal waveform will be distorted. In order to detect the singularity of ultrasonic signal of coating， the wavelet transform mode maximum method is used to detect the singularity of ultrasonic signal of aluminum coating sprayed on the surface of low carbon steel， and then measure the thickness of coating. The results show that the thickness of aluminum coating measured by ultrasonic is consistent with that measured by metallography.

Key Words： Ultrasonic testing; Coating;Modulus maxima of wavelet transform;Signal singularity

目前，熱噴涂技術已在醫療器械、核工業、船舶制造業以及航空航天等諸多領域中得到了廣泛應用，而熱噴涂零件中的涂層厚度測量也開始成為當今工業領域的重點研究內容[1]。通常，熱噴涂層的厚度屬于微米級別，這對于其厚度的無損檢測具有重要價值，其中利用涂層上、下表面回波信號聲程差和涂層材料的聲速來獲取涂層的厚度是最簡單直觀的一種方法[2]。對于薄涂層而言，在超聲波的傳輸過程中，其上下界面上的回波會有疊加干涉產生，波形畸變，進而無法直接在時域內對其界面回波所達到時的具體位置進行直接識別。在這樣的情況下，不僅需要找尋一種有效的表征，同時也需要找到一種方法來進行涂層中奇異性超聲信號的處理。

關于涂層中具有奇異性的信號檢測，國內外的相關研究比較多。在這些研究中，通常都借助于頻譜分析技術中的傅里葉變換對信號中的奇異點進行歸一化處理。通過研究可知，傳統形式的傅里葉變換并不能敏銳感知到信號中的奇異性，而在小波分析理論中，可對小波變換模具體的極大值曲線進行跟蹤，以此來檢測奇異點在信號中所處的具體位置。目前，小波變換已經在對信號進行奇異性檢測的過程中得以廣泛應用[3]。基于對超聲無損測厚原理及小波分析方法的研究，該文將采用小波變換模極大值法檢測涂層的超聲信號奇異點，并計算得到低碳鋼表面的鋁涂層厚度驗證該方法的有效性。

1小波變換

超聲信號并不平穩，在對變異信號處理過程中僅可以通過時域以及頻域來進行分析。小波變換是近年來一種新興的分析方法，其應用基礎是傅里葉變換。該方法突破了傳統傅氏變換中不具備分辨力的時域限制，可分析特定時段、頻帶中的信號，對頻域以及時域的局部化性分析良好。同時，因其頻率方面所應用的時域取樣步長屬于逐漸精細形式，可對信號中的任何一個細節進行聚焦。經小波變換后信號中的奇異性將會在很多尺度上呈現出瞬態或是突變特性，這使得小波變換方法具有很好的應用意義，且發展潛力也十分顯著。

檢測突發信號的連續可微的小波基在小波變換處理中具有關鍵作用。其中的墨西哥帽小波是高斯函數的標準二階導數，在地球物理學上常被稱為Ricker小波，在該領域經常被用于地震數據建模[4]。Mexihat小波滿足小波允許條件;在時域和頻域具有很好的局部化[5];屬于連續性低通平滑形式函數的導數，在應力波中奇異性檢測方面的優勢十分顯著;具備對稱性及二階消失矩，在應力波脈沖形應變檢測方面十分適用。基于此，該文選取墨西哥帽小波對涂層奇異性信號進行檢測。

2奇異性檢測

連續小波變換以信號頻率具有的自適應能力作為依據，對時間窗進行合理選擇，在對由于瞬時變化出現的高頻信號信息進行分析時，小波變換可對細節信息實現更好地觀察。對f（t） L2（R），其連續小波變換定義為? [5]。

定義 和 的小波變換： ， 。

設 ，對一實函數f（t）有如下形式的小波變換：

式中 和 分別與通過 進行光滑處理后的函數一階和二階導數成正比，一階導數的極值點和二階導數的零點相對應，且為這一函數拐點;同時一階函數最大絕對值與突變點相對應。基于此， 幅值極大絕對值點與f（t）函數中的突變點相對應， 函數的零點與 函數的拐點具有一致性。

假設 是由f（t）經小波變換得來的函數，在a0這一特定尺度上，對f（t）這一函數做小波變換，便可獲得其連續變換系數，記作Wf （a0，b），在某特定領域中，若b0中任意一點b都能和 相符，我們便將（a0，b0）點叫作極大值點，屬于小波變換系數所具有的模極大值[6]。

3 試驗與驗證分析

該次試驗中，選取的試樣是在鋼基板上通過熱噴涂技術制備出的涂層，該涂層屬于純鋁涂層，其厚度在180～200μm之間，在通過光學顯微鏡進行觀測時，獲得到的顯微金相形貌如圖1所示，其中的序號1和序號2是采樣點，序號1的采樣值是218μm，序號2的采樣值是270μm。該試驗通過接觸式超聲縱波脈沖回波技術來進行鋁涂層中的超聲信號檢測，以此來發現其奇異性，檢測中主要參數如下：（1）所選探頭為接觸式縱波單晶片平探頭，其型號是10C6N;（2）所選晶片材料為鈷鈦酸鉛形式的陶瓷，其中心頻率f的取值是10MHz，晶片直徑d的取值是6mm。

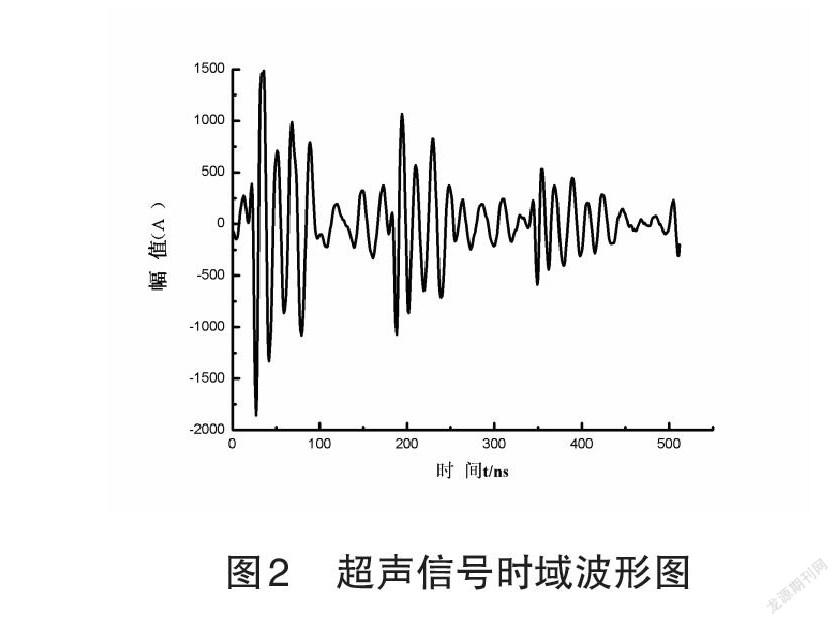
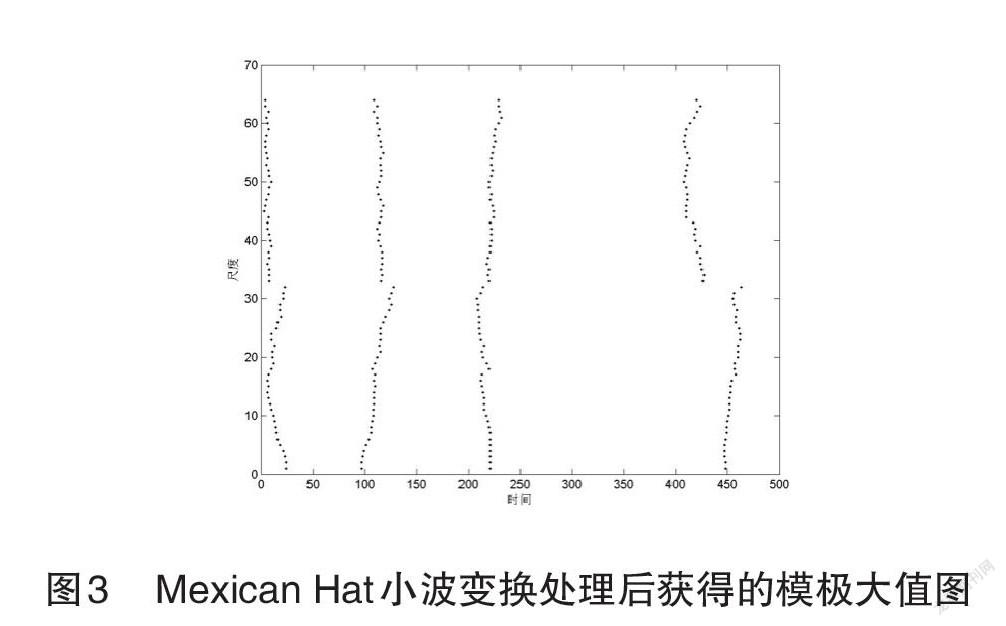
圖2是經超聲檢測在該鋁涂層中獲取到的信號時域波形（以采樣點2為例）。在該薄涂層內，超聲波在傳播過程中將會在兩個界面上出現反射回波疊加現象，其中的一個界面在耦合劑與鋁涂層之間，另一個界面在鋁涂層和基體之間，圖2中用橢圓標記出的位置便是回波疊加產生的位置，在該位置上，波形會出現突變現象，無法在時域內直接對這兩個界面上回波產生的具體位置直接進行判斷。基于此，該次通過Matlab軟件來進行時域內原始信號的連續小波變換，并對其模極大值進行獲取，圖3就是以采樣點2為例，通過Mexican Hat小波進行小波變換處理之后所獲得的模極大值圖。

對于與小波系數中的極大值點具有對應關系的信號奇異點，如果在某一刻信號出現了奇異，經小波系數處理之后獲得的模極大值圖上的模極大值連線就會反映出很大尺度范圍的變化。因信號發生奇異的位置處于這個較大的尺度范圍中，所以這一范圍里的所有小波系數都會獲得到相應的模極大值，且這些模極大值也具有最大的處理能量。為實現單一尺度情況下奇異點所處時刻誤差的有效降低，該次研究中，特對每一個尺度上每個時間點上的模極大值都進行了平均值獲取，這些平均值所具有的幅值將會反映出每一個時間點內的能量值和信號所具有的奇異程度。圖4是這一試樣中的兩個采樣點經小波變換之后獲得的平均極大值幅值圖。

觀察圖4（a）、（b），兩 位置上的小波系數平均極大值已經達到了最高值，具有最大的能量，因此也具有最大的奇異性;在兩 位置上，其平均模極大值已經超出了附近的平均模極大值能量，其信號所具有的奇異性也比較大。通過小波變換模極大值方法的信號奇異性檢測原理可知， 所對應的是回波達到了耦合劑與鋁涂層之間界面的時刻; 所對應的是回波達到鋁涂層與低碳鋼之間界面的時刻。而回波到達這兩個界面的時間點差值就是鋁涂層內超聲波往返一次所需的時間。依超聲測厚公式 ，經查超聲波在鋁涂層中的傳播速率為6375m/s，計算可得兩采樣點的厚度值分別為226μm、261μm。相比較光學顯微鏡所測量到的涂層厚度（218μm、270μm）而言，其計算誤差符合要求，可用來進行薄涂層厚度的無損檢測。表1是鋁涂層試樣厚度的計算精度。

4 結語

在薄層介質內，超聲波的傳播會在多層界面位置出現反射回波疊加現象，進而導致波形突變，而通過小波變換模極大值的方法來進行信號奇異點檢測則十分有效。該次主要對Mexican Hat以及Sym4這兩種小波進行了特性比對，并進行了相應的驗證分析，經分析發現，前者在薄涂層中的信號異常檢測中更加適用，可對厚度范圍在180～200μm之間的純鋁薄涂層厚度進行檢測，相比較金相檢測而言，該方法具有更小的計算誤差。由此可見，該方法在薄涂層厚度無損檢測中具有非常好的適用性和可行性。

參考文獻

[1] 王勝新.基于超聲的多層異質薄膜材料厚度檢測方法研究[D].成都：電子科技大學，2017.

[2] 羅文，張偉，赫麗華，等.碳纖維復合材料表面雷達吸波涂層超聲測厚方法研究[J].失效分析與預防，2021，16（4）：233-237.

[3] 鄭茜.基于插值小波的信號奇異性檢測和圖像邊緣提取[D].成都：電子科技大學，2018.

[4] 高曉旸，嚴如強.小波變換理論及其在制造業中的應用[M].姚福來，譯.北京：機械工業出版社，2019：32-33.

[5] 孫延奎.小波變換與圖像、圖形處理技術[M].2版.北京：清華大學出版社，2018：136-138.

[6] 宋穎，施文杰，孫寶臣.基于自適應連續小波模極大值算法的車輪擦傷定量評估[J].振動與沖擊，2021，40（12）：168-178，209.