改進蝙蝠算法在紙病圖像增強中的應用

毛艷玲，李天宇，吳 浩，陳明舉

（1. 四川輕化工大學自動化與信息工程學院，四川 宜賓 644000；2.人工智能四川省重點實驗室，四川 宜賓 644000）

引 言

隨著紙機車速的提升、紙幅寬度的加大，造紙過程中紙張出現缺陷的幾率增大[1]。因此，在造紙過程中及時發現有病害的紙張是我國造紙工業技術自主研發的重要方向之一。紙病檢測系統可以提前發現紙張缺陷，以便及時去除缺陷紙張[2]。紙病檢測系統的圖像采集模塊主要由一個或多個線性CCD（Charge Coupled Device，電荷耦合器件）相機組成，利用CCD 技術對產品表面質量進行檢測具有結構簡單、性能穩定可靠等優點[3-4]。但是基于CCD技術的紙張檢測系統也具有以下缺點[5]：（1）被測紙張的反光性影響CCD接收的像素的RGB值，造成象圖的邊界模糊；（2）若CCD 成像的對比度較差，則會使得圖像暗區灰度層次增加，不利于圖像和背景的分離；（3）檢測過程中沿光軸方向振動使被測件輪廓在CCD 成像的清晰度發生變化。因此，研究紙病圖像增強算法具有重要意義。

傳統的紙病圖像增強方法包括空域增強、頻域增強和混合域增強[6-7]。除此之外，李光明等[8]提出了基于多尺度形態學梯度的圖像增強方法，曲蘊慧等[9]提出了利用Gabor 濾波器和Gussian 濾波器去除紙張的紋理干擾。馮波等[10]將模糊邏輯理論應用在紙病檢測中，具有很好的檢測效果。但上述方法存在計算量大、參數手動設置、效率低和適應性差的缺點。基于啟發式算法的圖像增強方法是一種新穎的圖像增強技術，圖像增強被認為是一個優化問題，利用各種基于啟發式的群體智能優化算法可以更高效、適應性更強地解決這些優化問題[11]。蝙蝠算法是基于蝙蝠種群捕獵過程的回聲定位行為的隨機全局優化技術，它是處理各種優化問題的最新和最強有力的方法之一[12]，其應用主要有組合優化[13]、數據挖掘[14]、圖像處理[15-17]等。馬雙娜[15]將頻移效應和模擬退火權重引入蝙蝠算法，解決圖像多閾值分割問題。文獻[16]采用二進制蝙蝠算法對白細胞（White Blood Cells,WBCs）進行分類，結果表明優化蝙蝠算法能夠快速分類，且具有較高的準確性。文獻[17]將遺傳算法引入蝙蝠算法來對遙感圖像進行分類，實現了分類精度的提升。然而標準蝙蝠算法的搜索能力完全由隨機漫步決定，并且由于標準蝙蝠算法隨機漫步執行條件的限制，導致蝙蝠種群多樣性在迭代過程中驟減，種群容易陷入局部最優，因此算法后期存在收斂速度緩慢，甚至“早熟”的問題。

紙病圖像存在照度不均、清晰度低、部分紙病細小且對比度低，如果直接采用蝙蝠算法，無法較好地實現對紙病圖像的增強。基于上述分析與啟發，將混沌映射與引力搜索引入到蝙蝠算法中，提出一種基于混沌映射和引力搜索優化的圖像增強蝙蝠算法，利用混沌映射更新響度和脈沖發射率，提高蝙蝠種群解的多樣性；采用引力搜索算法更新蝙蝠個體速度，提高蝙蝠算法的搜索能力，將改進的蝙蝠算法自適應搜索最佳伽馬值，對紙病圖像進行伽馬變換，以解決標準蝙蝠算法易出現早熟現象和收斂速度慢等問題，并提高低照度條件下紙病圖像的對比度。

1 理論基礎

1.1 蝙蝠算法

蝙蝠算法就是對每個蝙蝠個體的頻率、速度、脈沖發射率和響度迭代更新來獲得最優解[18]。蝙蝠種群的頻率、速度和波長更新方式如式（1）～（3）所示。

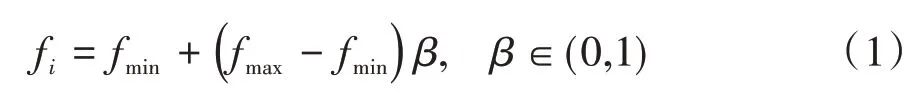
其中：β為一個隨機變量，fmin為蝙蝠發出的最低頻率；fmax為蝙蝠發出的最高頻率；fi表示第i只蝙蝠發出的頻率，其中fi∈[fmin,fmax]。

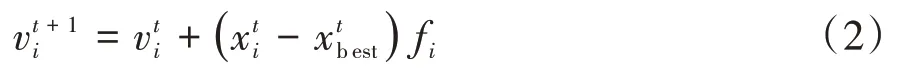
其中：表示蝙蝠i在第(t+ 1 )次迭代時的位置，若在當前解中產生了一個最優解，則以隨機游走方式生成新的局部解：

其中：xnew為新的局部解，xold為當前局部最優解，ε為一個隨機數且ε∈[-1,1]，At為蝙蝠群體在同一代中的平均響度。

蝙蝠在尋找獵物的過程中，隨著搜索范圍的縮小，蝙蝠個體響度逐漸減小直至不再變化，脈沖發射率不斷增加，以動態掌握目標獵物的方位。第i只蝙蝠的聲波響度和脈沖發射率使用式（5）和（6）更新。

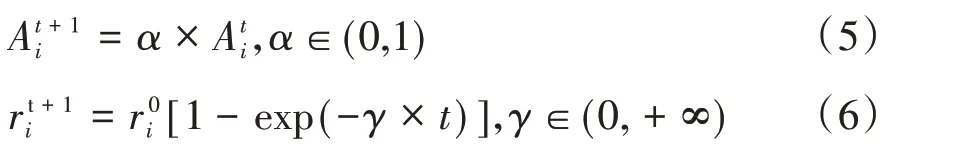
在式（4）中只有當滿足“rand＞ri”的條件下隨機漫步才被執行，其中rand為0～1 之間的隨機數。隨著迭代次數的增加，由式（6）可知，逐漸增大，因此隨機漫步的幾率逐漸減小，種群生成多樣性解的概率減小，種群容易陷入局部最優導致早熟收斂。同時，式（2）和式（3）表明標準蝙蝠算法的速度和位置更新僅涉及到對當前最優蝙蝠的學習，因此，一旦當前最優個體被局部極值吸引，標準蝙蝠算法本身并沒有有效的變異機制來使其“跳出”局部極值，種群多樣性將迅速喪失進而失去進化能力，若個體陷入局部最優，將會影響算法的收斂速度。因此，將混沌映射與引力搜索引入到蝙蝠算法中，提高紙病圖像的增強能力、檢索搜索時間。

1.2 混沌映射

對于大部分的具有隨機成分的元啟發式算法，算法的隨機性是通過使用概率分布來實現的[19]。混沌是一種具有隨機性的運動狀態，它能夠在一定范圍內按自身“規律”不重復地遍歷所有狀態[20]。近年來，許多優化算法通過使用混沌映射替換原始算法的隨機參數或變量而提高了算法的性能。利用混沌不可重復性、遍歷性和混合特性的優點，基于混沌映射的算法具有更好的全局搜索能力[21]，同時基于混沌映射的算法可能比標準概率分布的標準隨機搜索具有更高的執行速度。其中正弦圖是替代蝙蝠算法中響度或脈沖發射率的最合適的混沌圖[19],因此本文改進蝙蝠算法采用正弦映射來更新蝙蝠個體的響度和脈沖發射率，如式（7）所示：

其中：Xk為蝙蝠個體的響度或脈沖發射率；a為控制參數，取值為2.3。

1.3 萬有引力搜索算法

萬有引力搜索算法是模擬物理學中萬有引力和牛頓定律的種群優化算法，在搜索空間中，每一個粒子都有一個慣性質量，低慣性質量粒子向高慣性質量粒子移動[22]，粒子之間相互作用的萬有引力是粒子運動的動力，當粒子移動到最優位置時，該位置即為所求問題的最優解[23]。

假設一個具有n個粒子的引力系統，并且粒子i的位置為：

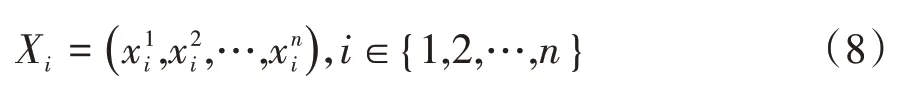
表示粒子i在維度d上的位置。根據萬有引力定律，在t時刻，d維度上，質點i從質點j處所獲得引力定義如下：

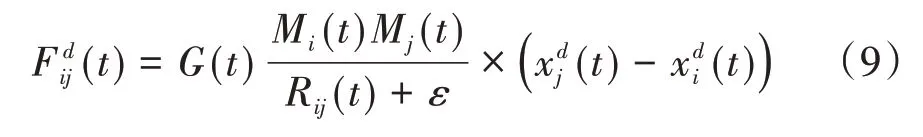
其中：t時刻的重力常數表示宇宙初始重力常數，通常設置為1，?為常數，T表示最大迭代次數；t時刻粒子i和粒子j之間的歐氏距離；Mi和Mj分別代表質點i和質點j的質量(t)與(t)分別為t時刻質點i與質點j的位置；ε是一個常數。

其中：fi(t)表示粒子i在t時刻的適應度值，fbest和fworst分別表示搜索空間中粒子的最優適應度值和最差適應度值。

根據牛頓第二定律，在t時刻，粒子i在d維上的加速度定義為：

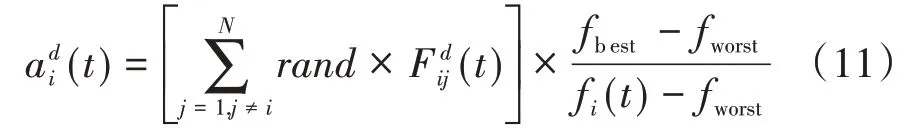
其中：粒子i所受的作用力是其他所有粒子作用力(t)的總和。

最后，對于每一次的迭代過程，粒子都按照牛頓第二定律如式（12）～（13）來更新它的速度和位置。

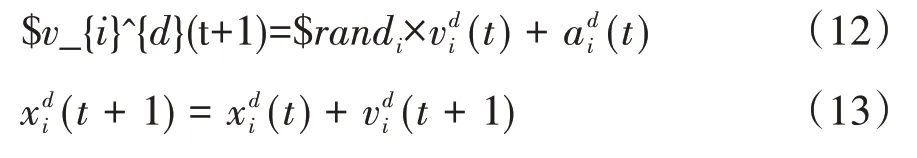
其中：randi是[0,1]區間內的隨機數。

2 基于混沌映射和引力搜索優化的紙病圖像增強蝙蝠算法

2.1 基于引力搜索和混沌映射的蝙蝠算法收斂優化

蝙蝠算法具有收斂性強和搜索范圍大的優點，但是隨著迭代次數增加，脈沖發射率ri增加，這使得后期局部隨機漫步被執行的概率大大降低[21,24]，種群解的多樣性降低，算法容易早熟收斂，同時隨著響度Ai逐漸減小，對新產生的解，算法的接納能力降低[12]。為了提高解的多樣性，使算法以更快的速度執行搜索步驟，根據文獻[25]，更新響度和脈沖發射率，即：

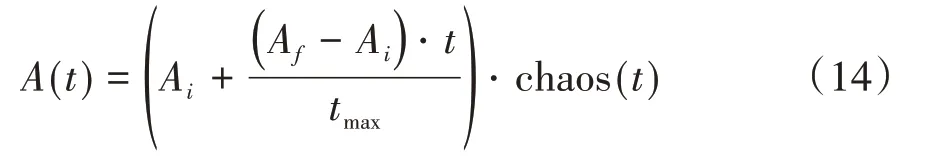
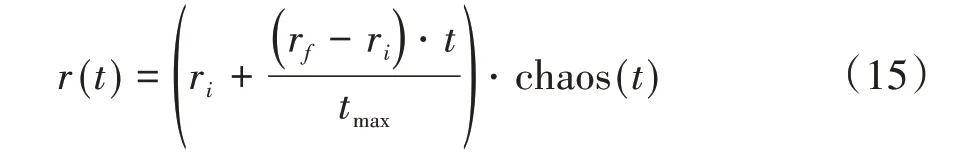
式中：Ai和Af表示線性遞減函數的初始值和最終值，ri和rf代表線性增長函數的初始值和最終值。其中，Ai= 1，Af= 0.1，ri= 0.1，rf= 0.8，chaos(t)代表典型的混沌函數，這里代表正弦圖。標準蝙蝠算法隨機漫步決定了蝙蝠算法的探索能力，由于標準蝙蝠算法本身變異機制的限制，若算法陷入局部最優，將影響算法收斂速度和性能[12]，為了解決以上問題，將蝙蝠算法與其他算法的混合是提高算法性能的最有效方法[26]，改進算法將引力搜索算法引入蝙蝠算法，粒子通過相互之間的吸引力來朝著最佳解方向移動，減少算法陷入局部最優解的可能性[23]，引力搜索算法的局部搜索能力提升了算法的探索能力，加快全局搜索的收斂速度[27]。根據萬有引力算法，本文提出粒子速度更新公式，在(t+ 1 )時刻，粒子i在維度d上的速度更新策略定義為：

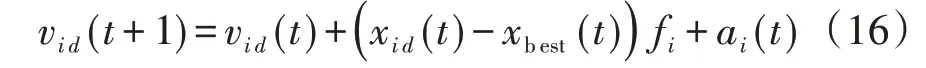
經過以上改進之后，基于混沌映射和引力搜索的蝙蝠算法的偽代碼如下：

2.2 紙病圖像蝙蝠算法

從視覺效果上來看，由對比度引起的降質圖像一般有3種情況，分別是偏亮、偏暗和灰度集中在某一區域。低對比度的紙病圖像屬于偏暗的降質圖像，根據文獻[28]，本文選擇伽馬變換來對較暗區域拉伸，改善圖像對比度。伽馬校正是一種常見的增強圖像對比度的方法，通過對過暗的圖片使用一個可變的參數γ來提升圖像暗部細節，改變圖像的亮度和對比度。伽馬校正的公式如下所示：

式中：l∈[0,lmax]，表示輸入圖像實際灰度值；T(l)表示輸出圖像實際灰度值；lmax表示輸入圖像灰度最大值；校正參數γ控制圖像拉伸程度，不同γ將產生不同的拉伸效果。對于全局伽馬校正而言有必要選擇一個最佳的γ值，以便產生更好質量的圖像。

利用改進的蝙蝠算法（圖1）確定待增強圖像所對應伽馬變換的最佳參數γ，通過伽馬變換曲線實現增強圖像的對比度，算法的具體步驟如下：

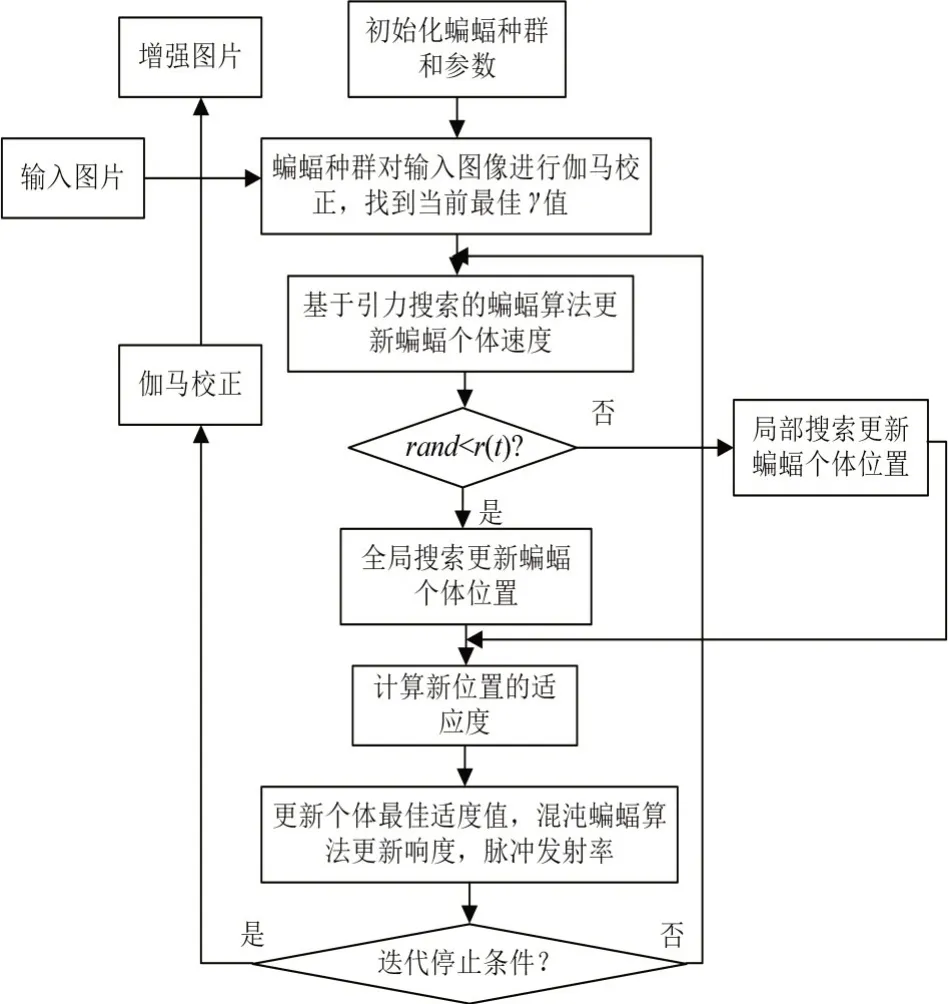
圖1 增強圖像流程圖

步驟1：輸入紙病圖像。

步驟2：初始化種群fmin和脈沖發射率ri0最大迭代次數tmax。

步驟3：對輸入的紙病圖像進行伽馬校正。每一個蝙蝠個體對圖像進行伽馬校正，通過式（17）計算每個蝙蝠個體的適度值f，種群最佳適應度值fbest、種群最差適應度值fworst，找出當前最佳γ值。

步驟4：蝙蝠個體更新。更新蝙蝠個體的頻率、位置，基于引力搜索的蝙蝠算法更新蝙蝠個體速度。

步驟5：計算當前全局最優解。若滿足判斷條件，則將新的蝙蝠個體適度值fnew作為當前個體最佳適度值，更新全局最優解和全局最差解，得出當前最佳伽馬值。

步驟6：判斷是否滿足迭代停止條件，若未達到，則返回步驟4。若滿足迭代停止條件，則退出循環。

步驟7：使用迭代中存儲下來的最優γ值增強圖像。

3 實驗結果和分析

3.1 紙病圖像增強實驗

研究對象是低照度條件下的紙病圖像，如圖2（a）、圖3（a）、圖4（a）、圖5（a）所示，它們都為低照度下黑斑缺陷的紙病圖像。從圖中可以看出，原始圖像的可觀測性比較差，對比度低，紋理細節不清晰，為滿足需求，采用上述改進算法對圖像進行處理。為了驗證本文基于改進蝙蝠算法的圖像對比度增強的效果，將基于直方圖均衡化（HE）優化的紙病圖像增強算法、基于限制對比度自適應直方圖均衡化（CLAHE）優化的紙病圖像增強算法、基于標準蝙蝠算法的紙病圖像增強算法、基于混沌蝙蝠算法的紙病圖像增強算法與本文算法分別進行比較，其中所有蝙蝠算法參數設置如下：種群大小為30，迭代次數為100，最小頻率為0，最大頻率為1。實驗結果如圖2～5所示。

圖2 紙病圖像1增強效果

圖3 紙病圖像2增強效果

從增強結果圖像中可以看出，基于傳統直方圖均衡化的算法和基于限制對比度自適應直方圖均衡化的算法過度增強了圖像對比度，使得圖像有所失真，基于標準蝙蝠算法、基于混沌蝙蝠算法和本文算法都對圖像有所增強。本文算法增強效果最好，有效提高圖像對比度的同時能夠突出缺陷邊緣細節，綜合結果對比得出本文算法處理圖像能更好地呈現視覺效果。

3.2 性能比較

為了對本文提出的方法處理紙病圖像進行有效客觀評價，分別采用對比度（CON）、灰度差分乘積函數（SMD2）、均值3 種標準對實驗結果進行評估。對比度是畫面黑與白的比值，也就是從黑到白的漸變層次。比值越大，從黑到白的漸變層次就越多，從而色彩表現越豐富。對比度越大，圖像越清晰醒目，對比度小，圖像越模糊。對比度C采用式（18）計算。

灰度差分乘積聚焦評價函數以相鄰像素灰度值差表征圖像的清晰度[29]，灰度差分乘積聚焦評價函數采用式（19）計算。

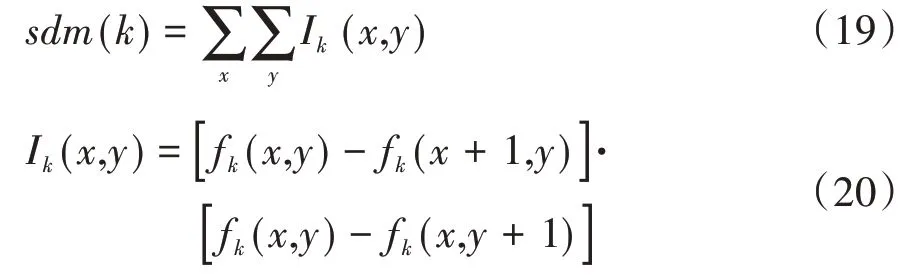
其中：Ik(x,y)是像素fk(x,y)與其左右及正下像素灰度差的乘積，然后對整幅圖像進行像素遍歷計算即可得到評價值sdm(k)。當該函數值最大時，對應圖像最清晰。

均值即圖像像素的平均值，它反映了圖像的平均亮度，平均亮度越大，圖像質量越好，均值u計算如下：

其中：F為待評價圖像，M和N為待評價圖像的大小。

用式（18）～（21）評價本文提出算法和其他算法對圖像增強的效果，結果如表1 ～3 所示。表1 ～3分別為通過對原圖和5種不同算法增強后的紙病圖像對比度、灰度方差乘積函數和均值的計算結果，以比較5 種紙病增強算法性能，其中算法1、算法2、算法3、算法4 分別為基于HE 算法優化的紙病增強算法、基于CLAHE 法的紙病增強算法、基于標準蝙蝠算法優化的紙病增強算法、基于混沌蝙蝠算法優化的紙病增強算法。由表1～3 可以得出：本文提出的紙病圖像增強算法的對比度、灰度方差乘積函數值和均值優于基于標準蝙蝠算法優化的紙病圖像增強算法和基于混沌蝙蝠算法優化的紙病圖像增強算法，增強效果最佳。雖然算法1 和算法2 兩種算法下4張圖片的3種指標較高，但是由圖2～4可知算法1 和算法2 存在過度增強現象，視覺效果較差。本文算法下4 張圖片的平均對比度相對于算法3 增加了78%，相對于算法4 增加了39.8%；平均灰度方差乘積函數值相對于算法3 增加了70.6%，相對于算法4 增加了33.4%；均值相對于算法3 增加了43.5%，相對于算法4增加了48.8%。

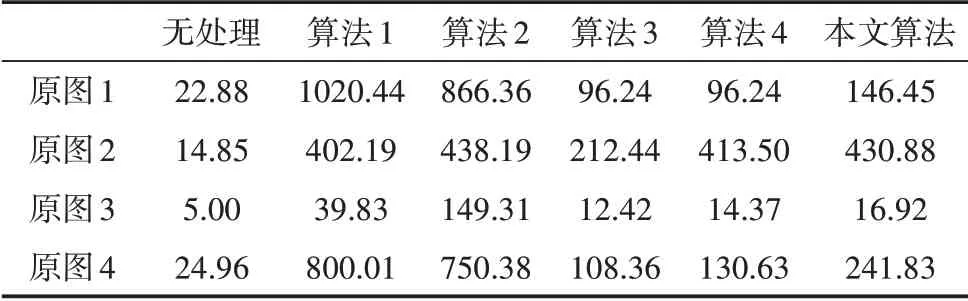
表1 對比度指標比較

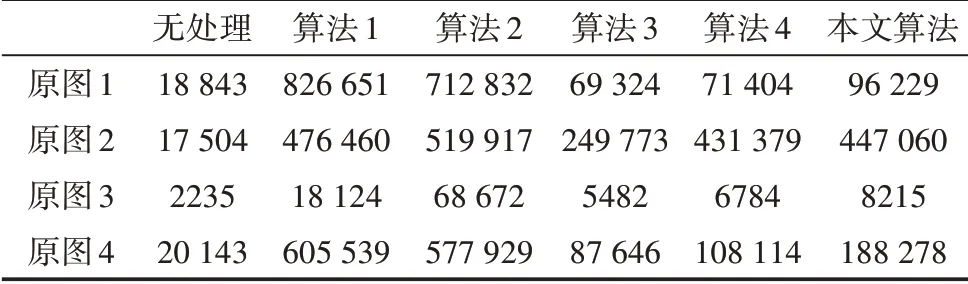
表2 灰度差分乘積函數指標比較

表3 均值指標比較

4 結束語

為了解決低對比度、低照度紙病圖像視覺效果不佳、邊緣模糊等問題，在蝙蝠算法基礎上進行改進，提出了一種基于改進的蝙蝠算法的紙病圖像增強方法。通過在標準蝙蝠算法中引入混沌映射和引力搜索算法分別更新個體響度、脈沖發射率和個體速度增強種群多樣性，平衡了算法的局部和全局搜索能力。同時，將提出的改進蝙蝠算法搜索伽馬變換的最佳參數γ實現圖像的對比度增強。結果表明，與基于傳統直方圖均衡優化的紙病圖像增強算法、基于限制對比度自適應直方圖均衡優化的紙病增強算法、基于標準蝙蝠算法優化的紙病圖像增強算法、基于混沌蝙蝠算法優化的紙病圖像增強算法相比，本文算法的增強效果為所有對比算法中最優，其中對比度相對于標準蝙蝠算法優化的紙病圖像增強算法增加了78%，相對于混沌蝙蝠算法優化的增強算法增加了39.8%；灰度方差乘積函數值相對于標準蝙蝠算法優化的紙病圖像增強算法增加了70.6%，相對于混沌蝙蝠算法優化的增強算法增加了33.4%；均值相對于標準蝙蝠算法優化的紙病圖像增強算法增加了43.5%，相對于混沌蝙蝠算法優化的增強算法增加了48.8%。