基于智能分數階互補滑模的PMLSM直接推力控制

苗 雨，趙希梅

(沈陽工業大學 電氣工程學院，沈陽 110870)

0 引 言

永磁直線同步電機(以下簡稱PMLSM)具有效率高、推力大、響應快等優點，近年來在航空航天、數控機床、機器人設備和半導體加工制造等領域得到了廣泛應用[1-2]。直接推力控制(以下簡稱DTFC)是將旋轉電機中的直接轉矩控制延伸到直線電機上的一種控制策略[3]。DTFC直接對磁鏈和推力進行控制，與矢量控制相比結構更簡單，速度響應更快，是軌道交通和運輸領域的首選[4-5]。DTFC系統具有快速的響應和良好的魯棒性，但由于其穩態誤差和超調量較大，無法使系統的跟蹤精度滿足高性能要求[6]。因此，設計一種既可以保留DTFC快速響應的優點，又具有較小速度和推力脈動的控制器，使系統獲得更好的跟蹤性能，對實現PMLSM的高精度高速度控制具有重要意義。

近年來，國內外專家學者為提高PMLSM的控制性能，進行了大量的研究。滑模控制(以下簡稱SMC)具有廣泛的應用，但由于其控制的不連續性，存在抖振問題，通常需要與其他方法結合才能達到更好的控制效果[7]。文獻[8]提出了一種基于新型趨近律的SMC，能避免開關增益持續增大，該方法可在一定程度上削弱SMC的抖振問題，并提高DTFC系統的魯棒性能，但系統仍存在較大的推力脈動。文獻[9]設計了一種帶有分數階PIαDβ型滑模面用于永磁同步電動機調速系統，通過分數階微積分算子特有的記憶特性和遺傳特性抑制了抖振問題，但系統的動態響應能力較差。文獻[10]提出了一種基于神經網絡變階次的積分滑模控制方法，該方法具有更加快速的動態響應速度，但選用傳統的積分滑模面使系統仍存在較大的穩態誤差。文獻[11]在廣義滑模面的基礎上增加了一個互補滑模面，可以提高系統的位置跟蹤精度，并降低不確定性對系統運行的不良影響，但SMC的抖振問題仍未得到較好的解決。文獻[12]將互補滑模控制和智能控制中的迭代學習相結合，該方法能夠有效抑制不確定性對系統的影響，從而加快控制器的收斂速度，提高收斂精度。

為使DTFC系統的速度跟蹤能力得到進一步提高，本文設計了一種基于RBF神經網絡的智能分數階互補滑模控制(以下簡稱IFOCSMC)方法。首先，設計了分數階廣義滑模面和分數階互補滑模面，分數階微積分算子具有濾波特性和緩慢傳遞能量的特點，分數階互補滑模面既可以削弱SMC的抖振問題，又能夠減小DTFC的推力脈動，同時也增加了運算自由度，減小系統跟蹤誤差的同時，也有較強的抗干擾能力。其次，利用RBF神經網絡對系統受到的擾動和未建模部分進行在線逼近，進一步提高系統的動態響應能力和抗干擾能力。仿真結果表明，該方法可以有效地加快系統的響應速度，減小穩態誤差，系統速度跟蹤性能得到明顯的提高。

1 PMLSM數學模型

d-q坐標系下的PMLSM電壓方程：

(1)

式中：ud，uq，id，iq，ψd，ψq分別為d，q軸電壓、電流和和磁鏈；ωr為磁鏈矢量的角速度；Rs為動子電阻。

磁鏈矢量的角速度：

(2)

式中：p為極對數；τ為極距；v為動子機械速度。

磁鏈方程：

(3)

式中：Ld，Lq為d，q軸電感；ψf為永磁體磁鏈。

磁路對稱時Ls=Ld=Lq，PMLSM的電磁推力表達式：

(4)

式中：Fe為電磁推力；ψs為定子磁鏈；δ為ψs和ψf的夾角；kf為電磁推力系數。

機械運動方程：

(5)

式中：M為動子質量；B為粘滯摩擦系數；F為系統所受擾動的負載力。

2 基于IFOCSMC的DTFC系統

PMLSM的DTFC系統結構框圖如圖1所示。

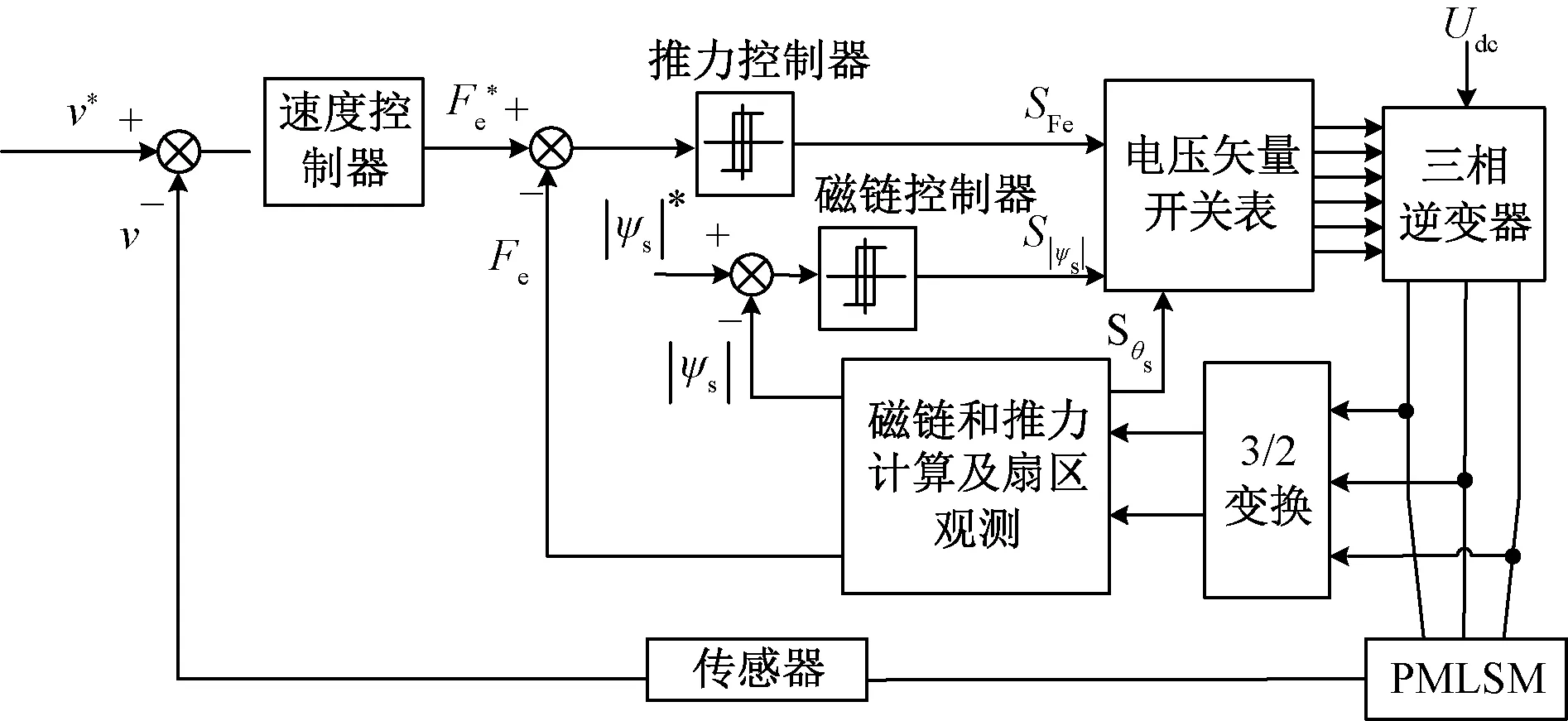
圖1 PMLSM的DTFC系統框圖

2.1 分數階微積分

(6)

式中：a和t是積分算子的上下限；α為微分算子的階次；R(α)是α的實部。當不涉及上下限問題時可簡寫為Dα。

RL型分數階微積分定義：

(7)

式中：n取整數，且m-1<αa,Γ(z)為Gamma函數。

由于分數階微積分的值無法得到精確數值解，故采用Oustaloup濾波器來逼近。設(wb,wh)為選定的擬合頻率段，該濾波器的傳遞函數：

(8)

該濾波器的零極點和增益求解公式：

wk=wbwu(2k-1+α)/n

(9)

w′k=wbwu(2k-1-α)/n

(10)

K=whα

(11)

為提高濾波器在wh和wb邊界附近的擬合效果，引入改進的Oustaloup濾波器：

(12)

式中：wk≈(bwh/d)(α+2k)/(2n+1)，w′k≈(dwh/b)(α-2k)/(2n+1)，加權參數b=10，d=9。

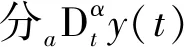
2.2 FOCSMC設計

當不考慮擾動即F=0時，電機的理想運動方程可改寫：

(13)

式中：An=-B/M，Bn=Kf/M，u為控制器輸出。

電機在實際運行時會受到不確定性的干擾，當考慮擾動即F≠0時，電機運動方程可改寫：

Anv+Bnu+H

(14)

H=ΔAv+ΔBu+(Cn+ΔC)F

(15)

式中：Cn=-1/M；ΔA,ΔB和ΔC為M和B引起的擾動變化量；H為總擾動，H未知但有界。

互補滑模控制(以下簡稱CSMC)具有較強的魯棒性，并且增加的互補滑模面能使系統具有更高的跟蹤精度，分數階互補滑模控制(以下簡稱FOCSMC)是在CSMC的基礎上，將兩個滑模面中的整數階微積分替換為分數階微積分，削弱抖振問題、減小推力脈動的同時，增加了運算自由度，能夠進一步提高PMLSM控制系統的速度跟蹤能力。

定義速度跟蹤誤差：

e=v*-v

(16)

式中：e為速度跟蹤誤差；v*和v分別為給定速度輸入和實際速度輸出。

FOCSMC的滑模面定義：

S=S1+S2

(17)

S1=Dαe+2λe+λ2D-αe

(18)

S2=Dαe-λ2D-αe

(19)

式中：Dα為分數階微積分算子；α和λ都為正常數。

分別對式(18)和式(19)兩邊求取α階導數，可得：

DαS1=D2αe+2λDαe+λ2e

(20)

DαS2=D2αe-λ2e

(21)

結合式(17)～式(19)可得：

S=S1+S2=2(Dαe+λe)

(22)

將式(22)與式(20)和式(21)聯立可確定S1和S2的關系：

DαS1-DαS2=2λ(Dαe+λe)=λS

(23)

定義Lyapunov函數：

(24)

引理1：設x(t)∈Rn是一個可微函數的向量，對于t≥t0的任意時刻，以下關系成立[13]：

(25)

結合引理1和式(18)～式(21)，求取式(24)的α階導數可得:

DαV1≤S1DαS1+S2DαS2≤

S1DαS1+S2(DαS1-λS)=

S1DαS1+S2(DαS1-λS1-λS2)=

(S1+S2)(DαS1-λS2)=

S(D2αe+2λDαe+λ2e-λS2)=

2λDαe+λ2e-λS2]

(26)

FOCSMC的控制律u由等效控制ueq和切換控制usw兩部分構成，FOCSMC的控制律表示：

u=ueq+usw

(27)

兩部分分別設計：

λ2D1-2αe+λD1-2αS1)=

(28)

(29)

式中：sat(·)為飽和函數；Φ>0為邊界層厚度，具體表示：

(30)

由于傳統的符號函數具有不連續控制的特性，故將符號函數替換為近似連續控制的飽和函數，可使SMC的抖振得到進一步削弱。將式(27)、式(28)和式(25)代入式(22)中，可以得到：

(31)

由式(31)可得該控制器滿足Lyapunov穩定性定理。

2.3 IFOCSMC設計

系統運行時，干擾會對跟蹤性能有不良影響。利用RBF神經網絡在線逼近系統受到的擾動，對系統未建模部分進行補償，進一步提高系統的控制性能。RBF神經網絡結構簡單，逼近能力強，可以避免局部最優的問題，并且具有較快的訓練速度，結構如圖2所示。

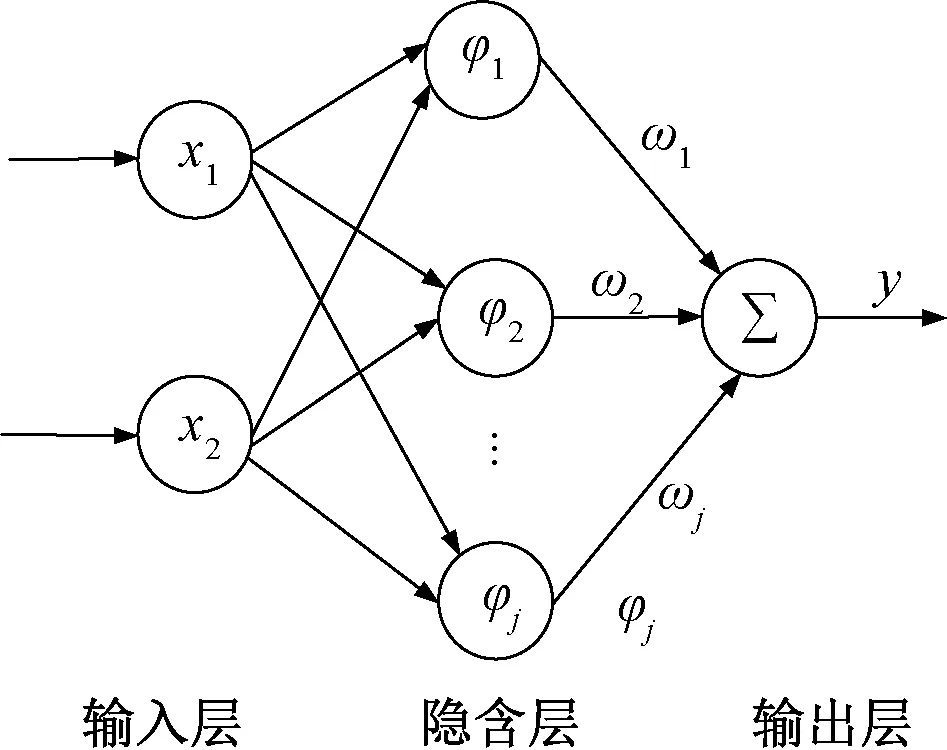
圖2 RBF神經網絡結構圖

神經網絡的輸入為速度誤差和誤差的變化率，表示：

(32)

神經網絡的激活函數為高斯函數，定義：

(33)

式中：ci為隱含層第i個節點函數的中心，σi為第i個隱含層節點函數的基寬參數。

神經網絡的輸出為每個隱含層神經元的輸出值與對應的連接權重的加權之和，表示：

(34)

式中：n為隱含層節點的數量；ωi為連接權值。

定義RBF神經網絡的輸出：

uR=WTφ

(35)

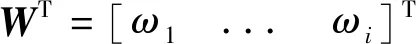
神經網絡權重調整的自適應律：

W=-η(S1+S2)φ

(36)

式中:η為神經網絡權重自適應系數。

RBF神經網絡的輸出存在一個理想的最優值：

uR*=W*Tφ+ε

(37)

IFOCSMC的結構如圖3所示。系統總控制律可寫成：

u=ueq+usw+uR

(38)

定義Lyapunov函數：

(39)

結合式(36)和式(38)可得：

(40)

由式(40)可得，IFOCSMC方法滿足Lyapunov穩定性判據。

圖3 IFOCSMC原理框圖

3 仿真結果分析

為了證明本文方法的有效性,對基于IFOCSMC的PMLSM DTFC系統進行仿真分析，并與使用CSMC和FOCSMC的系統仿真運行結果進行對比。選用的PMLSM參數:M=16.4 kg，τ=32 mm，Rs=2.1 Ω，ψf=0.09 Wb，B=8.0 N·s/m，p=3，Ld=Lq=27 mH。IFOCSMC的參數：ρ=12，η=0.5，α=0.24，λ=95，Φ=0.002，CSMC和FOCSMC的參數與IFOCSMC一致。

電機空載起動，在0時輸入幅值±600 mm/s的1.2 Hz方波信號作為速度給定信號，并在電機動子上施加如圖4所示的非周期性變化擾動。圖5為三種方法的速度響應曲線。從圖5可以看出，采用CSMC方法時，當輸入速度指令后，系統首次到達給定速度并穩定運行的時間約為0.08 s，速度超調較大，約為給定速度的6.8%，在1.3 s動子受到較大的負載擾動時，穩定運行速度有52 mm/s的下降，整體速度曲線存在明顯抖振，并且在負載增大時抖振問題更加嚴重。采用FOCSMC方法時，系統開始穩定運行的時間約為0.06 s，超調量和抖振都有明顯減小，受到負載擾動時，運行速度下降18 mm/s。采用IFOCSMC方法時，系統開始穩定運行的時間約為0.03 s，基本無超調和抖振，并且當動子受到負載擾動時速度曲線基本無波動。

圖4 非周期性擾動曲線

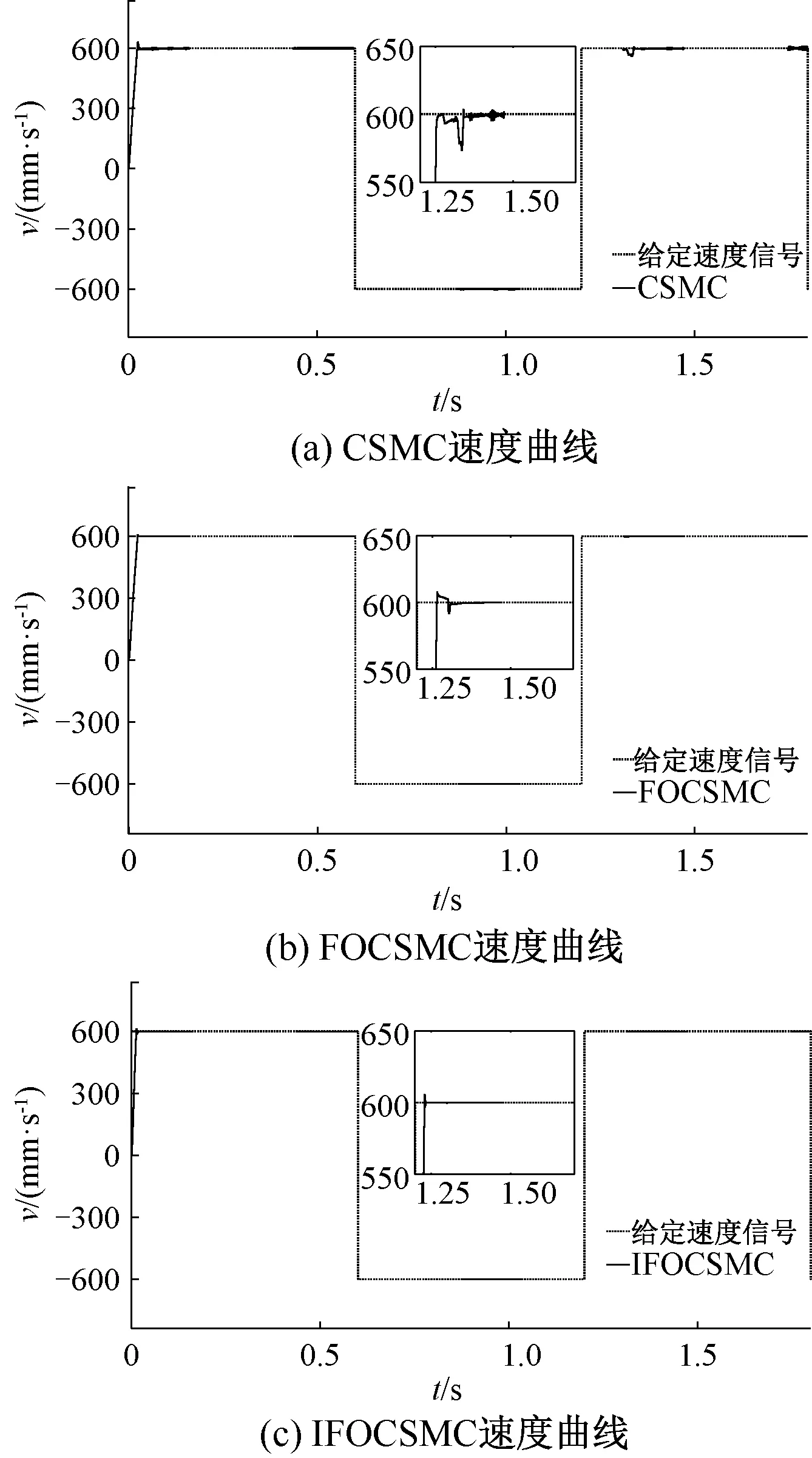
圖5 三種方法的系統速度響應曲線

圖6為三種方法的速度誤差曲線。從圖6可以看出，當電機穩定運行時，CSMC方法的系統速度跟蹤誤差范圍為-4 mm/s～11.8 mm/s，約為給定速度的1.3%。FOCSMC方法的誤差范圍為-1.8 mm/s～5.6 mm/s，約為給定速度的0.6%。IFOCSMC方法的誤差范圍為-1.2 mm/s～2.4 mm/s，約為給定速度的0.3%，與前兩種方法相比有明顯減小。對比速度跟蹤誤差曲線可知，當穩定運行時，IFOCSMC方法速度跟蹤誤差更小并且控制更加平滑。

圖6 三種方法的系統速度跟蹤誤差曲線

圖7為三種方法的電磁推力曲線。從圖7可以看出，在給定速度指令突變時，IFOCSMC方法的瞬間最大電磁推力較CSMC方法和FOCSMC方法相比有明顯增大，更大的電磁推力可使系統迅速作出響應，到達穩態后IFOCSMC方法的推力脈動也較小。

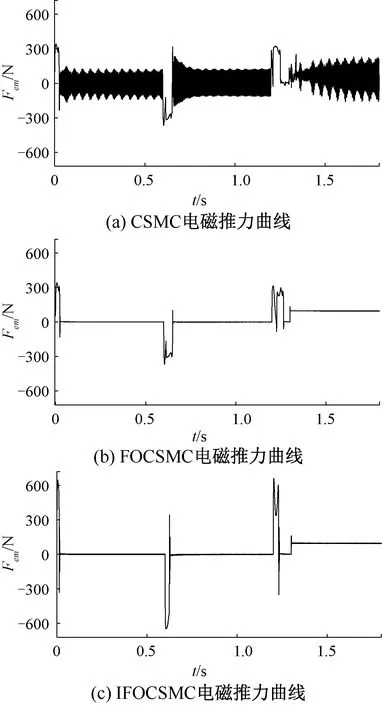
圖7 三種方法的系統電磁推力曲線

圖8為兩種方法第一次到達穩態時滑模函數的軌跡。與FOCSMC方法對比可以看出，IFOCSMC方法的滑模曲線能夠提前約0.03 s收斂到穩態，說明該方法能夠加快系統的跟蹤速度。

圖8 兩種方法的滑模收斂曲線

通過上述仿真運行結果的對比可以看出，IFOCSMC方法能夠有效抑制抖振，減小推力脈動，使系統在抗干擾能力和速度跟蹤性能上都更為出色。

4 結 語

為提高PMLSM的DTFC系統的速度跟蹤能力，本文設計了一種基于RBF神經網絡的IFOCSMC方法。該方法利用分數階互補滑模面削弱抖振并抑制推力脈動，減小了系統的穩態誤差。利用RBF神經網絡對擾動進行補償，進一步加快了系統的跟蹤速度并提高抗干擾能力。仿真結果表明，該方法能使系統具有更快的動態響應速度、更小的穩態誤差，系統的抗干擾能力和速度跟蹤能力得到了明顯的提高。