基于近似法的LED光源壽命預測

伍玉瑩，李 晟，孟慶慧，周 武，黃海松

（江西理工大學理學院，贛州 341000）

0 引言

近年來，固態照明廣泛應用于工業和生活的各個領域，發光二極管（LED）作為新一代綠色光源，以其高效率，長壽命，穩定性高，相對環境友好（它們不含汞）且功耗低等優點，開啟了照明領域的新革命。近幾年，我國LED市場規模快速擴大，2018年中國LED 照明行業市場規模達到5985 億元，2019年中國LED 照明行業市場規模達到6823 億元，年增長率達到14%，預計未來將會繼續保持高速增長。相比于傳統的照明產品，LED 照明產品具有易于智能控制的特點，其與智能控制系統相融合的智能照明產品能夠實現照明設備的開關、節能、檢測等功能。智能照明是滿足消費者個性化照明等要求的有效方案，受到照明企業以及智能控制企業的熱捧，具有極大的發展潛力，而LED 作為智能照明產品重要的組成部分，也將受到相關企業的關注。LED 照明正逐步取代傳統照明技術，主導著照明市場的發展方向。LED 照明產品逐漸滲透路燈照明、景觀照明等領域；還可以在農業生產中用作人工光源以提升農業產量；LED 光源具有消炎、殺菌等醫療效果，在人體診斷與治療方面存在廣泛應用。LED 照明應用領域廣，應用前景非常開闊。LED 已經成為當前時代最主要的照明解決方案之一，因此，如何對LED 燈進行準確的壽命預測逐漸得到廣泛的關注。吳志杰等提出了一種新型的基于遺傳算法（GA）優化的誤差反向傳播（BP）神經網絡的壽命預測模型。選取不同公司生產的LED，以LED 光源光通量維持率測量方法（LM-80-08）測試報告中的電流、結溫、初始光通量和初始色坐標作為神經網絡的輸入，LED 在網絡輸入的應力條件下的壽命為輸出，可以預測LED 在任意電流和結溫下的壽命。一般情況下，流明維持壽命（L）是衡量LED 照明的性能、壽命和可靠性的最合適的特性，且目前大多數LED 制造商基于建立壽命預測分析。一般來說，LED 壽命是指一般照明的壽命。本文基于6000 小時或更多的流明數據，采用近似法對LED 進行壽命預測。先利用NLS回歸方法對其進行曲線擬合，根據擬合得到的曲線方程預測LED 的流明維持壽命，再采用近似法處理擬合所得到的數據，進行LED可靠性的分析和評估，并將近似法的評估結果與TM-21標準預測方法進行對比討論。

1 基本方法理論

1.1 NLS回歸方法

NLS 回歸方法是以誤差的平方和最小為準則來估計非線性靜態模型參數的一種參數估計方法。該模型參數的非線性組合的函數取決于一個或多個獨立變量。其中，觀測數據通過函數建模獲得，數據再經過逐次逼近的方法進行擬合。NLS回歸方法的具體步驟如下：

（1）對LED 的光通量數據進行歸一化處理，選取平均值，得到樣本的流明維持率數據。

（2）利用NLS 回歸方法，根據公式（1）對LED的流明維持率數據進行曲線擬合。

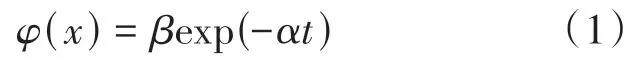
其中，()為在時間的光通量歸一化平均值，即流明維持率；，皆為曲線擬合系數，為常數。

（3）對式（1）進行對數變換，即得到LED 壽命預測模型：

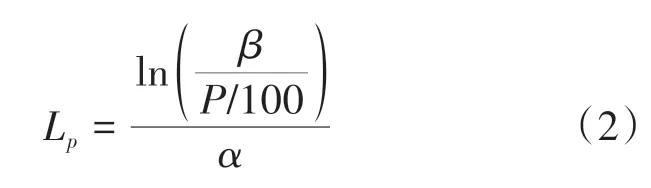
其中，L是LED 的流明維持衰減到初始值的%時的壽命（在本研究中采取=70）。

1.2 近似法

近似法根據一般的退化模型對每個單元的失效時間進行預測，并在退化路徑達到臨界失效閾值D時投影到“偽”失效時間。對于一般的退化路徑模型，假設隨機樣本量為，測量時間為，，，…，t。第臺機組在第次試驗時的性能測量稱為y。因此，退化路徑可以表示為時間性能度量對（t,y），（t, y），（t,y），…，（t, y），對于=1，2，…，n，m表示每個單元的測試時間點

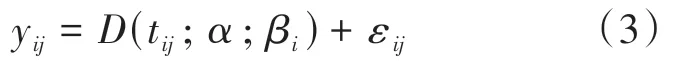
其中，(t;; β)為測量時間t時單元的實際退化路徑。是固定效應向量，每個單位的固定效應保持不變。β是隨機效應向量，它隨不同的單元而變化。ε表示單位在時間t的測量誤差，該時間假設為零均值和方差為的正態分布。

近似法步驟如下：

（1）根 據 數 據（t，y），（t，y），（t，y）…，首先使用NLS 方法估計退化路徑模型的參數（固定效應參數和隨機效應參數β）。

（2）將每個單元的退化路徑模型外推到臨界失效閾值D。當(t;; β)= D時，每個單元的“偽”故障（非實際故障）時間可以預測。

（3）擬合這些“偽”壽命數據的概率分布，并估計分布的相關參數。

（4）根據分析可靠性函數（）、MTTF 評估樣本的可靠性

2 IES TM-21標準基本理論

IES TM-21 是根據LM-80-08 報告推薦的一種流明維護壽命預測方法，TM-21 所用數據即為LM-80-08 報告中數據，IES TM-21 推薦的樣品規模集最小為20，當報告中數據的測試持續時間為6000 小時至10000 小時，數據集中用于曲線擬合的數據應該是最后5000 小時的數據。1000 小時以前的讀數，不用于曲線擬合。對于測試持續時間大于10000小時的數據集，在總體測量持續時間的50%點以后的數據都應用于曲線擬合。換句話說，在/2到之間的數據都應用于曲線擬合。例如，如果測試持續時間是13000 小時，使用的數據應該是6500 小時至13000 小時之間測量所得。如果沒有/2 點的測量數據，則下一個稍低時間點的數據應該包含在擬合數據集內。例如為13000 小時，則每1000 小時采集一次數據,則使用6000 小時至13000小時之間的數據作為擬合數據。

3 實驗結果

3.1 NLS擬合結果

本文數據源于LM-80-08報告，其數據包括了對LED 光通量20個單元的流明維護數據6000個小時的測試點（間隔時間1000 小時），初始1000 小時后以1000 小時的間隔作為擬合數據，按照第1節所示的NLS操作步驟，以每個測試時間的流明維持數據用于使用NLS 方法擬合LED流明衰減曲線，圖1是其中某一單元的預計流明壽命，擬合曲線參數估計和流明壽命結果如表1所示。

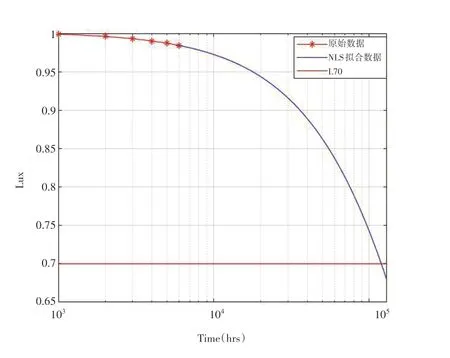
圖1 流明壽命L70測試圖

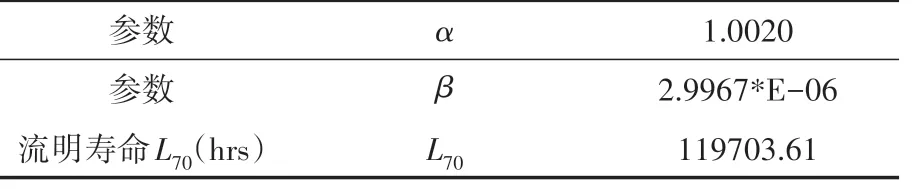
表1 衰減模型參數估計和流明壽命L70

3.2 近似分析法實驗結果

使用非線性最小二乘方法，對每個單元的一般退化路徑模型進行估計，如圖2 所示（左邊是右邊方框的放大），然后通過將每個單元的模型外推到臨界故障閾值（光照減少到70%），預測“偽壽命”，如表2所示。

表2 20個單元退化的參數及偽壽命

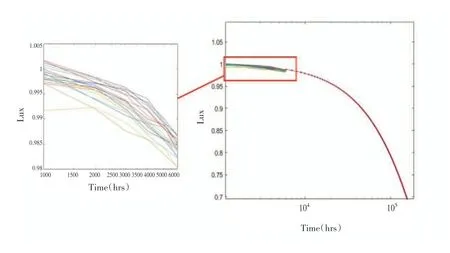
圖2 數據退化路徑

確定從外推法獲得的“偽壽命”的概率分布。為了更精準地對LED 使用壽命進行預測，本文選擇了隨機變量概率密度函數——威布爾分布（Weibull）、對數為正態分布的隨機變量的連續概率分布——對數正態分布（Lognormal）、實值隨機變量的連續概率分布——正態分布（Normal），此三種不同類型的統計模型對“偽壽命”進行擬合。擬合結果如圖3所示。

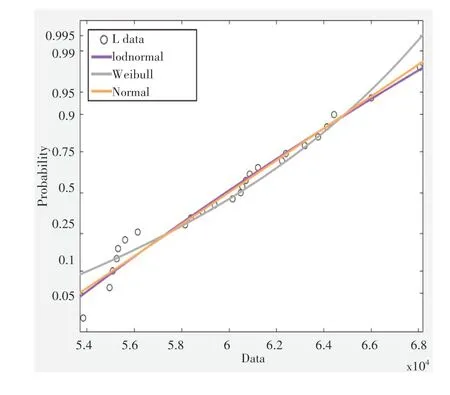
圖3 “偽壽命”統計模型擬合

建立在信息論的基礎上，利用統計模型的擬合優度的方法之一——Akaike 信息準則（AIC），對給定的數據集進行預測誤差估計。AIC不僅可以處理過度擬合的風險和不足擬合的風險，還可以通過驗證分析得到分布滿足威布爾模型時所表現出最好的擬合性能。以下是其可靠性函數：

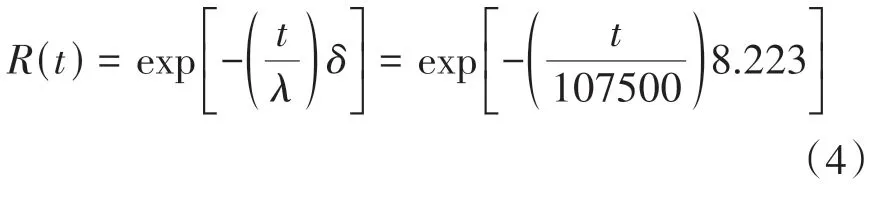
其中與分別為Weibull分布的參數。

最終，利用最大似然估計法可得結果如表3所示。

表3 結果參數

綜上所述，由于近似法忽略了測量誤ε，因此存在一定的局限性。但是，相比與NLS 回歸方法，近似法還提供了更加充足的可靠性信息（可靠性函數、MTTF……），有利于客戶更清楚、全面地了解產品，對市場進行更為有效的評估，以達到精準生產和投入的目的。

4 結語

基于LED 的照明是現代最具影響力的照明時代的技術之一，在節能減排的背景下，社會各界對高效的LED 照明產品的關注程度達到一個新的高度，LED 已經逐漸發展成目前發現的普遍照明應用中，應用范圍廣、成本低、能耗低、穩定性高且高度可靠的光源。不過，迄今為止尚且沒有標準方法可以達到實際測量LED完整壽命的水平。而對LED 進行壽命評估可以在一定的誤差內間接地獲取LED 的壽命數據，因此，對LED 進行較為精確的壽命評估至關重要。為進一步推廣LED 高效、合理的運用，本文采取近似法預測和分析LED 的發光器件壽命。近似法先通過利用NLS 方法，擬合出每個單元的失效時間，然后再對失效概率分布模型進行擬合，從而得出LED 的一般退化路徑模型。與TM-21 標準預測得到的結果相比，近似法不僅可以有效地提供更多的信息，還提供了結果的可靠性，利于開發者更加方便地決策不同壽命LED的市場應用范圍。