建筑空調能耗關鍵變量通用提取方法及工具的開發

沙華晶，許鵬，鐘文智，李云飛

(1.同濟大學 機械與能源工程學院，上海 201804；2.博銳尚格節能技術股份有限公司，北京100089)

建筑能耗占全球總能源消耗的30%以上，而建筑空調系統是建筑服務系統中能耗最高的系統之一[1]。準確的能耗預測是降低建筑空調能耗的重要手段。建筑空調能耗預測主要有兩種方法，第1類是基于物理的模型，也叫白箱模型，采用能耗模擬軟件就屬于這類方法。然而，模擬軟件需要大量的輸入參數，包括建筑外形、圍護結構參數、系統設計及運行參數等，但各參數對能耗的影響程度是不同的，因此，只需確定少數對空調能耗影響重大的變量，建模及計算過程將大大簡化[2]，將這些對空調能耗變化起到決定性作用的變量稱為“建筑空調能耗關鍵變量”，簡稱為“關鍵變量”。第2類能耗預測方法是利用數據驅動模型，也稱為黑箱模型。對于新建建筑或沒有歷史數據記錄的建筑，需要借助相似建筑的歷史能耗進行遷移預測。相較于目標建筑有歷史能耗數據的情況，黑箱模型在以往研究中涉及較少，因為模型的輸入特征必須能夠表征不同建筑能耗的差異，這很難確定，對于不同的建筑類型、氣候區和預測目標，其特征變量不同。已有的建筑能耗遷移預測模型對于輸入特征的選取沒有做深入探討，只是根據作者的經驗和可用的數據資源做簡單的取舍，這就導致模型預測的精度不高[3-4]。

綜上所述，關鍵變量是所有可能對建筑空調能耗產生影響的變量中起決定性作用的少數變量，無論使用白箱模型還是黑箱模型進行能耗預測，關鍵變量的確定都至關重要。尋找關鍵變量是比較復雜繁瑣且計算量很大的過程，因此，筆者開發了基于敏感性分析的關鍵變量自動提取工具，該工具除了可用于確定能耗預測模型的輸入特征之外，還有助于建筑節能改造措施的選擇及能耗模型校驗參數優先級的確定等。

1 全局敏感性分析

敏感性分析方法可分為局部敏感性分析和全局敏感性分析。所謂局部敏感性分析，是指固定待研究參數之外的其他參數，依次分析每個變量對目標變量的影響大小。而全局敏感性分析是指所有變量同時變化，綜合分析各個變量對目標參數的影響。局部敏感性分析計算量小，但忽略了參數之間的相互影響；全局敏感性分析計算量大，但更加可靠，其一般步驟如圖1所示。首先，確定輸入變量和分析目標，建立輸入變量和目標之間的映射關系，可用物理模型或者數據驅動模型建立映射關系；其次，需要確定每個輸入變量的取值范圍和概率分布，并據此進行抽樣，得到輸入變量矩陣，常用的抽樣方法包括拉丁超立方抽樣、蒙特卡洛抽樣等通用抽樣方法，另外，如Morris抽樣與敏感性方法對應；接著，根據輸入矩陣的抽樣值建立若干個模型，計算得到對應的輸出結果；最后，量化各輸入變量對輸出變量的影響程度，得到每個變量的敏感型指標值。表1中列出了采用敏感性分析進行建筑能耗分析的相關研究。通過文獻閱讀分析，筆者發現建筑能耗相關的既有敏感性分析研究側重于某一應用場景，得到的敏感變量也不盡相同，這主要是由于邊界條件及分析目標的不同引起的。在某一場景下得到的敏感變量不能簡單套用到其他場景。另外，既有的建筑能耗相關的敏感性分析研究主要集中在建筑系統的理論設計參數上，如圍護結構熱性能、設備效率等，沒有涉及建筑外形的分析，并且對建筑空調能耗也可能產生重大影響的表征建筑質量和系統運行水平的因素也被忽略了。筆者提出的關鍵變量篩選方法不僅考慮了包括建筑外形在內的理論設計參數，而且考慮了與施工質量和系統運行水平相關的因素，這些因素被稱為“附加因素”。

圖1 全局敏感性分析一般步驟Fig.1 General steps of global sensitivity

表1 敏感性分析在建筑能耗分析中的應用Table 1 Application of sensitivity analysis in building energy analysis

2 關鍵變量提取方法及工具

關鍵變量自動提取工具的框架如圖2所示，是基于Python和Eppy(用于處理EnergyPlus的IDF文件的工具包[15])開發的。用戶需定義的輸入參數包括：建筑所在城市(或天氣文件)；建筑類型；分析目標，可以為冷、熱負荷或是制冷設備能耗。需用戶自定義這些邊界條件的原因是關鍵變量的識別會隨其產生變化。該工具包含3個主要模塊：主程序控制模塊、模型生成模塊和關鍵變量提取模塊。

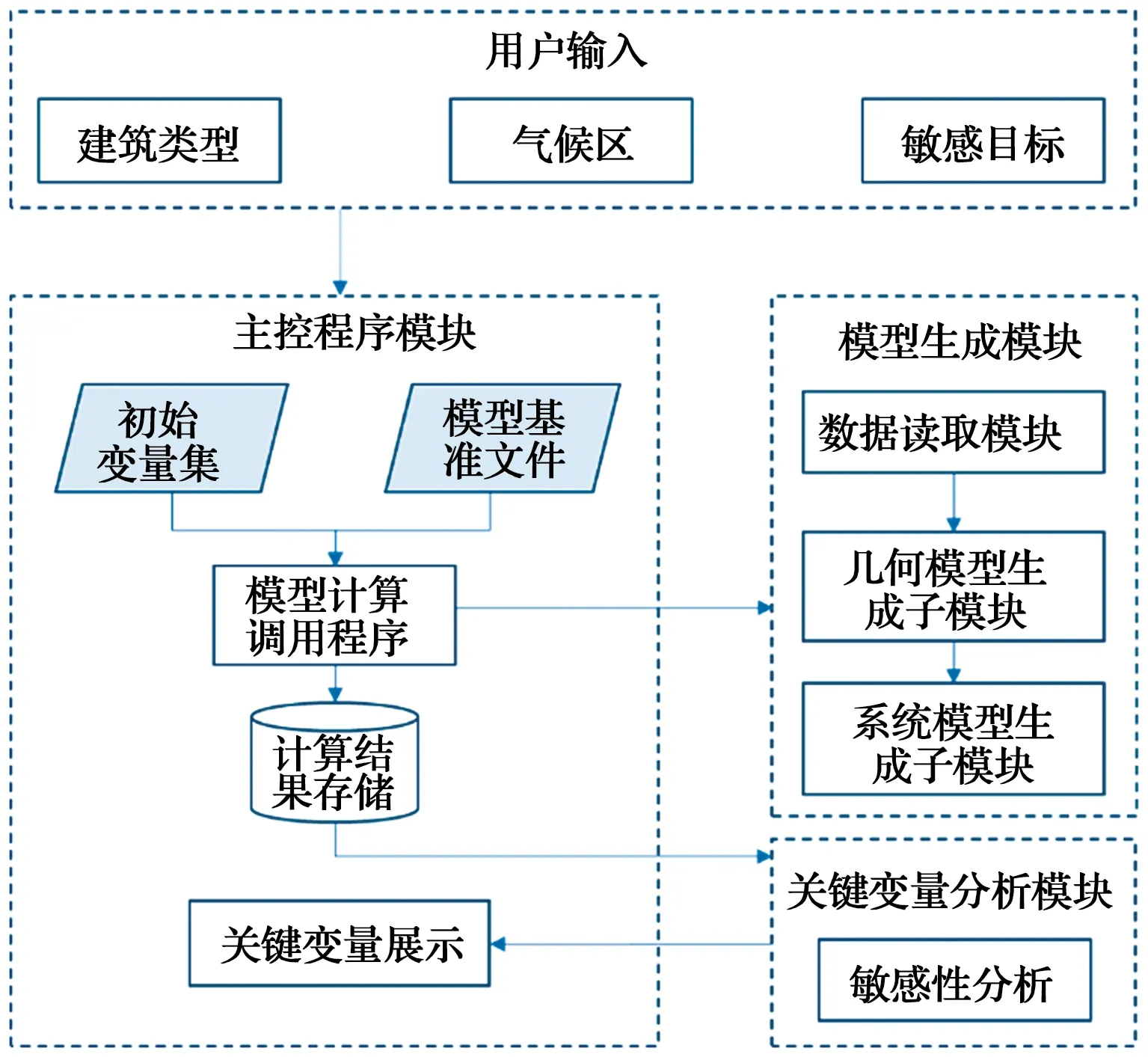
圖2 關鍵變量自動提取工具框架圖Fig.2 Framework diagram of key variable automatic identification

2.1 主程序控制模塊

主程序控制模塊用來讀取用戶輸入信息，生成與目標建筑類型一致的基準模型文件，控制子程序的調用、算例的存儲和讀取以及關鍵變量的展示。用戶輸入信息包括建筑類型、所在氣候區或地區、分析目標(可以為冷、熱負荷或空調設備能耗)，這些信息屬于邊界條件，會影響到最終變量的敏感型排序。

工具基于敏感性分析進行關鍵變量提取，因此，需要首先確定參與分析的初始變量集。關于初始變量集的選取，綜合來講可分為兩類：1)負荷相關變量，如建筑窗墻比、墻體傳熱系數值、照明功率密度等；2)系統相關變量，如空調系統類型、冷機COP等。如果將這兩種參數混合進行抽樣，則樣本容量會變得非常大，計算時間難以接受。因此，分別從建筑負荷相關變量和系統相關變量中選取關鍵影響變量，進行了兩次采樣和敏感性分析。共考慮了23個建筑負荷相關變量和11個系統相關變量。如表2所示，23個負荷相關變量分為4類：建筑外形、圍護結構熱工性能、建筑使用運行以及施工質量。在以往的建筑負荷模擬研究中，通常沒有考慮施工質量(主要指冷橋，因為施工質量較差或年久失修引起)。但其對建筑負荷的影響可能比較大，因此，筆者將其作為潛在的影響變量之一。根據文獻[16]，冷橋對建筑負荷的影響可轉化為建筑墻體傳熱系數的增量，如式(1)。

(1)

式中：UT為考慮冷橋后的墻體傳熱系數；U0為墻體本身的傳熱系數；Atot為非透明墻體面積；冷橋對墻體傳熱系數的影響折算為線性透射率量ψ，W/(m·K);L為對應的線性熱透過率的長度，m。

對于系統相關變量，除理論設計變量外，還包括4個附加變量用以描述系統的運行狀態，如表3所示。

表2 負荷相關初始變量Table 2 Building load related initial variables

表3 系統相關初始變量Table 3 System related initial variables

2.2 模型生成模塊

模型生成模塊的主要功能是建立與輸入參數(即由初始變量集抽樣得到的若干組參數)對應的能耗模型。對于一個能耗模型，幾何部分和系統部分分開建模。幾何模型建立的具體工作流程如圖3所示，主要包括3個部分：基準模型文件讀取；幾何模型生成子模塊；參數修改子模塊。基準模型文件包含目標類型建筑的基本參數設置、時間表設置、功能空間分配等與建筑類型對應的基本信息，這些參數在整個分析過程中保持一致。幾何模型生成子模塊的目標是建立與采樣參數匹配的建筑模型(包括一個建筑的窗、墻、樓板等部分的位置信息以及除空調設備之外的室內設備參數設置)。參數更改子模塊是根據樣本值自動更改模型參數(即人員密度、冷風滲透率及照明功率密度等)，并創建相應的IDF文件。系統生成模型的功能類似，在幾何模型的基礎上添加空調系統設備的相關信息和參數。完成上述準備步驟后，調用建模引擎(即EnergyPlus.exe)進行批量建模計算，并存儲相應的輸出結果，以便進行下一步的敏感性分析。

在所有建筑幾何形狀相關的參數中，建筑體型系數反映了建筑的緊湊度，是建筑形狀的簡化數學表示。較高的緊湊度意味著建筑的表面暴露在室外環境較少，對建筑能耗有很大的潛在影響。但是要對體型系數進行參數分析是比較困難的，需要建立與體型系數對應的建筑外形，目前，現有的參數分析工具(如JEPlus[17])無法達到這一目的。幾何模型生成子模塊解決了建筑物形狀自動匹配采樣參數的問題。筆者建立了建筑外形庫來表征不同的建筑緊密程度，包含了5種基本的建筑形狀，如圖4所示。建筑平面形狀a～e的面積相等，周長遞增，因此它們的緊密程度遞減。筆者提出了sigma因子來表示每個形狀的緊密型。

(2)

建筑體型系數CR，可以用一個函數與sigma聯系起來。

CR=f(sigma,Atotal,NL)

(3)

式中：C為建筑占地面積的周長；A為建筑占地面積；Atotal為建筑面積；NL為建筑層數。通過這種方式，幾何模型生成模塊可以找到最合適的建筑形狀來匹配給定的參數(即建筑面積、層數、體型系數)，從而完成幾何模型的建立。該模塊開發的不同形狀的三維模型如圖5所示。相比于既有工具，開發的工具可分析與建筑體形相關的參數，更加靈活全面。

圖3 幾何模型建立流程圖Fig.3 Flowchart of geometric model

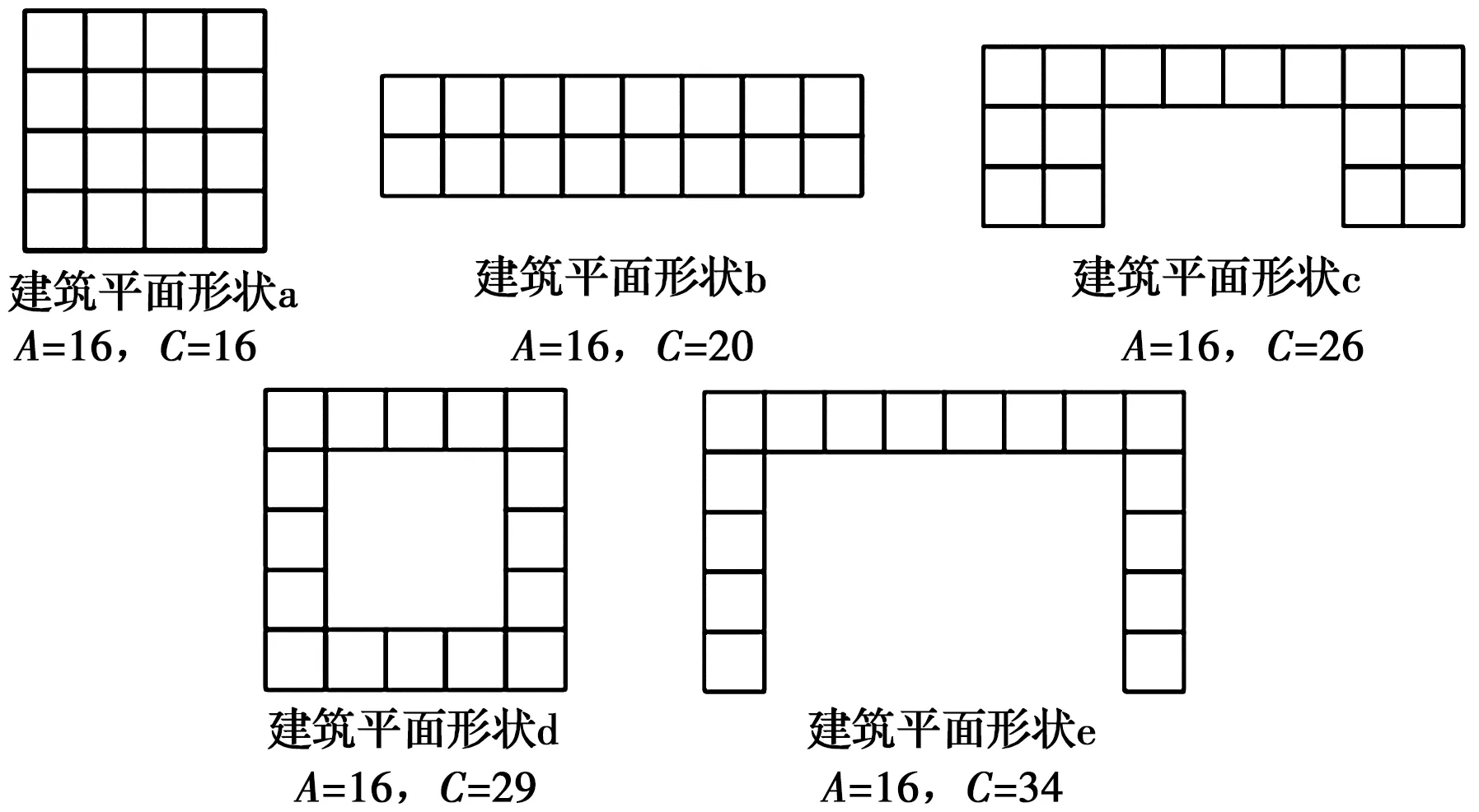
圖4 外形匹配算法平面示意圖Fig.4 Schematic diagram of shape matching

圖5 5種建筑外形

2.3 關鍵變量提取模塊

基于敏感性分析進行關鍵變量的提取。建筑能耗分析常用的全局敏感性分析方法有回歸法、Morris法、Sobol法和FAST法[18]等。考慮到回歸方法和Morris方法的便利性及有效性，筆者采用了這兩種方法。

回歸方法因其易解釋性被廣泛使用，其通過線性方程建立輸入、輸出變量之間的映射關系[19]。每個輸入變量的回歸系數可以用來表示該變量的重要性。兩個常用的衡量指標是標準化回歸系數(SRC)和偏相關系數(PCC)，但這兩個指標只能用于線性模型。SRC和PCC的秩變換(即標準化秩回歸系數(SRRC)和偏秩相關系數(PRCC))通常用于非線性模型。

Morris方法又稱為元效應分析法，因其計算量小而備受歡迎[20]。假設一個模型包含k個自變量Xi,i=1,…,k，每個自變量分為p個水平。因此，輸入空間被劃分為一個p級柵格空間Ω。X的第i維的初等效應定義為

EEi=[y(X1,X2…Xi-1,Xi+…Xk)-

y(X1,X2…Xk)]/Δ

(4)

3 案例分析

3.1 目標建筑

案例分析的目標建筑為酒店類建筑，目標變量為冷機制冷能耗，所處地區為夏熱冬冷地區。建筑模型中有7個功能空間。各個功能空間的面積比例可以反映一個典型的酒店建筑用途，功能空間及對應面積比例分別為：大堂0.1，服務間0.1，餐廳0.075，廚房0.03，會議室0.025，健身房0.02，客房0.65。每個功能空間的使用也與酒店的特點一致，時間表設置參考文獻[21]。需要說明的是，當使用本工具進行其他類型建筑的關鍵變量提取時，功能空間類型、面積配比、時間表需根據分析目標和建筑類型進行修改。

3.2 關鍵變量提取結果

分兩個階段進行關鍵變量提取，第1階段分別采用Morris法和回歸法進行敏感性分析，選取影響建筑負荷相關的關鍵變量。對于Morris方法，在23個輸入參數采樣范圍內抽樣得到240組參數，進行240次模擬計算，并根據計算得到的結果進行敏感性分析，結果如圖6(a)所示(圖中橫坐標符號含義參見表2、表3)。參數μ*的值越高，越敏感。回歸方法采用拉丁超立方采樣方法對23個輸入參數進行采樣，生成6 000個樣本進行模擬計算和敏感性分析。由于建筑空調負荷與各個輸入變量之間呈非線性關系，所以采用SRRC和PRCC作為敏感性指標進行計算，結果如圖6(b)所示。各參數指標的絕對值表示其重要性。圖6(b)中的輸入參數按敏感度遞增順序排序。兩個回歸指標SRRC和PRCC給出了相同的結果。Morris方法和回歸方法的結果對前10個最敏感的變量也有較高的一致性。由于只對高敏感度變量感興趣，因此，這兩種方法的分析結果都被認為是有效的。確定SPC、OPD、INFIL、CR、LPD、SHGC作為建筑熱負荷水平的高靈敏度變量。

在第2階段進行系統相關變量的敏感性分析時，由于Morris方法的特殊性，要求每個變量的變化維度相同，但對于非數值型變量，如系統類型，僅有3個變化水平。因此Morris方法不適用，這部分只使用了回歸方法。數值型變量采用拉丁超立方采樣方法共生成600個樣本，結合兩個非數值變量(風系統類型和水系統類型)的9個組合，共得到5 400個樣本。回歸方法的各敏感性指標排序如圖7所示。確定冷機的COP、AST和WST作為系統相關的關鍵變量。

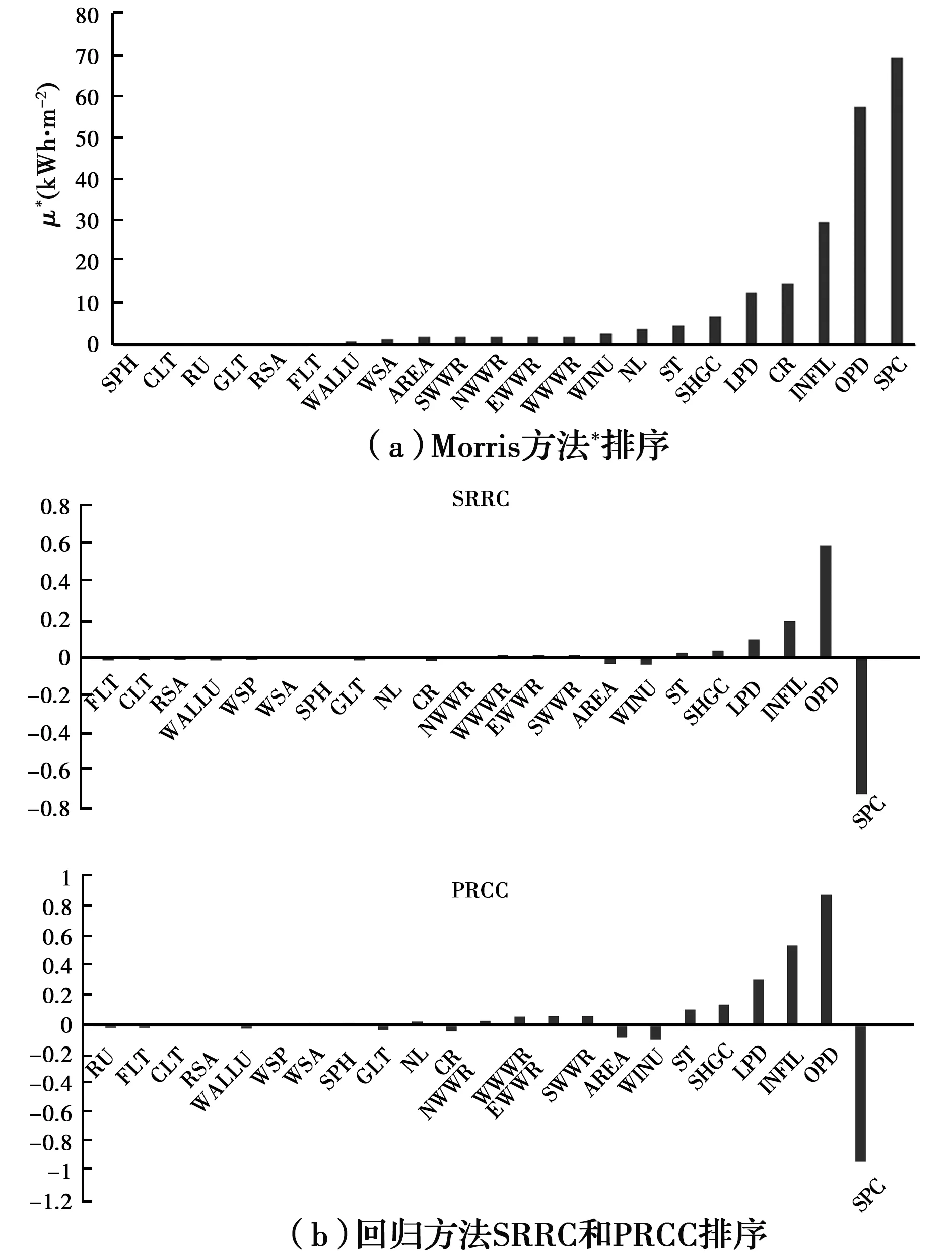
圖6 負荷相關變量敏感性分析結果Fig.6 Sensitivity analysis results of load related

圖7 系統相關變量敏感性分析結果Fig.7 Sensitivity analysis results of system related

3.3 關鍵變量有效性驗證

為了驗證所提關鍵變量提取方法的有效性，基于一棟典型酒店建筑模型進行了對比分析。酒店建筑模型來自美國DOE的典型建筑模型庫[21]，可以反映酒店建筑的基本特征，其外形如圖8(a)所示。在對比分析中共設置了3組模型，基準模型即為原典型酒店建筑模型，沒有經過任何更改。與基準模型相比，對比模型I保持關鍵變量不變(關鍵變量為表4中加粗部分)，與基準模型一致，僅改變非關鍵變量的值。而對比模型Ⅱ同時改變了關鍵變量和非關鍵變量。模型參數設置如表4所示，各參數值的變化都朝著提高輸出變量(即冷機能耗)的方向作改變，對比模型的外形如圖8(b)所示，與基準模型相比，對比模型有相同的面積和層數，外形簡化為體形系數相同的長方體。3組模型的冷機能耗計算結果如圖9所示。很明顯，兩組對比模型的計算結果差異很大。在保持關鍵變量與基準模型相同的情況下，雖然兩組模型的外形不同，但對比模型I的冷機耗電量與基準模型偏差僅為8.6%。而當關鍵變量發生變化時，偏差顯著增加至47.8%。這證明了分析得到的關鍵變量對冷機耗電量有顯著影響，驗證了所提的關鍵變量提取方法的可行性。

表4 對比模型參數設置Table 4 Parameter setting of comparative models

續表4

圖9 基準模型與對比模型的冷機能耗Fig.9 Chiller energy consumption of base model

4 結論

提出一種基于敏感性分析的建筑空調能耗關鍵變量通用提取方法，并基于Python語言開發了相應的關鍵變量自動提取工具。該方法適用于各種建筑類型和分析目標。為了驗證所提方法的有效性，以夏熱冬冷地區酒店建筑為例展開了關鍵變量的提取過程，識別出9個冷機能耗關鍵變量，即SPC、OPD、INFIL、CR、LPD、SHGC、冷水機組COP、AST和WST。對比分析結果表明，這些關鍵變量保留了能夠描述冷機能耗變化特征的大部分信息，從而驗證了所提關鍵變量提取方法的有效性。但是，在使用所提方法時，需注意以下幾點:

1)關鍵變量的選取會受到邊界條件的影響，因此，對于不同的建筑類型或者處于不同氣候區的建筑需要分別進行分析，結果不能簡單套用。

2)不同敏感性分析算法的結果可能略有不同。為了避免漏掉重要的參數，通常使用多種方法的組合結果。

3)關鍵變量的選擇是相對主觀的。用戶可以根據具體情況選擇任意數量的關鍵，選擇變量越多精度越高，但對后續工作(如建立預測模型)來講，信息搜集的成本越大。敏感性分析結果只提供了各變量的理論重要性。在實際工程中，用戶必須根據特定的目的和實際情況(例如經濟、技術等方面等)選擇合適的關鍵變量。