基于MATLAB隨機試驗的砂細度模數公式優化研究

秦超寧，汪麗娟，楊重卿，孫呈鵬，韓 照，喬宏霞

(1.甘肅建投綠色建材產業發展集團有限公司，蘭州 730050；2.蘭州理工大學土木工程學院，蘭州 730050)

0 引 言

目前在我國大部分地區，機制砂已廣泛代替天然砂應用于工業與民用建筑中，隨著政府“限采令”的實施，機制砂還將進一步代替天然砂[1-3]。但與天然砂相比，機制砂的級配往往出現“兩頭大中間小”的級配不良問題[4]。機制砂級配對混凝土性能影響極大[5]，謝開仲等[6]對5種不同級配機制砂混凝土分別進行了力學試驗，認為不同級配下混凝土力學性能隨著機制砂由細到粗，先變大而后變小。王恒[7]采用細度模數為2.62石灰石機制砂配制的C80混凝土具有良好的工作性能。吳永根等[8]研究了細集料對機場道面混凝土耐久性的影響，認為細度模數大于2.64時，混凝土抗凍性、抗滲性下降幅度較快，小于2.64時則混凝土耐磨性下降幅度較快。李瓊等[9]研究發現當再生骨料粒徑為5.0～31.5 mm連續粒徑時，有利于混凝土抗壓強度提高。任青文等[10]通過細觀模擬發現骨料分形譜譜寬與拉伸強度表現出的關系為反相關。目前國內外關于砂粗細程度對混凝土性能影響的研究較多，但對砂粗細程度的表征和計算方法研究較少，王甲春等[11]研究發現細度模數公式中，未涉及粒徑小于0.15 mm部分對質量平均粒徑的影響，而石粉粒徑為0.075 mm以下正屬于未涉及的這部分粒徑，更為準確的細度模數計算將更有利于研究砂粗細程度對混凝土性能的影響。同時機制砂的大量使用帶來的便是石粉問題。機制砂石粉含量對混凝土性能有著顯著影響[12-15]，Gupta等[16]研究發現質量分數30%的石粉可改善混凝土的機械性能和耐久性。Singh等[17]研究發現，在混凝土中使用大理石粉可減少其對環境的影響并具有經濟效益，因此對細度模數公式進一步細分十分必要，須向原公式中融入0.15～0.075 mm及0.075 mm以下兩粒級顆粒含量，以便準確體現石粉對砂級配的影響，也更有利于開展石粉對混凝土性能影響的研究。優化細度模數需要進行大量的篩分試驗，本文利用MATLAB生成大量隨機試驗，以機算代替手算，提高了試驗精度和效率，保證了優選公式的可靠性。通過兩種機制砂樣品及一種天然砂樣品的實操篩分試驗，進一步證明了優選公式的正確性并得到了石粉含量的近似計算公式，在計算細度模數的同時即可得到石粉含量。

1 實 驗

1.1 試驗設計

砂的定義是粒徑小于4.75 mm的巖石顆粒，對小于0.075 mm的顆粒，在天然砂中稱為泥粉，在機制砂中稱為石粉。使用標準GB/T 14684—2011從4.75 mm、2.36 mm、…、0.075 mm七級篩孔的篩余質量進行計量，并給出了各級累計篩余范圍，但國標在計算細度模數時，分子上未涉及0.075～0.15 mm粒級的影響，在分母上未涉及0.075 mm以下粒級的影響[11]，參照原細度模數公式中對不同粒級的設置方法，優化公式應在分子上增加0.075～0.15 mm粒級含量，在分母上減去0.075 mm以下粒級含量。同時由于石粉對機制砂混凝土有著十分重要的影響，這兩個粒級應該納入優化公式中。本次試驗建立在MATLAB隨機試驗rand函數的基礎上，對比了四種不同的細度模數計算方法，分別如式(1)～(4)所示。

(1)

(2)

(3)

(4)

式中：Mx表示國標中規定的細度模數計算方法；Mx1表示優化分母后的細度模數；Mx2表示優化分子后的細度模數；Mx3表示分母、分子均優化后的細度模數；A1、A2、A3、…、A7、A8表示篩孔尺寸分別為4.75 mm、2.36 mm、1.18 mm、…、0.075 mm、0.075mm以下的累計篩余質量分數。最后根據隨機試驗的結果對公式進行優選。

參照國標對2區機制砂顆粒級配的要求，將A1隨機分布范圍設置為0%～10%，依此類推A2-A1為0%～15%，A3-A2為10%～25%，A4-A3為20%～31%，A5-A4為22%～29%，A6-A5為2%～10%，A7-A6為3%～8%。由于A8=100%，當以上各分布范圍集料隨機生成一個數后必定得出一個A8-A7值，同時也必定得出一個細度模數，這樣就可以建立A8-A7與細度模數的一一對應關系，由于細度模數有四個不同的公式，即可在一張圖上得到四個不同細度模數的對比關系，根據覆蓋范圍的大小不同，可以確定不同公式的優劣性，覆蓋范圍越大，區分度越大。

根據兩種機制砂和一種天然砂的篩分試驗進一步驗證結論的正確性，以選取最優的細度模數公式。現行規范規定石粉含量是機制砂中粒徑小于75 μm的顆粒含量。需要通過先烘干，再用水洗去0.075 mm以下顆粒后再烘干后稱量的方法，該方法雖然精確度高，但是操作起來較篩分法費時費力，尤其是水洗后的烘干耗時更長,水洗法石粉含量的計算方式如式(5)所示：

(5)

式中：F表示石粉含量，%；G0表示試驗前烘干試樣的質量，g；G1表示試驗后烘干試樣的質量，g。對篩分后的砂樣，用標準水洗方法測出石粉含量與篩分測出的石粉含量進行對比，作為細度模數公式的補充公式。

1.2 試驗原材料

選取蘭州榆中花崗巖機制砂(granite manufactured sand, GMS)、臨夏永靖凝灰巖機制砂(tuff manufactured sand, TMS)、定西臨洮天然砂(natural sand, NS)，表觀密度分別為2 642 kg/m3、2 743 kg/m3和2 710 kg/m3，試驗用砂樣及表面放大100倍SEM照片如圖1～圖3所示。

圖2 凝灰巖機制砂樣品及表面放大100倍SEM照片

圖3 天然砂樣品及表面放大100倍SEM照片

2 結果與討論

2.1 MATLAB模擬隨機試驗

圖4為分別進行100次、500次隨機試驗石粉含量與細度模數分布圖，由圖4(a)可以看出，在經過100次隨機試驗后Mx、Mx1、Mx2、Mx3分別形成正方形、圓形、三角形、倒三角形四個由點組成的條狀塊，不同塊橫坐標分布的范圍基本相同，均由-10%～27.5%，而縱坐標分布的范圍差距較大，其中倒三角形與圓形塊分布較為水平而正方形與三角形塊分布較為傾斜，說明正方形與三角形塊的細度模數分布范圍要比倒三角形與圓形塊的大，具體分布范圍差如下：Mx2=1.86>Mx=1.50>Mx1=0.74=Mx3=0.74，這說明在相同隨機試驗條件下，Mx2比Mx可以更為細致區分砂的粗細程度，而Mx1與Mx3較原國標公式對粗細程度的區分度則更差。

由圖4(b)可以更加明顯地看出，在經過500次隨機試驗后Mx、Mx1、Mx2、Mx3分別形成的正方形、圓形、三角形、倒三角形四個條狀塊，由于試驗次數較多，在塊內部幾乎看不到空隙，同時可以看出隨機點在塊中心出現的概率較大，在塊邊緣出現的概率較小。不同形狀塊橫坐標分布的范圍擴大到-15%～32.5%，而縱坐標分布的范圍并沒有明顯的擴大，橫坐標分布范圍擴大說明石粉分布范圍擴大，但隨著石粉分布范圍的擴大并不會引起細度模數范圍的變化，只能從縱坐標的區別上研究其分布，與圖4(a)相同的是倒三角形與圓形塊分布較為水平，而正方形與三角形塊分布較為傾斜，說明正方形與三角形塊的細度模數分布范圍要比倒三角形與圓形塊的大，具體分布范圍差如下：Mx2=2.12>Mx=1.67>Mx1=0.76=Mx3=0.76，Mx、Mx1、Mx2、Mx3大小順序與100次隨機試驗是相同的，數值分別比100次隨機試驗大18.82%、11.33%、2.70%、2.70%，說明隨機試驗次數增加，不同算法細度模數的分布范圍均有增大，其中Mx2增大幅度最大，進一步體現出Mx2計算砂細度模數的優越性。

需要說明的是，在圖4中當不同粒級分布隨機取值較大時會出現橫坐標A8-A7出現負值的情況，但這并不影響細度模數公式的優選而且便于直觀觀察。

圖4 分別進行100次、500次隨機試驗石粉含量與細度模數分布圖

2.2 三種砂篩分試驗

為了進一步驗證隨機試驗結果，在模擬試驗后須進行實操篩分試驗。采用四分法將烘干后的GMS、TMS、NS三種砂樣分別稱取500 g，篩孔尺寸從上至下依次為4.75 mm、2.36 mm、…、0.075 mm和篩底，本次篩分除對規范要求的6級篩孔數據進行計量外還對0.075 mm篩孔及篩底的篩余數據進行計量，以驗證更合理的細度模數計算公式，三種砂樣篩分結果如表1所示。

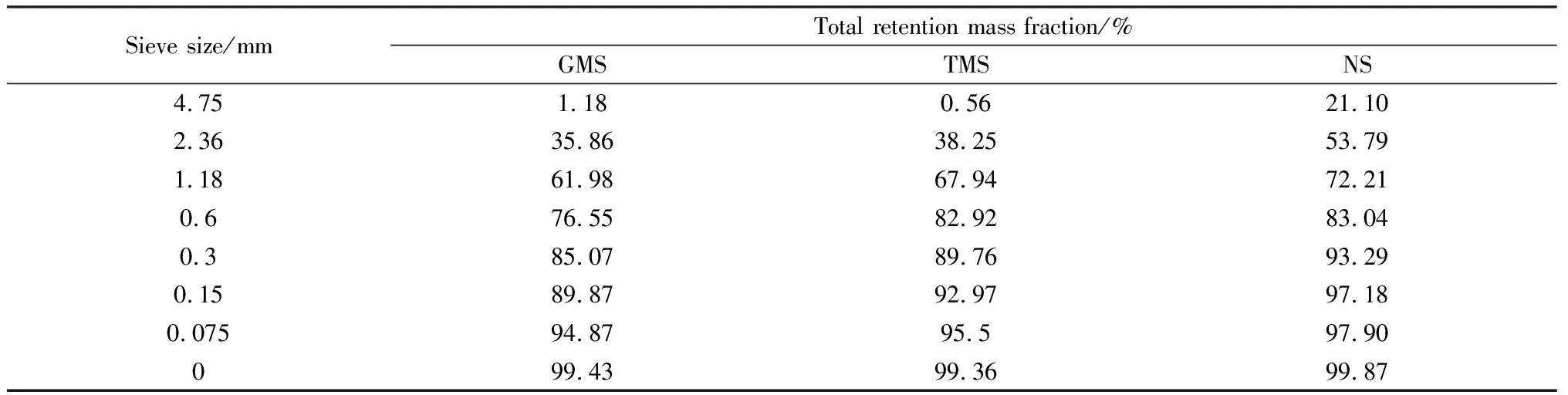
表1 砂樣累計篩余

根據表1結合式(1)～(4)可分別求出GMS、TMS、NS對應的四種細度模數，如圖5所示。

圖5 砂樣細度模數圖

由圖5可知，相同砂樣不同篩孔累計篩余值均相同但算法不同細度模數則不相同，不同砂樣細度模數的相差幅度也不相同，相差幅度越大越能表現出不同砂樣間顆粒級配的差距。花崗巖機制砂、凝灰巖機制砂、天然砂標準細度模數Mx分別為3.48、3.71和3.73，說明三種砂均在粗砂范圍內，GMS相對較細而NS最粗，也可由圖3(a)直觀的看出 NS中平均粒徑大于5 mm的粗顆粒最多。NS的Mx在三種砂樣中最大，但NS的Mx1、Mx2、Mx3卻不是最大，TMS的Mx1、Mx2、Mx3卻是三種砂樣中最大的，這是NS中0.075～0.15 mm粒級顆粒含量較少，式(1)未涉及該粒級，而式(2)、式(4)將分母調整的過小所致。NS中含有4.75 mm以上粗顆粒較多而這部分顆粒并不是砂，因此更為準確的粗砂應是TMS而非NS。可以計算得出TMS的Mx比GMS的Mx大6.61%；TMS的Mx1比GMS 的Mx1大6.04%；TMS的Mx2比GMS的Mx2大7.84%；TMS的Mx3比GMS的Mx3大4.53%，Mx2的相差幅度最大其次是Mx和Mx1，而Mx3相差幅度最小，可以從柱狀圖明顯的看出三種砂樣Mx3整體最大但彼此之間差距較小，這樣對區分不同砂樣的粗細程度極為不利，因此選用不同砂樣進行篩分試驗，進一步驗證了Mx2作為細度模數公式是最優的。

2.3 石粉含量試驗

水洗測得石粉含量(F)與篩分測得石粉含量(A8-A7)都是粒徑小于0.075 mm的顆粒含量，兩者是否存在一定關系需用試驗進一步驗證。國標對機制砂石粉含量的測試方法要求先將砂樣烘干至恒量，再將砂樣浸泡2 h，淘洗干凈濾去小于0.075 mm顆粒后再烘干至恒量，整個試驗過程在10 h左右，而篩分法測試石粉含量僅幾分鐘就可以完成，由于篩分法省時省力效率較高，施工現場往往采用篩分法代替水洗法測試石粉含量，但存在一定誤差。本文以三種砂樣石粉含量測試的篩分試驗與水洗試驗為對比找出了兩種方法測得石粉含量的近似關系，并用SEM進行微觀驗證以降低兩種測試方法之間的誤差。根據表1、式(5)可分別求出GMS、TMS、NS對應的篩分石粉含量和水洗石粉含量，如圖6所示。

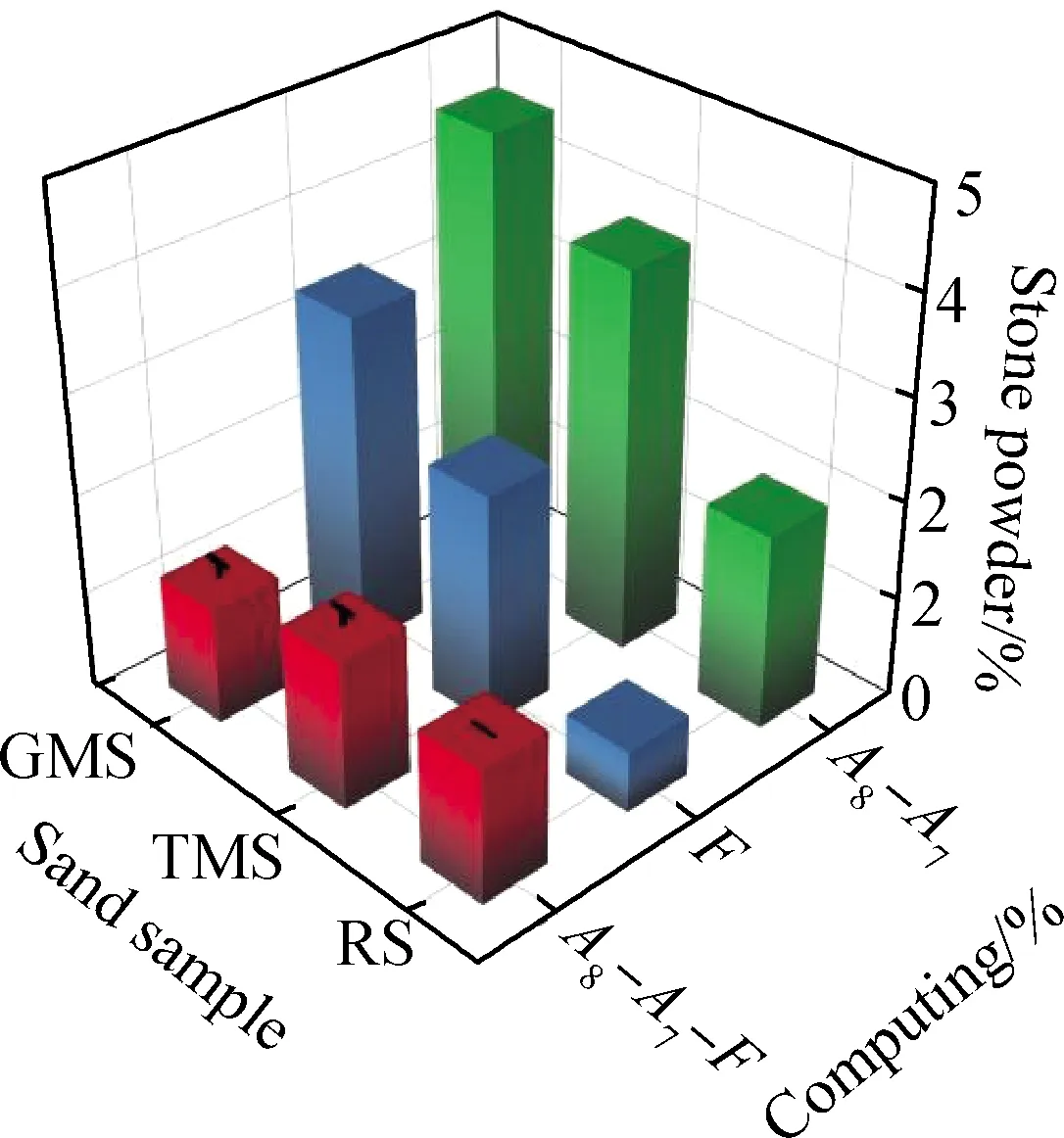
圖6 石粉含量不同測試法圖

根據圖6可知，三種巖性的砂采用篩分法測得的石粉含量均小于水洗法。因為在水洗的過程中，較大砂粒上吸附的石粉幾乎會被全部洗下，而顆粒之間的吸附作用使篩分法只能篩除部分吸附的石粉。GMS、TMS、NS篩分法比水洗法測得的石粉含量分別小1.18%、1.51%、1.35%，由圖1～圖3中的SEM照片可以看出TMS的表面粗糙程度最小，其次是NS，最大的是GMS，說明顆粒表面越粗糙對石粉的吸附量就會越大，篩分法與水洗法測得石粉含量的差值就會越大。雖然兩種方法測出的石粉含量相差幅度(A8-A7-F)不同，但比較穩定，相差幅度均值為1.35%，誤差線最大值為0.167，最小值為0，標準偏差0.13，說明吸附在較大顆粒上，不能通過篩分法篩除的0.075 mm以下顆粒的含量是一個定值，由于不同細集料巖性表面粗糙程度不同，這個定值存在一定波動性，經過線性回歸得出公式(6)：

A8-A7=F+1.346 6%(R2=0.984 8)

(6)

式(6)說明石粉含量測試方法中篩分法與水洗法滿足斜率為1，常數項為1.346 6%的一次函數關系。采用篩分法測試石粉含量簡便快捷且不用在洗砂前后對砂樣進行烘干，洗砂前后的烘干要求砂樣烘干至恒量，會花費大量時間，篩分法在測試細度模數的同時只需增加一檔孔徑為0.075 mm的方孔篩，即可測得石粉含量，式(6)又進一步降低了篩分法與水洗法的誤差。式(3)、(6)構成包含了快速測試石粉含量的砂細度模數全部優化公式。

3 結 論

(1)分別通過100次和500次四種細度模數與石粉含量的隨機生成試驗，發現在分子上涉及0.075～0.15 mm顆粒的Mx2在描述細度模數時變化范圍最大，最有利于表征不同粗細程度細集料的區分度。采用優化后的細度模數計算公式將更有利于研究砂粗細程度對混凝土性能的影響。

(2)通過GMS、TMS、NS三種砂樣的實操篩分試驗，發現Mx2在衡量砂樣粗細程度時相差幅度最大并可以有效排除大于4.75 mm顆粒對細度模數計算的不利影響，進一步證明了Mx2在表征不同粗細程度細集料方面的優越性。

(3)提出了石粉含量測試方法中篩分法與水洗法滿足一次函數關系，斜率為1，常數項為1.346 6%，可進一步減小篩分法估算石粉含量的誤差，采用篩分法測試石粉含量大幅度減少了石粉含量的測試時間，有利于生產、科研效率的提高。