六自由度機械臂運動學分析與仿真研究

何浪，謝明紅，劉馳弋

（華僑大學機電及自動化學院，福建廈門 361021）

0引言

隨著世界“工業4.0”進程的不斷深化以及“中國制造2025”戰略的全面部署，世界制造業的發展將日漸趨于數字化、網絡化、智能化[1]。多自由度工業機械手臂在工業自動化領域中扮演著一個不可或缺的重要角色。在切割、焊接、噴涂、裝配、碼垛等多個工業領域有著非常廣泛的應用，有效地降低了生產過程中的勞動力成本，提高了社會生產力，推動人類社會的工業自動化水平的發展。六自由度機械臂控制系統研究主要包括運動學分析和軌跡插補兩部分核心內容，是機械臂精確、平穩、高效工作的重要保障。

傳統的機械臂運動學控制系統的開發是基于機械臂物理實體設計過程，缺乏計算機軟件的仿真模塊，需要通過花費更多的時間力氣調試機械臂，而且最終結果往往也不夠準確[2]。當前隨著計算機技術的飛速發展，各種仿真技術也被廣泛應用到機械臂的控制系統研究當中，避免了直接在機械臂上調試，通過構建精度較高的機械臂模型，在仿真平臺上模擬實現機械臂的實際運動情況，最后再通過對機械臂實體的調試，設計出更加精準、高效的機械臂控制系統。基于此，本文以錢江RH6型的六自度串聯工業機器人為研究對象，通過對機械臂的運動學分析及軌跡規劃的分析研究，在VS2017軟件開發平臺上，開發模擬機械臂運動過程的仿真軟件。

1 運動學建模與求解

機械臂的運動分析采用的是由Denavit和Hartenberg在1955年提出的D-H參數法[3]。在機械臂的每個連桿上固連一個坐標系，以此來描述連桿在空間中的位置狀態，通過齊次變換矩陣來描述各個坐標系之間的相對關系，從而來表示各連桿之間的相對位姿，在根據各連桿之間的位姿關系建立機械臂的運動學方程，求取機械臂的正逆解。

1.1 D-H模型構建

本文研究的錢江RH6型機械臂由6個轉動關節串聯而成。在對機械臂進行運動學分析之前需要對機械臂進行建模，確定每一個連桿上的坐標系。為了方便對連桿的描述，對各連桿進行標號，從固定基座開始為0號連桿，第一個可動連桿為1號連桿，直到機械臂的最末端連桿為6號連桿，連桿編號完畢開始確定連桿坐標系，連桿坐標系的建立需要遵循以下原則：1）按照笛卡爾坐標系的規則自由設定0號連桿的坐標系及其坐標原點位置；2）機械臂各關節均為轉動關節，其連桿軸線由右手定則確定；3）將各連桿的上一個連桿的關節軸定義為該連桿坐標系的Z軸，Z軸方向可自由選定，通常平行的Z軸的方向相同；4）將相鄰兩連桿i軸和i+1軸的軸線的公法線設置為i軸連桿坐標系的X軸，X軸方向由i指向i+1，i軸和i+1軸的交點或公垂線與i軸的交點作為連桿坐標系的原點；5）各連桿坐標系的Y軸由右手定則確定。

機械臂的連桿坐標系建立完畢之后，需要確定各連桿的參數。連桿參數主要包括連桿夾角θi、連桿扭角αi、連桿長度ai、連桿偏距di。根據實驗室機械臂的原始尺寸可以得到機械臂的D-H參數表，如表1所示。

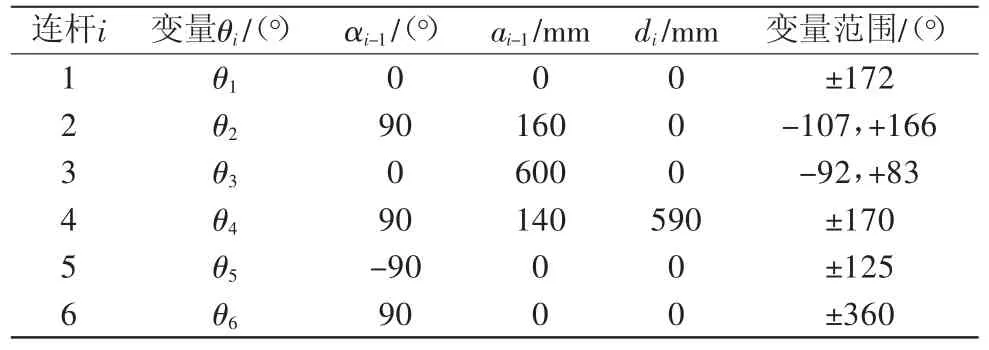
表1 錢江RH6型機械臂連桿參數表

建立機械臂的D-H模型如圖1所示。

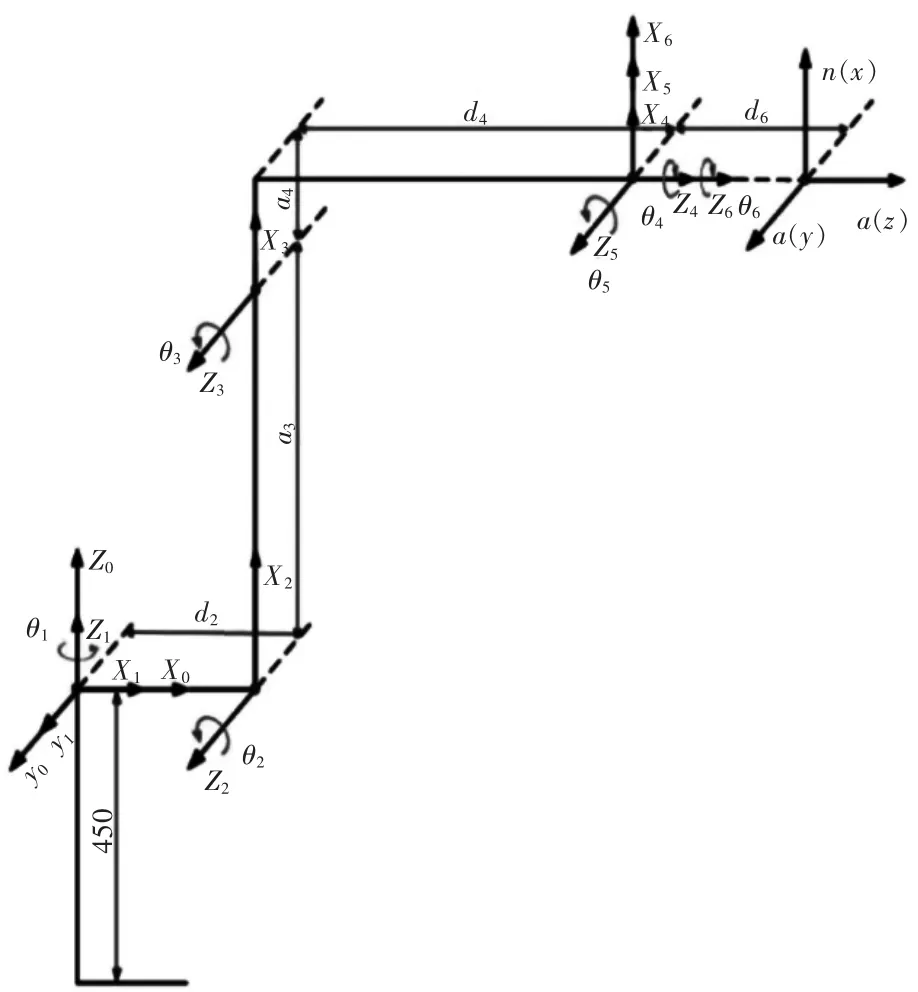
圖1 錢江RH6型機械臂D-H模型

根據所定義的連桿坐標以及連桿參數，能夠推導出相鄰兩關節坐標的矩陣變換關系為

1.2 正逆運動學分析

機械臂的正逆運動學分析主要包括正運動分析和逆運動學分析。正運動學分析是根據已知的各關節旋轉角度來獲取機械臂的末端位姿。逆運動學是根據機械臂的期望末端位姿反求各關節角的大小[4]。正運動學求解能夠得到機械臂末端位姿的唯一解，而逆運動學求解既有可能得到多組封閉解，也有可能出現沒有封閉解的情況。在應用過程中需要結合機械臂的實際應用場景及各關節轉角限制約束來選取最優解。

機械臂的正運動學分析首先需要根據上文推導的相鄰連桿坐標系的齊次變換矩陣及各連桿的參數來求解各相鄰連桿之間坐標系的齊次變換矩陣。

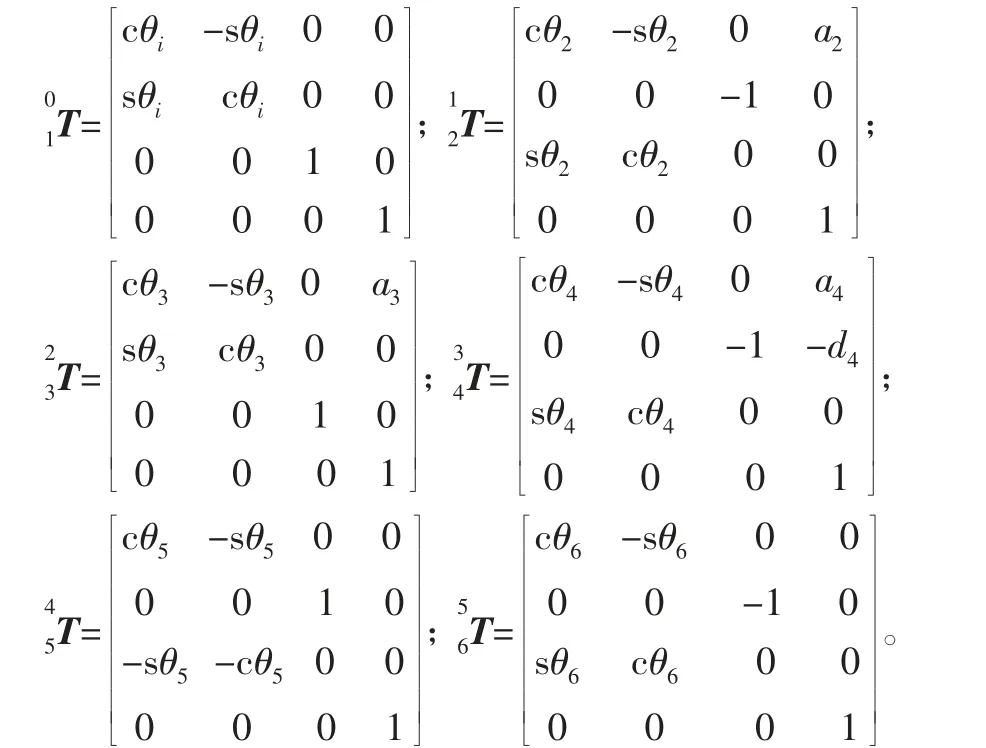
由上述各個連桿坐標之間的齊次變換矩陣,通過鏈式規則可以求解得到機械臂末端點和基座之間的齊次變換矩陣，即為機械臂的正運動唯一解：

式中：ci、si分別表示sin（i）、cos（i）；cij、sij分別表示sin（i+j）、cos（i+j）。

機械臂的逆運動學分析是通過給定機械臂的末端位姿來求解機械臂6個關節角的轉動大小。由于本文所研究的錢江RH6型機械臂滿足Piper原則，即機械臂的3個關節軸相交于一點存在著封閉解。因此，通過求解封閉解的方式來進行機械臂的逆運動求解分析。機械臂前3個關節角確定的是末端執行器的位置坐標，后3個關節角確定了末端執行器的姿態坐標，在逆解求解過程中先求解前3個位置關節角再求解后3個姿態關節角。

由上面的計算便可以求解出機械臂的前3個關節角，由計算結果可知θ1存在著兩個解，對應的θ3存在著4個解，由于θ2能夠由θ1和θ3唯一確定，所以前3個關節角總共存在4組解。最后，還需要確定出空間位置的最優解，根據機械臂各關節角的限制范圍以及角度變化的原則可以獲取機械臂空間位置的最優解。

根據所求得的θ1、θ2、θ3進一步求解機械臂的后3個關節角。在式（5）中，將等式兩邊的（1,3）和（3,3）元素對應相等，可以求解得到θ4的大小：

令式（14）兩邊元素（1,1）和（3,1）對應相等求解可得出θ6的大小：

通過上述求解，得到了機械臂的剩下3個關節角的大小。理論上，機械臂前3個關節角有4組不同的解，由于通過機械臂的腕關節的翻轉可以獲得同樣的姿態，所以機械臂后3個關節角有2組不同的解。因此，機械臂理論上有8組不同的封閉解。根據機械臂各關節角的限制范圍以及角度變化的原則可以從中選取出機械臂的最優解，來控制機械臂達到指定的目標位姿。

2 機械臂軌跡插補算法

插補算法是數控加工的指揮者，是機械臂控制系統的核心內容[5]。插補的過程就是根據NC代碼離散成多段微線段的過程，常見的插補算法有空間直線插補算法和空間圓弧插補算法。插補算法按插補方式又有脈沖增量插補和數據采樣插補。本文采用的是數據采樣插補即時間分割法，將加工一段曲線的時間劃分為若干個相等的插補周期，每經過一個插補周期就進行一次插補運算，計算出該插補周期內機械臂各軸的進給量。采用時間分隔法要求插補算法有較快的運算速度，能夠在1 ms的插補周期內完成插補運算以及其他相關的運算及動作。因此，本文采用常見的空間直線和圓弧插補算法來實現機械臂的軌跡插補，插補周期設置為1 ms，每個插補周期的插補步長Δl由插補周期和進給確定。

2.1 空間直線插補

直線插補是根據已知直線軌跡的終點坐標，分解出在每個插補周期各個軸的運動分量，如圖2所示。

圖2 直線插補

假設直線軌跡的終點坐標為pe（xe，ye，ze），首先需要確定當前插補周期的起點坐標。當當前加工直線軌跡為第一個程序段，那么將坐標原點設置為起點。否則，我們將上一段加工軌跡的終點設置為起點，將所確定的起點坐標定義為po（xo，yo，zo），可以求出直線軌跡的總長度l：

當直線軌跡插補到最后一個插補周期時，剩下的直線長度llast≤Δl時，將最后一個插補周期的步長設置為Δlδ=llast，再分別投影到各個坐標軸上，可以得到各軸的進給量。最后直到直線余量llast=0時，完成直線插補過程。

2.2 空間圓弧插補

空間圓弧插補是將NC代碼所確定的圓弧軌跡離散為多段微線段。在空間坐標系中，確定一段圓弧軌跡需要3個點，在NC代碼中給出的是圓弧的起點坐標、終點坐標及圓弧軌跡的圓心坐標。假設圓弧軌跡的終點坐標為pe（xe，ye，ze），圓心坐標為po（xo，yo，zo），首先確定圓弧軌跡的起點坐標，若當前加工直線軌跡為第一個程序段，那么將坐標原點設置為起點。否則，我們將上一段加工軌跡的終點設置為起點，將所確定的起點坐標定義為ps（xs，ys，zs）。

根據已知的條件可以求得以下內容：

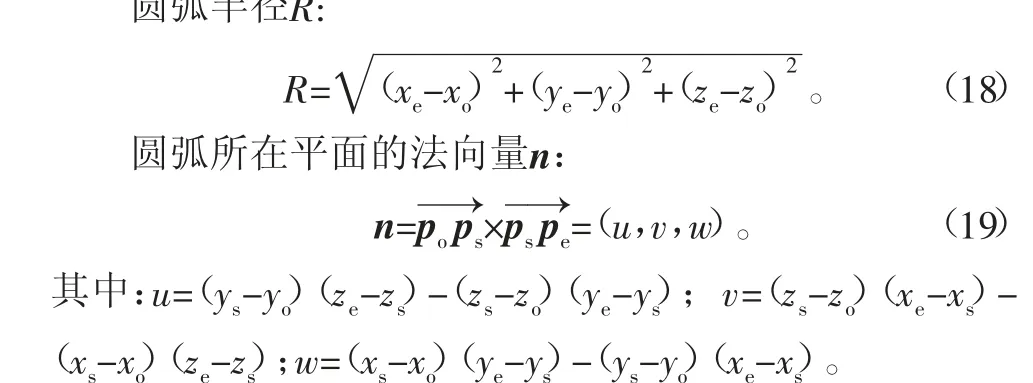
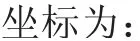
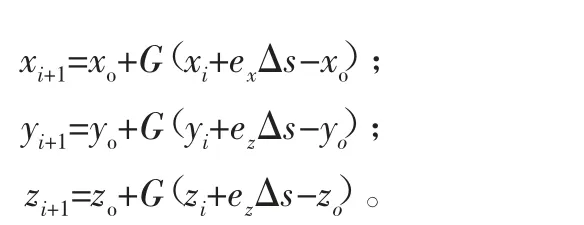
當剩余圓心角θδ小于步距角Δθ時，圓弧插補進入到最后一個插補周期，此時令步距角等于剩余圓心角，計算出各軸進給量。當θδ=0時，圓弧插補結束。

六自由度機械臂不僅僅是計算機械臂空間位置的插補，還需要考慮機械臂空間姿態的插補。在本文采用的是均勻變化的方式進行姿態插補，假設起點姿態為ps（αs，βs，γs），終點姿態為pe（αe，βe，γe），那么可以得到每個插補點pi的姿態公式為：

根據上面的直線與圓弧的插補算法，可以求得各個插補周期中插補點的空間位姿pi（xi，yi，zi，αi，βi，γi），通過逆運動學分析，將笛卡爾坐標系下插補點的空間位姿求逆解得到關節坐標系下各軸的轉動角度pi′（θi1，θi2，θi3，θi4，θi5，θi6）,通過關節坐標系下各軸的角度來模擬仿真機械臂的運動過程。

3 OpenGL仿真軟件開發

在機械臂的控制系統研究過程中，仿真環節是必不可少的一環，通過對機械臂的運動過程的仿真能夠模擬出機械臂末端執行器的實際運行軌跡，驗證運動學算法及插補算法的準確性。本文采用的是基于MFC窗口框架下的OpenGL來進行機械臂的實時仿真。OpenGL是一種純軟件的圖形庫函數，不受硬件條件和不同操作系統的限制，支持多種語言開發，能夠為圖形軟件開發提供非常豐富的圖形API接口函數。本文的OpenGL仿真軟件開發的主要流程包括三維建模和仿真實現兩部分。在調用OpenGL庫函數前，需要在基于MFC框架中配置OpenGL的開發環境。在VS2017的軟件開發平臺中已經集成了OpenGL32.lib庫函數，再通過導入glut32.lib即可完成OpenGL開發環境的配置。

3.1 三維建模

三維建模主要包括機械臂的運動軌跡建模和機械臂的實體建模兩部分內容。機械臂的運動軌跡模型的建立是通過解析NC代碼獲取加工圖形每一工步的頂點坐標，將其存儲到數組當中，根據G01、G02、G03分別區分加工軌跡的直線、順圓、逆圓。直線軌跡的繪制直接通過調用OpenGL中的直線繪制函數glBegin（GL_LINES）和glEnd（）。圓弧軌跡的繪制需要對圓弧進行離散，離散結果是許多微線段，當線段數量足夠多的時候，軌跡便能夠無限逼近圓弧，將這些離散出來的點根據直線繪制的方式繪制出來便能夠實現圓弧軌跡的建模。圖4是NC代碼馬單環的軌跡建模效果圖。

圖4 馬單環軌跡模型仿真

機械臂實體建模首先需要通過三維軟件分別畫出機械臂6個連桿的實體模型，將其保存為obj格式，obj文件是通過點的坐標來描述三維模型，在obj文件中主要由關鍵字及點位坐標組成，在通過obj文件導入三維模型的過程中需要先解析obj文件，提取不同關鍵字下的數據將它們分別保存到數組中，然后再通過調用OpenGL中的三角形繪制函數glBegin（GL_TRIANGLES）和glEnd（）來繪制模型的各個三角面，最后組合成機械臂的3D模型。

完成了機械臂的實體建模之后還需要實現其動態仿真過程，機械臂的動態仿真過程其實質就是圖形的幾何變換問題，可以通過調用OpenGL 庫函數中的函數glTranslatef（x，y，z）來實現機械臂模型在X、Y、Z方向的平移動作，調用函數glRotatef（Angle_x，1，0，0）、glRotatef（Angle_y，0，1，0）、glRotatef（Angle_z，0，0，1）來分別實現機械臂繞基座標系的X、Y、Z軸的轉動，調用函數glScalef（m_xScalse, m_yScalse, m_zScalse）可以實現機械臂模型的放大和縮小動作。

3.2 仿真實現

建立了機械臂的三維模型并實現了機械臂的動態仿真的模擬，接下來便可以進一步完成機械臂的仿真軟件的開發。機械臂在工業領域的實際應用中主要有點動和聯動兩種運動方式，對應在仿真軟件中需要分別模擬出機械臂的點動控制和聯動控制。點動控制的實現是通過給定機械臂各關節需要轉動的關節角，通過運動學求正解算法確定機械臂末端執行器的位姿，同時在仿真軟件界面上實時顯示機械臂末端執行器的位姿。聯動控制是控制機械臂的六軸聯動到達指定的目標位置，從而實現目標軌跡的運動。

軟件客戶端指定機械臂的NC代碼，仿真軟件需要讀取并解析指定的NC代碼，通過直線和圓弧插補算法將NC代碼離散成許多間隔很小的點，通過機械臂逆運動學求出各軸的關節角，將它們保存到自定義的數組中實時傳遞給OpenGL的旋轉函數，并且在軟件界面實時顯示機械臂末端執行器的動態位姿，從而實現對機械臂按照目標軌跡的動態仿真。

4 結語

本文通過對錢江RH6型機械臂的運動學分析和插補算法的研究，采用OpenGL模擬仿真了機械臂在實際加工過程中的運動情況，開發了一套基于MFC的六自由度機械臂仿真軟件。軟件能夠實現機械臂的實時點動控制和聯動控制兩種不同的運動模式，實時跟蹤機械臂末端執行器的運動軌跡及各軸的旋轉角度，能夠較好地實現機械臂動作過程的模擬仿真，對后期在機械臂上的實操作業有非常重大的指導意義。