融合圖注意力的多特征鏈接預測算法

張雁操，趙宇海，史 嵐

東北大學 計算機科學與工程學院，沈陽110169

鏈接預測是復雜網絡研究工作中重要研究方向之一，是指通過已知的部分網絡結構預測網絡中兩個節點是否存在鏈接。這些鏈接可能是缺失的或未被觀察到的，也可能是未來網絡演變過程中可能產生的。因此鏈接預測可以幫助人們更好地補全網絡或理解網絡結構生成及演化的機制。

作為一個典型的交叉學科，鏈接預測已經成為數據挖掘領域重要的研究方向之一，其應用場景涉及許多領域。例如，在生物領域，可用于預測蛋白質之間的相互作用，在Yeast網絡中，大部分細胞間相互作用尚不為人知；在社交領域，可用于預測社交活動的產生或消失；在交通領域，可以用于交通線路規劃、城市道路規劃；在推薦領域，可以進行商品推薦、好友推薦等。

目前有一類簡單的鏈接預測方法是基于相似函數的鏈接預測，也稱作啟發式方法。該類方法假設：節點傾向于與其相似的節點形成鏈接。通過定義相似性函數計算兩個節點的相似性，然后將節點對的相似性得分按遞減順序排列，位于排序頂部的鏈接更有可能為丟失鏈接或者未來可能相連的鏈接。

基于計算相似性所需節點的距離可將啟發式方法分為三種：一階、二階及高階。一階啟發式僅僅涉及兩個目標鏈接節點的一跳鄰居節點，例如共同鄰居（common neighbors，CN）、Jaccard 指數（JA）、優先連接指數（preferential attachment index，PA）等。二階啟發式是通過目標鏈接節點的兩跳鄰居計算相似性的，例如Adamic-Adar 指數（AA）、資源分配指數（resource allocation index，RA）等。還有需要更大范圍甚至是整個網絡的相似性度量方法，稱為高階啟發式，例如PageRank（PR）、Katz指數（Katz index，KI）、SimRank（SR）、隨機游走（random walks，RW）等。盡管這類方法實踐效果良好，但是對于鏈接的存在性有很強的人為假設。對于不同類型的數據集，相似性函數往往有著不同的定義。例如，CN 假設若兩節點有更多的共同鄰居，則它們更有可能相連，這種假設在社交網絡中可能是正確的，但是在蛋白質交互網絡（protein-protein interaction networks，PPI）中被證明是無效的；JA 通過計算兩個節點的完整鄰居集合中共同鄰居的比例度量節點相似性；PA 假設兩個節點之間形成鏈接的概率隨著節點度的增加而增加。

另一類近年來被用于鏈接預測任務的是節點嵌入算法。本文按節點嵌入算法獲取向量表示的過程將其分為兩類：第一類是通過保留節點的局部鄰域信息，用于特征提取、節點分類、鏈接預測等任務的算法，例如DeepWalk、LINE、N2V（node2vec）等。第二類算法從全局角度挖掘每個節點的潛在特征信息，通過保留節點的結構特征相似性、社區信息、全局排序信息等生成節點嵌入向量，例如struc2vec、M-NMF（modularized nonnegative matrix factorization）、NECS（network embedding with community structural information）、PRUNE（proximity and ranking-preserving unsupervised network embedding）等。

node2vec 節點嵌入算法第一次將鏈接預測作為下游任務評估算法性能。它從廣度優先和深度優先兩個角度，使用有偏隨機游走最大限度地保留節點的鄰域信息，并利用低維向量表示進行鏈接預測等任務。PRUNE 設計了保留多種特征信息的目標函數，使用孿生神經網絡進行無監督學習，將得到的向量表示用于鏈接預測等任務。另外由網絡的同質性原理，同一社區中的節點比不同社區間的節點更相似。M-NMF 和NECS 節點嵌入算法利用矩陣分解，以學習網絡的社區結構、保留節點的社區信息為目的，在鏈接預測任務中取得了良好的效果。但是節點嵌入算法不具有任務特定性——不是針對鏈接預測任務設計的，被用于特征提取、節點分類、鏈接預測等多個下游任務，無法捕獲對鏈接預測最有效的信息。

在監督學習中幾乎所有的分類器都可以用于鏈接預測。Lichtenwalter 等人提到將多種分類器用于鏈接預測，包括決策樹、支持向量機、近鄰算法、多層感知器、樸素貝葉斯等。Cukierski等人利用隨機森林取得了良好的結果。針對啟發式方法和節點嵌入算法的缺陷，Zhang 和Chen 首次提出將啟發式看作預定義的圖啟發式特征，利用神經網絡學習合適的啟發式進行鏈接預測，并據此提出了WLNM（Weisfeiler-Lehman neural machine）算法。首先提取包含指定節點數的局部子圖，然后利用啟發于Weisfeiler-Lehman算法提出的PALETTE-WL標記方法獲得子圖節點標記，最后根據節點標記重構子圖鄰接矩陣，輸入到全連接神經網絡中訓練。進一步的，Zhang和Chen提出了目前表現最優異的鏈接預測算法SEAL（learning from subgraphs，embeddings and attributes for link prediction），其中使用的圖神經網絡DGCNN（deep graph convolutional neural network），具有更好的圖特征學習能力，且該算法允許從節點特征中學習，包括DRNL（double-radius node labeling）節點標記和node2vec 節點嵌入特征。但是SEAL 算法具有以下幾個問題：

（1）局部性：對于目標鏈接，該方法通常考慮一跳或兩跳局部子圖，利用的特征如局部子圖的鄰接矩陣、局部子圖的DRNL 獨熱編碼標記矩陣和node2vec向量表示等。通過神經網絡的學習，只能獲得低階啟發式特征。

（2）特征無效性：由于目標鏈接的局部子圖可能是不連通的，會導致DRNL 節點標記矩陣具有較強的特征無效性（見1.1 節）。

（3）節點無偏性：在圖卷積的過程中，未考慮到不同節點對于鏈接存在性的影響應該不同，因此對于局部子圖中節點信息的聚合過程應該是有偏的（見1.1 節）。

針對SEAL 算法存在的問題，本文提出了融合圖注意力的多特征鏈接預測算法ADNSL（learning from double-radius node labeling，node2vec and struc2vec for link prediction with attention mechanism），主要貢獻如下：

（1）針對上述問題（1），提出了一種支持不同類型特征輸入的鏈接預測算法。在局部特征生成模塊中，該模型將局部角度的節點嵌入特征輸入到圖神經網絡，學習預定義的啟發式特征。在全局特征提取模塊中，利用struc2vec 從全局角度提取節點的結構特征，通過重構圖上的隨機游走生成游走序列，并得到節點嵌入向量，進而提升鏈接預測性能。

（2）針對上述問題（2）和（3），在局部特征生成模塊中提出雙向無參注意力圖卷積，可以有效彌補特征無效性和節點無偏性（見1.1 節）。

（3）為了降低模型復雜度，在全局特征提取模塊中提出了有效的迭代公式，將struc2vec的重構多層圖轉化為聚合圖，在保留結構特征相似性的同時，可以有效減少I/O 時間、內存消耗及磁盤消耗（見1.2 節）。

（4）在八個不同領域公開經典數據集上的實驗表明，ADNSL 相比于多個基準模型，ACC 和AUC 值有十分明顯的提升。對于平均度較小的數據集NS、Power 和Router，AUC可有10個百分點以上的提升（見2.5 節）。

1 融合圖注意力的多特征鏈接預測算法

本章將詳細介紹融合圖注意力的多特征鏈接預測算法模型ADNSL。首先，針對SEAL 算法的局部性，給出了ADNSL 的整體框架圖（圖1）；然后，給出了局部特征生成模塊的介紹，針對SEAL 的特征無效性和節點無偏性，給出了雙向無參注意力圖卷積過程；接著，介紹了全局特征提取模塊，并針對重構多層圖的特性，提出迭代公式用于生成聚合圖。

圖1 ADNSL 框架Fig.1 Framework of ADNSL

如圖1 所示，針對SEAL 算法的局部性，ADNSL框架主體分為兩部分，上方為局部特征生成模塊，下方為全局特征提取模塊。局部特征生成模塊利用局部子圖的DRNL 節點標記矩陣和node2vec 節點嵌入矩陣作為特征輸入，經過多次圖注意力卷積得到多感受野的節點特征向量，然后將每一層圖卷積的輸出結果拼接，并通過排序池化層和一維卷積層，生成局部特征向量，詳細過程在圖2 中展示。全局特征提取模塊使用全局角度struc2vec 方法提取節點嵌入向量，根據多跳度序列計算輸入圖中節點間的結構距離，并利用結構距離重構原圖生成多層圖，再利用迭代公式得到聚合圖，通過聚合圖上的隨機游走，提取目標節點的全局特征向量，詳細過程在圖3 中展示。之后，將兩個模塊得到的特征表示融合，輸入到全連接層預測鏈接是否存在。整個框架通過有效的多特征融合，可以合理地利用節點嵌入特征，明顯地提升鏈接預測的性能。

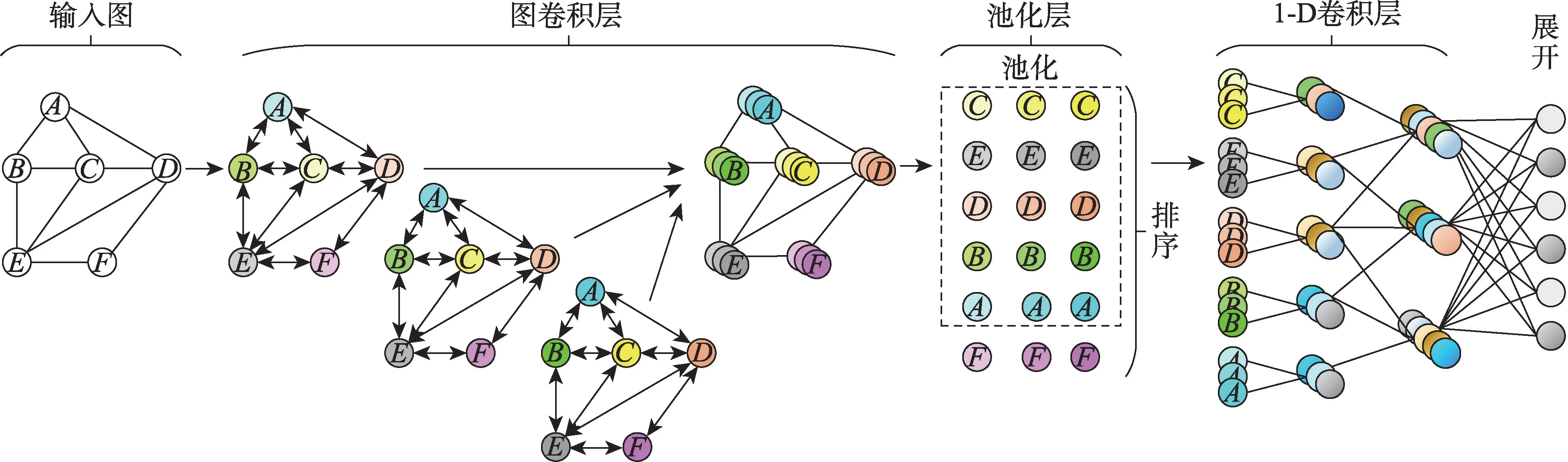
圖2 局部特征生成模塊Fig.2 Local feature generation module

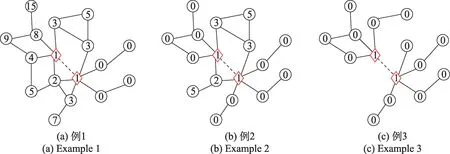
圖3 DRNL 特征無效性Fig.3 Ineffectivity of DRNL features

1.1 局部特征生成模塊

給定無向無權圖=(,)，=||，表示節點的集合，表示邊的集合，表示節點個數。對圖，有鄰接矩陣和特征矩陣∈R，其中由DRNL節點標記矩陣和node2vec 節點嵌入矩陣拼接而成。如圖2 所示，利用圖注意力卷積生成局部特征。

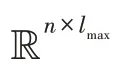
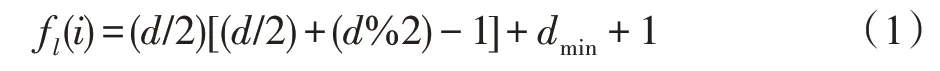
其 中，=d+d，=min(d,d)，d=(,) 和d=(,)分別表示節點到目標節點和的距離，(/2)和(%2)分別是除以2 的整數商和余數。特別地，f()=f()=1；若(,)=∞或(,)=∞，則 f()=0 。需要注意的是，在計算距離(,)和(,)時，路徑不可通過目標節點和。

式（1）所示的DRNL 節點標記哈希函數具有如下特性：對于局部子圖中的任意兩個節點、及目標節點、，當(,)+(,)≠(,)+(,)時，(,)+(,)＜(,)+(,)?f()＜f()；當(,)+(,)=(,)+(,) 時，(,)(,)＜(,)(,)?f()＜f() 。因此子圖中的節點到兩個目標節點的距離之和越小，則標記值越小；子圖中的節點到兩個目標節點的距離之和相等時，距離之積越小，標記值越小。

利用式（1）計算得到的節點標記如圖3 所示。菱形節點表示目標節點和。除了標記為0 的節點外，局部子圖中標記越小的節點，對于目標鏈接的存在性越重要。由于計算距離時，路徑不可通過目標節點，局部子圖中可能含有大量標記為0 的節點。這些節點的標記值對于鏈接的存在性是無意義的，因此DRNL 節點標記矩陣具有較強的特征無效性。

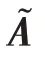
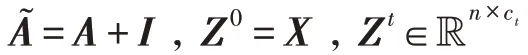
啟發于圖注意力網絡（graph attention networks，GAT），在上述兩個問題的基礎上，提出融合注意力機制的圖卷積過程，可以更加注重有效的特征信息，更好地捕捉節點特征的差異性。對于圖中的任意兩相鄰節點、，在+1 層，有注意力系數：

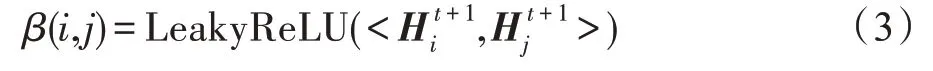
其中，＜*,*＞表示向量的內積。本文ADNSL 中注意力系數的計算過程與GAT 有兩點不同：（1）特征矩陣H是子圖中的節點聚合鄰居節點的特征后得到的，在計算某兩個節點的注意力系數時，除了考慮這兩個節點的特征外，還考慮了它們所有鄰居節點的特征，這顯然更合理。（2）在得到特征矩陣H后，采用式（3）計算注意力系數，該過程不涉及可訓練參數，可以有效降低計算復雜度。

在歸一化前，圖注意力權重見圖4。隨著圖注意力卷積層數的加深，節點和節點對于、之間鏈接存在性的影響逐漸增大，而節點對于鏈接的存在性的影響降到最小。在此基礎上，對應于圖2 中排序池化層所展示的，可以更果斷地將節點的特征向量去除。

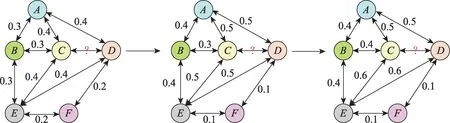
圖4 softmax 前圖注意力權重示意圖Fig.4 Graph attention weights before softmax

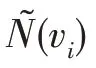
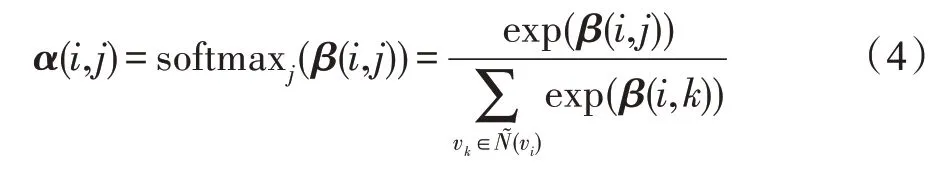
在得到歸一化后的雙向注意力權重后，第+1層的輸出為：

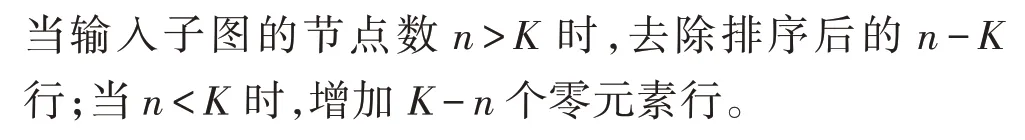
1.2 全局特征提取模塊

本模塊利用struc2vec 節點嵌入算法提取結構特征。該算法利用圖中每對節點不同鄰域范圍的結構距離構建多層圖，并利用迭代公式將多層圖轉化為聚合圖，然后利用隨機游走和SkipGram 生成節點序列和節點嵌入向量。具體過程見圖5，可分為四步。

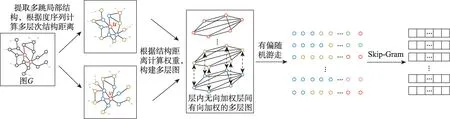
圖5 全局特征提取模塊Fig.5 Global feature extraction module

（1）度量結構相似性

度量結構相似性時不使用節點或邊的屬性信息，也不基于任何特定的相似性度量。此處的相似性僅僅依賴于節點的度，這種相似性是分層的，隨著鄰域范圍不斷增加，可以捕獲更精確的結構特征相似性。對于兩個節點，如果它們的度相同，它們是結構相似的，而若它們的鄰居具有相同的度序列，則它們更加結構相似。

對于圖=(,)，=||表示圖中的節點數。若有圖中的節點，R()定義為的第跳點集。對于?，()表示中節點的有序度序列。令為圖的直徑，指圖中任意兩個節點間距離的最大值。對于圖中任意兩節點、的跳子圖，=0,1,…,，考慮它們在層的結構距離定義為：

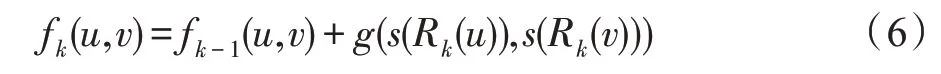
其中，=0，且|R()|,|R()|＞0，度量了兩個有序度序列的距離。注意只有當節點和均有跳鄰居時，f(,)才有意義，當或不存在跳鄰居時，與在多層圖的第層無邊相連，見式（9）。

采用動態時間歸整（dynamic time warping，DTW）算法計算度序列的距離。對于兩個有序度序列、，匹配它們中的每一個元素、，每一對元素的距離定義為：

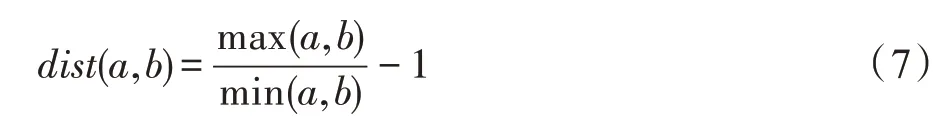
和的距離即為所有元素對距離之和。

另外，為了降低DTW 算法計算結構距離的時間復雜度，令′、′分別為度序列、的壓縮形式，=(,)，=(,)分別是′、′中的元組，元組中和表示度值，和對應和出現的次數。式（7）調整為：

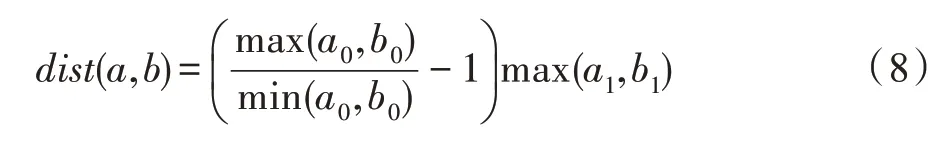
（2）構建多層圖

利用結構距離構建多層圖。由于多層圖內存消耗較大，為了降低復雜度，在度量結構相似性時沒有必要計算每個節點與其他-1 個節點的相似性，即多層圖的每一層并非完全圖。將原始圖中的節點度按序排列，對每個節點，在度序列前后各選取lb個節點與其連接。另外當多層圖的層數接近時，跳鄰居數較少，度序列的長度相對較短，f(,)與f(,)差別不大。故對于層數，選取一個固定值′＜，能有效降低構建多層圖的計算和內存需求。

此時構建的多層圖是層內無向加權層間有向加權的。式（9）表示層內權重，在第層，兩個點、的結構距離越遠，權重越小。只有當f(,)有意義時，、在層才有邊相連。

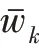
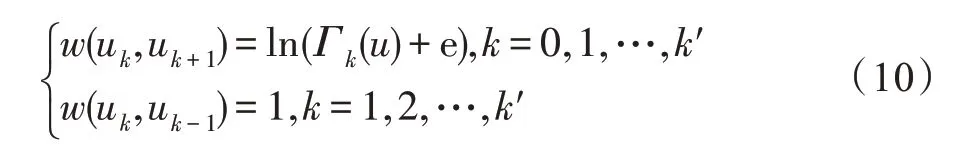
（3）生成節點序列

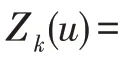
進一步地，為了降低I/O 時間、內存消耗以及磁盤消耗，利用式（12）的層間權重將多層圖中的信息匯聚到同一層，生成聚合圖。為此要求每一層節點間的連接情況完全相同。

在多層圖中，每個節點與2×lb個節點相連，但是根據式（6）和式（9）可知，每一層的連接情況可能不同，因為當或在跳無鄰居時，f(,)無意義，此時,在層無邊相連。為了使每一層的連接情況完全相同，對于在第0 層有邊相連的節點對,，若它們在＞0 層無邊相連，則令w(,)=0。

在保證每層節點間連接情況相同后，提出迭代公式（14），利用多層圖中的信息生成聚合圖。

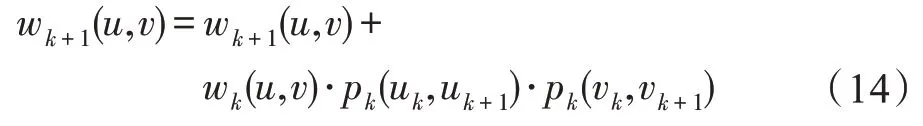
根據式（6）、式（9）和式（11）可知，在低層結構特征不相似的節點對在高層一定不相似；兩個節點結構特征越相似，節點間邊的權值越大，轉移概率越大。因此，如圖6 所示，對于節點(,)在信息聚合過程中有三種情形：

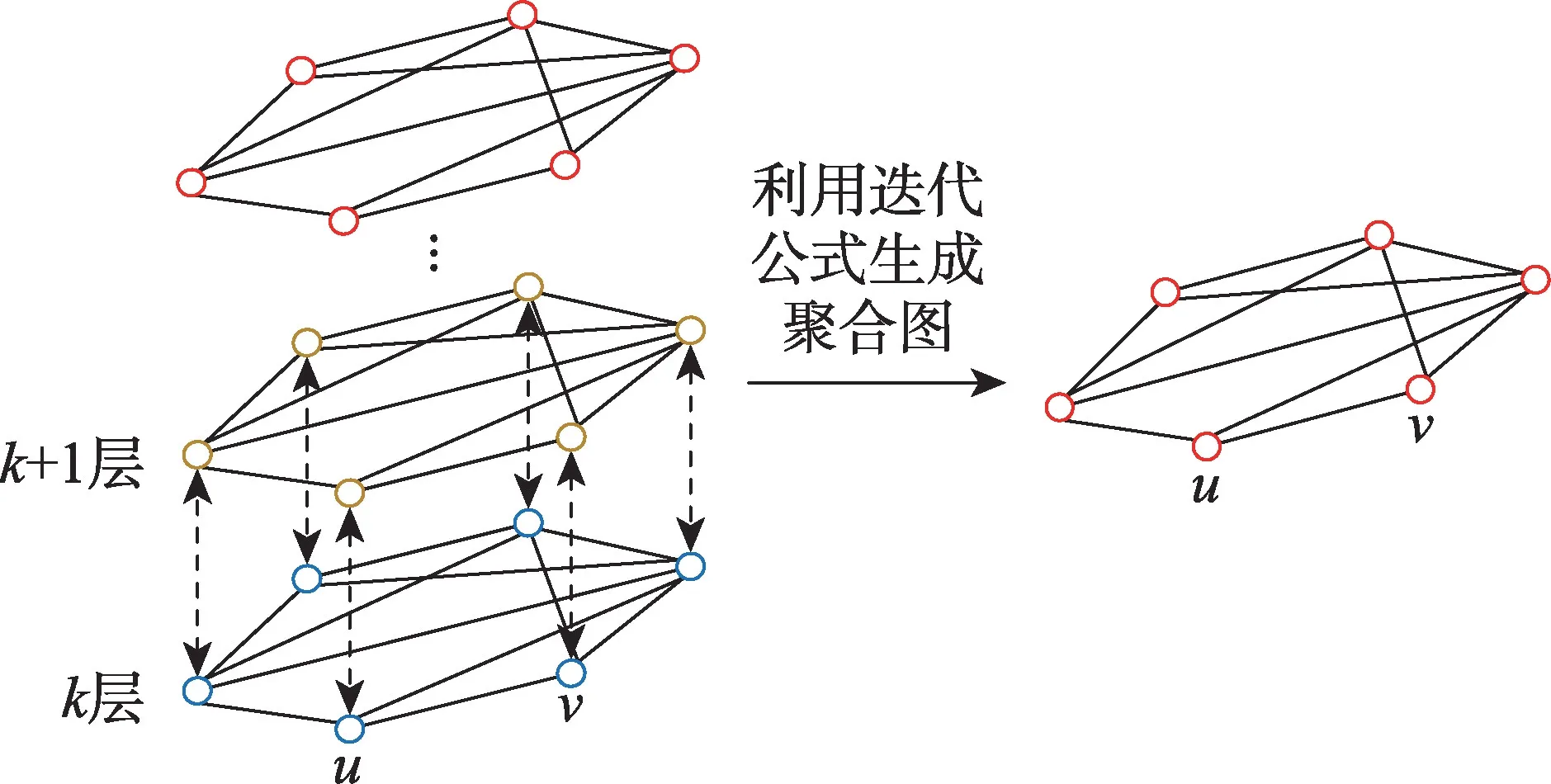
圖6 聚合圖Fig.6 Agglomerative graph

若節點對(,)在層結構特征不相似，則在+1 層一定不相似，由多次小權值累積，可以得到更加精細的權重。

若節點對(,)在層結構特征相似，在+1 層也相似，低層的權重匯聚到高層降低了其影響力，傾向于依賴高層權重進行隨機游走。

若節點對(,)在層結構特征相似，在+1 層不相似，通過迭代公式減小從層獲得的權值，傾向于利用+1 層的權重與情形2 區分。

綜上，利用式（14）生成的聚合圖具有三個顯而易見的特性：低層的權重匯聚到高層降低了其影響力；結構特征越相似的節點對之間的權重越大；聚合圖上的有偏隨機游走不存在層的切換，相較于多層圖，聚合圖的內存和磁盤占用更少。

（4）生成節點嵌入向量

在聚合圖上通過有偏隨機游走得到節點序列后，利用自然語言處理模型SkipGram 生成嵌入向量。給定一個節點，SkipGram 的目標是最大化其上下文出現在序列中的概率，其中節點的上下文由以其為中心的大小為的窗口得到。

對于這一任務，采用分層softmax 優化策略，通過霍夫曼二叉樹計算條件概率。對于窗口內的節點∈，在霍夫曼二叉樹中有一條由樹節點構成的路徑,,…,b，其中為根節點，b即為節點，有：

其中，是二元分類器邏輯回歸。

2 實驗

本章在第1章的基礎上，將衍生出的模型ASEAL（learning from subgraphs，embeddings and attributes for link prediction with attention mechanism）、DNSL（learning from double-radius node labeling，node2vec and struc2vec for link prediction）以及最終模型ADNSL與啟發式方法、節點嵌入算法還有神經網絡模型在八個數據集上進行了全面的對比。本章接下來主要介紹數據集、評價指標、負注入、模型結構及超參數設置，并進行實驗對比分析。

2.1 數據集

實驗包括八個真實數據集：USAir（美國航空線路網絡）、NS（網絡科學研究人員協作網絡）、PB（美國政治博客網絡）、Yeast（蛋白質交互網絡）、C.ele（秀麗隱桿線蟲的神經網絡）、Power（美國西部電網）、Router（路由器級因特網）和E.coli（大腸桿菌代謝產物成對反應網絡）。八個數據集涉及的領域有交通網絡、社交網絡、生物網絡等。它們的具體信息見表1，其中||為網絡中節點數量，||為網絡中邊的數量。

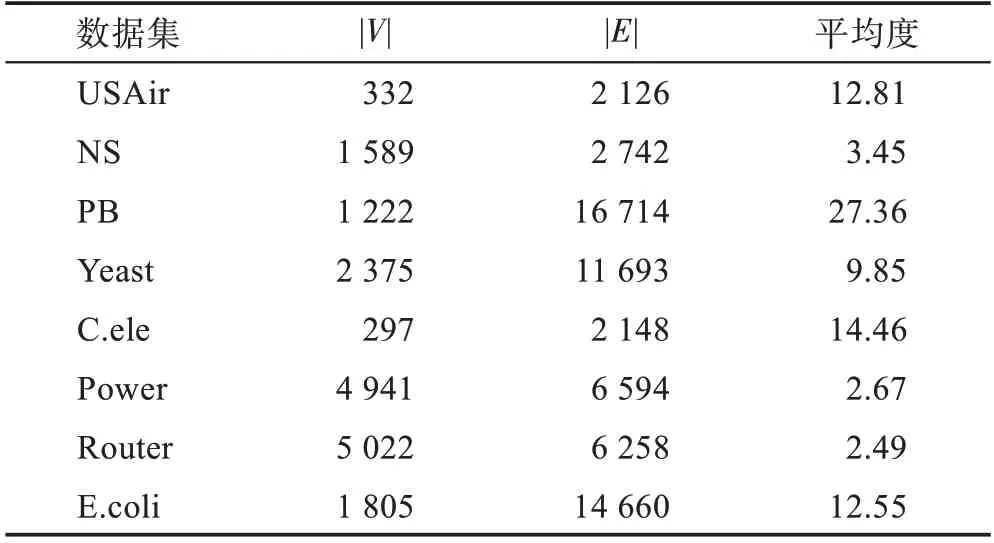
表1 實驗數據集Table 1 Experiment datasets

2.2 評價指標

本文的實驗結果主要使用ACC（準確率）和AUC（ROC 曲線下面積）評估二分類的優劣。每個實驗進行30 次，取平均值作為實驗結果。

對于每個數據集，將網絡中存在的鏈接隨機分為訓練正例和測試正例，并選取等量的不存在鏈接的節點對作為訓練負例和測試負例。在實驗中，考慮了50%和90%的鏈接作為訓練正例兩種情況。另外，在生成節點嵌入特征之前，需將測試正例從網絡中移除以防止測試集泄露。

2.3 負注入

假設給定網絡=(,)，有訓練集正例?，以及訓練集負例?=?。在網絡上利用節點嵌入算法得到的嵌入向量作為節點特征。若該過程記錄了網絡中某些邊的存在信息，即，則在神經網絡訓練過程中，僅僅對這部分信息進行擬合就能得到很好的訓練效果，但是這會導致模型的泛化性能很差。因此，對于存在這一問題的節點嵌入算法，通過負注入將訓練集負例加入網絡中，即在′=(,?E)上學習節點嵌入向量，可以有效地提高泛化性能。

在局部特征提取中，特征矩陣包含節點標記矩陣和節點嵌入矩陣兩部分。如果直接在上利用node2vec 提取節點嵌入向量，由于隨機游走過程依賴于網絡中存在的邊，該過程會記錄邊的存在信息，圖神經網絡只需要對這部分信息進行擬合即能得到很好的訓練效果，但是在測試時模型的泛化性能很差。因此node2vec 需要在負注入后的′=(,?E)上學習節點嵌入向量。

與node2vec 不同，在利用struc2vec 提取全局結構特征時，使用負注入是不合理的。struc2vec 在生成向量表示過程中，僅僅利用了節點度信息，且隨機游走是在重構的聚合圖上進行的，未涉及原圖中任何邊信息。若struc2vec 在負注入的圖上生成節點嵌入向量，反而會對節點度和節點結構特征產生較大影響，嚴重影響性能。經過實驗發現，不使用負注入的struc2vec 可以保留更有效的結構特征相似性，對鏈接預測的效果有顯著提高。

2.4 模型結構及超參數設置

局部特征生成模塊的輸入為目標鏈接一跳或兩跳子圖，∈{1,2}。對于SEAL 和DNSL，為了適應內存，數據集PB 和E.coli 選擇=1，其余數據集=2。對 于ASEAL 和ADNSL，數 據 集NS 和Power 選 擇=2，由于加入了雙向注意力機制，為了適應內存，其余數據集=1。另外，對于E.coli，限制子圖中最大節點數為150。特征矩陣中node2vec生成的節點嵌入向量為128 維，node2vec 有偏隨機游走參數=1，=1，游走路徑數為10，路徑長度為80，SkipGram 中窗口大小為10。

局部特征生成模塊采用四個圖卷積層，通道數分別為32、32、32、1。為了方便起見，僅使用最后一層通道排序，排序后，截取行，其中值使得60%的子圖的節點數大于。接下來是兩個一維卷積層，輸出通道數分別為16 和32。第一個卷積層的輸入維度為97×1，卷積核大小為97×1，卷積核個數為16，步長為97，輸出維度為×16，之后的最大池化層的卷積核大小為2，步長為2。第二個卷積層的卷積核大小為5×16，卷積核個數為32，步長為1。圖卷積層使用tanh 作為非線性函數，在其他層中使用ReLU 作為激活函數。

全局特征提取模塊中，struc2vec 將′=6 的多層圖的信息匯聚到單層圖，生成32 維的節點嵌入向量，并將64 維的目標鏈接節點向量表示輸入到全連接層。與node2vec 相同，對于聚合圖上的隨機游走，每個節點的游走路徑數為10，路徑長度為80，SkipGram中窗口大小為10。

局部特征生成和全局特征提取模塊的輸出維度均固定為64 維。全連接層的隱藏單元數為128，dropout比率為0.5。

2.5 實驗結果及分析

表2 和表3 分別是50%和90%的鏈接作為訓練正例的情況下，模型性能的對比，其中帶下劃線的AUC為次優的，加粗的AUC 為最優的。

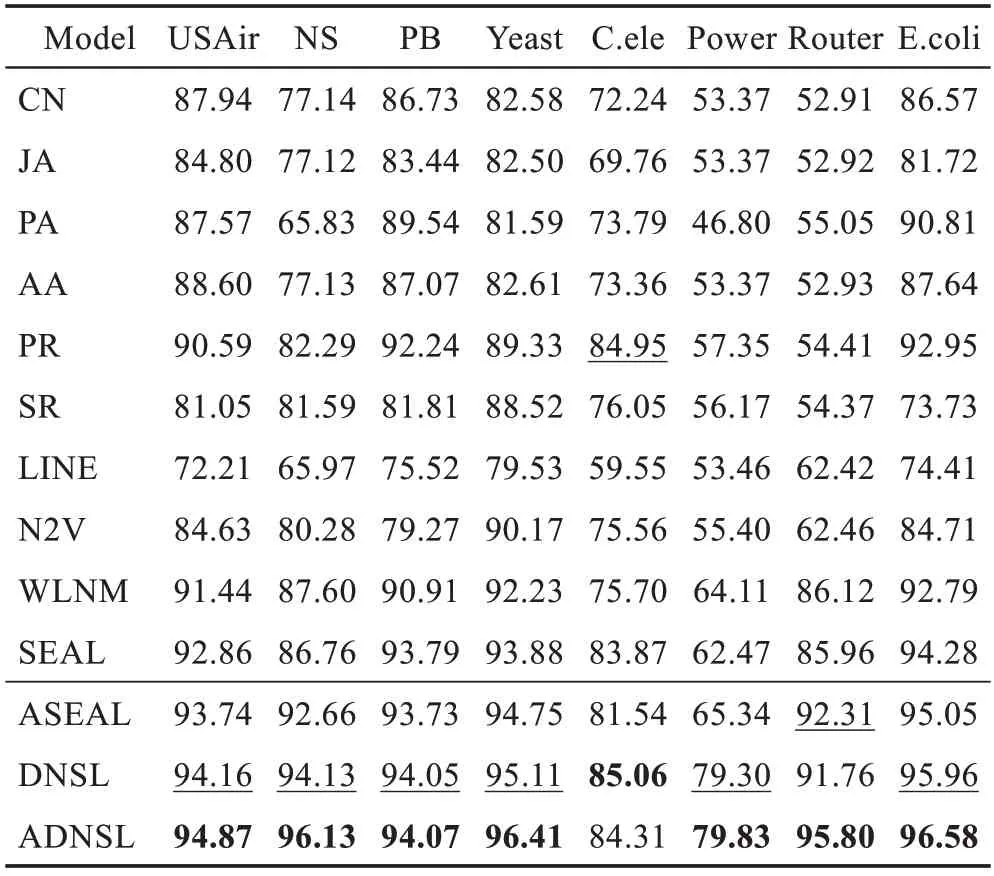
表2 模型AUC 對比（50%訓練鏈接）Table 2 AUC comparison of different approaches(50%training links) %

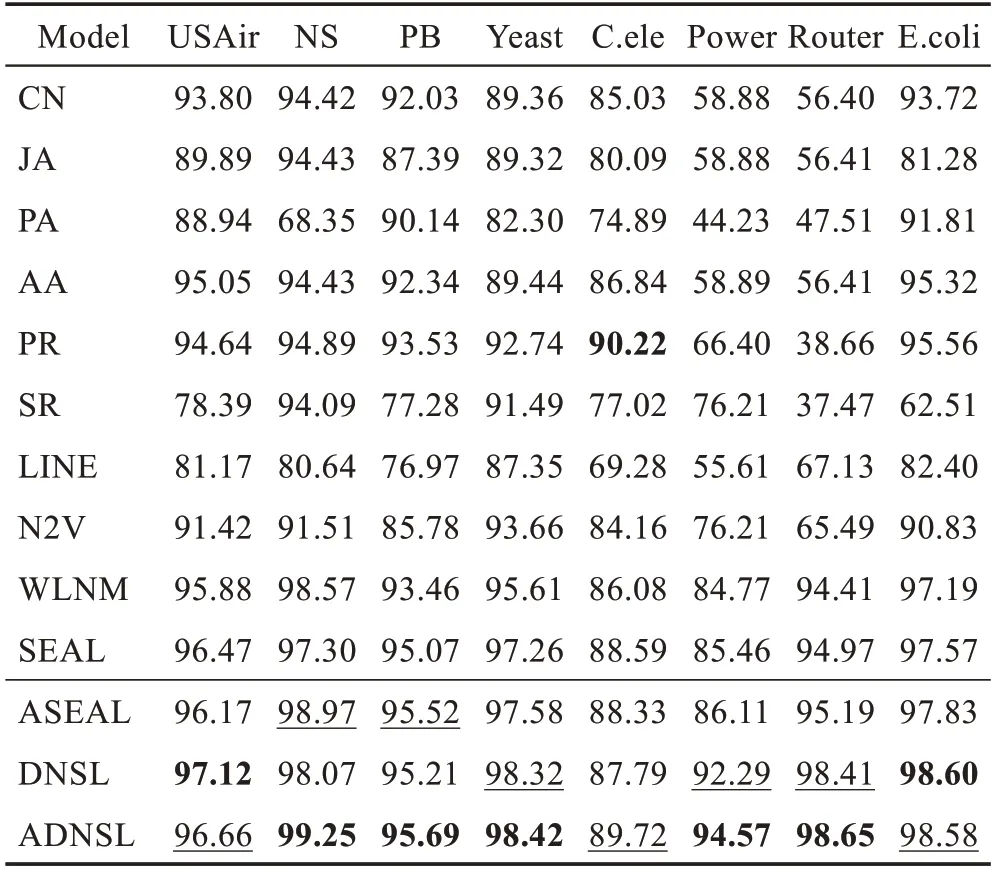
表3 模型AUC 對比（90%訓練鏈接）Table 3 AUC comparison of different approaches(90%training links) %

表中前六個方法為引言中提到的鏈接預測啟發式方法。

LINE 和N2V 為經典的節點嵌入算法，它們利用源節點周圍的節點信息生成向量表示，進而用于鏈接預測。

WLNM 算法利用目標鏈接局部子圖的節點標記重構鄰接矩陣，輸入全連接神經網絡鏈接預測。

SEAL 算法是表現十分優異的鏈接預測算法，利用圖神經網絡學習局部啟發式信息，進行端到端的鏈接預測。

ASEAL 是本文提出的結合雙向無參注意力機制的SEAL 算法鏈接預測模型。

DNSL 是本文提出的鏈接預測模型，其中圖卷積用于局部特征生成，struc2vec用于全局特征提取。

ADNSL 是本文提出的鏈接預測模型最終版本，結合多特征和圖注意力卷積，可以顯著提升鏈接預測的性能。

在八個數據集兩種情況下，結合表2 和表3，可以看出：

（1）ASEAL 相較于SEAL 有一定程度的性能提升，說明融合雙向無參注意力機制的圖卷積模型，可以在一定程度上彌補特征無效性和節點無偏性。

（2）DNSL 模型利用圖卷積作為局部特征生成模塊，struc2vec 作為全局特征提取模塊，可以有效結合局部和全局特征，很好地針對SEAL 的局部性獲得圖卷積部分無法學到的特征信息。

（3）ADNSL 模型相較于其他所有模型，均有非常顯著的性能提升。相較于SEAL，尤其對于NS、Power和Router這三個數據集，ADNSL 的提升尤為明顯，在表2 中AUC 值提升分別有10 個百分點、17 個百分點和10 個百分點左右。即使在表3 中，數據集中90%的邊作為訓練正例時，其他方法的AUC 表現良好，ADNSL 仍能有進一步提升。

對于NS、Power 和Router 提升十分明顯的原因，分析認為：ADNSL 等模型對于平均度較小的數據集，可以更好地捕捉式（7）所示節點度序列的差異，進而區分節點結構特征。例如，度為1 和2 的節點之間的距離為1，要遠遠大于度為101 和102 的節點之間的距離1/101。

圖7 為SEAL、ASEAL、DNSL 和ADNSL 四個模型在NS、Power 和Router 三個數據集，50%訓練鏈接情況下，訓練過程中LOSS 和ACC 值變化對比。

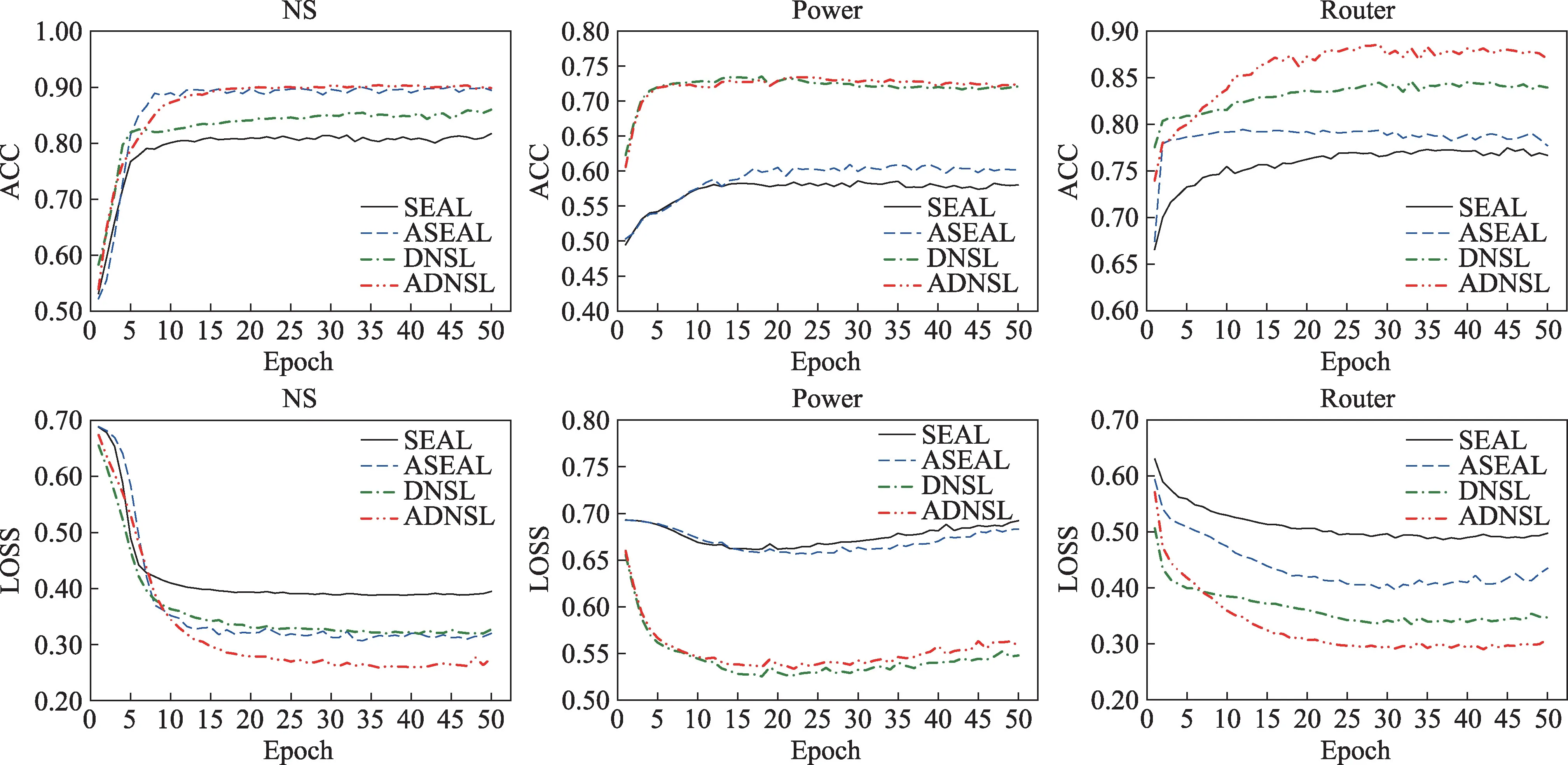
圖7 收斂性分析（50%訓練鏈接）Fig.7 Convergence analysis(50%training links)

可以很明顯地看出，相較于SEAL，本文提出的模型訓練起始值優于SEAL，且可以達到更優狀態。對于Power 數據集，次優模型SEAL 在訓練過程中的損失略有下降后，很快開始上升，而本文的模型可以較好地學習并達到穩定狀態。另外目前基于圖神經網絡的鏈接預測算法一般可以在50 輪以內達到最優值，而WLNM 等基于全連接神經網絡的算法往往需要100～150 輪才能得到穩定的結果。

3 結束語

在啟發式方法和節點嵌入算法研究的基礎上，利用神經網絡自動學習啟發式特征進行鏈接預測表現出優越的性能。本文在表現優異的算法SEAL 的基礎上，提出了融合圖注意力的多特征鏈接預測算法ADNSL。ADNSL 分為局部特征生成和全局特征提取兩個模塊，第一個模塊利用雙向無參注意力圖卷積學習啟發式特征，第二個模塊利用聚合圖提取目標節點的結構特征，然后將兩個模塊輸出的特征向量利用全連接層融合。

兩個模塊的特征融合可以有效解決基準算法SEAL 的局部性。圖注意力卷積中的雙向無參注意力可以在一定程度上彌補特征無效性和節點無偏性。利用迭代公式生成的聚合圖可以有效減少有偏隨機游走的時間，降低內存消耗和磁盤消耗。

實驗表明，本文提出的ADNSL 模型性能遠超傳統的啟發式算法，優于SEAL、WLNM 等表現優異的神經網絡算法。對于之前的工作中表現不理想的數據集，ADNSL 的表現有了巨大的提升。在未來的工作中，可以考慮更多更豐富的全局信息，例如社區信息（M-NMF、NECS 等）作為全局特征，進一步提高鏈接預測的性能。