基于電網熱紅外圖像增強算法質量評價

遲明偉

（哈爾濱新光光電科技有限公司，黑龍江 哈爾濱 150023）

紅外成像技術在軍事探測及民用生活等領域有著廣泛的應用。由于高位寬紅外探測器具有高精度、高靈敏度的特點，高動態范圍紅外圖像己成為紅外圖像發展的重要新方向。通常需要將高位的圖像數據壓縮至8位，以滿足普通顯示設備的正常顯示和圖像的后續快速處理，然而如果壓縮方法不當可能會造成原有信息丟失，在顯示圖像中表現為圖像細節的損失。因此，必須采取適當的壓縮方法保留圖像的細節，并使壓縮后的圖像細節顯示出增強的效果。

一般紅外成像系統可以由3部分組成：光學單元、紅外探測單元和圖像信號處理單元。紅外探測單元輸出的模擬信號一般為14 bit，動態范圍為16 384的原始紅外數據。但是，該數據需要經過數據映射和動態范圍壓縮[1-5]才可以在正常設備上顯示。在實際場景應用中，原始紅外圖像的動態范圍變化幅度較大，能夠連續穩定、保留邊緣和細節顯示在設備上[6-12]，并且對如何高效準確地通過圖像像素直接計算熱紅外設備對溫度的測量，和對動態范圍算法的設計都提出了較大的挑戰。

1 熱紅外圖像增強算法

1.1 線性映射濾波

在高動態紅外圖像，線性映射及其優化算法無法達到還原圖像作用的情況下，其根本原因在于線性映射單純將灰度范圍拉伸至最高精度范圍，沒有考慮各個灰度級所占比重。一般紅外圖像背景灰度較小、比重高，目標灰度大、比重小，若目標灰度比背景灰度大很多，背景中細節間較小的灰度差異就會體現不出來。直接對整張圖的各像素進行處理，實現比較簡單，復雜度也較低，但是圖像細節不夠凸顯。

F（x，y）為熱紅外原始數據，分別統計熱紅外原始數據最大值max和最小值min。

1.2 直方圖均衡化濾波

此方法是對圖像像素灰度級進行統計，這樣像素灰度級集中在某個范圍，對比度是由相鄰區域的像素差異決定的，所以通過此方法可以提高圖像的對比度。直方圖均衡化算法基于灰度直方圖的統計原理，其基本原理是根據像素點的個數重新分配灰度值，使直方圖灰度值根據像素點個數分布合理，實現圖像的非線性拉伸。在某些場景上效果不錯，但是缺點也很明顯，過度增強，噪聲過度放大，丟細節，褪色[13-16]。

計算偽代碼步驟：

第一步，統計熱紅外原始數據的直方圖分布；

第二步，計算熱紅外原始數據的分布頻率和累計分布頻率；

第三步，通過累計分布頻率乘以255，直接映射到8 bit。

1.3 導向濾波

很多傳統圖像濾波器與圖像內容之間是相互獨立的，濾波時對圖像內的所有像素都進行相同的運算，這常常會導致濾除噪聲的同時也抹去了圖像的細節，增強圖像細節的時候又增強了圖像噪聲[17]。為了使濾波器和圖像內容更好的結合，常用的有導向濾波和雙邊濾波，然而雙邊濾波可能會出現一些梯度反轉偽影。

計算偽代碼步驟：

輸入：輸入圖像p，導向圖I，區域半徑r，這里取值為3，正則化系數e，這里取值近似為0，f（mean）為半徑r的均值濾波器。

1.4 雙邊濾波

雙邊濾波可以保持細節信息又可以去噪，之所以達到這個效果，是因為雙邊濾波是由2個函數共同組成，一個函數可以通過幾何空間距離決定濾波的空域參數，而另一個函數可以通過像素的差決定濾波的值域參數。這2個函數提供了空域濾波以及值域濾波，也因為有這兩個濾波使得雙邊濾波器既能夠保留圖像邊緣又可以實現噪音的去除。雙邊濾波利用空域濾波，即高斯低通濾波器，以及值域濾波，即α-截尾均值濾波器：去掉百分率為α的最小值和最大之后剩下像素的均值作為濾波器，對圖像邊緣附近的像素進行濾波時，距離邊緣較遠的像素不會對邊緣上的像素影響太大，從而保證了圖像邊緣的清晰度。

雙邊濾波器在很多領域被應用，解決了邊緣保邊效果減弱，圖像不清晰問題，增強了圖像細節和層次感，在圖像研究中經常應用于平滑濾波和保邊。雙邊濾波保邊性會因為平滑濾波作用而減弱，造成圖像模糊不清晰[18-19]。

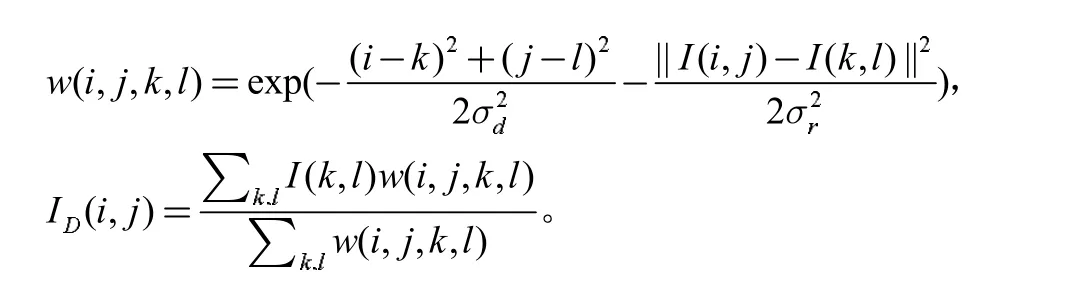
輸入I（i，j），輸出ID（x，y），σd和σr分別為歐式距離平滑系數和輻射差異平滑系數，取值分別為0.1和0.9。

1.5 高斯差分濾波

基于拉普拉斯高斯算子是現有數字圖像信號邊緣檢測算法中一種較好的方法，在圖像處理系統中得到廣泛應用。研究表明：在許多情況下，高斯差分濾波器DoG與拉普拉斯濾波LoG非常接近，復雜的LoG濾波可由DoG濾波以極高的精度逼近來實現。利用2個高斯核半徑值來描述2個高斯函數的差（Difference of Gaussian簡稱DoG）。可以看成從一個窄高斯減去一個寬高斯，利用高斯差分（DoG）帶通濾波提取背景不平度、光照不均等信息被有效提取出來[20-21]。

式中：x和y分別表示二維平面的橫、縱坐標；σ為二維高斯函數的方差，決定了二維高斯函數的空間分布。二維高斯函數在空間分布上呈現圓形對稱的單峰值形狀，σ越小，二維高斯函數在空間分布上越尖銳，變化越劇烈，其擴散面積越小；反之，σ越大，二維高斯函數在空間分布上越平滑，變化越緩慢，其擴散面積越大。對圖像用較大的高斯濾波器進行濾波，相當于對圖像做了平滑處理。輸入f（x，y），輸出DoG，高斯核半徑取值為30。

2 實驗與分析

觀察人員由于其自身喜好和經驗不同，評判同一幅圖像質量的好壞時會出現很大差異。因此，為了克服主觀人眼評價的不足，通常需要選擇一些實用的圖像質量客觀評價函數和標準，通過數據、數學模型或其他方式客觀地評價圖像處理結果的好壞，這樣也利于算法的選擇和優化。

通過本公司自研的熱紅外設備對變電站電網進行原始數據采集，分別利用以上5種熱紅外圖像增強算法對14 bit的原始數據進行8 bit數據映射，效果如圖1所示。

圖1 紅外圖像增強算法對比

2.1 信息容量

通過信息容量信息可以看出圖像的質量和信息豐富程度，本文使用二維直方圖來進行統計像素間的相關關系[22]。對于質量較好圖像的二維直方圖，在對角線區域內的頻數比周邊區域具有更高的幅度、分布密度和明顯的峰值，對于質量較差的二維直方圖則分布分散，沿對角線區域沒有明顯的峰值，相關性較差[23]。

從圖2可以看出高斯差分濾波相較于線性映射濾波、直方圖均衡化濾波、導向濾波、雙邊濾波有更高的幅值和分布密度。

圖2 信息容量比對

2.2 熵

根據傅里葉頻域分析理論，圖像的清晰程度主要由圖像分布的高頻分量的多少決定，高頻分量少則圖像模糊，高頻分量豐富則圖像清晰[24]。因此熵值越大，圖像越模糊，細節不明顯，反之，熵值越小，圖像邊緣和細節越明顯，圖像越清晰[25]。

從表1可以看出高斯差分濾波有較小的熵值，說明高斯差分濾波方法對處理14 bit熱紅外原始數據映射到8 bit圖像數據，可以最大保留圖像邊緣和紋理細節。

表1 5種紅外圖像增強算法熵值比較

2.3 時間復雜度

程序運行環境包括，軟件環境：vs2015，硬件環境cpu：Itel i5-2430，主頻：2.40 Ghz，內存：6 G。5種紅外圖像增強算法時間復雜度比較見表2。

表2 5種紅外圖像增強算法時間復雜度比較 單位：ms

3 結論

通過實驗分析了各自算法的優缺點，從信息容量、熵值和運行時間3個維度綜合比較。

根據上述結果可以看出，信息容量上線性映射濾波、直方圖均衡化濾波、導向濾波、雙邊濾波的二維直方圖對角線較分散，高斯差分濾的二維直方圖對角線較集中；熵值大小上線性映射濾波、直方圖均衡化濾波、導向濾波、雙邊濾波的熵值差別不大，高斯差分濾的熵值較小；時間復雜度上：線性映射濾波運行時間最短，雙邊濾波運行時間最長。