面向小樣本高維數據的秩檢驗非參控制圖

趙 宇 李艷婷

上海交通大學機械與動力工程學院，上海，200240

0 引言

統計過程控制(statistical process control，SPC)是利用數據對生產過程和產品質量進行監控的重要工具，也是貫徹實施全面質量管理的重要工具和質量保證手段。隨著大數據時代的到來以及數據感知和收集技術的成熟，質量數據向著多維度高頻次方向發展，多元統計過程控制(MSPC)成為了一個重要的研究問題。

隨著數據量的增加，不符合傳統正態性、低維度和樣本充足假設的數據越來越常見，例如：半導體制造企業通過傳感器技術實時收集和監控的工業生產中的關鍵質量指標維度超過500維[1]；生產過程穩定的電子元器件的壽命數據近似服從指數分布[2]；機械結構的疲勞壽命、磨損壽命、疲勞強度數據大多服從威布爾分布；供應商產品質量檢驗中常見的單側截尾的非正態數據和雙側截尾的非正態數據等；人造衛星、運載火箭、精密數控機床等產品受生產周期、實驗條件、研發成本等因素的限制，產量較少，收集到的數據十分有限；航空發動機中機匣轉子的碎片擊穿率評估、復合材料的許用值估計、武器射程評估等都屬于小樣本問題。

面向高維、非正態和小樣本數據的控制圖是當前多元統計過程控制研究的熱門方向。ZOU等[3]基于非參數似然比檢驗的方法設計了一個改進的非參數EWMA控制圖；李靜等[4]研究了控制圖參數k的動態更新和迭代，設計了監測過程方差微小波動的改進CUSUM控制圖；趙春華等[5]提出了一種基于融合特征約減的KPCA-SVM控制圖;BAE等[6]提出了一種基于數據深度的非參數多變量控制圖；HE等[7]運用了支持向量機監控多元過程的方法，提出了一種基于距離的控制圖。DENG等[8]基于實時對比的策略設計非參控制圖(記為RTC控制圖)；CHEN等[9]將Wilcoxon秩和檢驗與提出的多元經驗分布檢驗融合，設計出的EWMA控制圖對高維監控很有效(記為DFEWMA控制圖)；ZOU等[10]在多元符號檢驗的基礎上，設計了EWMA控制圖(記為SREWMA控制圖)；HAWKINS等[11]基于未知參數和已知參數的轉化設計了具有自啟動結構的EWMA控制圖(記為SSEWMA控制圖)；LI等[12]基于游程檢驗的雙樣本檢驗設計了在高維度大漂移情況下表現優異的多元非參數控制圖(記為HAMEWMA控制圖)。本文設計的HREWMA非參數控制圖在監測高維數據的大漂移時具有非常優異的表現，因此選擇上述在此條件下表現優異的多元非參控制圖進行對比。QIU[13]系統地分類并總結了非參數控制圖的研究進展。

針對變量相關性未知、分布未知、高維度等情況的數據監測問題，本文結合文獻[14]基于高維數據秩序的雙樣本檢驗，提出了基于高維數據秩序與EWMA結合的高維非參數控制圖(HREWMA)。通過馬爾可夫鏈的方法求解HREWMA控制圖的平均運行鏈長(ARL)，研究多種參數條件下控制圖ARL的表現。對比RTC控制圖[8]、DFEWMA控制圖[9]、SREWMA控制圖[10]、SSEWMA控制圖[11]、HAMEWMA控制圖[12]，證明在高維度小漂移的情況下HREWMA控制圖的表現更好。

1 基于高維秩檢驗的非參數控制圖

1.1 高維秩檢驗

假設Xij=(Xij1，Xij2，…，Xijp)T是相同且獨立分布的觀測值，i=1，2分別表示第1個、第2個樣本；j=1，2,…，ni，用n=n1+n2表示總樣本量，其中，n1、n2分別為樣本1與樣本2的樣本量。N=p(n1+n2)是總樣本量n對應的p個維度的全部觀測值。

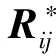
(1)

1≤rijk≤n

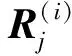
(2)

定義邊際分布函數的平均值為

定義漸近秩變換為

Yij=(Yij1，Yij2，…，Yijp)T

Yijk=H(Xijk)

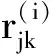
(3)

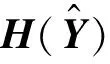
(4)

u∈[0,n1]v∈[1,n1]u∈Nv∈N

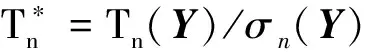
(5)

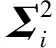
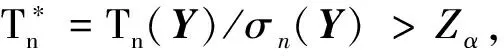
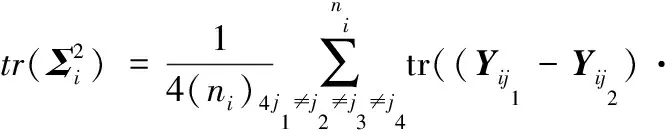
(6)

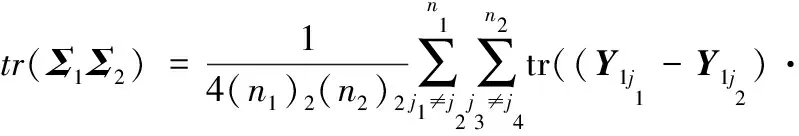
(7)

(ni)k=ni!/(ni-k)!

j1∈[1,ni]j2∈[1,ni]j3∈[1,ni]

j4∈[1,ni]j1,j2,j3,j4∈N

經過文獻[14]改進的檢驗統計量的第一類錯誤概率更低，并且該檢驗統計量更適用于非參數假設，因此本文采用文獻[14]提出的檢驗統計量進行EWMA控制圖的設計。

1.2 多元非參數控制圖HREWMA

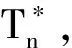
本文秩檢驗的方法過程均值偏移的方向是已知的(向上漂移)，采用傳統的雙邊EWMA控制圖監控過程的效果并不理想，為了充分利用過程均值的方向信息，采用單邊EWMA控制圖來監控過程。設定單邊EWMA控制圖的統計量為

(8)

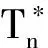
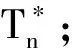
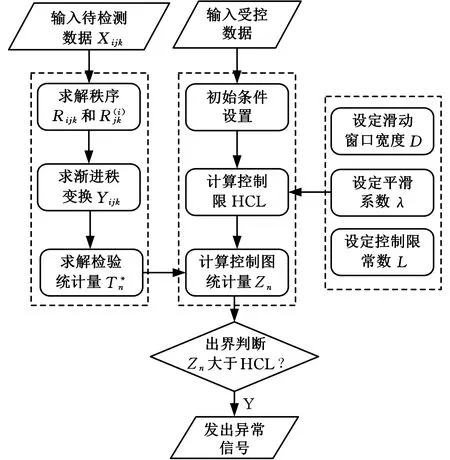
圖1 HREWMA控制圖的監控過程Fig.1 The monitoring process of HREWMA control chart

計算HREWMA控制圖平均運行鏈長的方法如下：

(1)設定平滑系數λ和滑動窗口D的值；

(2)設定控制限常數L并計算控制圖的控制限(n表示所計算樣本的數據量)：

(9)

(3)設定HREWMA控制圖檢驗統計量初始值Z0=0；

(4)根據式(8)求得Zn；

(5)通過馬爾可夫鏈求解受控狀態下的平均運行鏈長ARL，然后通過蒙特卡羅隨機模擬法求解失控狀態下的ARL。

1.3 HREWMA檢驗統計量計算的程序加速方法

針對本文檢驗統計量的計算，采用常規的計算方法將耗費大量的時間，因此，針對本文檢驗統計量的計算，尤其是針對比率一致估計σn的計算，給出以下程序加速建議。

1.3.1減少重復計算項

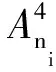
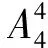
基于該程序加速規則，使用該方法的理論程序運行時間減少至未使用該加速方法的1/8。對于一個受控樣本量m0=50、滑動窗口D=10、數據維度p=10的HREWMA控制圖，使用該加速方法與未使用該加速方法相比，計算量從105數量級減小至104數量級。

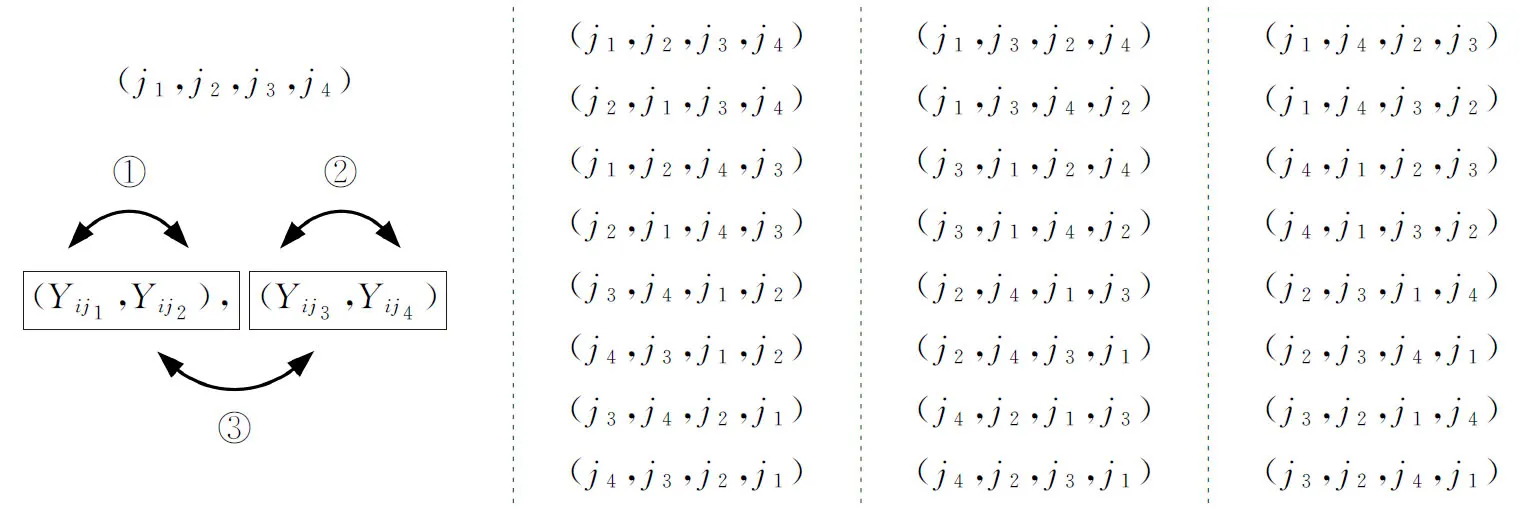
圖2 檢驗統計量加速方法：減少重復項

1.3.2矩陣跡的加速計算

在計算式(6)時，涉及到兩方陣相乘后取矩陣的跡的計算，采用常規的計算方法，需要先將兩個方陣相乘后的矩陣求出，再將矩陣的對角線元素相加取跡。基于圖3所示的計算方法，可以減少矩陣中行列相乘的計算次數，加快程序速度。

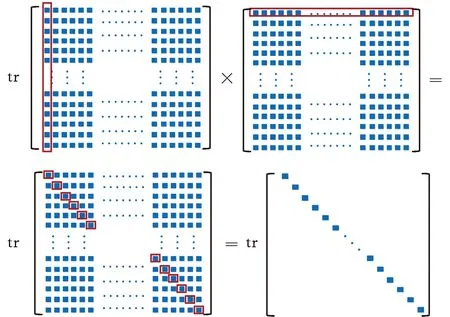
圖3 檢驗統計量加速方法：矩陣跡的加速計算Fig.3 Test statistics acceleration method:acceleratedcalculation of matrix trace

基于該程序加速規則，使用該方法的理論程序運行時間減少至未使用該加速方法的1/p。對于一個受控樣本量m0=50、滑動窗口D=10、數據維度p=10的HREWMA控制圖，使用該加速方法與未使用該加速方法相比，將計算量從104數量級減小至103數量級，程序運行時間減少至未使用該加速方法的1/10。

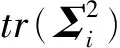
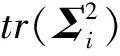
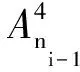
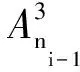
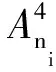
基于該程序加速規則，使用該方法的理論程序運行時間減少至未使用該加速方法的4/m0。對于一個m0=50、D=10、p=10的HREWMA控制圖，使用該加速方法與未使用該加速方法相比，將計算量從103數量級減小至102數量級，程序運行時間減少至未使用該加速方法的2/25。

1.4 HREWMA控制圖平均運行鏈長的計算

平均運行鏈長(ARL)表示從檢測開始直到控制圖發出警報所抽取的平均樣本數量。當過程是受控的，為了避免誤報情況的發生，希望ARL越大越好；當過程是失控的，希望控制圖可以盡快報警，希望失控的ARL盡可能小。在比較不同控制圖的性能時，ARL是不容忽視的指標。控制圖ARL的計算方法有：蒙特卡羅隨機模擬法、積分法和馬氏鏈法。本文采用馬氏鏈法計算HREWMA控制圖的平均運行鏈長。

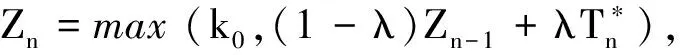
首先，對HREWMA控制圖進行區間劃分。將控制限區間[t0，LHCL]劃分成t個子區間，每個子區間的寬度為d=(LHCL-k0)/t，此時HREWMA控制圖的統計量Zn在控制限區間[t0，LHCL]的變化過程可以看作具有(t+2)個狀態的馬爾可夫鏈轉移問題。

然后，定義每個區間的狀態Sn，n=1，2，…,k，統計量Zn處于狀態Sn的條件可以表示為

LHCL-nd≤Zn≤LHCL-(n-1)dn=1，2，…k

最后，構造出HREWMA控制圖的狀態轉移概率矩陣

(10)

其中，pi，j代表統計量Zn從狀態Si轉移到狀態Sj的概率。

綜上可知，P是t+1階方陣，最后一行(0，0，…，0，1)代表從吸收狀態St+1到轉移狀態Si的概率，最后一列(v1，v2，…，vt，1)T代表從轉移狀態Si到吸收狀態St+1的概率。可以看到，ARL的取值只受前t行的影響，因此對一步轉移概率矩陣進行分塊：

(11)

其中，R矩陣是將P矩陣去掉最后一行和最后一列得到的t階矩陣，I是t階單位矩陣，1是一個元素全是1的t×1列向量，0是一個元素全是0的t×1列向量。

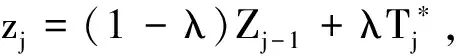
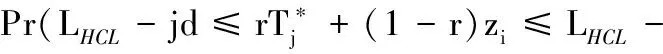
(12)

根據馬爾可夫鏈的性質可得，第i步轉移概率矩陣Pi可以表示為

(13)

因此鏈長LRL=i的概率：

Pr(LRL=i)=Pini(Ri-1-Ri)1

(14)

因此平均運行鏈長ARL可以表示為

(15)

2 仿真檢驗

HREWMA控制圖的優勢在于對高維度、大漂移數據的檢測，所以選擇此狀況下具有優異表現的多元非參數控制圖作對比：RTC控制圖[8]，DFEWMA控制圖[9]，SREWMA控制圖[10]，SSEWMA控制圖[11]，HAMEWMA控制圖[12]。

2.1 仿真參數設定

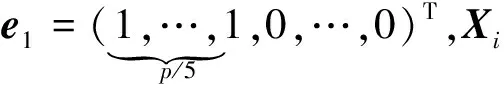
(1)HREWMA控制圖平滑系數λ，分別取值0.05和0.1；

(2)受控樣本數量m0分別取值50，60，70，80，90；

(3)受控樣本和待檢測樣本的維度p分別取值10，20，30，40，50；

(4)均值漂移量δ分別取值0.5，1，2，4；

(5)滑動窗口寬度D分別取值10，20，30，40，50；

(6)檢測數據的分布考慮以下3種分布類型：①多元正態分布，記作Normp；②多元t分布，自由度是ξ，記作tp，ξ，其中ξ=5；③多元Gamma分布，形狀參數φ，尺寸參數是1，記作Gamp，φ，其中φ=3。

2.2 仿真結果

運用馬爾可夫鏈得到HREWMA控制圖受控狀態的平均運行鏈長，記為IC ARL(ARL受控); 因為無法估計失控狀態下檢驗統計量的分布情況，故通過蒙特卡羅隨機模擬法求解HREWMA控制圖失控狀態的平均運行鏈長，記為OC ARL(ARL失控)。在IC ARL相同的設定下，比較不同控制圖OC ARL的大小，OC ARL越小，說明控制圖的性能更好。

2.2.1受控過程分析(ICARL)

在初始受控平均運行鏈長200的設定下，對比HREWMA控制圖與一些代表性的多元非參數控制圖(HAMEWMA、SREWMA、DFEWMA、SSEWMA、MSEWMA、MEWMA、RTC)在受控數據監測中的平均運行鏈長(IC ARL)，結果如表1所示。

由表1可知，HREWMA控制圖的IC ARL大致在200左右，并且標準差也大致為200。表中的MSEWMA、MEWMA、RTC控制圖的ICARL顯著低于預期設定值，在實際的監控過程中會頻繁報警，在受控狀態下HREWMA控制圖的監控效果比較穩定。

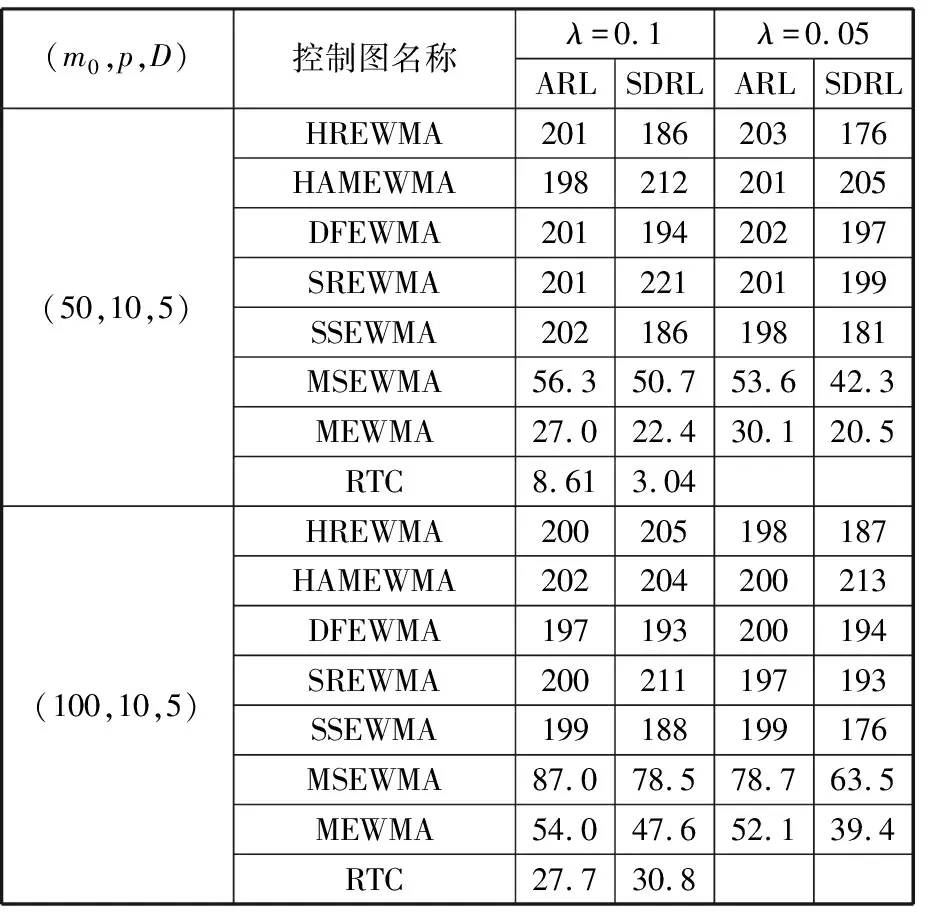
表1 控制圖表現對比(IC ARL)

2.2.2失控過程分析(OCARL)

在不同分布類型、漂移量、滑動窗口寬度、數據維度、平滑系數及受控樣本量的條件下，各個控制圖在失控狀態下的表現情況如下。

(1)滑動窗口的影響。由圖5可知，隨著滑動窗口的增大，3種分布的OC ARL均逐漸減小，其中，多元t分布的OC ARL減小的程度更加明顯，說明滑動窗口寬度越大，HREWMA控制圖的控制效果越好。

(2)數據維度的影響。由圖6可知，對于多元正態分布、多元t分布、多元Gamma分布，隨著數據維度的增大，OC ARL逐漸減小，數據維度越高，HREWMA控制圖的控制效果越好，因此HREWMA控制圖處理高維數據時有更好的表現。

(3)受控樣本量的影響。由圖7可知，隨著受控樣本量的增大，3種分布的OC ARL均逐漸減小，但是減小程度明顯小于滑動窗口和數據維度的影響，證明HREWMA控制圖不需要過高的受控樣本量。

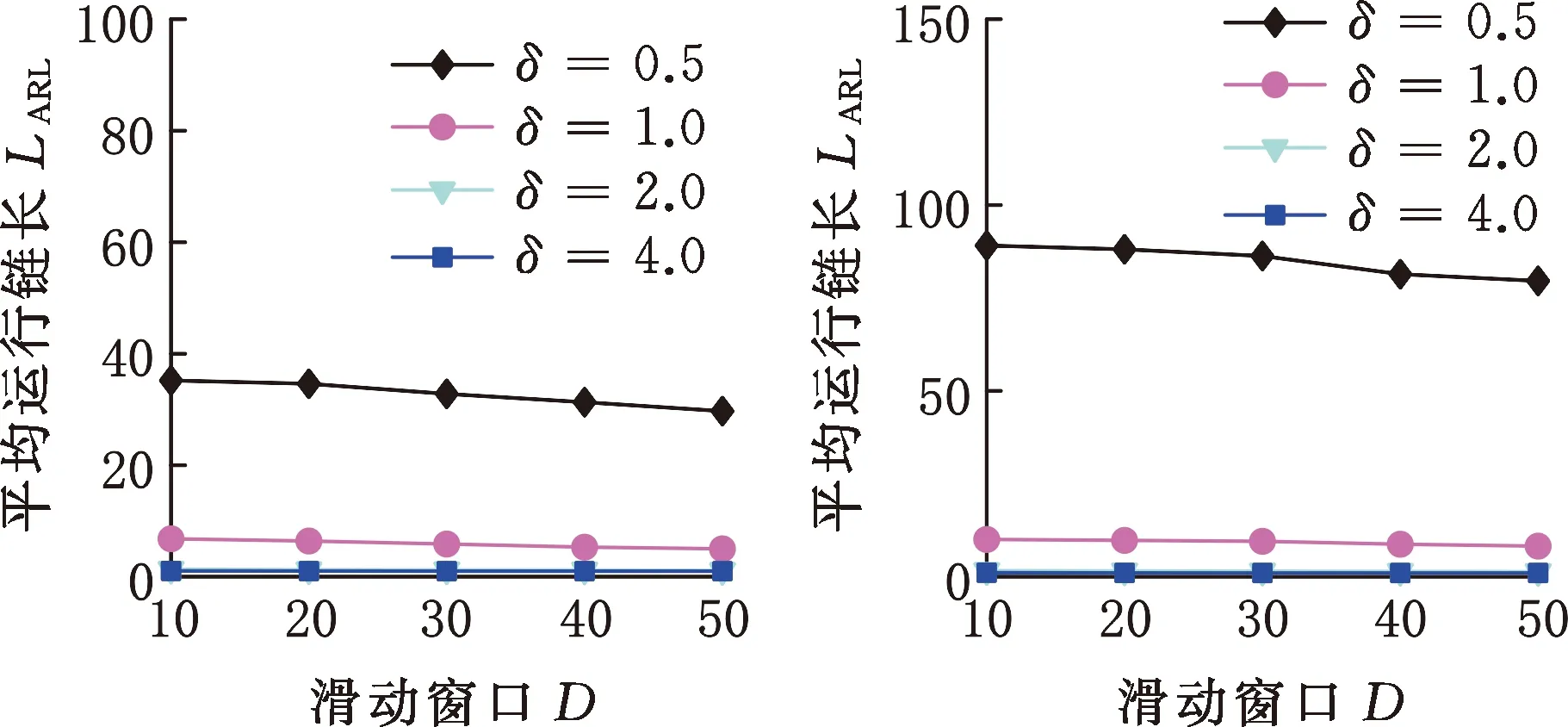
(a)Norm10 (b)t10，5

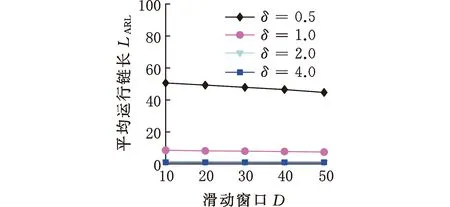
(c)Gam10，m3圖5 HREWMA控制圖在不同滑動窗口下的OC ARL比較Fig.5 Comparison of OC ARL of HREWMA controlchart under different sliding windows

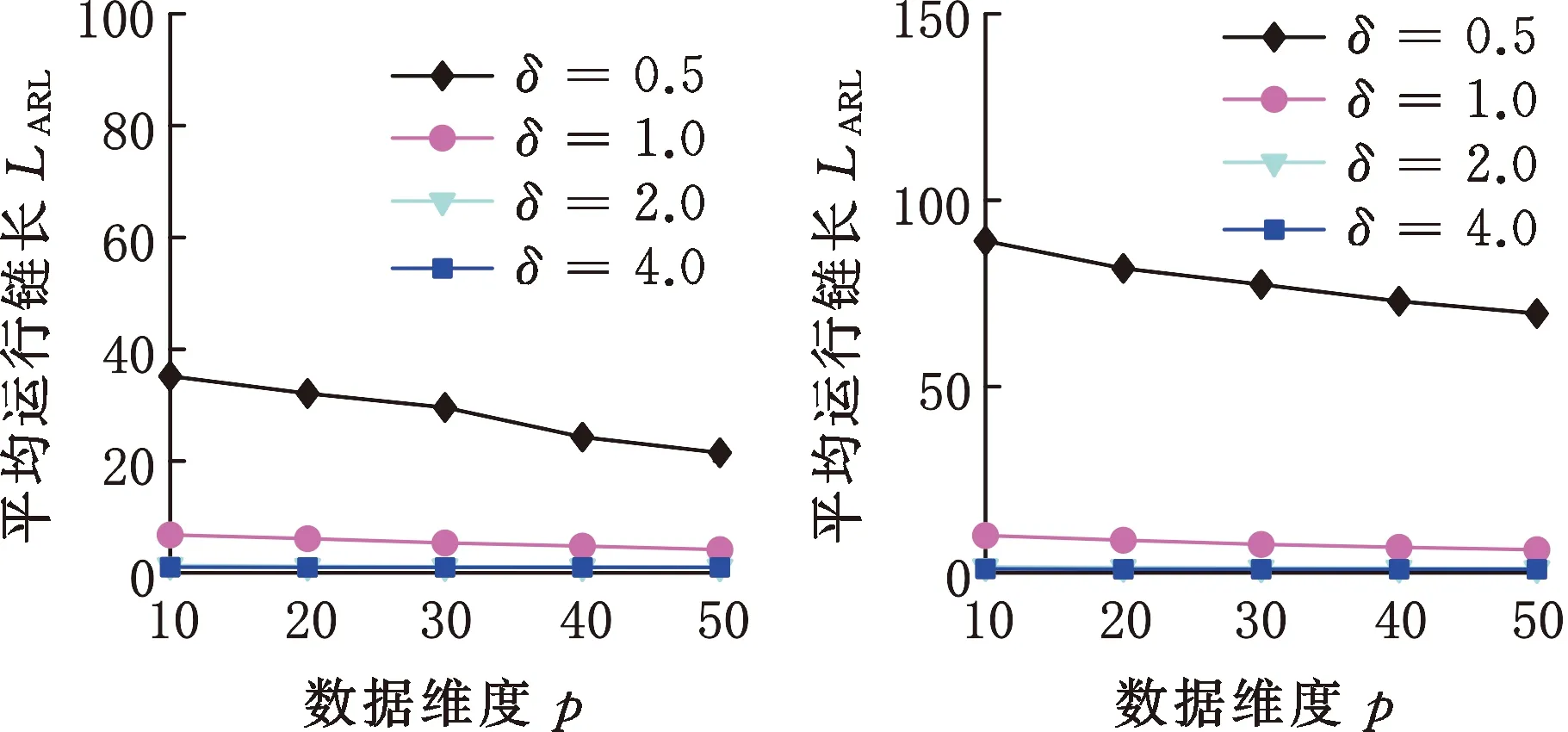
(a)Norm10 (b)t10，m5

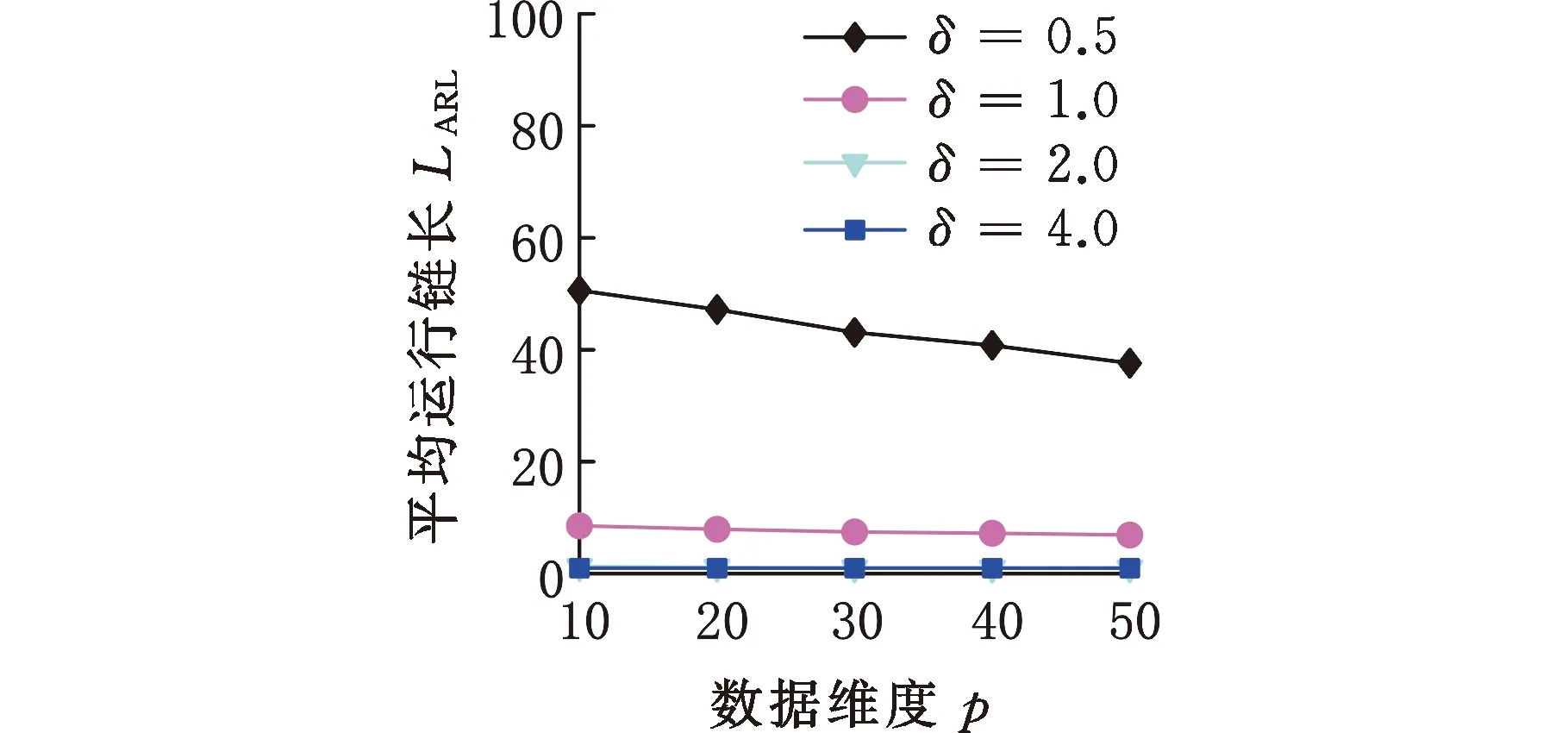
(c)Gam10,3圖6 HREWMA控制圖在不同維度下的OC ARL比較Fig.6 Comparison of OC ARL of HREWMA controlchart in different dimensions

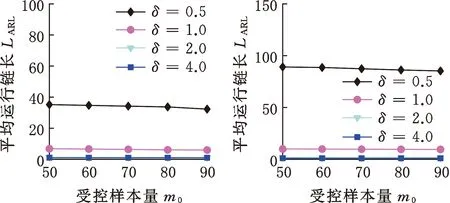
(a)Norm10 (b)t10,5

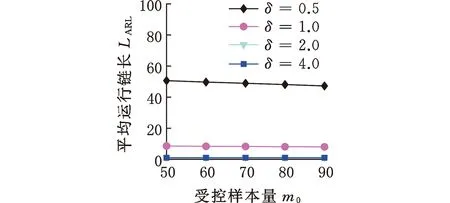
(c)Gam10,3圖7 HREWMA控制圖在不同受控樣本量下的OC ARL比較Fig.7 Comparison of OC ARL of HREWMA controlchart under different controlled sample sizes

(4)漂移量的影響。由圖8可知，隨著漂移量的增大，3種分布的OC ARL均逐漸減小，尤其是HREWMA控制圖在大漂移時具有很好的監控效果。

2.3 仿真結果討論

結合表2、表3以及圖8中HREWMA與其他控制圖的比較，詳述仿真的6個因素對HREWMA控制圖監控效果的影響。

(1)平滑系數。對比發現，DFEWMA、SREWMA、SSEWMA控制圖在平滑系數λ=0.05時對小漂移控制效果不佳，HREWMA控制圖在λ=0.05時對小漂移有較好的控制效果。因此當平滑系數較小時HREWMA控制圖同樣具有良好的監控效果。

(2)樣本量。當受控樣本在50和90之間變化時，監控效果較為穩定，因此推斷樣本量增至50以上，監控效果較好且基本不受樣本量的影響。

(3)滑動窗口。隨著滑動窗口的增大，3種分布的監控效果均有更優的表現。其中多元t分布下，大的滑動窗口監控效果更好。

(4)數據維度。數據維度越大，HREWMA控制圖的監控效果越，因此推斷HREWMA適用于高維數據的檢測。

(5)漂移量。與其他多元非參數控制圖對比發現，HREWMA控制圖在小漂移與大漂移的情況下均有較好的監控效果，其中對大漂移的監控效果極佳，在參與對比的控制圖中達到最優水平。

(6)分布類型。HREWMA控制圖在3種分布中均有較好的控制效果，對多元正態分布和多元Gamma分布有更優的監控效果。因此，HREWMA控制圖具有普適性，能夠有效監控分布未知的數據，并且推測對于多元正態分布和多元Gamma分布的數據具有較突出的表現。

3 實例分析

3.1 控制圖在半導體生產中的應用

為了用高維數據集驗證HREWMA控制圖的性能，本文選取來自于MICHAEL[17]的數據集SECOM，記錄了2008年7月至2008年10月通過半導體生產過程中的測量點的傳感器收集得到的數據。共收集了1567個半導體產品的591維質量數據，得到的數據匯總為一個1567×591的矩陣。每個產品有分類標簽，將該產品區分為合格樣本和缺陷樣本(±1)。在該數據集中合格品的樣本量是1463個，不合格品的樣本量為104個。挖掘龐大的高維數據，可以獲得諸如產品質量特性分布、產品質量特性的變化趨勢、質量特性之間的相關關系等信息。對數據進行正態性檢驗，根據圖9中的QQ圖和直方圖，在不同維度下數據分布并非滿足正態性假設，運用傳統的基于正態性假設的控制圖對SECOM數據進行檢測，不能得到可靠的監控效果。

(a)Norm10(λ=0.05) (b)t10,5(λ=0.05) (c)Gam10,3(λ=0.05)

(d)Norm10(λ=0.1) (e)t10,5(λ=0.1) (f)Gam10,3(λ=0.1)圖8 當λ=0.05/0.1、m0=50、維度p=10時控制圖對比(OC ARL)Fig.8 Comparison of control charts when λ=0.05/0.1，m0=50 and dimension p=10(OC ARL)

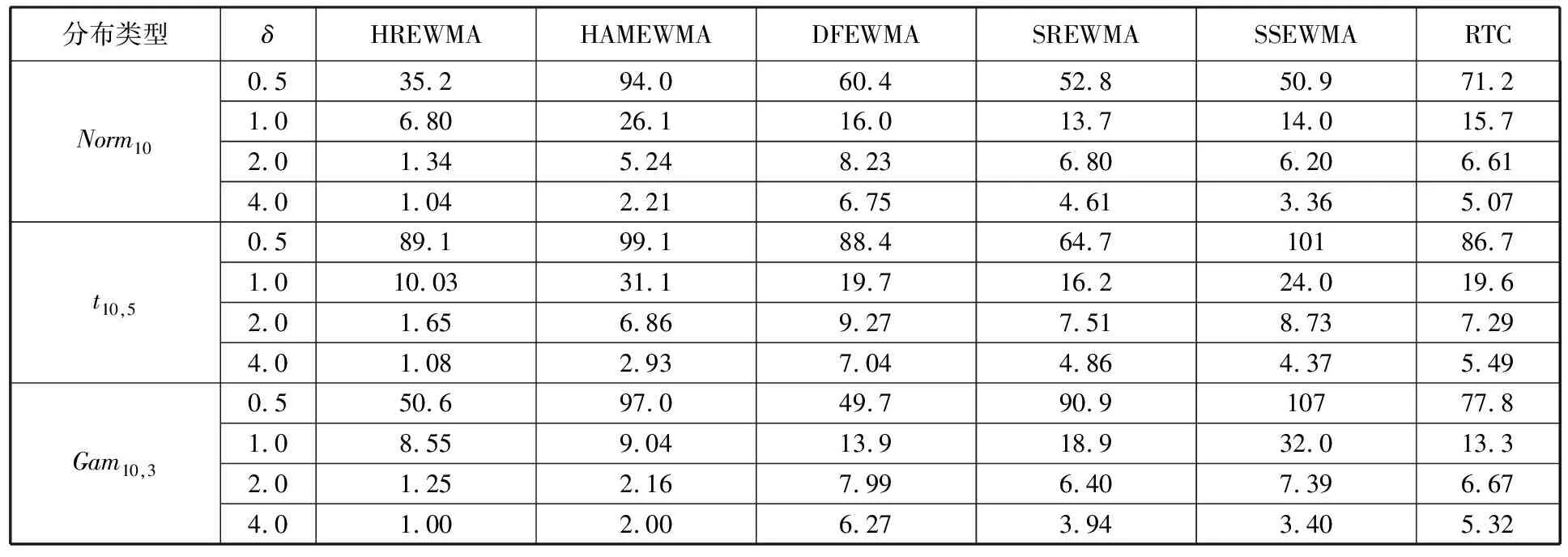
表2 當λ=0.05、m0=50、維度p=10時控制圖OC ARL對比

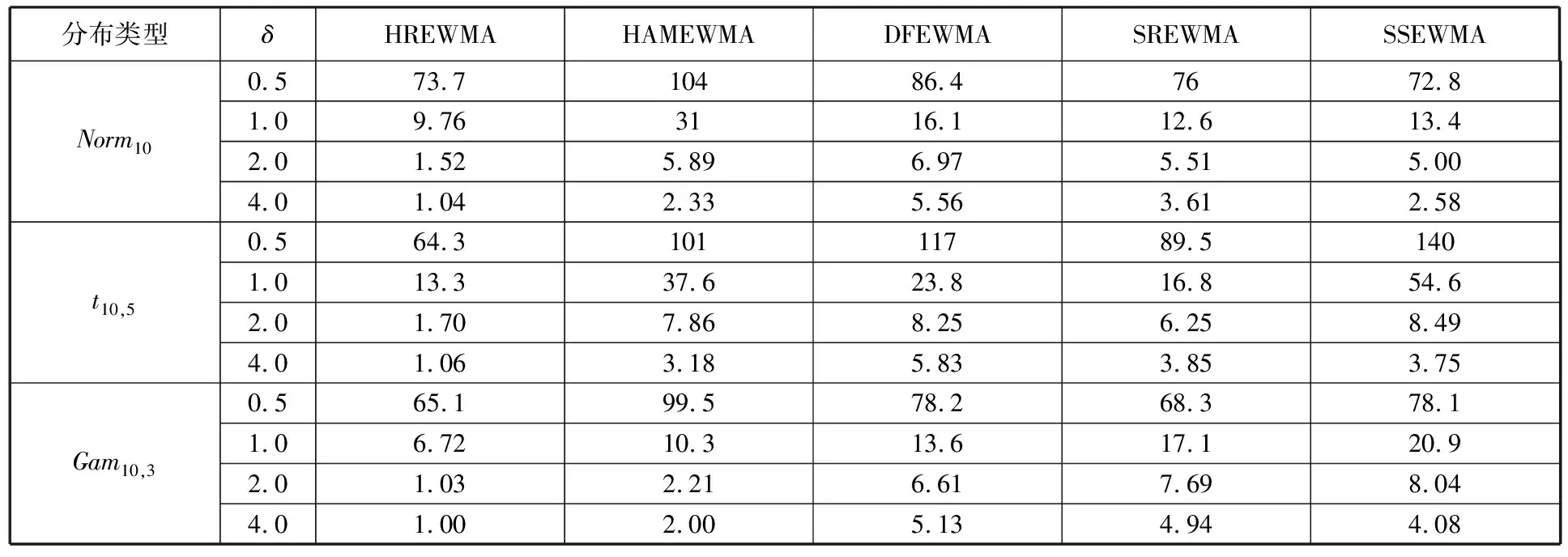
表3 當λ=0.1、m0=50、維度p=10時控制圖OC ARL對比

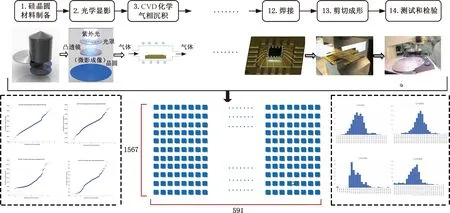
圖9 半導體制造中高維數據的產生Fig.9 The generation of high-dimensional data in semiconductor manufacturing

運用HREWMA控制圖對數據進行監控。在合格樣本數據集中隨機選取m0=50作為受控樣本，控制圖基本參數設置為LARL0=200，λ=0.05，D=10。首先根據控制圖參數的設置利用受控數據集得到控制限，待監測樣本由隨機選取的15個合格樣本數據和85個不合格樣本數據組成，得到控制圖見圖10。在第17個數據時控制圖判斷數據異常并報警。

將HREWMA控制圖在SECOM數據集上的運行結果與其他非參數控制圖在SECOM數據集上的運行結果進行對比。LI等[12]提出的HAMEWMA控制圖在含變點的SECOM數據集上(由15個受控樣本和85個不合格樣本數據組成)進行數據監控，在第25個數據時判定異常數據加入，控制圖報警。CHEN等[9]提出的 DFEWMA控制圖監控含變點的SECOM數據集(由63個受控樣本和37個不合格樣本數據組成)，在第71個數據點時控制圖判定異常并且報警。與其他在SECOM數據集上進行監控的非參數控制圖對比發現，本文提出的HREWMA控制圖對異常數據的加入更敏感，控制圖報警更快速，監控效果更佳。

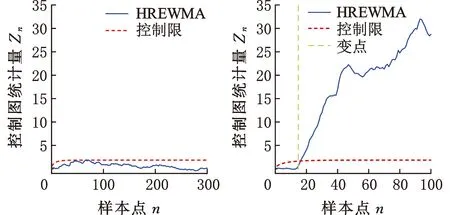
(a)受控的SECOM數據(b)含變點的SECOM數據

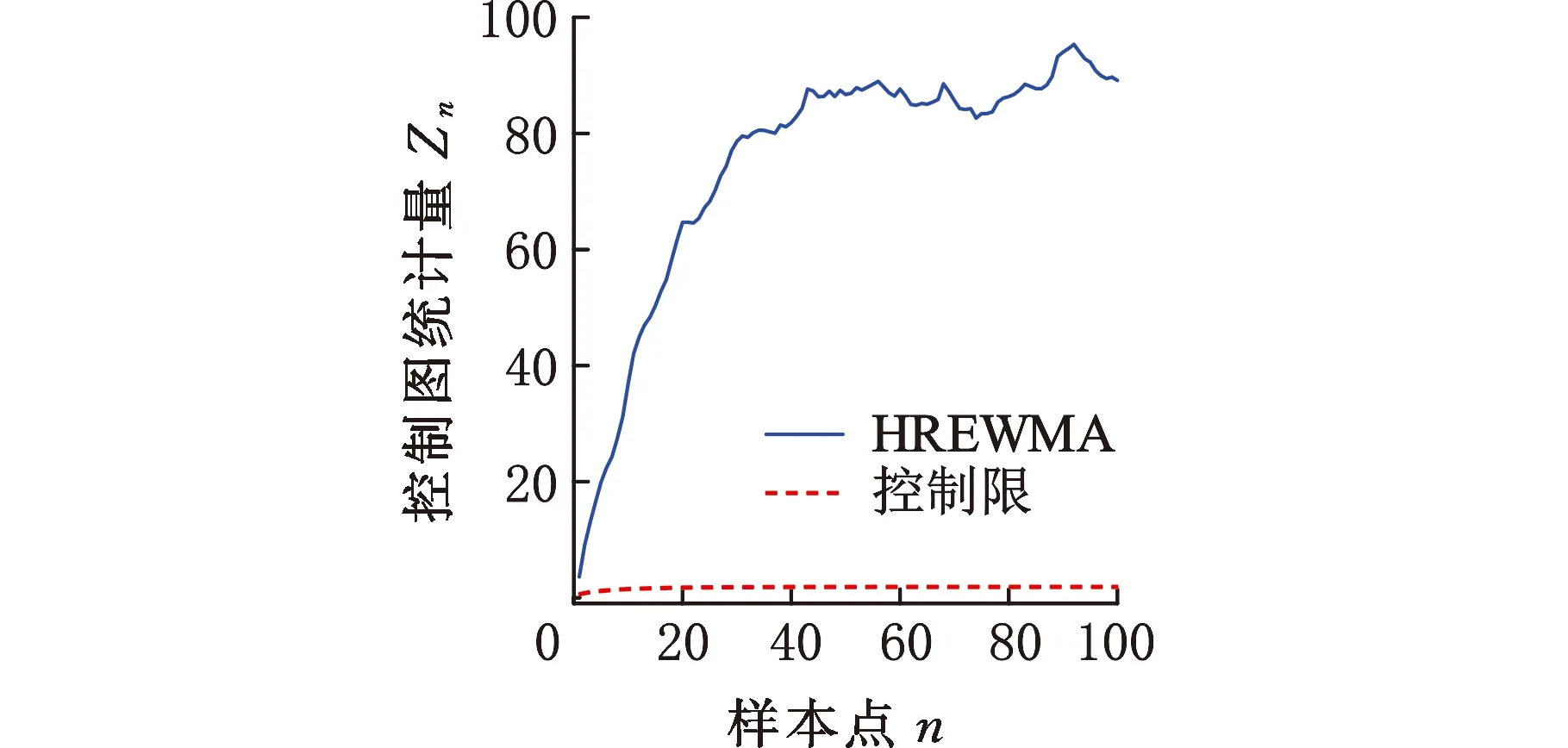
(c)失控的SECOM數據圖10 HREWMA在受控、含變點、失控SECOM數據的監控效果Fig.10 Monitoring effect of HREWMA on SECOM dataunder control, including change points, and out of control

3.2 控制圖在白葡萄酒生產中的應用

本文采用白葡萄酒生產中的高維數據來證明HAMEWMA控制圖的實用性。白葡萄酒數據集(Wine Quality數據集)由CORTEZ等[18]提供，從UCI機器學習的資料庫[17]中獲取。數據集的時間區間為2004年3月至2007年2月，由生產白葡萄酒的自動化系統在多個采樣點收集得到。白葡萄酒數據集由11個連續變量與1個分類變量組成，共包含4898個樣本點。其中，11個連續變量表征白葡萄酒的性質，分別為：游離二氧化硫、總二氧化硫、密度、檸檬酸、揮發性酸度、固定酸度、硫酸鹽、酒精度、殘糖、氯化物、pH值。1個分變量表征白葡萄酒的質量，共包含從LV0(極差)到LV10(極好)的11個等級。

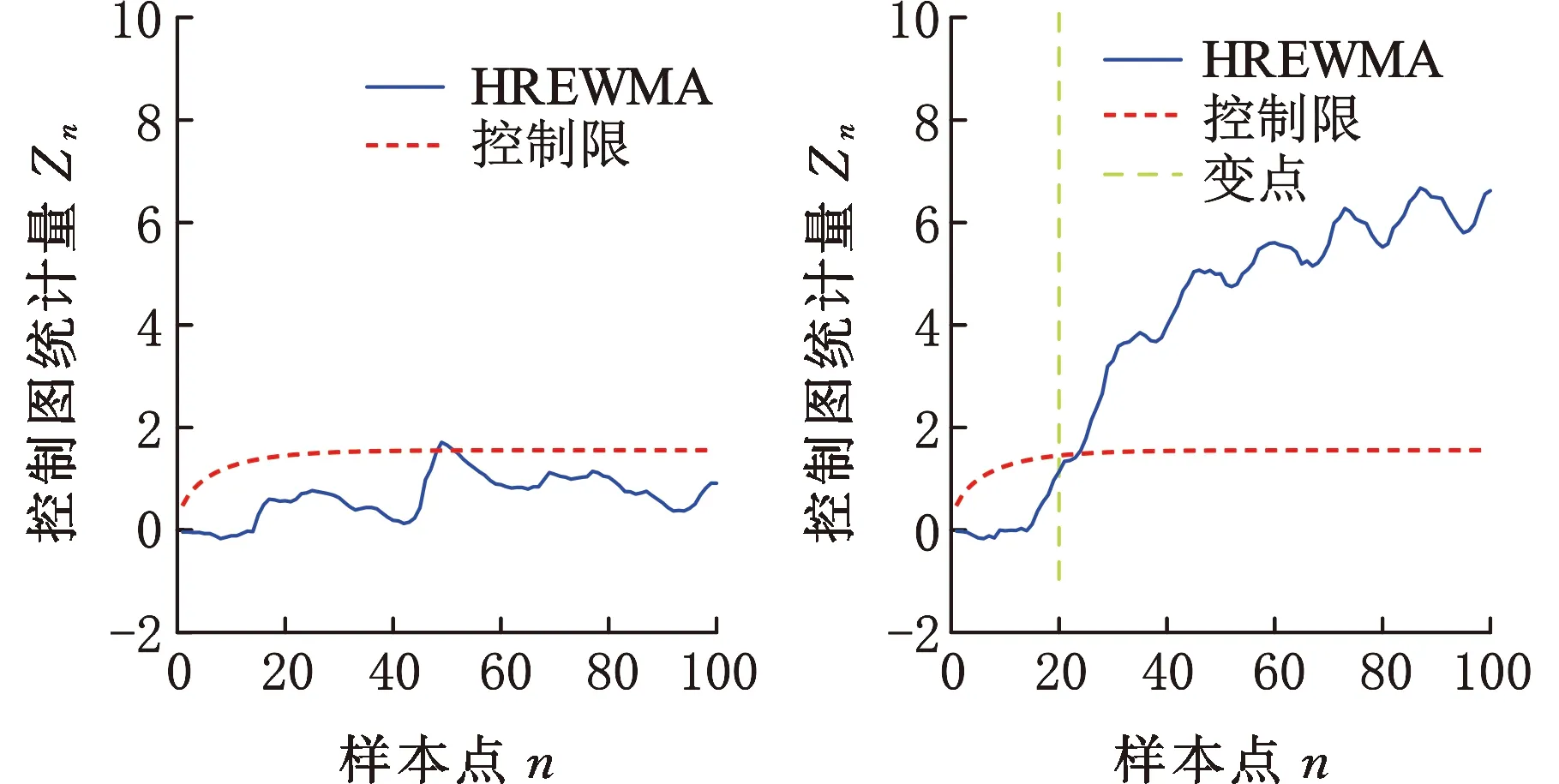
(a)受控的Wine Quality數據(b)含變點的Wine Quality數據

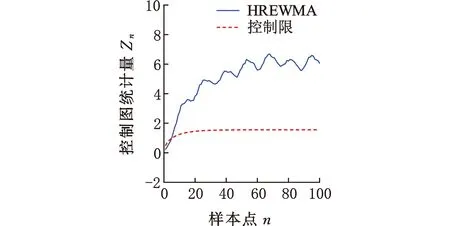
(c)失控的Wine Quality數據圖11 HREWMA在受控、含變點、失控Wine Quality數據的監控效果Fig.11 Monitoring effect of HREWMA on WineQuality data under control, including change points,and out of control

依據HREWMA控制圖對Wine Quality數據集進行監控，從LV7的數據中取m0=20個樣本作為受控樣本。設置控制圖的基本參數LARL0=200，λ=0.05，D=10，根據仿真得到HREWMA控制圖的控制限。按照順序從LV7的數據集中隨機抽取20個樣本，從LV6的數據集中抽取80個樣本，得到HREWMA控制圖的監控效果如圖11所示。在第25個數據點時控制圖判斷數據異常并且報警。ZOU等[10]在含有變點的Wine Quality數據集(由30個從LV7中選取的受控數據和70個從LV6中選取的不合格數據組成)上進行監控，在第55個數據點時控制圖報警。與ZOU等[10]提出的SREWMA控制圖相比，HREWMA控制圖具有更好的監控效果，實用性更強。

4 結語

針對一些工業生產中存在的高維度、未知分布、受控樣本小的數據特性，本文基于雙樣本高維秩檢驗設計了多元非參數HREWMA控制圖,通過仿真分析和實例檢驗，證明HREWMA控制圖具有更好的監控效果；并且通過與其他控制圖的對比，證明HREWMA控制圖對高維、小樣本數據具有更好的表現；此外，HREWMA控制圖在非正態數據中依然有良好的監控效果。與傳統的多元非參數控制圖比較發現，HREWMA控制圖具有較好的監控效果，可以運用到實際生產控制中。