扁平形聚酯纖維Dclany-Bazlcy吸聲模型的優化方法
何宇辰,胡 晨,王俊杰,姚智敏,蔡 俊
(1. 國網安徽省電力有限公司經濟技術研究院,安徽合肥 230022;2. 上海交通大學環境科學與工程學院,上海 200240)
0 引 言
纖維材料以其在中高頻段具有良好的吸聲效果而被廣泛應用于航天航空、建筑、汽車等減震降噪領域,受到了國內外學者們的高度關注[1]。由于纖維材料種類繁多,通過理論模型對不同類型纖維的吸聲材料進行參數優化及性能預測,不僅可以節約研發成本,還可以根據實際需求進行材料開發以及相關降噪措施的快速實施,對噪聲污染控制新材料和新技術的研發意義重大[2]。
為了準確預測纖維材料的吸聲系數,研究人員建立了各種吸聲模型。其中最具代表性的是Dclany-Bazlcy (DB)模型[3]。由于簡單便捷,該模型從20世紀70年代開始一直被廣泛應用于纖維多孔性材料的吸聲特性研究。由于該模型所涉及的參數較少,導致預測結果與實際數值之間容易存在較大的差異。為此,多年來DB模型被眾多學者延伸拓展,以期擴大應用范圍,提高模型預測的準確性。Miki[4]修正了 DB模型阻抗的正實數特性,使模型能在更寬的頻率下得到了更好的運用,特別是在低于400 Hz的頻率范圍。Garai等[5]通過對不同直徑(18~48 μm)的聚酯纖維材料進行測量,提出了更適合紡織纖維的相關系數。Takcshi[6]基于快速傅里葉轉換法進一步改進了DB模型,分別建立了玻璃棉和巖棉的吸聲經驗模型,實驗證明改進的模型在一定頻率下的預測結果比原模型更接近實測值。但這些研究僅針對常規截面(圓形截面)纖維,而對于異形截面纖維的吸聲系數預測模型研究未見報道。
在纖維的實際運用中,常規圓形截面的纖維技術工藝相對成熟,性能穩定,但是具有易沾污、易起球和易鉤絲等缺點。而有研究表明,異形截面的纖維不但能克服上述問題[7],而且因其擁有更大的比表面積而具有更良好的吸聲性能[8-11]。但目前還沒有適合異形截面纖維吸聲性能的預測模型,因此本文在前期研究的基礎上[12],選擇扁平形截面聚酯纖維作為研究對象,對經典的DB模型進行參數修正并驗證吸聲系數的預測效果,以期為異形截面聚酯纖維的吸聲性能預測模型的快速建立提供參考。
1 Dclany-Bazlcy模型

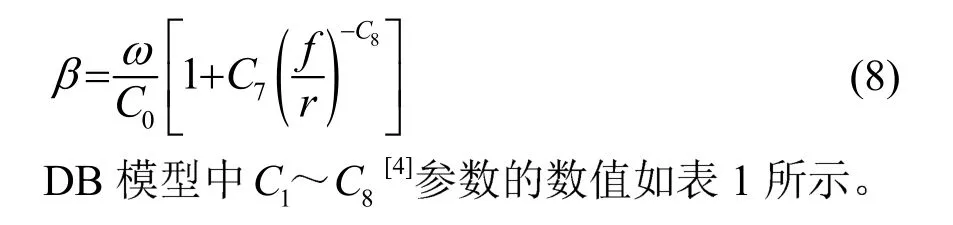
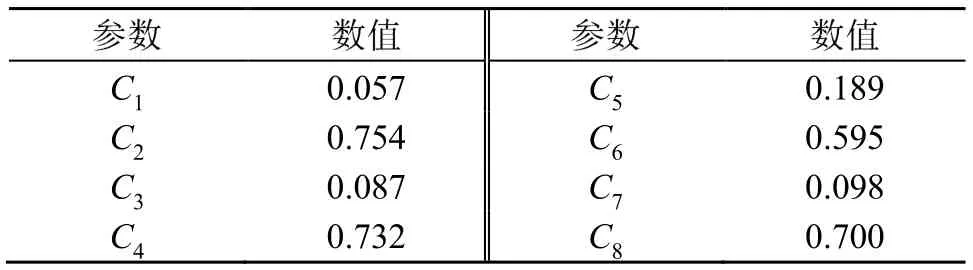
表1 DB模型C1~C8的參數數值Table 1 Values of ParametersC1~C8in DB model
從DB模型可得,纖維材料吸聲系數的預測僅需材料厚度和流阻兩個參數。由于流阻較難測量,Dclany和Bazlcy給出了相應的經驗公式[3,5]:

其中:A=25.989,B=1.404,ρ為密度(g·cm-3)。其由簡單的冪指關系通過材料的容重預測其流阻,因此不可避免地存在經驗公式帶來的預測誤差。
2 實驗材料和設備
2.1 纖維材料的制備
本研究采用開松-梳理-熱壓法[13]分別制備了圓形和扁平形兩種截面形狀的聚酯纖維板用于后續研究。纖維材料制備過程如下:將聚酯纖維和低熔點聚酯纖維開松混合,稱重鋪放于模具中,然后在平板熱壓機中通過190 ℃的溫度熱壓10 min,室溫冷卻后得到不同參數的聚酯纖維板,其相關物理參數如表2所示。制備樣品的材料及成品圖如圖1所示。
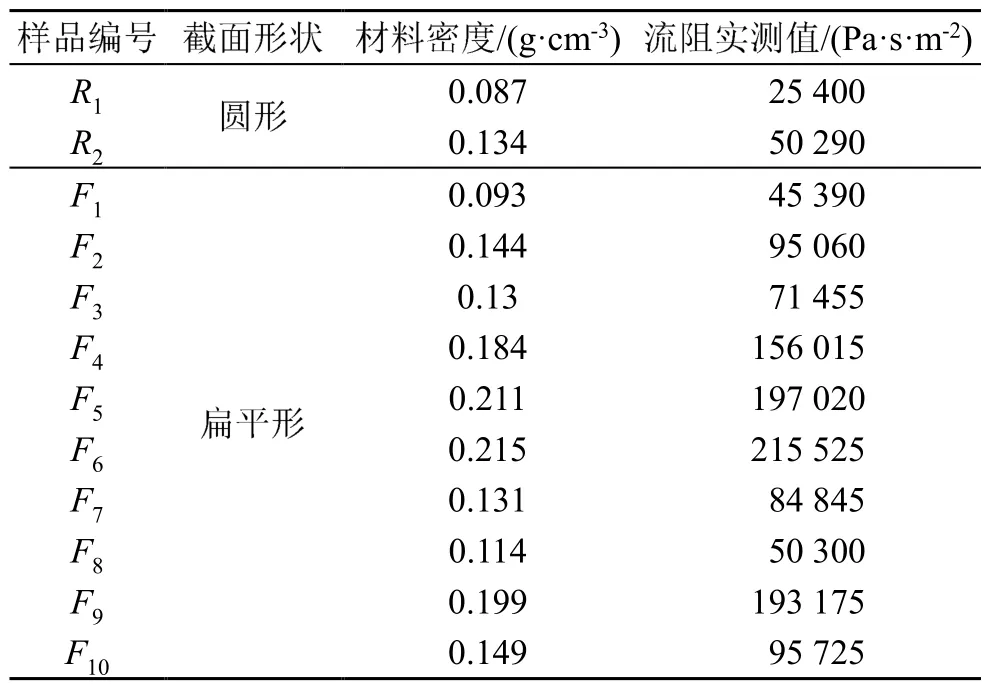
表2 纖維板物理參數(厚度為7 mm)Table 2 Physical parameters of fiberboard (thickness: 7 mm)

圖1 制備樣品的材料及成品圖Fig.1 Preparation of sample materials and finished product
2.2 儀器與設備
本文采用 YP402N電子天平(上海精密科學儀器有限公司)測量材料的質量,計算得到聚酯纖維板的容重。測試符合GB-T 26497-2011[14]標準。
本文采用四通道阻抗管BSWASW4224(北京聲望聲電技術有限公司)測量材料的吸聲系數。阻抗管采用傳遞函數法[15]測量聲波垂直入射時的吸聲系數。其測量樣品小易獲取,測量方法簡單,適合推廣普及,阻抗管如圖2(a)所示。

圖2 測試設備Fig.2 Picture of testing equipment
本文采用流阻測試與分析系統SIGMA(加拿大Mccanum 公司)測量流阻數據,在極低的壓強下測量空氣的線速度得到流阻。測試方法符合標準9053-2018[16]和 9053-2020[17],儀器如圖2(b)所示。
本文采用Olympus BX43熒光正置顯微鏡觀察不同纖維的截面形狀。測試方法符合 GB/T 2609-2015[18]標準。
2.3 研究方法
采用扁平截面纖維的物理參數對模型參數進行非線性擬合,得到修正后的參數值和優化后的DB模型。模型參數修正后,采用修正后的DB模型計算得到吸聲系數計算值,將計算值與實際測量值對比得到相對誤差。以相對誤差是否達到15%為衡量指標,若誤差率e>15%,則重新修正模型參數直到誤差率e≤15%。計算和測量值的相對誤差率計算公式為

其中:e為誤差率;α0為平均吸聲系數實測值;α1為平均吸聲系數預測值。
采用如圖3所示的流程,進行參數修正。
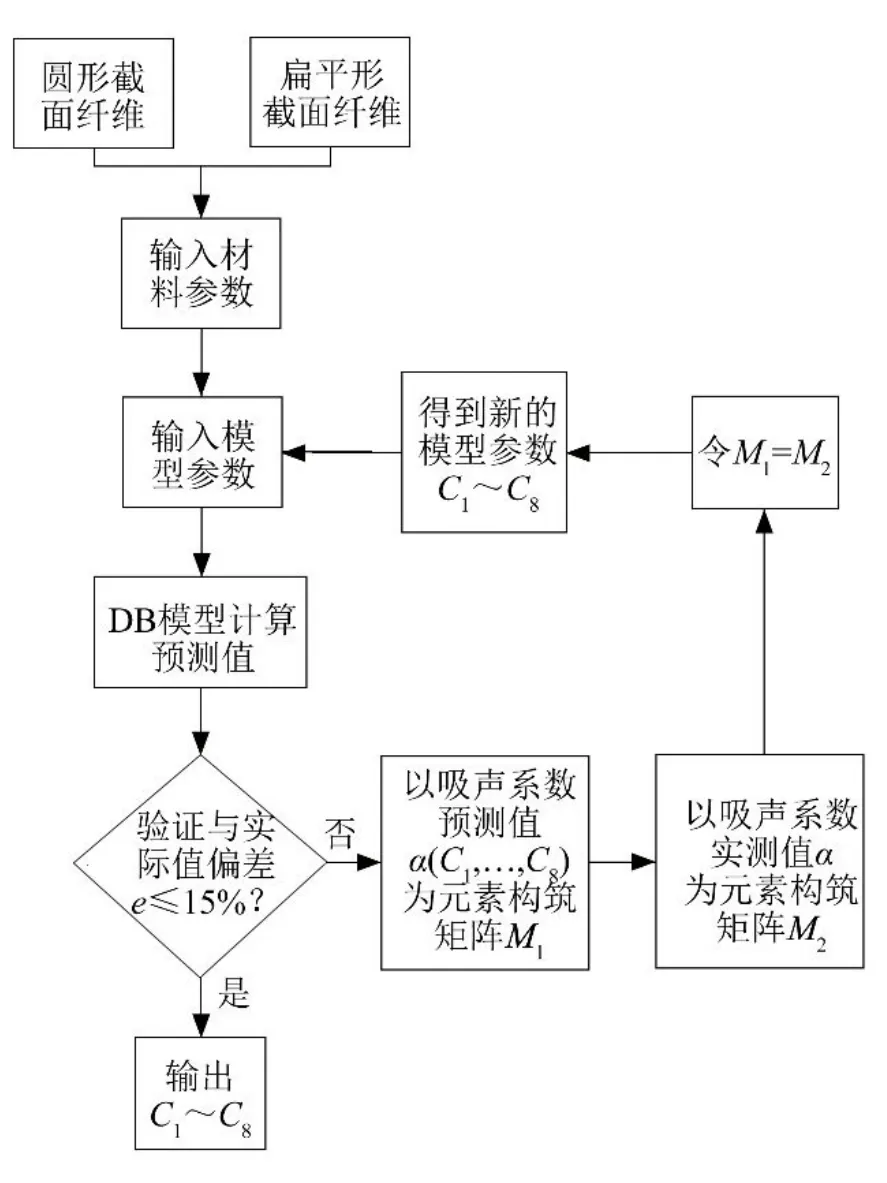
圖3 DB模型優化流程圖Fig.3 Flow chart of DB model optimization
3 結果與分析
3.1 圓形和扁平截面纖維吸聲系數的預測結果對比
為了比較DB模型計算圓形和扁平形纖維材料吸聲性能的差異,選取了表2中容重接近的圓形(R1、R2)和扁平形(F1、F2)截面聚酯纖維材料,輸入到DB模型,分別得到兩種截面形狀聚酯吸聲系數的預測值,并將吸聲系數預測值與實際測量值進行了比較,如圖4所示。
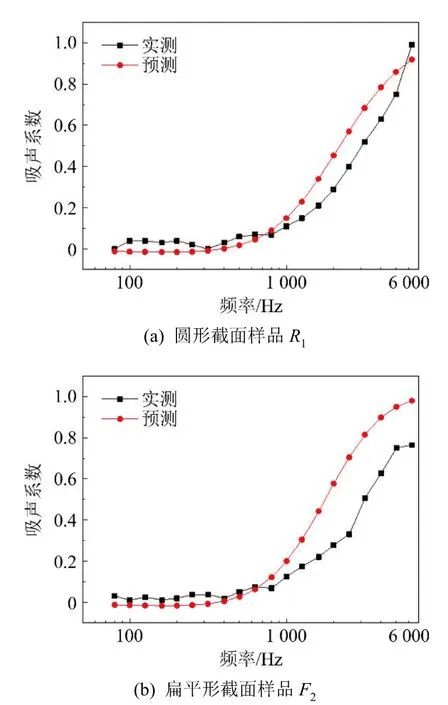
圖4 實測吸聲系數與DB模型預測吸聲系數的對比Fig.4 Comparison between measured and DB model predicted sound absorption coefficients
從圖4可以看出,圓形截面纖維采用原DB模型預測平均吸聲系數相對誤差較小,為13.00%;而扁平形纖維采用DB模型預測平均吸聲系數相對誤差較大,為36.64%。表明采用原DB模型能較為準確地預測圓形截面纖維的吸聲系數,但用于預測異形截面纖維時,會有較大誤差。因此有必要對DB模型參數進行修正,使其更適用于扁平形截面纖維。
造成兩者預測精度差異的原因可能是相同容重下,扁平形纖維由于其比表面積較大,氣-固相聲阻也較大,從而增大了聲波穿過時的粘滯阻力作用[12],使得聲波通過扁平形截面纖維時的能量損耗增加,吸聲系數由此增大。在DB模型中,這種阻力作用以流阻形式表示。根據公式(9)可得,相同容重的材料流阻應該相同。但是通過實測數據發現,相同容重下扁平形截面纖維與圓形截面纖維的流阻存在著巨大的差距,這也從側面證明了扁平形截面纖維的粘滯阻力作用更加明顯。因此,研究認為有必要根據實測流阻數據修正DB模型參數,減少原DB模型的預測誤差,而修正后的DB模型將適用于扁平形截面纖維。
3.2 參數修正研究
為此選取表2中F1-F6號六組樣品,將這些樣品的實測流阻、材料厚度代入DB模型,假設C1~C8為未知數,從而構筑矩陣M1:
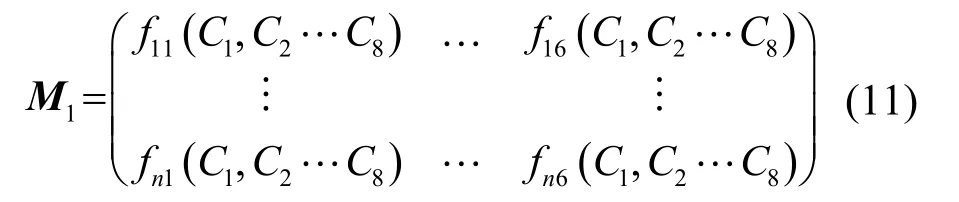
該矩陣表示通過 DB模型預測得到的吸聲系數。其中每一行表示同一頻率下6組材料的吸聲系數預測值;每一列表示同一材料在不同頻率下的吸聲系數。同時,將6組材料實際測量的吸聲系數構筑矩陣M2:

該矩陣表示6組材料實際測量的吸聲系數,其中每一行為同一頻率下6組材料的吸聲系數,每一列表示同一材料不同頻率下的吸聲系數。
M1和M2相等,通過擬合得到C1~C8數值,即修正后的DB模型參數,如表3所示。
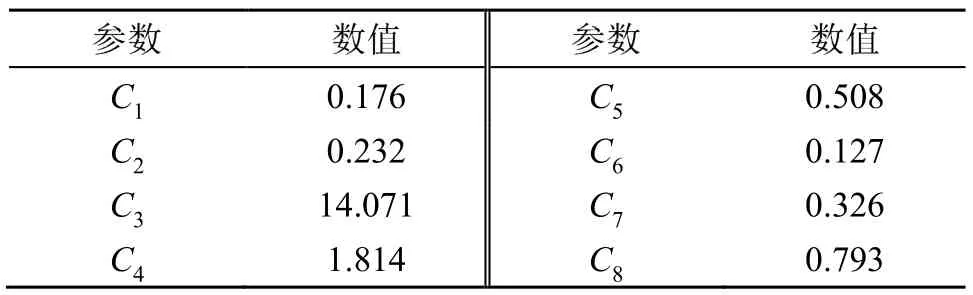
表3 擬合得到的參數C1~C8Table 3 ParametersC1~C8obtained by fitting
3.3 優化后DB吸聲模型的效果驗證
將擬合后得到的C1~C8的值代入DB模型得到優化模型,以表2中F7~F104組扁平形聚酯纖維樣品為研究對象,通過比較模型預測值與實際測量值來驗證修正模型的效果。圖5是優化后DB模型吸聲預測值與實測值的比較曲線。
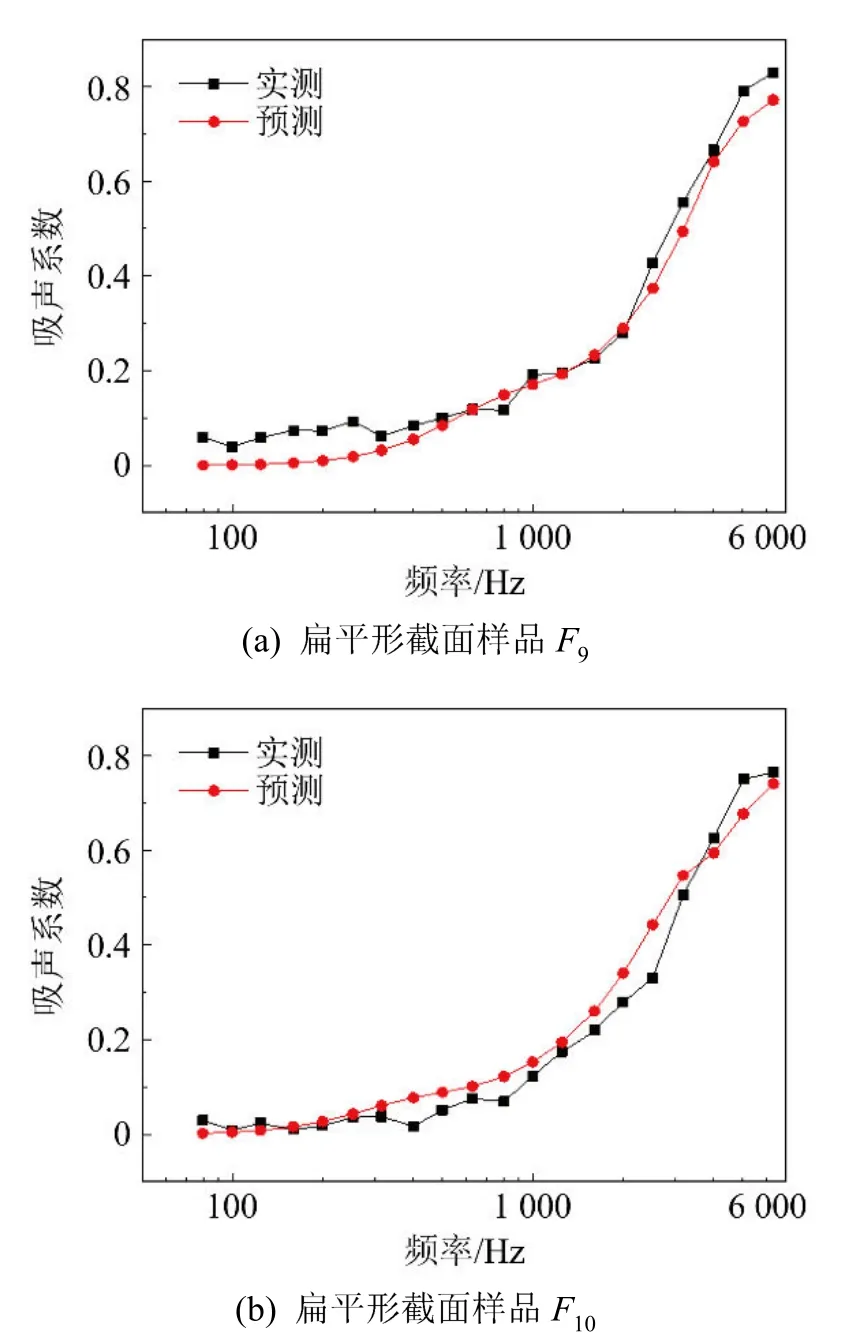
圖5 優化后DB模型預測數據與實測數據驗證結果示意圖Fig.5 Verification results of the optimized DB model predicted data and the measured data
表4列出了DB模型優化前后誤差對比。由表4可以得到,優化后的DB模型預測扁平形聚酯纖維的吸聲系數所得到的誤差遠遠低于未優化模型的誤差。平均相對誤差從起初的 36.64%下降到9.16%,降低率達到75.00%。由此可見,參數擬合后得到的優化DB模型能較準確地預測扁平形聚酯纖維材料的吸聲系數,從而為異形纖維吸聲性能的進一步準確預測提供了方法。
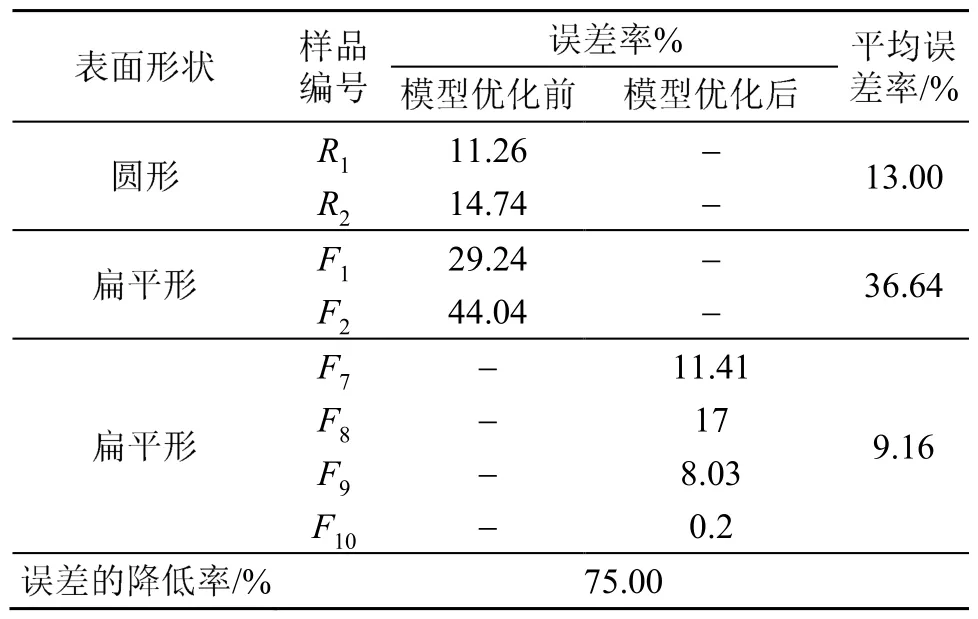
表4 DB模型優化前后誤差率對比表Table 4 Comparison table of error rates before and after DB model optimization
4 結 論
本文比較了DB模型對于圓形和扁平形截面聚酯纖維吸聲性能預測的準確性,通過實測的流阻、吸聲系數和材料厚度擬合八個無量綱常數C1~C8,從而得到了優化模型,并顯著提升了DB模型預測扁平形纖維吸聲系數的效果。
研究表明DB模型適合于常規圓形截面纖維的吸聲性能預測,誤差率僅為 13.00%。而對于異形(扁平形)截面纖維的平均誤差率達到36.64%。
采用實測流阻數據修正模型參數,得到的優化DB模型吸聲系數的預測值與實驗測量值十分接近,平均誤差率僅為9.16%,相對誤差降低率為75.00%,從而證明了參數修正對于模型優化的可行性。
受到時間及實際條件的限制,本文只選取了一種異形截面(扁平形截面)的纖維來優化 DB模型,后續將考慮對更多截面纖維的模型優化,以期構建異形截面纖維客觀參數與DB模型優化參數的聯系。

