耦合MBSs三量子點輸運性質研究

秦 芳

(河北民族師范學院 物理與電子工程學院，河北 承德 067000)

Majorana費米子是一種遵循Non-Abelian統計的任意子，極適合構建量子比特,應用于拓撲量子計算，此外Majorana費米子還可能是暗物質的一種備選粒子。因此從提出起就引起人們的廣泛關注。遺憾的是至今仍然沒有發現以單粒子形式存在的Majorana費米子。理論預言在拓撲超導體的渦核或同時存在超導性和強自旋軌道耦合的納米線末端存在著一種性質類似于Majorana費米子的準粒子—馬約拉納束縛態(MBSs)[1-2]。但大多數拓撲超導體都需在很低的溫度下實現，難以制備異質結構。近期，Zhang、Wang等人發現鐵超導體FeTe0.55Se0.45表面滿足拓撲超導電性的必要條件，在這種超導體中，通過觀察由外部磁場引起的漩渦核心處的零偏壓電導峰，可以更簡單地觀察到MBSs[3-4]。Liu等也通過隧穿譜中的零偏壓電導峰發現 (Li0.84Fe0.16)OHFeSe可作為研究MBSs的理想平臺[5]。由此可見，零偏壓電導峰的存在是產生MBSs 的有力證據。此外，人們還利用4πJosephson效應、非局域量子隧穿等方法來探測MBSs。

理論上常將MBSs與量子點體系相耦合，通過耦合前后體系輸運性質的變化來證明MBSs的存在[6-8]。文獻[6]研究了耦合MBSs 單量子點體系的輸運性質。結果表明，MBSs強烈影響通過量子點的電導。零溫時，若納米線處于拓撲相，電導峰值為e2/2 h；若納米線處于平庸相，電導峰值為e2/h；若體系耦合一普通費米子，電導峰值為0。在文獻[7]中，作者研究了兩種模型的電導，在量子點—MBSs—量子點體系中，發現零費米能處電導等于e2/h，不隨體系眾多參量的變化而改變；研究量子點—量子點—量子點—MBSs體系發現，當量子點為偶數(奇數)時，零費米能處電導等于2e2/h(e2/h)。文獻[8]將MBSs耦合到T型量子點體系的末端。研究表明，零偏壓電導峰始終等于e2/2 h，該數值不隨量子點的數目改變。

對比于單量子點和雙量子點結構，三量子點作為耦合多量子點體系的最小結構單元有多種構型，不僅可以通過參量的設置實現單、雙量子點體系的全部信息，還可以獲得單、雙量子點體系無法實現且有實際應用價值的輸運性質，因此更具研究價值。本文將三個量子點排成一列，一對MBSs耦合在量子點1、2間，將這兩個量子點各自與正常金屬電極相連，利用非平衡格林函數的方法重點研究體系參量變化時MBSs對反射系數的影響。

1 模型

如圖1所示，具有強自旋軌道耦合的半導體納米線的兩端分別與量子點1、2相連，并將該納米線置于s-波超導體上，且沿納米線的方向施加一均勻外磁場，則在適當的條件下兩個局域的MBSs將會出現在在納米線的兩端[9]。兩正常金屬電極分別連接到量子點1、2 的兩側，量子點3與量子點2耦合。體系哈密頓：

H=Hdots+HLeads+HT+HM

(1)

其中：

(2)

(3)

利用非平衡格林函數技術、Fourier變換及Keldysh公式可得從左電極流入的電流：

(4)

(5)

由于零溫下系統的電導[10]

(6)

所以在接下來的討論中只畫出了反射系數隨費米能的變化曲線。

2 結果與討論

僅考慮ε1=ε2=ε3=ε0，εM的情況。

固定量子點1與MBS的耦合強度λ1，量子點2與MBS的耦合強度λ2取不同的值時反射系數隨費米能的變化如圖2(b)～(d)所示。圖(a)為未耦合MBSs時反射系數曲線，圖中出現三個峰值等于1的反射峰，分別位于E=0、E=±t處。這是由于此時量子點未與MBSs連接，因此沒有拓撲超導體與之量子點相連，所以體系沒有Andreev反射發生，TA=TH=0，圖中出現的反射曲線僅由單電子遂穿產生。圖(b)～(d)分別為λ2<λ1、λ2=λ1及λ2>λ1時的反射曲線，其中紫色和紅色曲線分別為局域Andreev反射和交叉Andreev反射，藍色曲線為單電子遂穿，黑色為系統總反射。當λ2<λ1時，Andreev反射出現5個反射峰，分別位于E=0、E≈±λ1和E≈±λ2處。由于同電極的Andreev反射TA貢獻了兩次，所以在對電導的貢獻中這一項前乘以了系數2，恰好是交叉Andreev反射的2倍。當λ2=λ1時，Andreev反射僅余E=0一個峰。而當λ2>λ1時，其余兩對峰再次出現。三種情況下零點Andreev反射峰的形狀和大小始終沒有發生變化，一直固定在0.25。TE曲線恰好與Andreev反射曲線的峰谷相反，即由于量子點與MBSs相耦合，單電子遂穿在Andreev反射峰位置發生了反共振，并且E=0處單電子遂穿系數恰好等于Andreev反射系數。這是由于量子點1、2分別與一個MBS(即“半個費米子”)相連，所以反共振并未使透射系數變為零，而是降為1/4。值得注意的是當量子點與MBSs耦合后，零點反射值始終等于1，不隨λ2的改變而發生變化，體現了MBSs不受局域擾動的特性。為了進一步研究MBSs的這一特性，我們分別改變體系其它參量觀察反射曲線的變化。

圖3為反射系數隨體系與電極間的耦合強度λ2的變化曲線。由圖可見，T—E曲線呈現四個反射峰，主要由單電子遂穿導致，峰值位置不變，各峰寬度隨著λ2的增加變寬。零點Andreev反射峰的變化與之相反，隨著λ2的增大，一個尖銳的峰將該位置原有的平臺取而代之。零費米能處反射系數仍然一直固定在1。

量子點2與量子點3間的耦合能t對反射系數的影響如圖4所示。由圖(a)可見，t對反射曲線的影響主要集中在零費米能附近，E=0兩側的峰值隨著t的增大變寬。由圖(b)、(c)可見，t對Andreev反射峰的影響明顯，隨著t的增大零點反射峰顯著變寬，在其兩側一對新的對稱反射峰逐漸出現，原本位于零費米能兩側的反射峰峰值變大，并分別向遠離零點的兩側對稱移動。單電子遂穿曲線的變化與Andreev反射曲線恰好相反，各峰值隨著t的增大減小，峰值位置向偏離零費米能的左右兩端稍有偏移。由此可見，隨著量子點2與量子點3間的耦合能的增大，Andreev反射作用逐漸增強，由于單電子遂穿減弱，總反射曲線的各峰值幾乎沒有變化。零費米能處的各反射系數均沒變化。

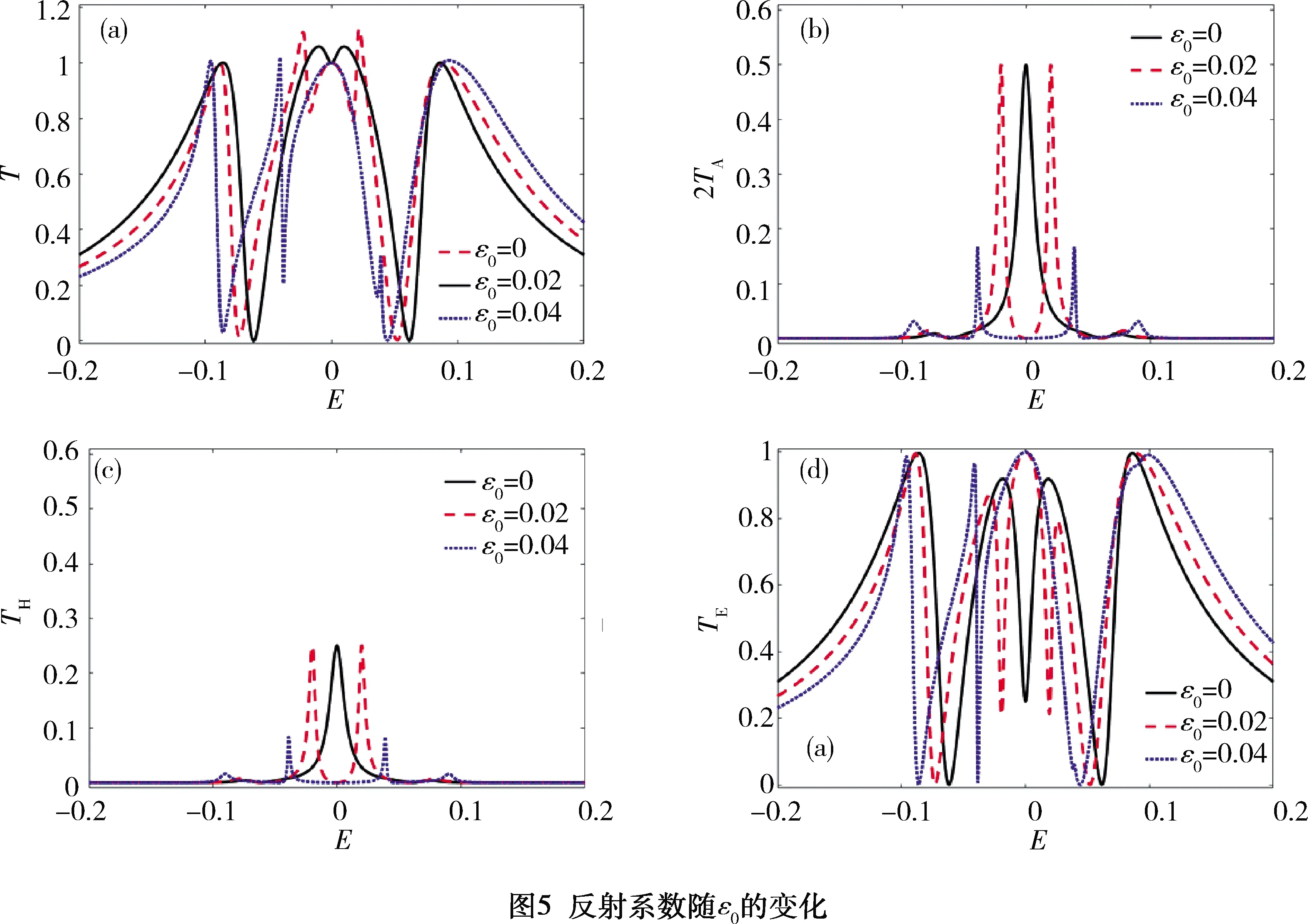
圖5為改變量子點能量時反射曲線的變化。該組曲線明顯不同于前面三組。首先，隨著λ2的增加，反射曲線呈現出不對稱的特點，觀察圖5(b)～(d)發現這一情況由單電子遂穿導致。在單電子遂穿曲線中零費米能的左側出現了兩個明顯的Fano共振。其次，隨著λ2的增加，零費米能處的Andreev反射值減小，而單電子遂穿反射值增加，由于二者變化的幅度相同，所以該點的總反射值依舊始終等于1。充分體現了MBSs的魯棒性。

3 結論

本文利用非平衡格林函數方法研究了耦合MBSs的正常金屬/三量子點/正常金屬模型的反射系數隨費米能的變化規律。結果表明，當體系耦合MBSs后，改變體系λ2、Γ和t，曲線呈對稱分布，并且無論這些參量如何變化，總反射系數始終固定在1，Andreev反射系數始終等于0.5，是交叉Andreev反射系數的2倍，充分體現了MBSs的魯棒性。當改變參量ε0時，由于單電子遂穿曲線中出現了兩個明顯的Fano共振峰，反射曲線呈現出不對稱的特點。因此耦合MBSs后三量子點體系反射曲線新的特征可作為判別MBSs存在的重要依據。