基于EMD方法的X波段雙偏振雷達衰減訂正

李 海， 馮興寰, 孟凡旺

(1. 中國民航大學天津市智能信號與圖像處理重點實驗室， 天津 300300；2. 中國航空工業集團公司雷華電子技術研究所， 江蘇無錫 210403)

0 引言

天氣雷達是監測和預警突發災害性天氣最有效的手段，常規的天氣雷達通過反射率與降雨率的經驗關系實現對降雨的探測和預報，然而此類雷達無法滿足對大范圍降水測量準確度的要求，雙偏振雷達能提高天氣雷達的探測能力，包括降水估算能力和粒子相態識別能力。與C波段和S波段相比，X波段雙偏振雷達對目標的定位更準確，并且具有天線尺寸小、易于移動等優點。當雙偏振雷達探測氣象環境時，回波信號會被路徑中降雨區域吸收，使接收端的反射率產生衰減，特別是X波段(中心波長3 cm)，由于其波長較短，反射率衰減問題更為嚴重，使實測的反射率與真實的反射率之間存在差異，導致雙偏振雷達對降雨估計不準確，因此必須進行衰減訂正。

Zhang等根據雷達氣象方程和-關系，提出了雷達徑向逐庫算法進行衰減訂正，該算法減小了過度訂正問題，但沒有解決衰減訂正中不穩定的-關系。隨著雙偏振雷達的發展，Rahimi提出差分傳播相移與衰減率之間可以近似為線性關系，在使用差分傳播相移進行衰減訂正時需消除后向散射以及環境噪聲的影響，得到準確的差分傳播相移。常見的平滑濾波，中值濾波等方法雖然能夠改善差分傳播相移數據的平滑性，但失去了對原有數據變化趨勢的反映。Hubbert等提出采用FIR和IIR低通濾波器估計差分傳播相移，該方法可得到差分傳播相移的平均走勢，但隨著距離庫的增加，不能有效抑制差分傳播相移波動。何宇翔等提出的卡爾曼濾波方法能夠對差分傳播相移進行較精確的估計，但這類方法對于距離門之間數據的關聯性較強，導致運算速度較慢。杜牧云等提出了小波分析法，通過小波分析估計得到的差分傳播相移具有良好的平滑度，并減少了差分傳播相移率的負值，但是此方法需要選擇合適的小波基，影響運行速度。Bringi等提出了迭代濾波方法，該方法能夠達到剔除干擾的目的，但是迭代次數難以確定，數據處理時間較長。文獻[11]利用MCMC方法對差分傳播相移進行處理，該方法能對差分傳播相移進行濾波處理，但MCMC方法存在一個顯著問題就是需要計算接受率，導致計算量大，并且由于接受率的原因導致算法收斂時間變長。目前，上述方法均是將降水區域視為連續的區域進行衰減訂正處理，且將天氣雷達不同偏振參量的關系理想化為線性關系，當雷達測量值出現不連續或缺測點時將影響整個降雨區域的衰減訂正效果，因而這些方法具有一定的局限性。

本文提出了一種基于EMD方法的X波段雙偏振雷達衰減訂正，該方法首先利用EMD方法對總差分傳播相移進行自適應分解，獲得由高頻到低頻分布的多個IMF，其次通過皮爾遜相關系數準則對IMF進行篩選，將有用的IMF進行重構獲得差分傳播相移，且將差分傳播相移采用最小二乘法擬合差分傳播相移率，然后將求得的差分傳播相移與差分傳播相移率采用自適應約束方法進行反射率衰減訂正，最后對所提方法進行了仿真實驗。實驗結果表明所提方法可以降低觀測數據帶來的誤差，并極大程度上保證差分傳播相移的遞增性，從而實現更加準確的衰減訂正。

1 基于EMD的衰減訂正方法

本文使用EMD方法進行衰減訂正，首先采用EMD方法估計差分傳播相移，之后再對差分傳播相移采用最小二乘法估計差分傳播相移率，最后對求得的差分傳播相移與差分傳播相移率采用自適應約束方法進行反射率衰減訂正。下面將分別進行詳細描述。

1.1 基于EMD的差分傳播相移估計

假設降水區域包含個距離庫，將第個距離庫的水平和垂直偏振波相位分別記為()、()，則該距離庫的差分傳播相移()為

()=()-()

(1)

它表示水平、垂直偏振波傳播到第個距離庫之后散射回來的信號相位差。實際雷達觀測到的總差分傳播相移()由差分傳播相移與后向散射差分相移構成，表示為

()=()+()

(2)

式中，()表示該距離庫后向散射差分相移，是散射過程中降雨粒子本身引起的相位差。從頻率上看，()屬于高頻噪聲。對于不同強度的降雨區，()會隨著雨滴直徑的增大而增大，導致()在距離廓線上表現出短距離內的波動。由式(2)可以看出，當()近似為常數或能被忽略時，可以將()作為()的估計值，否則就需要濾除()，估計準確的()。

1.1.1 EMD分解

EMD算法是一種自適應的信號去噪方法，該算法可將總差分傳播相移自適應分解為多個IMF和殘余項之和，且每個IMF都應滿足以下2個條件：1)在整個曲線中，極值點和過零點的數目相等或至多相差1個；2)在任意局部區間，曲線的局部極大值包絡線和局部極小值包絡線的平均值為0。EMD分解包括提取分量、篩選IMF、計算余項三個部分：

(a) 提取分量

確定原始序列={(1),(2),…,(),…,()}的局部極值序列，記為={()|?}，其中，表示所有極值點的集合。局部極值序列分為局部極大值序列與局部極小值序列(例如，局部極大值定義為序列中的某個距離門所對的總差分傳播相移值，其前一距離門的值比它小，后一距離門的值也比它小)。

從序列中提取相鄰極值點()、()之間的局部序列設為={(),…,(),…,()}，其中，≤≤。根據文獻[14]，求的局部均值()為

(3)

=-

(4)

(b) 篩選IMF

若符合IMF條件，就是的第一個IMF；若不滿足IMF的條件，繼續將作為新的信號，重復步驟(a)進行分解。在實際中，通常無法滿足IMF條件，假設經過(一般小于10)次分解后，有以下式(5)成立，則認為其滿足IMF條件：

(5)

式中，為門限，一般取值為02～03。

那么原始信號的第一個IMF可記為

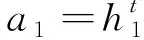
(6)

(c) 計算余項

將得到的從中分離出來，得到余項=-，將作為新的信號，重復步驟(a)～(b)繼續進行分解，依次可得到第2，第3，…，第個，…，第個IMF，記為

(7)

當余項變成一個單調信號時，EMD分解過程停止。

通過上述分解過程，可將分解為個IMF與余項的和，記為

(8)

基于EMD的總差分傳播相移分解流程如圖1所示。

圖1 總差分傳播相移分解流程圖

1.1.2 EMD重構

傳統的EMD憑借經驗選取前幾個IMF重構差分傳播相移，這會導致重構的差分傳播相移中混入多余的后向散射或漏掉某些有用信息，為了克服這一問題，本文提出利用皮爾遜相關系數準則(||)分析原始信號與EMD分解得到的個IMF相關性，確定最佳IMF數目。

首先計算=((1),(2),…,(),…,())與=((1),(2),…,(),…,())的值，定義式為

=1,2,…,

(9)

表1 皮爾遜相關系數評估標準

通過計算EMD分解得到的個IMF與原始信號的||值，找到合適的分界點∈(0,1)，確保除去噪聲較大的前(∈(1,2,…,))個，其他IMF的||值穩定在評估標準范圍內。

經過EMD分解后，總差分傳播相移可以表示為

(10)

式中，～表示噪聲分量，+1～表示信號分量，表示余項。差分傳播相移由信號IMF與余項共同構成，即

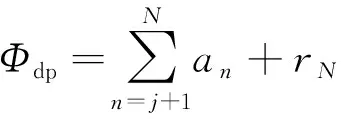
(11)

基于EMD的差分傳播相移重構流程如圖2所示。

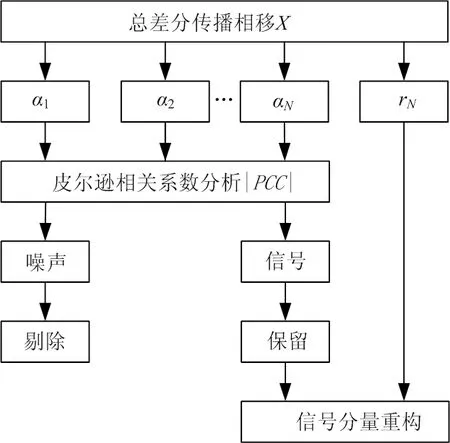
圖2 差分傳播相移重構示意圖

1.2 基于最小二乘法的差分傳播相移率估計

在降水區距離內含有個距離庫，第個距離庫對應值為()，用最小二乘法擬合這個庫對應的，根據擬合曲線的斜率即可得到雨區距離的值,表示為

(12)

1.3 基于自適應約束方法的反射率衰減訂正

衰減率對接收的反射率影響較大，且隨著探測距離的增加而增加，造成反射率估計誤差，因此本文在自適應約束算法的基礎上，根據EMD方法處理得到的與最小二乘法擬合的，提出了適用于雙偏振雷達的自適應約束方法進行反射率衰減訂正。該方法首先對雨區徑向數據劃分區間，根據-的關系，計算所有區間的衰減系數，完成整個徑向數據的衰減訂正。

由文獻[18]可知，雷達反射率衰減訂正原理如式(13)所示：

(13)

式中，()與()分別為訂正前后的第個距離庫反射率，()為第距離庫的衰減率。

(14)

(15)

(16)

最后將最優()代入式(13)中得到訂正后的()。

對反射率處理的具體流程如圖3所示。

圖3 衰減訂正處理流程圖

2 實驗結果及分析2.1 差分傳播相移估計效果分析

本文使用的是ARM(Atmospheric Radiation Measurement Climate Research Facility)探測到的X波段天氣雷達數據。該雷達采用雙偏振體制，同時在水平和垂直偏振中傳輸，其主要包括偏振參數，，等。下面通過仿真試驗分析了不同濾波方法的估計效果。

圖4為X-SAPR雷達于0.5°俯仰角、30°方位角的雷達觀測數據，以及經過不同濾波方法的徑向距離廓線圖。從圖中可以看出，原始信號(圖4(a))由于外界噪聲存在較大的波動，但基本保持遞增趨勢。由均值濾波(圖4(b))與FIR濾波(圖4(c))后的處理效果可以看出，這兩種方法對的波動起伏有較好的平滑效果，但隨著平滑庫數增大，不能有效抑制波動。卡爾曼濾波(圖4(d))由于缺乏先驗數據，造成初始數據失真。采用EMD方法對原始信號進行分解得到7個IMF，從低到高依次計算各IMF與原信號的||值分別為0.07，0.13，0.15，0.20，0.23，0.36，0.58，可知前3個IMF的||值均在0.00～0.19極弱相關這一范圍內，為噪聲分量，后4個IMF的||值均大于0.19，為信號分量，對后4個IMF進行有效重構，其結果如圖4(e)所示，可以看出，數據的毛刺和波動均得到很好抑制，數據的連續性和平滑度有了顯著提升，即去除了后向散射的影響，這也有利于對數據進行后續處理及應用。綜上可見，EMD方法較之常規方法具有更明顯的處理效果。

(a) 原始數據

圖5為X-SAPR雷達于0.5°俯仰角觀測數據的PPI圖及經過EMD方法后的PPI圖。從圖中可見，在原始數據PPI圖(圖5(a))中，大部分徑向都具有較為明顯的層次性，顏色上表現為分層漸進遞增形式，但也存在許多“麻點”(黑框所選區域為麻點)，即為波動數據點；經過EMD方法后(圖5(b))，數據整體層次性得到明顯加強，顏色分布均勻，且原始數據的有效的氣象回波也得到了很好的保留。

(a) Ψdp原始數據

為了進一步分析不同濾波方法對差分傳播相移估計的影響，分別通過平均波動指數、相對誤差、互相關系數進行降雨估計性能分析，計算公式為

(17)

(18)

(19)

式中，()表示實測值，()表示經過處理后的值，通過來比較距離廓線的波動情況，的值越大，說明徑向距離廓線的波動性越大；通過來比較數據可靠性，值越小數據的可信度越高；通過來比較數據變化趨勢的一致程度，值越大表明線性一致程度越高。

表2統計了()經本文提出的方法與常規方法處理并應用于降水估計()的、和。根據統計結果可以看出，()經常規方法處理后的和較大，而EMD方法處理的()的與較小，且值相對較大，說明EMD方法對()數據的處理波動較小，可靠性高，應用于降水估測的精度最高。

表2 不同濾波方法對QPE影響的對比圖

2.2 差分傳播相移率估計效果分析

圖6為X-SAPR雷達于0.5°俯仰角、30°方位角的雷達觀測數據，以及經過不同濾波方法的徑向距離廓線圖。結果表明，經過均值濾波、FIR濾波、卡爾曼濾波和EMD方法處理后估計的的負值數量分別為182，185，167和148。說明EMD方法能夠有效地減少的負值，保證數據的基本趨勢。

(a) 原始數據

2.3 反射率衰減訂正效果分析

X波段雙偏振雷達探測的徑向距離為40 km，一個距離庫表示100 m。圖7為同一徑向的反射率衰減訂正結果對比圖，從圖中可以看到，變化與的變化趨勢是相對應的。在初始距離庫，雨區的衰減較少，反射率基本在20dBz左右，而在第200個距離庫處有一強回波區域，雨區的衰減較多，使用EMD方法進行訂正后的反射率因子能夠在保持原始數據變化趨勢的同時，對其進行有效的衰減訂正。

圖7 反射率衰減訂正對比圖

圖8為反射率因子訂正前后PPI對比圖。由圖8(a)可知，強回波的區域分布離散，主要集中在圖中心位置，雷達強回波反射率因子一般在30～40 dBz，由圖8(b)可知，經過衰減訂正后，雷達回波反射率因子的訂正值一般在1～5 dBz。強回波區域擴大，回波中心更為明顯，訂正值達到了5～10 dBz。

由于S波段雷達基本上不存在雨區衰減，除非在一些濕雹區。因此將同時間同一區域內的反射率因子訂正后的效果與S波段數據進行對比，其效果與S波段探測結果越相似，則認為訂正效果越好。S波段雙偏振雷達的探測距離范圍為230 km，而X波段的探測距離范圍為40 km，所以X波段氣象雷達包含在S波段雙偏振雷達的探測范圍內，圖8(c)為S波段雙偏振雷達回波反射率因子，黑色方框中的區域作為X波段雙偏振雷達衰減訂正后的效果參照圖。對比圖8(a)、圖8(c)可以看到，X波段雙偏振雷達衰減更為嚴重。對比圖8(b)、圖8(c)可以看到，經過EMD方法處理后，X波段雙偏振雷達的反射率因子中心處強回波有所加強，與S波段雷達回波反射率因子差異顯著減小，表明EMD方法對X波段雙偏振雷達衰減訂正具有一定的效果。

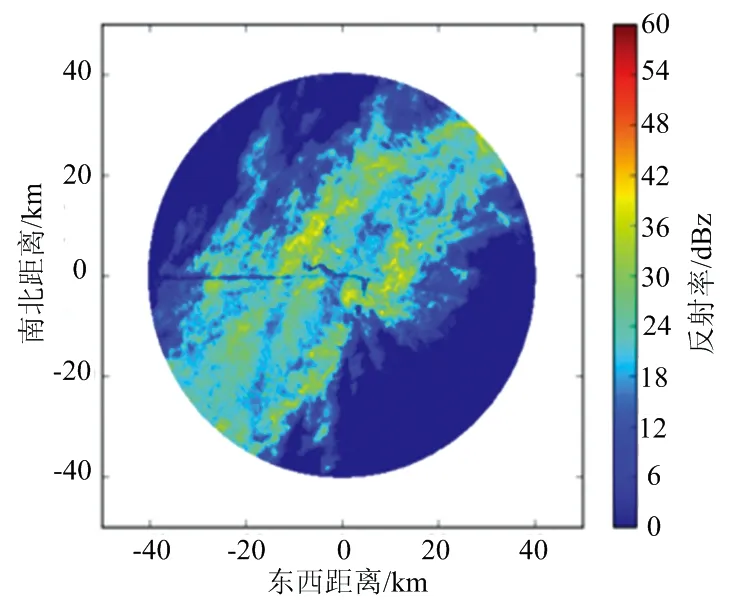
(a) X波段ZH原始數據

3 結束語

本文提出了基于EMD方法的X波段雙偏振雷達衰減訂正，首先使用經驗模式分解方法將總差分傳播相移按照頻率分布自適應地分解為多個IMF，使得原始序列平穩化，從而提高差分傳播相移的預測精度，接著利用最小二乘法估計差分傳播相移率，最后根據得到的差分傳播相移與差分傳播相移率采用自適應約束算法對反射率因子進行衰減訂正。實驗結果表明，利用EMD方法能夠實現對差分傳播相移濾波處理，并且保留原始信號的基本趨勢；利用自適應約束的方法能夠對反射率進行有效的衰減訂正，這對雷達降水量估計以及降水分類等有重要的現實意義，所以本方法具有一定的實際應用價值。