基于智能電表的住宅短期電力負載預測

楊繼革， 嚴 俊， 陳麗春， 賀樂華， 余圣彬

(國網浙江省電力有限公司 a. 衢州供電公司， b. 龍游縣供電有限公司， c. 江山市供電有限公司， 浙江 衢州 324400)

居民用電的短期負荷預測在電力系統運行中具有重要意義，準確的負荷預測有利于電力市場各方進行交易獲利，也便于市場資產的所有者安排生產運營[1-3].經典的負荷預測方法主要通過時間序列建模或模式識別技術完成[4-5].其他算法還包括但不局限于將人工神經網絡和模糊專家系統相結合，形成短期負荷預測混合模型[6].算法首先通過人工神經網絡提供臨時預測，然后由模糊專家系統進行修正[7-8].

近些年，相關研究對傳統算法進行了改進，一方面側重于對多種預測方法的融合，例如Jelena[9]結合3種不同模糊神經網絡模型來評估其負荷預測性能；Wang等[10]結合遺傳算法和神經網絡的短期負荷進行預測，通過遺傳算法優化神經網絡的參數學習性能，縮短網絡的整體訓練時間，克服了神經網絡算法容易陷入局部最優解的弊端.另一方面，學者依靠先進的計量基礎設施，例如通過智能電表進行雙向通信和實時電力分析[11-12]，從用戶的智能儀表端獲取實時測量數據，從而提供更準確的負載預測.然而，大量數據的獲取、傳輸及計算也增加了負荷預測的成本，因此，必須選擇適當的測量采樣率，以便在合適的數據量下得到所需的預測精度.

本文研究了智能電表的短期負荷預測，使用成型濾波和卡爾曼濾波相結合的算法對居民用電負荷進行預測，并分析測量采樣率對預測誤差的影響.

1 預測方法

將住宅負荷分為兩個獨立分量：天氣相關分量和生活方式分量.計算方式借鑒了將電力負荷分解為氣象敏感和非氣象敏感兩部分的處理想法[13].生活方式分量部分是負荷的決定性部分，主要取決于居民日常生活的能量消耗.天氣相關分量是高斯噪聲信號，主要影響空調、新風等負荷.從測量的歷史消耗數據中減去住宅負荷的確定性部分，留下一個零均值隨機信號，依據后續提及的頻譜確定成型濾波器.

1.1 譜分析

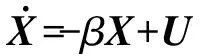
(1)

Y=αX+V(t)

(2)

式中：α和β為常數；U為單位白噪聲輸入；X為狀態向量；Y為測量值；V為單位高斯白噪聲測量值.

1.2 卡爾曼濾波

隨機系統的動態行為由簡化狀態向量和輸出向量描述，即

X(t+1)=ΦX(t)+V1(t)

(3)

Y(t)=AX(t)+V2(t)

(4)

式中，Φ、A為狀態轉換關系矩陣.噪聲變量V1(t)與V2(t)是獨立的零均值高斯噪聲及其協方差矩陣，進一步可得

(5)

式中：δ(k，l)為克羅內克符號；Q為過程噪聲協方差矩陣；R為測量噪聲協方差矩陣.

K(t)=P(t)CT[CP(t)CT+R]-1

(6)

更新后估計的誤差協方差矩陣為

[I-K(t)C]P(t)[I-K(t)C]T+

K(t)RKT(t)

(7)

使用狀態方程預測下一個狀態，即

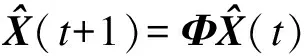
(8)

預測狀態的誤差協方差矩陣為

P(t+1)=ΦP(t)ΦT+Q(t)

(9)

重復校正和預測以產生一系列狀態估計，這種漸進分析預測的方法實際上屬于一種依據不同階段進行預測分析的技巧.已有學者提出基于混合模糊神經網絡的負荷預測器，方法分為3個階段：1)利用增長趨勢和必要的補償，將歷史負荷更新為當前負荷需求；2)使用Kohonen自組織映射來映射負載配置文件；3)神經網絡與模糊并行處理器利用輸入變量(如日類型、天氣和假日接近度)來預測當前日的負荷.該更新調整的方式與卡爾曼濾波較為相似，本文算法通過卡爾曼濾波更新預測居民用電數據.

2 結果與討論

本文通過某電網公司提供的居民負荷數據來評價方法的短期負荷預測性能，采集了某電網公司所屬供電公司2019年春季500戶居民的用電數據.圖1實線顯示了2019年4月15日一個住宅客戶的15 min間隔負載分布圖.負載數據被認為是確定性部分與隨機部分之和，用一個10階多項式擬合負荷曲線.采樣點的時間間隔為15 min，采樣點數為96，其擬合曲線如圖1虛線所示.

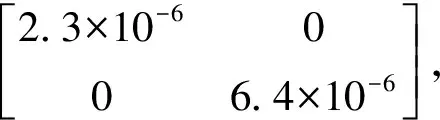
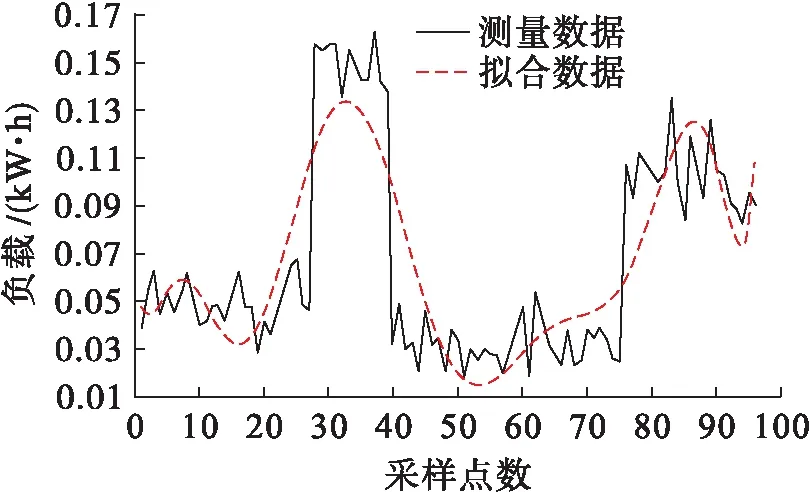
圖1 實測負荷數據與擬合數據Fig.1 Measured load data and fitting data

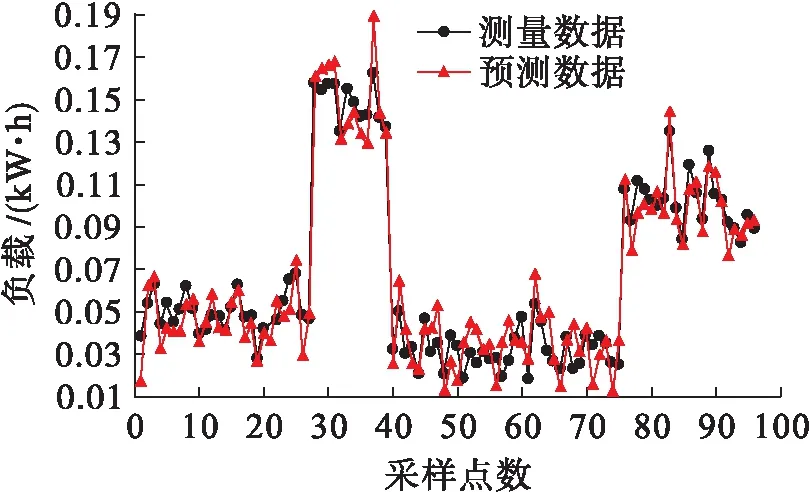
圖2 15 min間隔下測量負載與預測負載對比Fig.2 Comparison between measured and predicted loads at intervals of 15 min

智能電表的通信能力使實時測量數據的獲取成為可能，為評價所提出的預測方法在不同采樣周期和預測水平下的性能提供了機會.除了15 min的采樣周期外，還需考慮更大的30 min和1 h采樣周期.圖3、4分別展示了30 min和1 h采樣周期的住宅測量負載與預測負載對比情況.

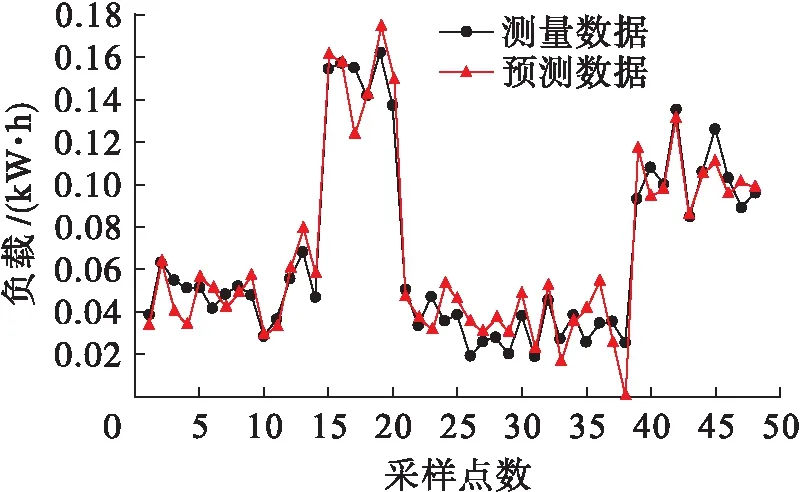
圖3 30 min間隔下測量負載與預測負載對比Fig.3 Comparison between measured and predicted loads at intervals of 30 min

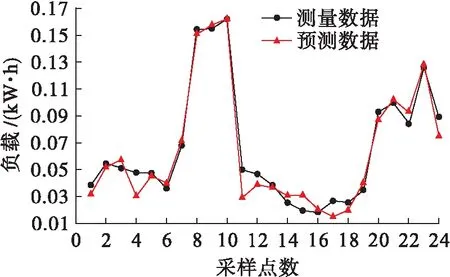
圖4 60 min間隔下測量負載與預測負載對比Fig.4 Comparison between measured and predicted loads at intervals of 60 min

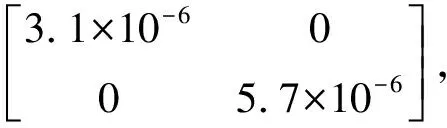
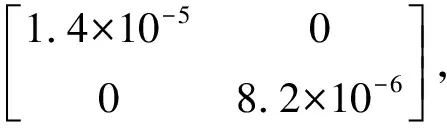
本文利用計算平均絕對百分比誤差(MAPE)來評價預測精度，表1顯示了不同采樣周期和預測時段內的MAPE情況.

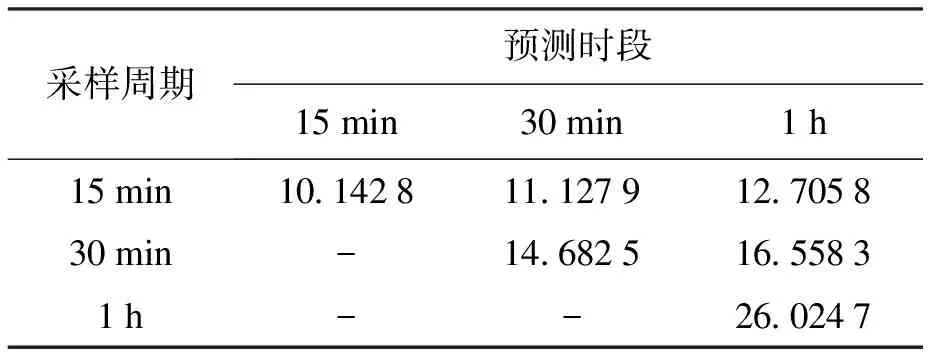
表1 不同采樣周期和預測時段下的MAPETab.1 MAPE at different sampling periods and prediction levels %

預測結果表明，在采樣周期和預測時段均為1 h的情況下，負荷預測不準確，MAPE為26.024 7%.縮短從客戶智能電表接收實時測量數據的時間間隔，可以提高方法的準確性，降低MAPE.在30 min、15 min的采樣周期內，MAPE分別降低到16.558 3%和12.705 8%.然而，采樣周期較短(15 min、30 min)會增加預測的計算負荷，因此，采樣率的選擇必須在精度與計算量之間進行權衡.

采樣率對500戶配電饋線預測精度和計算負荷的影響如圖5所示.計算負荷是按順序處理500個測量數據所需的總時間.由圖5可以看出，當采樣間隔為32 min時，計算效能和精度能夠達到最優解.

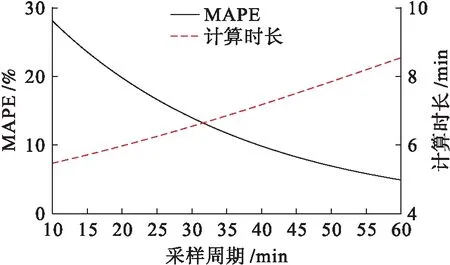
圖5 采樣率對預測精度和計算負荷的影響Fig.5 Influence of sampling rate on prediction accuracy and calculation loads

3 結 論

隨著智能電表的普及，住宅用戶的短期負荷預測可以逐步實現.利用電網公司提供的數據，本文將一個住宅負荷表示為確定性分量和隨機高斯擾動的總和，然后，利用卡爾曼濾波器對不同采樣周期的住宅負荷進行預測，評估了不同采樣周期下負荷預測的準確性.實驗結果表明，雖然更快的采樣率可以提供更多的實時測量數據，并能大幅度提高負荷預測的準確性，但額外的計算成本可能較高.因此，在限制用于預測的數據量同時，也需要達到預測精度，選擇恰當的采樣率或周期.