限位式準零剛度隔離系統的沖擊響應分析
金映麗, 張橫霖, 閆 明, 孫自強
(沈陽工業大學 機械工程學院, 沈陽 110870)
低頻隔振一直是學者們所關注的熱點話題,準零剛度隔振便是其中一種非常具有代表性的低頻隔振技術.通過正、負剛度機構并聯而成的準零剛度隔振器,在不犧牲承載能力的同時,又能獲得較低的隔振頻率,從而實現低頻甚至超低頻隔振.由Ibrahim[1]和陸澤琦等[2]發表的相關綜述可以看出,隨著國內外學者對低頻非線性隔振系統展開的深入研究,準零剛度系統在隔振方面的研究已取得一定進展.
近年來,由于對惡劣壞境下敏感設備的隔離要求不斷提高,學者們對非線性系統在沖擊隔離方面的研究逐漸增多[3-6].Ledezma-Ramirez等[7]利用非線性剛度特別是低動態剛度實現沖擊隔離,表明非線性剛度能減小位移和加速度響應;Liu等[8]研究了準零剛度隔振器在不同基底沖擊激勵下的隔沖性能,研究表明,準零剛度系統在加速度響應方面具有良好的隔沖效果;Tang等[9]分析了三彈簧準零剛度隔振器在基底激勵下的沖擊隔離特性,結果表明,準零剛度隔振系統在小振幅激勵下的加速度響應與位移響應優于線性隔振器.
由上述文獻可知,準零剛度隔振器在受到沖擊載荷作用時的加速度響應幅值較小,但相對位移響應幅值較大.設備相對基底的位移幅值過大時,很可能會超過設備與外界連接部件的允許值,甚至會超出隔振元件本身的極限變形范圍,因此,在隔振裝置的設計過程中如何限制設備的相對位移幅值顯得非常重要[10].目前,通過增加限位裝置來限制設備的相對位移是簡單且有效的方法之一[11-13].
本文為提高準零剛度系統的隔沖性能,提出限位式準零剛度隔離系統.對比分析了有無限位裝置的準零剛度系統在半正弦沖擊載荷作用下的相對位移響應及加速度響應,研究了限位式準零剛度系統在不同限位器參數(剛度比、阻尼比)下的沖擊響應特性,為之后合理設計具有抗沖擊性能的低頻隔離系統提供理論參考.
1 限位式準零剛度隔離器
1.1 物理模型
圖1為限位式準零剛度隔離系統的簡化模型,主要由三彈簧準零剛度隔振系統與限位裝置并聯而成.其中,構成準零剛度系統負剛度結構的是剛度為kh的水平雙壓縮彈簧,其原長為l0,壓縮后長度為l;正剛度結構是剛度為kv的豎直彈簧,阻尼為c1;k2和c2代表限位系統剛度和阻尼;M為被隔離設備的質量;限位器為雙向限位,Gap為限位器單側間隙,設限位器上側間隙為正值,下側間隙為負值;x為系統的位移響應.在重力作用下,此時系統處于靜平衡位置,兩側彈簧kh處于水平壓縮狀態.準零剛度隔振系統的上下兩端分別與被隔離設備和基座相連,起到支撐和隔振作用.當準零剛度隔振器變形超過單側間隙時,限位器與設備接觸,限制設備產生較大位移.

圖1 限位式準零剛度系統簡化模型Fig.1 Simplified model of limiter-type QZS system
1.2 工作原理

(1)

(2)
限位式準零剛度隔振器的力學模型如圖2所示,其中,虛線為無限位裝置的準零剛度隔振系統力學模型.x3與x2分別為限位器作動的上下節點.當x位于|x2x3|段內時,兩曲線重合,此時限位器未作動,系統具有準零剛度特性,一般情況下|ox2|=|ox3|=Gap.當x超過此段時,限位器發生作用.
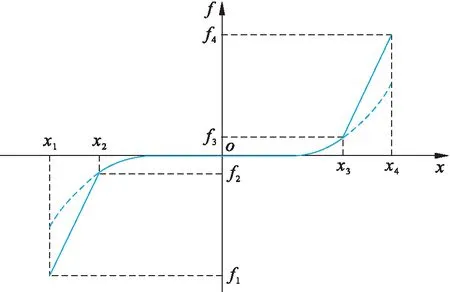
圖2 力學模型簡圖Fig.2 Schematic diagram of mechanical model
2 運動方程
在基底沖擊激勵的作用下,圖1所示的限位式準零剛度系統的運動方程主要分為兩部分,本文用z=x-y表示設備的相對位移.
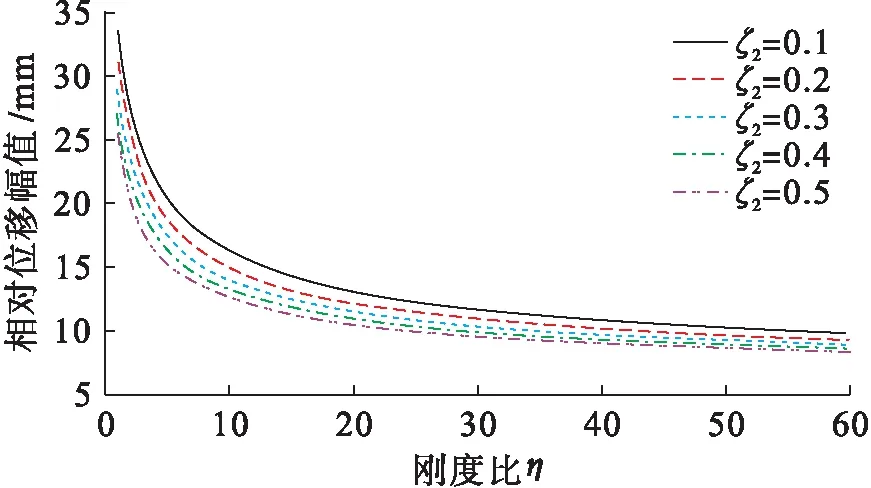
1) 當|z| 2) 當|z|≥Gap時,被隔離設備的相對位移大于限位器的安裝間隙,與限位器發生碰撞,此時系統的剛度k為準零剛度系統與限位系統的剛度之和,系統的阻尼為隔振器阻尼c1與限位器阻尼c2之和. 根據以上分析,限位式準零剛度隔振系統在沖擊激勵作用下的運動方程為 (3) (4) 其中:A為沖擊載荷加速度幅值;t0為沖擊持續時間;fs=1/t0為沖擊頻率. (5) (6) (7) 根據已確定的隔離器參數,選取沖擊載荷加速度幅值A=50g,脈寬t0=5 ms,g=9.8 m/s2.取限位器兩側限位間隙為5 mm,限位器的阻尼比為ζ2=0.05,剛度比為η=8.系統的相對位移響應及加速度響應曲線分別如圖3、4所示.其中,限位系統為圖1所示的限位式準零剛度隔離系統;準零系統為無限位器的三彈簧準零剛度系統;線性系統為準零系統去掉負剛度結構后的等效線性系統. 圖3 相對位移響應曲線Fig.3 Relative displacement response curves 由圖3可以看出,三個系統中設備的相對位移最大峰值均出現在沖擊結束后的第一個峰值處,其中,準零系統的最大峰值出現在0.047 8 s處,峰值為48.67 mm;線性系統的最大峰值出現在0.044 2 s處,其峰值為39.76 mm,相對于準零系統降低18.3%;限位系統第一個峰值出現在0.019 8 s,其峰值為18.41 mm,相較于未安裝限位器的準零系統,其峰值降低62.2%,相對位移響應峰值大幅降低. 圖4 加速度響應曲線Fig.4 Acceleration response curves 由圖4可以看出,限位系統的加速度響應明顯增加,其峰值出現在0.018 7 s,峰值為15.34g,是準零系統加速度峰值的2.3倍.同時可以看出,由于限位器壓縮時吸收能量,恢復變形時釋放能量,使系統受到的沖擊能量更快耗散,限位系統的加速度響應更快趨于平穩. 通過對比可知,限位器的加入使相對位移響應得到明顯降低,有效限制設備在沖擊激勵下產生較大位移,同時加速度響應急劇增加.匹配合理的隔離器參數,既使相對位移有效降低,又可以獲得相對較低的加速度響應. 限位式準零剛度系統在半正弦沖擊載荷作用下,分別選取不同的限位器阻尼比ζ2(0.03~0.57)和剛度比η(1~60).限位器阻尼比ζ2與剛度比η對限位式準零剛度系統相對位移響應峰值的影響規律如圖5、6所示. 圖5 不同剛度比下相對位移幅值隨阻尼比變化曲線Fig.5 Curves of relative displacement amplitude in relation with damping ratio under different stiffness ratios 由圖5可以看出,當系統的剛度比η為定值時,設備的最大相對位移隨限位器阻尼比ζ2的增大而減小,且η較小的設備對阻尼比ζ2更加敏感.同時結合圖6可以明顯看出,當阻尼比ζ2為定值時,相對位移幅值隨著剛度比的增加而逐漸衰減,當η<10時衰減迅速,隨剛度比逐漸增大衰減趨勢逐漸變緩. 圖6 不同阻尼比下相對位移幅值隨剛度比變化曲線Fig.6 Curves of relative displacement amplitude in relation with stiffness ratio under different damping ratios 限位器阻尼比ζ2與剛度比η對限位式準零剛度系統加速度響應峰值的影響規律如圖7、8所示. 圖7 不同剛度比下加速度幅值隨阻尼比變化曲線Fig.7 Curves of acceleration amplitude in relation with damping ratio under different stiffness ratios 圖8 不同阻尼比下加速度幅值隨剛度比變化曲線Fig.8 Curves of acceleration amplitude in relation with stiffness ratio under different damping ratios 由圖7可以看出,當剛度比η為定值時,加速度幅值隨阻尼比ζ2的增加呈現先減小后增大的趨勢.為了更加清晰地反應出峰值變化的規律,將不同剛度比η對應的加速度響應峰值的極小值點設為a,將a點所對應的阻尼比設為ζa,并將這些極值點連接起來,如圖7中的曲線α所示.對于加速度響應來說,較大剛度比η的設備對阻尼比ζ2的變化更加敏感.結合圖8可以看出,系統加速度響應峰值與剛度比η呈正相關,且增加趨勢逐漸變緩. 綜上所述,當限位器剛度較大時,其相對位移幅值較小,適當減小限位器的阻尼比,可減小其加速度響應幅值;當限位器剛度較小時,其加速度響應幅值較小,此時適當增加其限位器的阻尼比,可以減小相對位移的響應幅值.通過匹配合理的限位器參數既可獲得較低相對位移響應,同時系統的加速度響應也可顯著減小,有效提升系統的抗沖擊性能. 本文通過分析得出以下結論: 1) 相較于無限位的準零剛度系統,限位式準零剛度隔離系統在沖擊載荷作用下可有效降低系統的相對位移響應峰值,且該系統在平衡位置附近仍具有準零剛度特性. 2) 在小阻尼比范圍內(0<ζ2<ζa),增大限位器的阻尼可降低設備的相對位移響應幅值和加速度響應幅值;當阻尼比較大時(ζa<ζ2),相對位移響應幅值繼續降低,但加速度響應幅值會隨之增大. 3) 限位器剛度比的增加可有效降低系統的相對位移響應幅值,但會導致加速度響應幅值增大. 4) 對于大剛度比限位器而言,系統的相對位移響應較小,適當減小限位器的阻尼比,可減小其加速度響應幅值;小剛度比限位器的加速度幅值較小,此時適當增加其限位器的阻尼比,可降低其相對位移的響應幅值.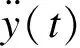
3 沖擊響應計算及分析

3.1 限位器對沖擊響應的影響


3.2 限位器參數對沖擊響應的影響



4 結 論

