SD振子的Hopf分岔研究*

王翠艷,王明昊

(石家莊鐵道大學，河北 石家莊 050043)

0 引言

振動現象在許多工程應用中都是有益的，如攪拌、低能量導航和控制、機電系統的監測和故障診斷等。通過控制策略產生Hopf分岔[1]是一種將有具體振動特性的系統設計為非線性動力學系統的方法，Hopf分岔自身則是一種從非雙曲平衡點中產生極限環分岔的現象。PB(Poincaré-Birkhoff)規范型理論常被用于從解析角度研究Hopf分岔[2，3]。Li等[4]研究了含有雙時滯參數的Lengyel-Epstein系統的Hopf分岔，使用時滯微分方程的規范型理論與中心流形定理，得到了確定周期解穩定性與Hopf分岔方向的顯式表達式。Zhang等[5]研究了水下滑翔機姿態控制系統中由時滯引發的Hopf分岔現象，得到了產生Hopf分岔的臨界時滯條件。Li等[6]研究了一類兩物種共棲系統的Hopf分岔與穩定性。Zhang等[7]研究了一類時滯傳染病模型的Hopf分岔與穩定性，使用規范型理論與中心流形定理得到了Hopf分岔方向與周期解分岔穩定性的顯式算法。Somnath R等[8]研究了雙簡諧激勵作用的雙穩態van der Pol-Mathieu-Duffing系統的超臨界Hopf分岔現象。

本文研究了SD(Smooth and Discontinuous)振子彈簧處于預拉伸狀態時平凡解鄰域內的Hopf分岔。使用多尺度法，得到了同時含有非線性黏性阻尼和簡諧激勵的平均系統。基于PB規范型理論，得到了Hopf分岔條件并研究了極限環的穩定性。隨后使用上述方法，研究了系統彈簧處于預壓縮狀態時非平凡解鄰域的Hopf分岔。

1 SD振子的Hopf分岔

近期的文獻提出了可以實現光滑至不連續系統演化的SD振子，模型如圖1所示。其中,x表示振子位移，l表示振子位移路徑至彈簧固定點的距離(半跨距離)，其無量綱無擾動的運動微分方程為：

(1)

其中：α為系統光滑參數，0<α<2。

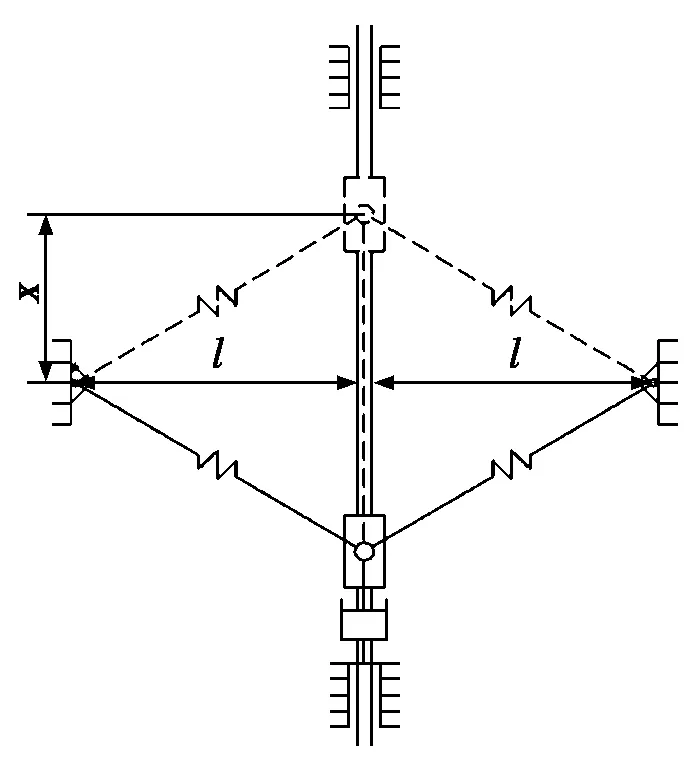
圖1 SD振子系統

該系統可以通過調整光滑參數α的值，實現從光滑系統到不連續系統的演化。當α=0時，其表現出不連續動力學行為[9,10]，此時系統的半跨距離l=0，導致系統實際上難以實物化。當α>0時，系統表現出光滑動力學行為。當α=1時，該系統對應具有余維2分岔現象的單自由度弦振動模型。如文獻[11]所示，當α>1時，該系統類似于一個預拉伸的離散彈性弦。

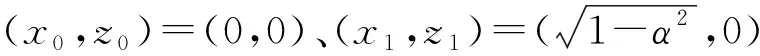
假設系統(1)受非線性黏性阻尼f(x)=ξ+γx2和一個幅值為F0、頻率為Ω的簡諧激勵擾動。此時，該受迫耗散系統可以表示為:

(2)

其中：為了表示廣義非線性阻尼且不失一般性，ξ、γ可以取為任意實數；t為擾動時間。

為了得到平衡點(0,0)附近的平均方程，使用多尺度法，系統(2)可以改寫為：

(3)

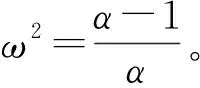
設ε是一個小尺度擾動參數，取變換：

(4)

將式(4)代入系統(3)，整理后可得:

(5)

假設系統(5)的解x可以由多個時間尺度表示：

x(t,ε)=x0(T0)+εx(T0,T1)+
ε2x(T0,T1,T2)+….

(6)

其中：Ti=εit,i=0,1,2,…。

根據多尺度法，定義微分算子如下:

(7)

(8)

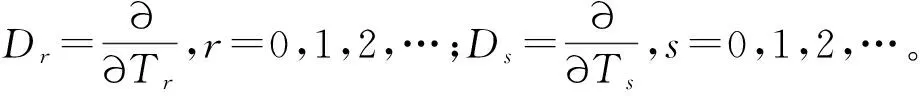
下面，重點研究系統產生1∶2內共振的情況。這種共振情況下，存在如下頻率關系:

(9)

其中：σ為調諧參數。為了便于分析令Ω=2。因此:

ω2=1+εσ.

(10)

將式(6)～式(10)代入系統(5)，令方程左側和右側的ε同冪次系數相等，可得:

ε0時：

(11)

ε1時：

(12)

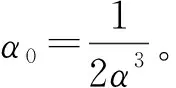
系統(11)的1次近似復數解的形式可以表示為:

(13)

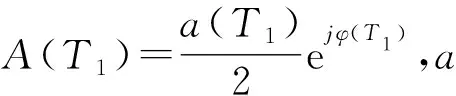
將式(13)代入系統(12)，可得：

(14)

其中：cc為系統(14)右側函數的共軛；NST為不包含久期項的部分。

為了消除系統(14)中的久期項，由式(14)可得:

(15)

A可以表示為笛卡爾形式:

A=y1+jy2.

(16)

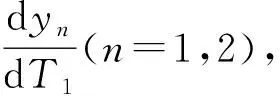
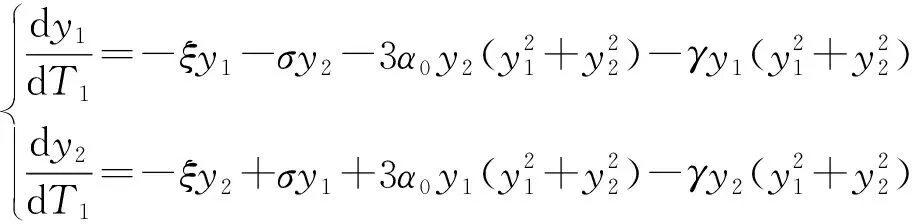
(17)

顯然，(y1,y2)=(0,0)是平凡解，系統(17)為ξ=0時的PB規范型。系統(17)線性化導算子的特征值為:

λ1,2=-ξ±jσ.

(18)

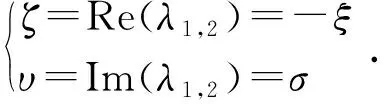
(19)

根據Poincaré-Andronov-Hopf定理，可得:

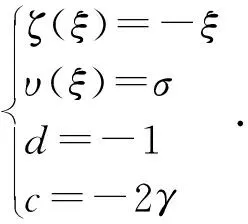
(20)

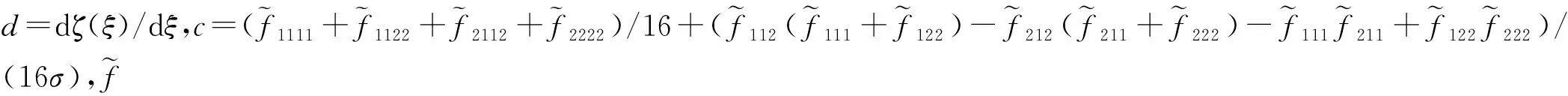
結合式(20)和文獻[3,4]，可以通過ζ、υ、d和c的值來判斷奇點的類型與極限環的穩定性。

2 結果分析

研究各種參數情況下式(20)的結果，可得系統(2)的奇點類型與極限環穩定性。使用MATLAB對系統(2)進行數值模擬，結果如圖2～圖4所示。

(1) 當γ<0時，對于ξ<0該平凡解是一個不穩定焦點，ξ>0時其為一個漸進穩定焦點，并且存在一個不穩定極限環。當γ<0時，出現亞臨界Hopf分岔，如圖2(a)所示。

(2) 當γ>0時，對于ξ>0該平凡解是一個漸進穩定焦點，ξ<0時其為一個不穩定焦點并且存在一個漸進穩定的極限環。當γ>0時，出現超臨界Hopf分岔，如圖2(b)所示。

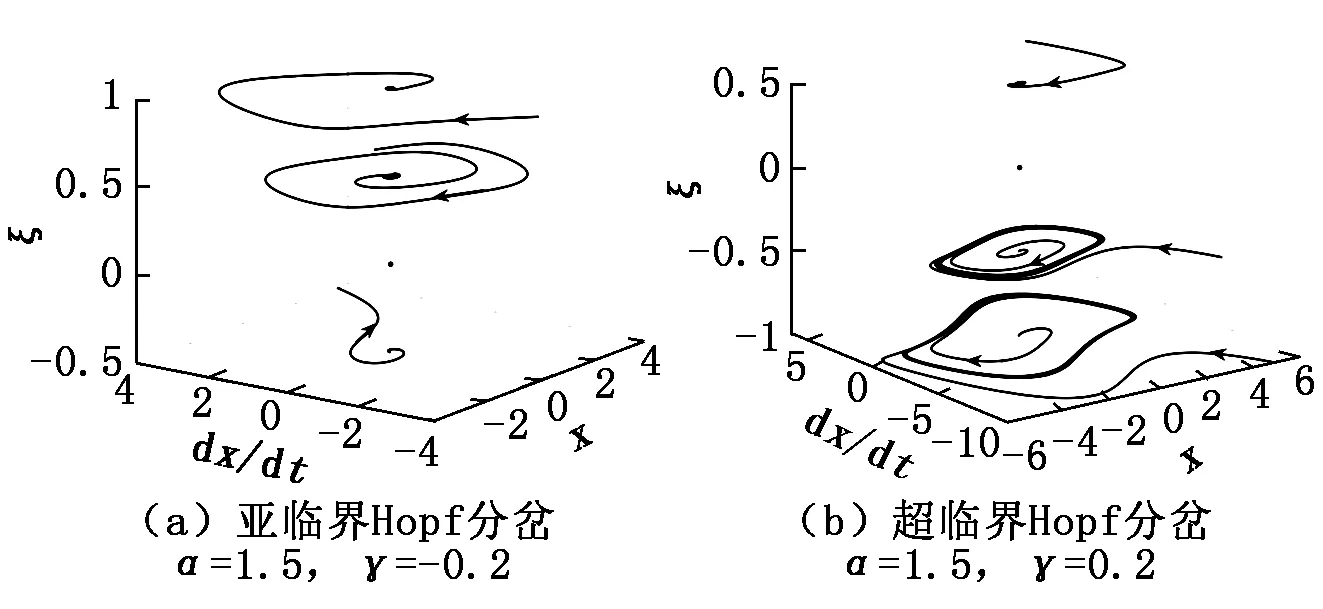
圖2 系統(2)在平衡點(0,0)鄰域的Hopf分岔

圖3 系統(2)在平衡點鄰域的Hopf分岔

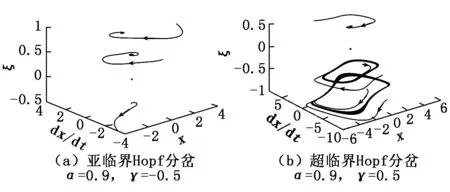
圖4 系統(2)在平衡點鄰域的Hopf分岔

圖2(a)、圖3(a)和圖4(a)分別描述了ξ變化時亞臨界Hopf分岔現象。圖2(b)、圖3(b)和圖4(b)描述了超臨界Hopf分岔。圖2～圖4中亞臨界Hopf分岔與超臨界Hopf分岔對應的參數情況與式(20)結果一致，這表明解析解與數值計算結果一致，1∶2內共振條件下SD振子Hopf分岔定性分析結果正確。

3 結論

本文針對SD振子，研究了系統的超臨界、亞臨界Hopf分岔及其穩定性。從平衡點研究出發，探討了平凡平衡點、非平衡點鄰域的復雜非線性動力學行為。利用多尺度法求得系統平均方程，探討了平凡平衡點、非平衡點鄰域的超臨界、亞臨界Hopf分岔。利用PB規范型理論分析了所有平衡點極限環分岔的穩定性。進一步地，利用數值模擬的結果驗證了解析結果的正確性。