順“理”成“章”：學習近似數的支點

江蘇南京市百家湖小學（211100）張麗莉

蘇教版教材二年級下冊第三單元“認識近似數”是在學生學會了萬以內數的大小比較基礎上編排的，通過引導學生思考兩個學校的學生人數分別接近幾百人，初步體會比700多一些或少一些都是接近700，在此基礎上認識“約等號”及其表示方法。隨后的“試一試”是引導學生在感受一個四位數接近幾千的基礎上，嘗試用“≈”表示大約幾千，進一步感受一個數的近似數。

【課前思考】

這是一節繼“多得多、多一些、少一些、少得多”之后的“生長課”，也是學生后續學習“四舍五入求近似數”的種子課。需要思考以下兩個問題：

1.如何讓學生體會接近整百、整千的數？從年段的教學內容看，之前的一年級有百數表，學生通過填寫完整的百數表能感受數與數之間的遠近及大小關系。那么如何讓學生感受三位數與四位數？從本單元的編排體系看，一開始就是“認識萬以內的數”，通過數一數感受萬以內數的順序，通過說一說掌握萬以內數的組成，這些都是學習萬以內數的大小比較的基礎，同時也是認識一個數的近似數的基礎。

2.如何建立近似數的概念？如何從一個數的近似數拓展到近似數的范圍？僅僅按教材的例題教學，顯然不夠，需要教師對教材進行再挖掘。

《義務教育數學課程標準（2011年版）》指出：數學教學活動必須建立在學生的認知發展水平和已有的知識經驗基礎之上。結合以上對教學知識點的思考，筆者不由得想：何不像郭橐駝種樹一樣，順應天性，找準學生的認知起點，讓學生真實經歷近似數的理解過程，水到渠成地走向更深入的學習？

【教學過程】

教學片段1：通過數數感受數的大小關系。

出示要求：

（1）一千一千地數，7000前面一個數是（ ），后面一個數是（ ）。

（2）一百一百地數，7000前面一個數是（ ），后面一個數是（ ）。

（3）十個十個地數，7000前面一個數是（ ），后面一個數是（ ）。

（4）一個一個地數，7000前面一個數是（ ），后面一個數是（ ）。

師：看到這些，你有什么想說的嗎？先獨立思考，再與同桌交流，最后全班交流。

生1：都是在找7000前面的數和后面的數。

生2：數的方式不一樣，有的是一千一千地數，有的是一百一百地數。

生3：都是在找與7000相鄰的數。

生4：我發現從第（1）題到第（4）題，填的數越來越接近7000。

生5：是的，因為數的間隔越來越小。

【反思：數數是學生學習數學的開始方式。在最初數10以內的數時，學生在數數的過程中感受數的大小，繼而理解相鄰數的含義以及“接近”的意義。當認識的數的范圍不斷擴大時，學生也在數數的基礎上認識整十、整百、整千數的大小關系。近似數是與準確數相近的數，通過數數能夠體驗“相近”以及“相近”的程度，為學習近似數做準備。】

教學片段2：理解大約7000的范圍。

師：還有哪些數接近7000呢？

生1：7001。

生2：我覺得7010也接近7000，6990也接近7000。

生3：我覺得7100也接近7000，6900也接近7000。

師：到底哪些數接近7000呢？

生4：我覺得6500到7500之間的數都接近7000。

師：其他同學能聽懂生4的意思嗎？

（大部分學生搖頭）

生5：我可以把他的意思用圖表示出來（如圖1）。

圖1

生6：看圖后我懂了，靠近7000的數，有的在7000的前面，有的在7000的后面。

生7：我也知道了，有的比7000少一些，有的比7000多一些。

生8：其實就是這個范圍內的數都接近7000。

師：為什么是這個范圍內的數都接近7000呢？請小組討論。

生9：從這個數軸上看，再往前數最大是6499，它與6000相差499，但是它與7000相差501，所以6499離6000近一些，離7000遠一點。

生10：按生9說的意思，從7000往后數，到7500之間的數都接近7000，再往后就接近8000了。

生11：現在我真正看懂這幅圖了，我覺得6500到7500之間的數都接近7000。

師：能畫出接近8000的數嗎？

學生畫圖：

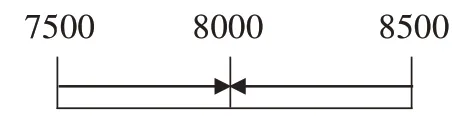
圖2

師：對于接近8000的數，我們就說，這些數的近似數是8000。

師：哪些數的近似數是800呢？

生12：750到850之間的數的近似數都是800。

師：哪些數的近似數是80呢？

生13：75到85之間的數的近似數都是80。

【反思：以“哪些數接近7000”為核心問題，引導學生自主構建“求一個大數目的近似數時應根據省略部分最高數位上的數字進行判斷”這一認知難點。本環節主要分三個層次：第一次是“任意說”，對于“哪些數接近7000”這個問題，很多學生說出的都是十分接近7000的數，這是對數的遠近關系的直覺，但學生往往不敢說比7000小（或大）得多的數。第二次是“引導說”，借助學生畫出的數軸，引導學生直觀感受與7000近似的數的特點。學生的學習水平各有高低，有的學生已經學會了概括與總結，有的學生還停留在“不會”的層面，此時可以安排學生間的交流互動活動。通過小組討論比較相差數，學生能理解為什么這些數接近7000。雖然本節課不要求學生能用“四舍五入”法求出近似數，但需要學生理解“為什么這些數的近似數是7000”，而借助數軸的直觀化顯示功能能滲透“四舍”和“五入”的合理性。第三次是“遷移說”，在學生理解了哪些數的近似數是7000或8000以后，緊扣數軸的直觀性，讓學生自主遷移到問題“哪些數的近似數是800？哪些數的近似數是80？”。這樣的遷移能夠再次讓學生領會近似數的含義。】

【課后反思】

對近似數的認識是學生第一次從模糊的感知到數學上的理性表達。在之前的生活經驗與數學學習中，學生接觸的都是準確數，雖然生活中接觸過“大概”“差不多”，但是用數學符號表達，這是第一次。回顧以上教學過程，筆者得出結論：只有順應教材的編排體系，找準學生的認知起點，設計有效的問題引領，才能讓近似數的學習順“理”成“章”。

1.順教材的靜態之“理”——循序漸進成文本的結構之“章”

翻閱一年級和二年級的教材后不難發現，教材在編排一年級10以內數的認識時已經為“認識近似數”埋下伏筆。在“認識7、8、9”后編排了一道練習（如圖3），學生借助學習工具——直尺，感受5與8、1的大小關系，這為后續認識“多一些，少一些”奠定了基礎。在認識了20以內數及組成以后教材也編排了相應的練習（如圖4）——將直觀的尺子變成了抽象的數線，且每一小段表示一個數（一個一個地數），學生看著數線回答問題，感悟數與數之間的距離，得出數的大小關系。這里的“接近10還是20？”是第一次出現如何判斷接近整十數。教材在一年級上冊的期末復習題中將20以內的數在兩條數線中以填空的形式表現出來（如圖5），這是鞏固與復習，同時讓學生感受數的大小順序。教材在一年級下冊“百數表”和“多一些、少一些、多得多、少得多”后安排了相應的練習（如圖6），這時的接近數已經變成了整百數100。隨著學生對數的認識的范圍不斷擴大，教材對“接近”的范圍不斷擴充，在之后的單元復習中也安排了整十數之間的遠近比較（如圖7），這次的數線的每一段并不是只代表一個數，還可以表示十個數，學生對數線的認識又進了一步。

圖3

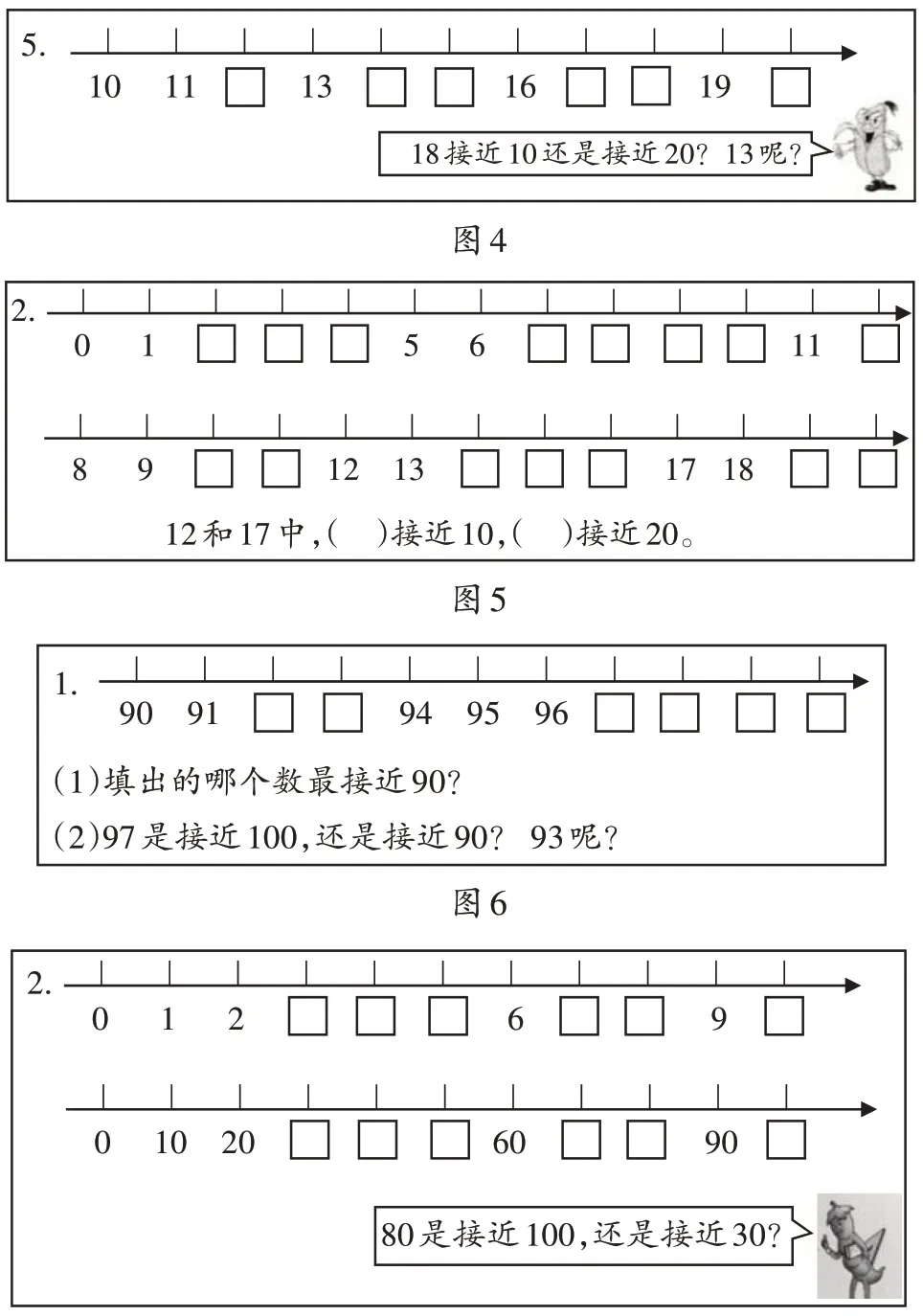
圖7

教材的編排是循序漸進地滲透“接近”的內涵，從直觀的實物直尺到抽象的數線，再到用數線表示不一樣的數。厘清教材編寫的靜態之“理”，也就理解了“近似數”對學生后續學習的重要性。可見，“近似數”的學習具有承上啟下的作用，唯有順應教材編排的脈絡，才可以讓近似數的教與學“有章可循”。

2.順學生的動態之“理”——自然生發成學的結構之“章”

認識近似數前，學生的學習起點在哪里？基于之前的學習，學生有萬以內數數的經驗，也掌握了萬以內數的大小比較。不同方式的數數，結果各不相同，但是卻能促使學生感知數與數之間的距離，其歸納的過程也是學生思維進階的過程。鄭毓信教授說：“數學教育的一個主要目的就是幫助學生學會思維，并能逐步學會想得更清晰、更全面、更深刻、更合理。”有了數與數的遠近感知，再找大約7000的數的范圍，似乎已是水到渠成。教學過程中學生主動概括出大約7000的范圍，甚至用圖示表示這一范圍，這是意外還是巧合？筆者認為均不是。實際上，正是學生有了之前對“接近”一詞的深刻理解，還有對數線潛移默化的認知，才會自發地想用圖示表達。不僅如此，由近似數是7000的數自主遷移到近似數是8000的數，再拓展到近似數是800和80的數，學生的思維一下子打開了，不限于對近似數為整千數的理解，還擴展到整百數、整十數，呈現“由線到面”的結構化學習。

史寧中教授說過：數學學習的最終目標，是讓學習者會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界。掌握學生認識近似數的過程，找準知識的起點與生長點，以“聯系”為紐帶，以“貫通”為路徑，讓這一知識的學習呈現結構化，其意義不僅在于促進學生的認知、理解與掌握，更重要的是引領學生自主遷移和靈活運用。

3.順教師的無為之“理”——潤物無聲成教的結構之“章”

教與學永遠都是相輔相成的。教師的主導作用要基于“確保沒有一個人是‘教育上的不利者’，并確保所有學生都有最充分地運用自己的潛能的平等機會”。教師在教學中既要把握知識的內在結構，更要尊重學生的認知規律，以實現“知識序”與“認知序”的有機統一，從而實現“教學序”的有效呈現。教學中教師沒有過多的教學語言，而是通過兩個簡單的核心問題引發學生思考。在輔助學生順利走進“最近發展區”的數數活動中，當學生用不同方式數數后，教師先以“你有什么想說的？”引發學生觀察、比較，“語言是思維的外殼”，學生將數數的感受表達出來，體現數學思維的提升；教師再用“還有哪些數接近7000？”激發學生自主用數線圖表示大約7000的范圍。教師的看似“無為”成就了學生的“有為”。

葉瀾教授說：“課堂是一種生活，如何讓課堂上的學生積極、主動地展現生命的活力，是我們需要研究和反思的。”無論是教材的靜態之“理”，還是學生的動態之“理”、教師的無為之“理”，都要經過一段時間的孕育，才能彰顯生命的和諧統一！