塔式起重機鋼結構腐蝕損傷宏觀表征研究

宋世軍 彭振飛 馬 磊 王忠雷

山東建筑大學機電工程學院 濟南 250101

0 引言

塔式起重機（以下簡稱塔機）是建筑行業不可或缺的大型起重設備，其主要承載結構件采用金屬材料，其自身的腐蝕磨損不容忽視，有的塔機在具有腐蝕性的環境中使用，作業環境非常惡劣。雖然在一般情況下塔機鋼結構會進行防腐處理，但隨著時間的推移，防腐層會從一些薄弱位置（如連接處、構件根部處）開始失效，進而使鋼材發生腐蝕，造成嚴重后果。為確保塔機的正常運行，對其鋼結構不同腐蝕情況所造成的影響進行預測具有重要意義。

李斌等[1]以損傷力學為基礎建立了缺口構件的損傷演化方程，并用新的模型預估了不同應力集中系數時的疲勞壽命；陳志華等[2]采用實驗和Abaqus軟件分析了不同因素對桿件軸壓力學性能的影響；梁彩鳳等[3]通過試驗點獲得不同鋼材的大氣暴露腐蝕試驗數據，驗證了鋼的大氣腐蝕發展規律；賈晨[4]等通過對國內外研究現狀總結得出腐蝕失重是最常用的腐蝕損失指標；高貝等[5]采用模擬和實驗方法研究了不同凹陷深度對鋼管應力應變的影響；李天奇等[6]模擬計算了由于不同尺寸腐蝕坑導致的不同應力腐蝕對抽油桿壽命的影響。

目前針對于整個腐蝕過程及局部腐蝕對整體結構的影響研究較少，且大多為損傷力學或是對發生腐蝕損傷處進行應力分布狀況的研究。鑒于此，本文采用理論分析與數值模擬相結合的方法，以80塔機為例，使用Ansys APDL命令流建立多尺度模型，對局部進行自然腐蝕及自然腐蝕之后的應力腐蝕進行模擬。通過標準節損傷主肢頂端特征點沿起重臂方向位移的變化即宏觀表征，來研究腐蝕不同階段下不同參數對其影響，以期為塔機的安全風險評估及壽命預測提供參考與借鑒。

1 腐蝕理論模型

Kachanov在1958年提出用連續度來描述材料的逐漸衰變[7]，考慮到一均勻受力的梁，材料的主要劣化機制為有效橫截面積的減小[8]，即有

式中：δS為無損時的承載橫截面積，δSD為損傷失效的橫截面積。

當D＝0時，即為沒有損傷的理想材料；當D＝1時，即為材料疲勞破壞時產生裂紋或斷裂破壞。材料的有效應力為

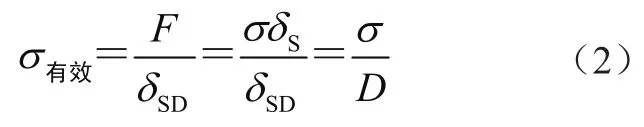
式中：σ有效為材料的有效應力，F為外加載荷，σ為柯西應力。

由式（2）可知，材料有效應力隨連續度的減小而增大，即當連續度D達到某一臨界值Dc時，材料產生疲勞破壞，故材料疲勞破壞條件為

以損傷本構模型為基礎，分析材料的腐蝕損傷機理，腐蝕損傷可分為自然腐蝕及自然腐蝕之后的應力腐蝕，圖1為腐蝕損傷下的模式圖。

圖1 腐蝕損傷模式圖

由文獻[9，10]可知，在外界環境相同時，由腐蝕而引起成的局部材料損失率即連續度D的大小關系與腐蝕時間呈正比，與腐蝕后所受應力呈反比，基于此規律，自定義一個材料損失系數α，即有

2 Ansys模型的建立

使用Ansys建立三維模型，采用3節點3D線性單元Beam 188，平衡臂及起重臂與塔帽相連接的拉桿采用3D有限應變桿Link 180單元，平衡重、變幅小車、吊鉤選擇質量單元Mass 21，實體部分采用8節點實體單元Solid 185。

選擇塔機標準節主肢1底端作為損傷位置，建立實體模型模擬鋼的自然腐蝕及應力腐蝕。選取標準節主肢1頂端7 454點作為特征點，研究不同損傷情況下該點沿起重臂方向位移的變化情況（即宏觀表征，見圖2）。起重臂臂端加載起升載荷階段如圖3所示。

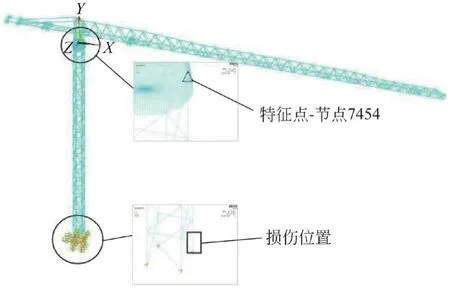
圖2 損傷位置特征點位置

圖3 起重臂臂端加載示意圖

3 損傷數值模擬

3.1 自然腐蝕模擬

通過文獻[3]所得鋼的大氣腐蝕規律h＝Atn，以北方某地區數據為例，代入A3的數據得到A＝0.03；n＝0.42，計算得到北方某地區50 a因自然腐蝕所造成的鋼材外層壁厚損失，使用Ansys進行模擬。

其中，t為自然腐蝕時間，h為因自然腐蝕所造成的壁厚損失量，D為連續度，MM為在起升工況下標準節主肢1頂端特征點完好與損傷情況下位移差值最大值的絕對值。將時間t與壁厚損失量h進行曲線繪制，如圖4a所示。該曲線的趨勢與忽略自然腐蝕損傷的不均勻性、自然腐蝕速率將趨于常數的理論結論相符合。

圖4 自然腐蝕階段模擬

對圖4b曲線進行三次冪函數擬合可得

令MM"（D）＝0，得到D＝0.992 653 34，即該函數圖像的拐點。由此可知，在自然腐蝕情況下特征點的位移差值變化較小，當連續度D＜0.992 653 34時，自然腐蝕時間介于25～30 a時主肢頂端特征點的位移差值變化更明顯。

然而，在不同地區由于環境因素的影響會對結果造成較大影響，以南方某地區為例，根據文獻[12]，繪制變化曲線如圖5所示。

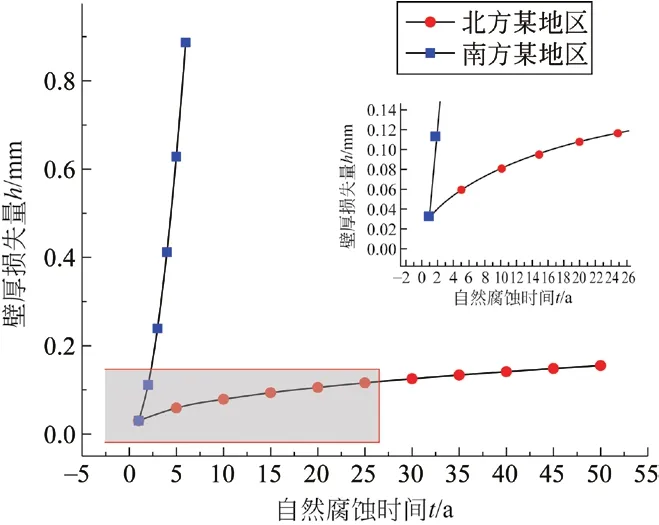
圖5 時間-壁厚損失率變化曲線

由圖5可知，南方某地區在自然腐蝕第2年時的厚度損失量即可達到北方某地區變化的拐點。

3.2 應力腐蝕模擬

1）腐蝕坑階段的模擬

在構件根部建立實體模型，由文獻[9]無腐蝕坑時應力腐蝕可忽略這一結論，使用Ansys模擬應力腐蝕初期出現腐蝕坑的階段，分別研究腐蝕坑數量和深度因素對特征點位移差值的影響。

選取根部實體部分上下端位置作為腐蝕坑的位置處，模擬缺陷深度為2 mm時腐蝕坑數量的變化對特征點位移差值的影響，所得結果如圖6所示。

圖6 腐蝕坑數量-特征點宏觀表征變化曲線

由圖6可知，二者趨勢大致相同，差距隨載荷步的增加逐漸明顯，取不同位置曲線的最大值得到圖7所示結果。由圖7可知，下端腐蝕坑相比于上端對特征點宏觀表征影響更大。

圖7 最大位移差與腐蝕坑個數關系

模擬腐蝕坑個數分別位于上下端位置，缺陷深度分別為2 mm、4 mm、6 mm、8 mm、10 mm時，隨著腐蝕坑缺陷深度的增加對特征點位移差值的影響，所得結果如圖8所示。

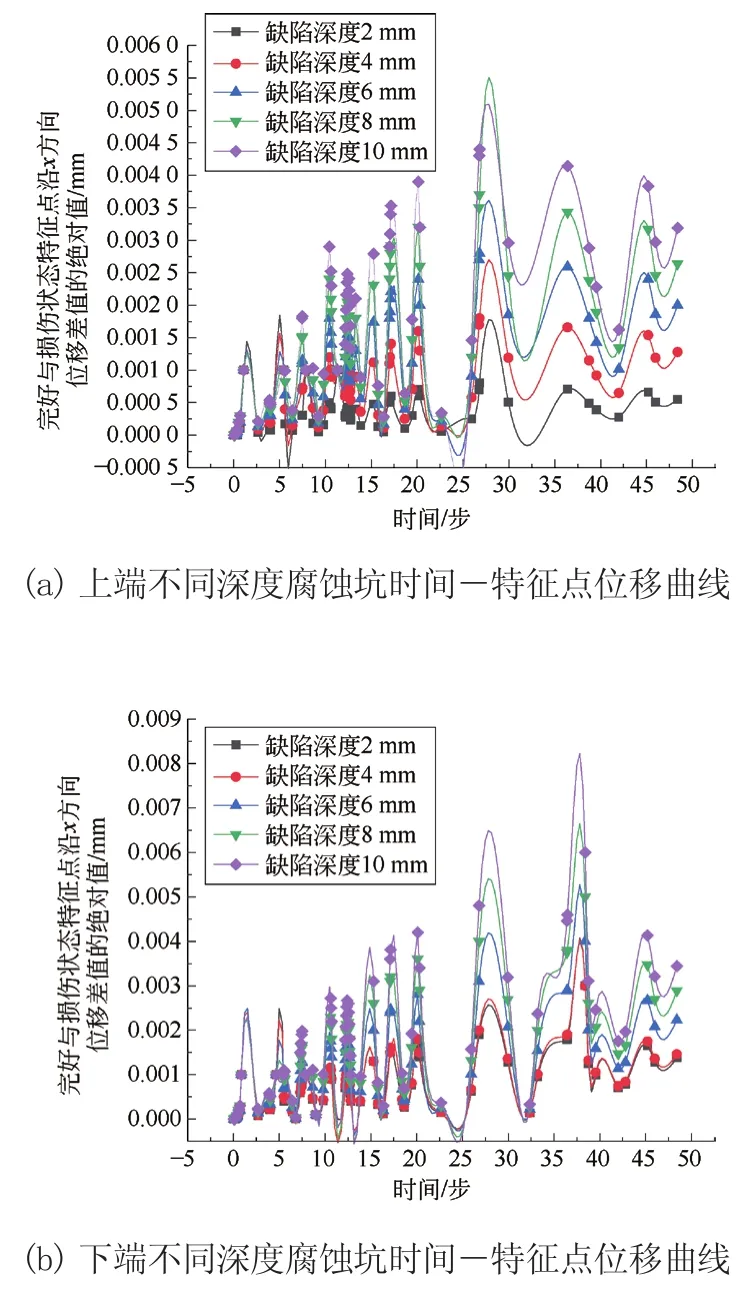
圖8 腐蝕坑深度-特征點宏觀表征變化曲線

由圖8可知，隨著腐蝕坑位置從上端到下端，在時間步的后期，上端腐蝕坑時間步-特征點位移變化曲線更加平滑。

綜合圖7b和圖8b可知，在下端應力較大位置處，腐蝕坑的深度相較于數量對特征點處振動的頻率變化有較大影響，取不同位置曲線最大值得到圖9所示結果。

圖9 最大位移差與腐蝕坑深度的關系

由圖9可知，腐蝕坑深度相較于腐蝕坑數量對特征點位移差值的影響較大，下端相較于上端位置腐蝕坑對宏觀表征的影響較大，隨著腐蝕坑深度的增加2條曲線趨于一致。

分析以上2種不同情況可知，同一位置腐蝕坑個數的增加或腐蝕坑深度的增加對標準節頂端特征點位移差值有疊加效果；不同位置腐蝕坑，隨著向應力較大處靠近，對標準節頂端特征點位移差值的影響逐漸增大。

2）腐蝕開裂階段的模擬

由文獻[8]可知，當某一位置的材料受損，其在應力作用下會從應力腐蝕中的腐蝕坑階段轉變為腐蝕裂紋。在下端分別模擬橫向裂紋和縱向裂紋，觀察不同路徑的腐蝕裂紋對特征點位移差值的影響，取腐蝕斷裂面積作為自變量，特征點完好與損傷狀態下位移差值作為因變量。其中，每層缺陷深度為2 mm，缺陷深度由外層向內2層擴展，所得結果如圖10所示。

圖10 不同路徑及深度腐蝕斷裂-特征點位移差值曲線

由圖10可知，當腐蝕外層時，橫向裂紋與縱向裂紋主肢頂端特征點位移差值較小，橫向裂紋對特征點位移差值的影響稍大。隨著腐蝕裂紋深度的增加，橫向裂紋與縱向裂紋對宏觀表征影響的差值逐漸拉開，橫向裂紋相較于縱向裂紋對特征點位移差值的影響逐漸增大。

4 結論

1）在自然腐蝕條件下，不考慮腐蝕的不均勻性對特征點位移差值影響較小。以北京地區數據為例，當連續度D＜0.992 653 34、自然腐蝕時間介于25～30 a時，特征點位移差值變化更明顯，但不同地區差距較大。

2）在自然腐蝕后的應力腐蝕中出現腐蝕坑的階段，同一位置腐蝕坑個數的增加或腐蝕坑深度的增加對特征點的位移差值有影響；不同位置腐蝕坑隨向應力較大處靠近，對特征點位移差值的影響逐漸增大，且應力較大處隨腐蝕坑深度的增加對特征點處的振動頻率有影響。

3）在應力腐蝕中的腐蝕斷裂階段，當腐蝕外層時，橫向裂紋與縱向裂紋主肢頂端特征點位移差值較小，橫向裂紋對于特征點位移差值影響稍大。隨著腐蝕裂紋向內層深度的增加，橫向裂紋與縱向裂紋對于特征點位移差值影響的差值逐漸拉開，橫向裂紋相較于縱向裂紋對于特征點位移差值的影響逐漸增大。