基于擴張觀測器的重載機械臂自適應魯棒控制
常景嵐,張高峰,曹秀芳,楊秀萍*,王收軍
(1.天津理工大學 天津市先進機電系統設計與智能控制重點實驗室,天津 300384;2.天津理工大學 機電工程國家級實驗教學示范中心,天津 300384;3.南京晨光集團有限責任公司,南京 210006)
0 引言
隨著科技水平的發展,機器人技術與我們的生活息息相關,而重載機械臂作為機器人的重要分支,憑借其可以大負載作業、人工成本低、生產效率高和安全等特點被廣泛應用在礦山機械、治金煉金等領域[1]。
為了提高機械臂的控制精度,學者們通過建立機械臂動力學模型,采用模型預測、自適應PID、神經網絡自適應、軌跡跟蹤自適應、滑模變結構以及魯棒自適應等控制策略[2~4]。電液伺服系統作為機械臂中重要的傳動系統,其中存在大量非線性特性和模型不確定性[5],文獻[6]聯合兩個觀測器與PID模塊作為控制器應用在兩關節機械臂,但未考慮機械臂變負載情況。文獻[7]采用自適應滑模法控制兩關節機械臂,但電液系統模型忽略了液壓缸的許多干擾因素。文獻[8]采用三階自抗擾控制方案應用在6自由度機械臂后臂液壓缸上,相對于傳統PID控制有了很大性能提升。
因此,本文針對重載機械臂電液伺服系統受摩擦影響大、變負載、存在不匹配干擾等特點,設計了一種基于擴張狀態觀測器的自適應魯棒控制器。其中,擴張狀態觀測器用于估計系統不匹配干擾并在控制器中前饋補償,自適應魯棒控制器通過參數自適應既保證系統具有良好穩態、瞬態性能,又減少了控制器對高增益反饋的依賴。
1 重載機械臂簡介
本文提及的重載機械臂包含7個自由度,其中3三個關節由液壓缸驅動,其余關節由液壓馬達驅動。通過SolidWorks對機械臂各零件建模,裝配完成后如圖1所示。其中,回轉馬達驅動機械臂主體在平面內做圓周運動;兩個俯仰缸驅動機械臂大臂俯仰運動;伸縮缸驅動機械臂腕部伸縮運動;平擺馬達實現機械臂腕部的左右擺動;進退缸、滾擺馬達和俯仰馬達分別驅動機械手做前后進退運動、左右滾擺運動和上下俯仰運動。
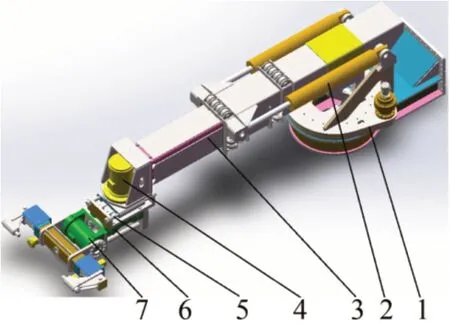
圖1 重載機械臂模型
2 電液系統模型的建立
限于篇幅原因,本文給出俯仰缸的數學模型,其他液壓缸和液壓馬達可根據各自數學模型應用本控制器達到相同控制效果。俯仰缸為單桿活塞缸,行程為795mm,速度為0~40mm/s,額定負載為227KN。由于重載和低速運動情況下系統的摩擦力影響是非常大的,本文采用Stribeck摩擦模型[9],對于造成的誤差以及其余未建模部分可以歸屬到不確定擾動中。Stribeck摩擦模型如下:

式(1)中:v為運動速度;B、Af、Fj分別為粘性阻尼系數、庫倫摩擦系數、最大靜摩擦力,vs為Stribeck速度,θ為經驗參數。
將Stribeck摩擦模型進行線性化[10]:

式(2)中:Fs為Stribeck摩擦參數。
俯仰缸電液伺服系統運動學方程為:

式(3)中:m為負載質量;y為液壓缸輸出位移;為p1、p2液壓缸左右兩腔壓力;A1、A2為液壓缸左右兩腔活塞的工作面積;Sf()、d(x,t)分別為類似于sgn(y˙)的可微連續函數、建模誤差和未建模部分。
對于液壓缸兩腔的壓力:

式(4)中:V1、V2分別為液壓缸左右兩腔實際容積;E為液壓油彈性模量;Ct為液壓缸泄露系數;pL=p1-p2為液壓缸左右兩腔壓差;q1、q2分別為伺服閥流入和流出液壓缸左右兩腔的流量。
假設1:伺服閥對稱匹配,伺服閥頻寬遠大于系統頻寬,則對于伺服閥流量有:


假設3:系統參考的指令信號x1d(t)三階連續有界。
3 含擴張狀態觀測器的自適應魯棒控制器
3.1 擴張狀態觀測器設計
將式(6)中的d(x,t)擴張為冗余狀態xe,并令xe=-d(x,t)/m,設計擴張狀態觀測器為:

3.2 控制器設計
定義如下不連續映射:

式(10)中:Γ>0為自適應增益,且為正定對角矩陣,τ為自適應函數。通過分析可知,參數的范圍可控,且相同于式(7)中φ的范圍,可得出如下性質:
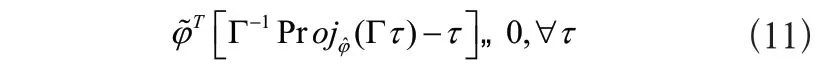
定義下面誤差變量:
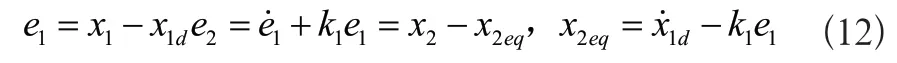
式(12)中:e1表示系統跟蹤誤差。
由式(6)、式(12)可得:

為了使e2趨于0,將x3看做式(13)中的一個控制輸入,并設計控制函數α2:

式(16)中:σ1為大于零的控制器設計參數;k2s2>0為非線性反饋增益[5]。
由e3定義以及式(6)得知:

式(18)中:k3s1為控制器參數,且k3s1>0;ua是模型補償項;ub為系統線性穩定反饋;uc為非線性反饋。
將式(18)代入式(17)可得:

選擇合適的uc從而滿足如下條件:

式(20)中:σ2為大于零的控制器設計參數;k3s2>0為非線性反饋增益[5]。
4 控制器性能及穩定性分析
設計參數k1,k2s1,k3s1,使下面矩陣Λ為正定矩陣:

令自適應函數τ=η2e2+η3e3,設計的控制器u具有如下性質:①系統中所有信號皆為有界信號。②經過某一時刻后,干擾準確估計,即?xe=0,則此時控制器u在保證結論①的同時,還可以獲得漸近跟蹤性能,即。
證明:對于性質①設置如下李雅普諾夫函數:

對式(22)中李雅普諾夫函數微分,結合式(12)、式(15)、式(19)可得:
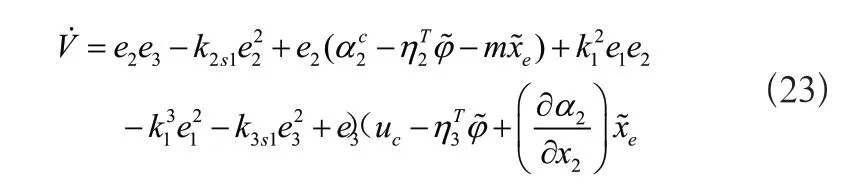
根據式(16)、式(20)和正定矩陣式(21)可得:

因此V有界,結合式(22)可證明性質①。
對于性質②,當?xe=0時,即=0,則可定義如下李雅普諾夫函數:


圖2 控制器結構框圖
5 仿真驗證

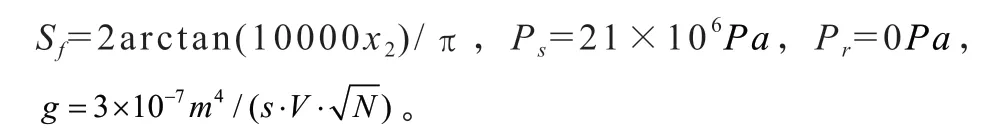
Stribeck摩擦模型如圖3所示。
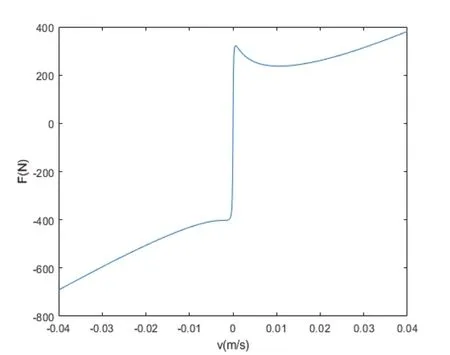
圖3 Stribeck摩擦模型
控制器參數參數如下:
1 )基于擴張狀態觀測器的自適應魯棒控制器(ESOARC):k1=2 5 0,k2s1+k2s2=2 6 0,k3s1+k3s2=80,Γ=diag[50,20,200,1×10-25] 1 ×10?25],φmin=[12000,450,1500,1×10-12],φmax=[13000,550,2500,1×10-11],φ(0)=[12000,450,1500,4×10-12],觀測器參數ω0=2000。
2)自適應魯棒控制器(ARC)。不包含干擾估計部分,系統參數與基于擴張狀態觀測器的自適應魯棒控制器相同。
工作條件如下:0~20s機械臂為空載運動,2個俯仰液壓缸各負載機械臂自重m=2000kg一半質量,建模誤差和未建模部分d(x,t)=200sin(t);20s后機械臂負載增加1000kg,由于負載增加會導致d(x,t)隨之增加,d(x,t)=500sin(t)。仿真期間液壓缸在額定速度下伸縮3個周期,x1d=0.1sin(0.4t)。
仿真指令信號如圖4所示。分析圖5,0s~20s期間ARC的跟蹤誤差為-1.3mm~0.3mm,ESOARC的跟蹤誤差為-0.4mm~0.1mm,20s后由于負載突然的增大,ARC的跟蹤誤差突然增大到10mm,通過圖4也可發現20s時ARC軌跡明顯偏離指令信號,相比之下ESOARC仍能很好的跟蹤指令信號,突然的變負載對其影響很小,因此ESOARC魯棒性更加優越。分析圖6,可以看出ESOARC的輸出信號更加平滑,適合于實際系統中應用。圖7驗證了設計的觀測器可以有效對系統中不確定性干擾進行估計。

圖4 指令信號

圖5 跟蹤誤差

圖6 控制信號

圖7 觀測器干擾估計
6 結語
本文針對重載機械臂電液伺服系統的特點,建立了考慮Stribeck摩擦模型的重載機械臂俯仰缸電液伺服系統數學模型,設計了基于擴張觀測器的自適應魯棒控制器。將擴張狀態觀測器和采用反演法設計的自適應魯棒控制器相融合,對系統中存在的不匹配干擾和未知參數進行估計。利用Lyapunov穩定性理論驗證了控制器的穩定性,并在MATLAB仿真中測試了控制器在空載和負載條件下的控制性能。結果表明,和ARC相比,ESOARC具有更好的魯棒性和跟蹤性能,更加適合于重載機械臂上的應用。

