預測控制對串級被控對象結構變化的要求：以串聯CSTR為例

汪 磊 羅雄麟

（中國石油大學（北京）信息科學與工程學院自動化系）

化工過程的被控對象一般為多變量系統，通常以串級控制作為控制方法，但是隨著先進化工工藝的發展，對過程控制的要求日漸提高。 當系統出現有約束、 強耦合以及強非線性等特性時，使用常規控制方法無法滿足要求，因此出現了以模型預測控制（Model Predictive Control，MPC）為代表的先進過程控制（Advanced Process Control，APC），該方法在化工過程控制領域成為重要的研究方向［1～6］。

模型預測控制本質為一種基于數學模型并利用計算機實現的優化控制算法，在每一步控制周期內通過預測模型求解預測時域內的開環最優控制問題，獲得當前控制周期內的最優控制動作，最終通過反饋校正實現閉環優化控制［7～9］。

在工業過程中應用預測控制時，通常由預測控制器接收串級控制最終輸出的預測控制被控變量，利用穩態優化得到最優設定值，并且傳輸至串級主回路作為主回路PID控制器的給定值［10，11］。因此，預測控制的被控對象為包括串級控制回路在內的廣義被控對象，這樣可保證整個串級控制回路處在安全、穩定的控制范圍內［12～14］。

但是另一方面，預測控制的引入也會增加部分附帶的問題： 除了PID控制器的參數對預測控制的控制效果有一定影響，預測控制器的增加也相當于增加了串級回路數量，延長了預測控制系統的響應時間。 因此對于部分復雜控制場景可以通過簡化串級回路， 即減少PID控制器與控制回路以獲得更加高效的控制效果。

綜合以上幾個方面的考慮，筆者在預測控制的架構下，針對多入多出（Multiple Input Multiple Output，MIMO） 串級被控對象重新設計了預測控制系統，分析了常規控制層的串級控制結構進行必要簡化的要求。 由于化工過程控制中的串級控制大部分為溫度-流量串級控制方案， 筆者以串聯連續攪拌反應釜 （Continuous Stirred Tank Reactor，CSTR）為例進行仿真對比，在傳統預測控制系統基礎上，給出了底層只有流量控制器與底層只有溫度控制器兩種控制方案。 將Matlab/Simulink軟件作為仿真工具構建串聯CSTR仿真平臺，進行控制系統的設計與實現，結合實際情況探究此類問題的解決方法。 結果表明，在化工過程中應用先進控制時，宜簡化常規控制層的串級控制結構。

1 串級被控對象在預測控制架構下多層串級存在的問題分析

在預測控制架構下，預測控制的輸出送給常規控制作為給定值，相當于增加常規控制層中串級回路的數量，造成多層串級問題，最終導致常規控制層的組態復雜度增加，響應時間延長。 因此，針對此類復雜度高的問題，如何在傳統預測控制結構的基礎上通過簡化結構降低系統復雜度，值得進一步探究。

在化工過程控制中， 通常由串級控制組成常規控制層， 并且在預測控制架構下作為預測控制被控對象， 串級回路的最終輸出實時反饋回預測控制器［15，16］，控制結構框圖如圖1所 示。預測控制的引入相當于增加底層串級回路的數量，即雙層串級回路變為多層串級回路，對于多入多出串級控制尤為明顯。 并且由于多層串級的存在， 串級控制的主回路由常規情況下的定值控制轉變為預測控制架構下的隨動控制，由主回路轉變為預測控制的副回路， 因此對應的主回路PID控制器參數是否需要整定也需要關注。

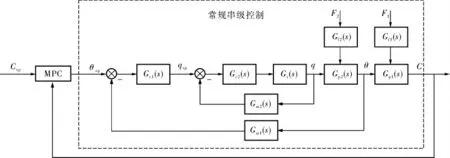
圖1 預測控制架構下的常規串級控制結構框圖

圖1中，q、θ、C分別代表化工工藝裝置內的流量、溫度和濃度參數，qsp、θsp、Csp分別為對應的給定值；Gp1（s）、Gp2（s）分別為被控裝置中主、副被控變量在穩態操作點由線性化得到的傳遞函數；Gm1（s）、Gm2（s）為反饋通道傳遞函數；Gc1（s）、Gc2（s）為主、副控制器傳遞函數；Gv（s）為流量控制回路中流量閥的傳遞函數；Gf1（s）、Gf2（s）為擾動通道傳遞函數，F1、F2分別為進入主、副被控對象的擾動輸入。對于圖1中的常規串級控制來說，無論取消其主回路還是副回路，由于MPC控制器的存在，仍然相當于串級控制。 鑒于以上分析，筆者考慮改變常規串級控制的結構，達到減少串級回路數量的目的。

以化工過程中普遍存在的MIMO串級控制系統為例， 該MIMO控制系統通常由多個單入單出（Single In Single Out，SISO） 串級控制系統通過輸出耦合而成，SISO串級控制結構如圖1虛線框部分所示。 由于在化工過程中，工藝裝置內發生的復雜的化學、 物理反應以及各類擾動均與流量息息相關，所以在該串級控制系統中，副回路通常輸出流量被控變量，實現對工藝裝置內溫度、成分、液位及濃度等主被控變量的輸出控制。

值得注意的是， 雖然在化工過程控制中，可以通過串聯的主、副控制器使工藝裝置作為串級被控對象穩定運行，但是穩態情況下，被控裝置中各變量之間的傳遞函數無從得知。 因此，可以在傳統MIMO串級控制系統架構下， 對主回路設定值θsp增加階躍輸入， 以方便地獲得MIMO串級回路中各變量q、θ、C的階躍響應輸出數據， 進而通過系統辨識的方法獲得輸入輸出傳遞函數矩陣H1（s）、H2（s）、H3（s），消除θsp，即可得到被控裝置內各變量之間的傳遞函數矩陣：

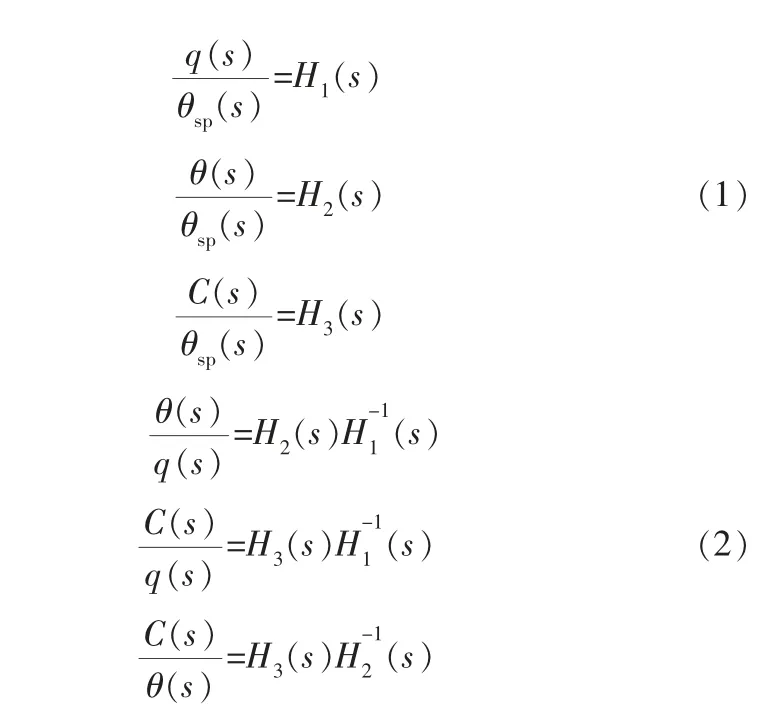
在MIMO控制系統中， 當輸入輸出維數相同時為方系統，不相同時為非方系統。 本研究中的MIMO系統均為方系統，維數為n。 在方系統的傳遞函數矩陣中，主對角線位置的傳遞函數分別表示每一路輸入對應每一路輸出的傳遞函數。 例如在式（2）中的傳遞函數矩陣H2（s）H（s）中，第1個主對角線元素位置的傳遞函數表示第1路串級回路中流量q到溫度θ的傳遞函數Gp2（s）。 因此，根據主對角線位置的傳遞函數，即可忽略變量的輸出耦合，得到每一路SISO串級結構中各被控變量之間的傳遞函數，即圖1中的Gp1（s）、Gp2（s）。因此，可以利用式（2）進一步分析，得出在MIMO串級控制中， 每一路SISO串級控制轉變為如圖2所示SISO單回路控制時的傳遞函數矩陣。

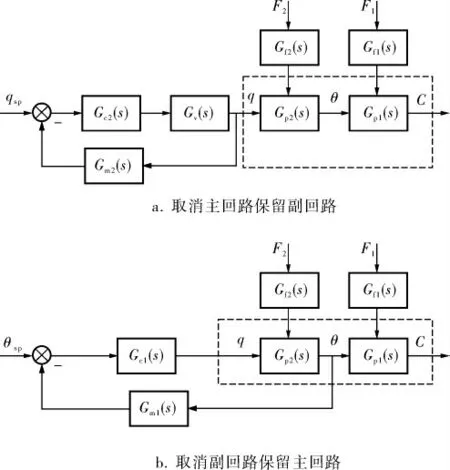
圖2 常規串級控制轉變為單回路控制

常規MIMO串級控制結構未改變時， 其串級主被控變量設定值θsp對被控變量C的傳遞函數矩陣為G0（s），由于G0（s）等價于式（1）中的H3（s），因此，將其植入MPC控制器即可完成傳統預測控制系統的實現。

為了實現MIMO控制系統每一路SISO串級控制按照圖2a所示取消主回路保留副回路時的預測控制系統的設計， 可假設此時MIMO控制系統的傳遞函數矩陣為G1（s）（式（3））。 由于工業現場無法直接取消主回路，對該單回路控制系統進行系統辨識，因此筆者提出隨后的理論推導以獲得該傳遞函數矩陣。 由于圖2a中輸入輸出傳遞函數對應于G1（s）的主對角線元素位置的傳遞函數，因此可以利用式（4），由G0（s）得到G1（s）的主對角線元素位置的傳遞函數，非主對角線元素位置的傳遞函數可以利用輸出相互耦合作用具體分析得知，進而得到取消主回路結構的傳遞函數矩陣G1（s），式（4）中的參數i（i∈N+）表示MIMO串級控制系統中SISO串級回路的序號。將G1（s）植入MPC控制器，即可實現預測控制輸出操縱變量由θsp轉變為流量優化給定值qsp，將其作為副回路的給定值，最終實現此類預測控制系統。

同理，每一路串級控制回路中，按照圖2b所示取消副回路而保留主回路時，上層預測控制輸出操縱變量需要重新轉變為串級主被控變量θ的給定值θsp。 假設此時MIMO控制系統傳遞函數矩陣 為G2（s）（式（3）），同 理 可 以 利 用 式（5）得 到G2（s）主對角線元素的傳遞函數，即圖2b中單回路控制結構的傳遞函數。 式（5）中Gflow（s）為串級副回路的傳遞函數，將Gm1（s）、Gm2（s）設置為1。 同樣利用實際情況中的輸出耦合得到非主對角線元素的傳遞函數，進而得到傳遞函數矩陣G2（s），將G2（s）植入MPC控制器即可實現預測控制輸出操縱變量為溫度優化給定值θsp，將其作為主回路給定值，最終實現預測控制系統。

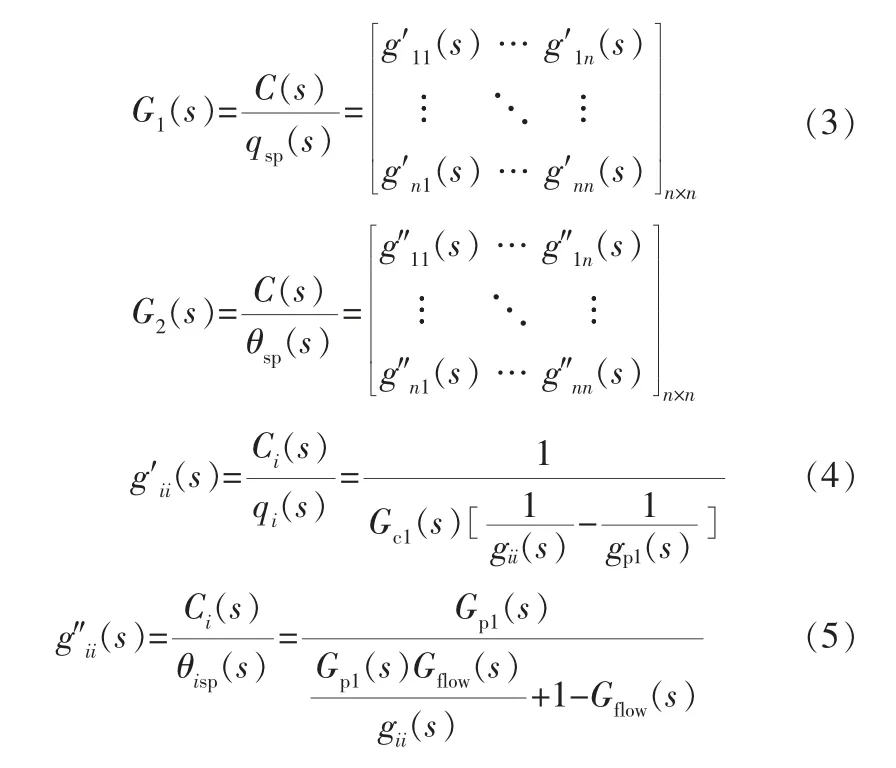
根據以上兩類常規MIMO串級控制系統結構發生改變時的分析可知： 在預測控制架構下，無論對常規串級控制結構做出取消副回路還是主回路的改變，皆可按照式（1）～（5）得到預測控制的參考模型并達到輸出操縱變量改變的要求。

2 串級CSTR仿真平臺的建立

針對第1節的理論分析以及化工領域廣泛存在的“流量被控變量-溫度主被控變量”的串級控制系統［17～19］，筆者以一類化工領域常見的串聯連續攪拌反應釜為被控裝置進行仿真［20］，系統結構原理如圖3所示。

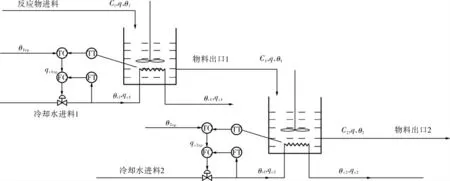
圖3 串聯CSTR控制結構原理

該CSTR被控裝置主要組成為一對串聯反應釜、對應冷卻水管道與反應物進出料管道，主要目的為通過反應釜內的攪拌作用使進料反應物進行放熱反應， 由冷卻水流量qc1、qc2分別通過熱量交換調節釜內溫度θ1、θ2和反應物濃度C1、C2，并且假設兩個反應釜內反應物進料與出料流量q均保持一致，使得兩個反應釜液位不變，處于理想控制狀態。 因此可以在Simulink仿真軟件中，通過串級控制實現對串聯反應釜的控制，構成雙入雙出串級CSTR。

物料與能量衡算公式如下：

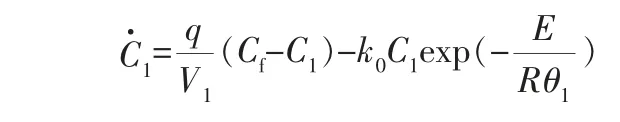
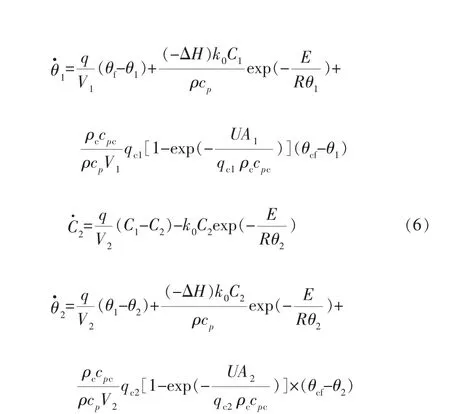
CSTR模型參數見表1。

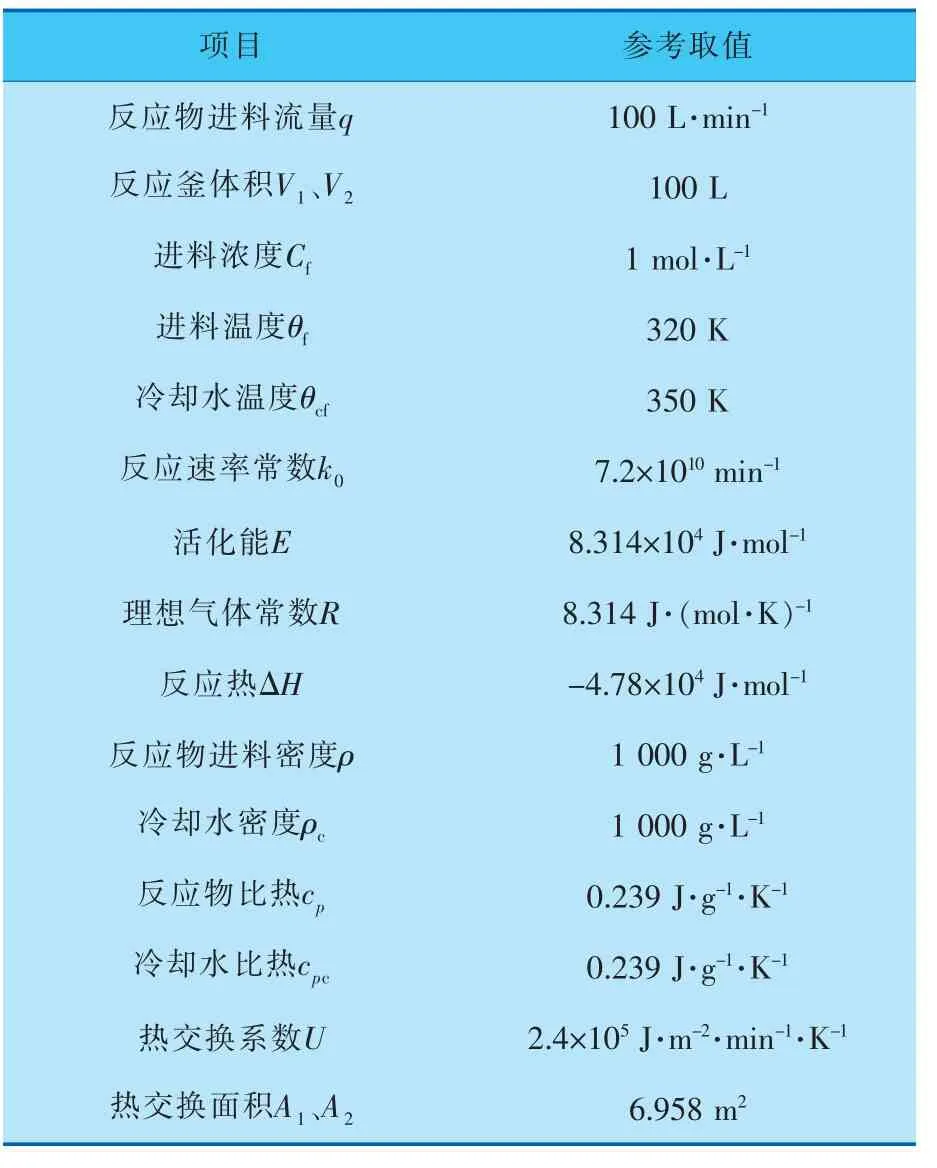
表1 CSTR模型參數

首先通過式（6）和表1中的模型參數，在Simulink軟件中編寫微分方程，搭建非線性串聯CSTR實物模型作為實驗被控裝置。 其次，分別通過串級控制實現對兩個串聯反應釜內冷卻水流量qc1、qc2和物料溫度θ1、θ2的控制，并且串級回路中副回路為流量控制，主回路為溫度控制，均采用常規PID控制器。 最終通過調節PID控制器參數，實現對 該 非 線 性CSTR 在 穩 態 點 ［θ1，C1，θ2，C2］=［448，0.06425，428，0.00659］附近的控制，建立雙入雙出串級CSTR仿真平臺。

在添加MPC控制器前，為了以實例驗證減少串級回路數量的影響，可以分別取消串級CSTR的主、副回路。 改變3種不同控制結構下的流量設定值qcsp與溫度設定值θsp， 分別調節PID控制器參數使最終濃度輸出重新達到0.007 00 mol/L并且穩態時間最短，此時PID參數處于最優，動態響應過程如圖4所示， 以變化幅度的±1%為允許誤差帶，計算得出最終穩態時間ts1=3.5 min、ts2=2.5 min、ts3=1.4 min， 因此可以得出相對于傳統串級控制，減少串級主、副回路可以使得穩態時間分別減少28.5%、60.0%左右。

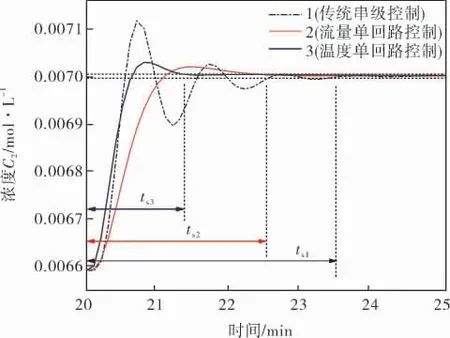
圖4 添加MPC控制器前3種不同控制結構下的動態響應

在添加MPC控制器時，首先以傳統串級控制結構下的串級CSTR作為預測控制被控對象，預測控 制 系 統 結 構 如 圖5 所 示。 在 圖5 中，Gqθ（s）、GθC（s）、G′qθ（s）、G′θC（s）分別表示在穩態情況下第1、2個反應釜內冷卻水流量qc對產品溫度θ、產品溫度θ對反應物濃度C之間的傳遞函數；Gf1（s）、Gf2（s）為第1個反應釜的濃度與溫度輸出對第2個反應釜的干擾作用；G′m1（s）、G′m2（s）、G′c1（s）、G′c2（s）、G′v（s）為第2條串級回路中相應的傳遞函數。

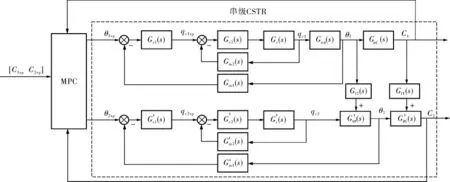
圖5 傳統預測控制架構下的MIMO串級CSTR被控對象

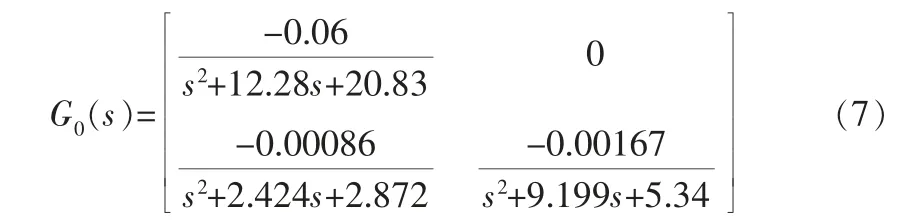
設置MPC 控制器的控制周期t1=ts1/60=0.058 min，保證預測時域長度為ts1/4，因此設置預測步數P=15，控制步數M＝8，仿真得出CSTR裝置最終輸出反應物濃度C2在傳統預測控制架構下的控制效果，結果如圖8曲線1所示。其穩態時間ts1變為5 min，因此可以驗證添加MPC回路使得串級控制回路復雜度增加、響應時間延長。

為了得到減少回路后的串級CSTR的傳遞函數矩陣， 可以在串級控制結構下通過階躍響應測試得到式（1）、（2），將主對角線元素進行傳遞函數降階處理后，最終得到每個反應釜內流量qc、溫度θ與反應物濃度C三者之間的傳遞函數（表2）以及Gf1（s）、Gf2（s）。根據G0（s）和表2內的傳遞函數，可以根據式（3）～（5）對串級被控對象結構進行改變。

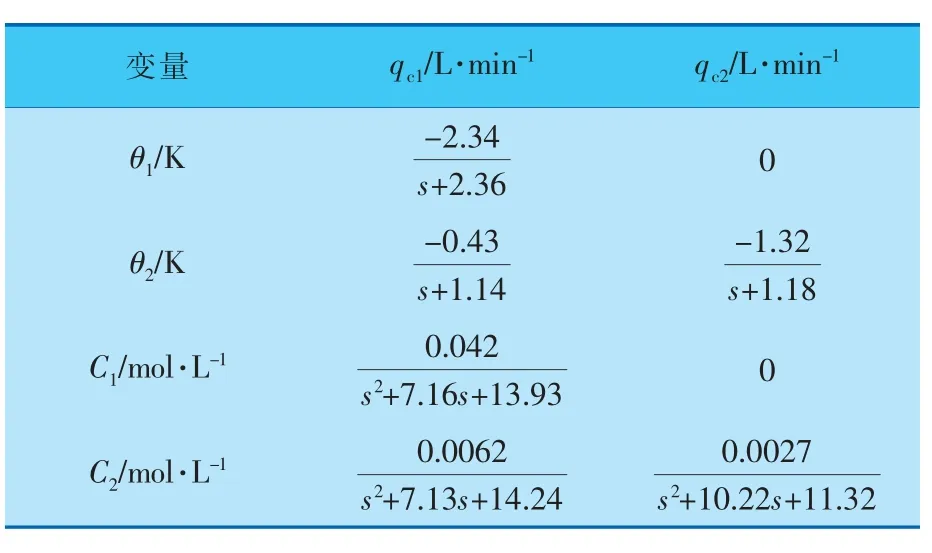
表2 CSTR裝置內變量傳遞函數變量

3 常規控制層只有流量控制器的預測控制設計與實現

傳統預測控制架構下，CSTR裝置中共有流量qc、 溫度θ與濃度C三大類被控變量（Controlled Variable，CV）， 分別納入串級與預測控制反饋回路。 MPC 控制器輸出操縱變量（Manipulated Variable，MV）為溫度優化給定值θsp，將其作為常規控制層中溫度主回路給定值，通過串級回路實現對不同CV的穩態輸出。 但是，由于CV全部納入反饋， 造成常規控制層存在多層串級的問題，導致裝置復雜度增加、 系統響應時間延長等問題。因此根據以上分析，可以減少串級副回路或主回路，以該串聯CSTR裝置為例進行預測控制系統的設計，觀察各類CV的最終控制效果。

筆者首先設計串級控制回路轉變為只有流量PID控制器時的流量單回路控制結構， 預測控制系統結構原理如圖6所示。

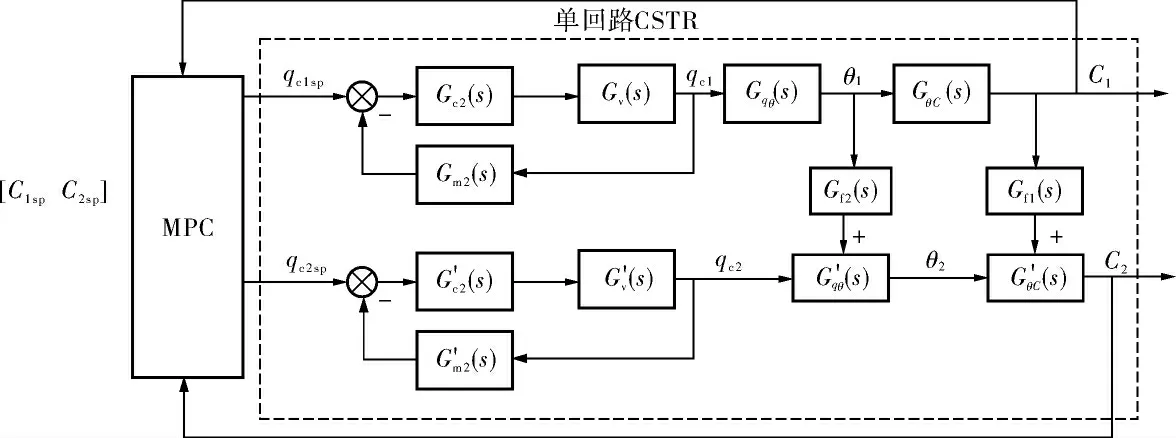
圖6 常規控制層只有流量控制器的預測控制原理

此時，MPC控制器的輸出MV需要轉變為冷卻水流量的給定值qcsp，將其作為流量控制回路的給定值， 實現對CSTR裝置內冷卻水流量的控制，進而控制反應釜內的溫度與濃度。 此控制結構相當于利用MPC控制器取代串級控制結構中的全部溫度PID控制器， 充分利用了預測控制處理多入多出控制系統的先進性，重新構建了由MPC控制器與PID控制器通過串聯組成的串級控制系統，保證了在減少控制回路時系統依然具備串級控制的穩定性。

為實現上述預測控制系統的設計，首先需要對植入MPC控制器的參考模型做出改變，使得預測控制輸出對應MV。 根據以上分析，最終由下式得到傳遞函數矩陣G1（s）：

通過串級CSTR仿真平臺，將G1（s）當作參考模型植入MPC控制器，并且設置MPC控制器的控制周期t2=ts2/60=0.042 min，預測時域為ts2/4，因此取預測步數P=15，控制步數M=7，最終得出MPC控制器輸出MV為流量優化給定值。 由于減少了溫度PID控制器， 此時串級CSTR只保留流量PID控制器，因此在PID參數整定方面更加簡單，并且此時原流量副回路同樣處于副回路位置，起隨動控制作用，因此其PID參數無需調整。

（2）法制建設不健全，法制觀念淡薄。盡管我國針對建筑市場的不正之風制定了一系列法律法規，但對一些違法行為缺乏相應的處罰條款，各方主體法制觀念淡薄，一些單位和個人仍然知法犯法，有些人根本不學法、不守法，我行我素，膽子很大，沒有絲毫規矩和約束，心存僥幸心理，以身試法。

為了觀察此時預測控制系統在穩態點附近的控制效果，筆者在20 min系統達到穩態時改變MPC控制器濃度設定值，使濃度從0.006 59 mol/L重新達到0.007 00 mol/L；在30 min時，添加幅值為2%的反應物進料流量正弦波擾動為預測控制可測擾動，觀察CSTR內反應物濃度C2的動態響應效果，最終結果如圖8中曲線2所示。

4 常規控制層只有溫度控制器的預測控制設計與實現

為了達到減少串級回路數量的目的，同樣可以設計串級回路轉變為只有溫度PID控制器的單回路控制結構。

此時MPC控制器與溫度PID 控制器串聯，CSTR工藝裝置內溫度與濃度兩類CV分別反饋到溫度PID控制器與MPC控制器。 因此在結構上分析，在減少結構復雜度的同時，預測控制系統同樣具有串級控制的穩定性，系統控制結構原理如圖7所示。

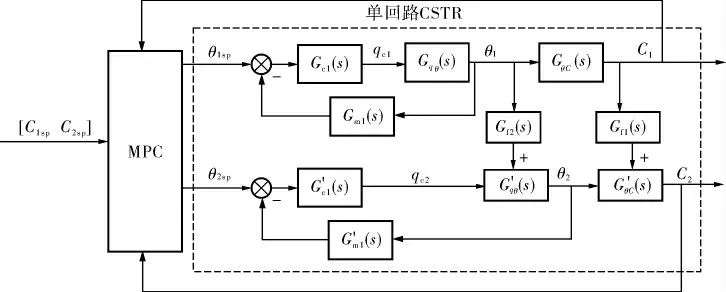
圖7 常規控制層只有溫度控制器的預測控制原理

MPC控制器輸出MV重新轉變為溫度優化給定值θsp，將其作為溫度單回路設定值。溫度PID控制器輸出控制變量直接作用于CSTR裝置內的流量閥，由于流量調節閥可在較短時間內輸出響應， 故在取消流量副回路時，其傳遞函數可忽略不計。

為了在串級CSTR仿真平臺實現該預測控制系統的設計，首先需要得到串級CSTR取消副回路后的傳遞函數矩陣G2（s）。 根據以上分析，最終可由下式得到溫度給定值θsp到濃度輸出C的傳遞函數矩陣G2（s）：

其中，Gflow（s）、G′flow（s）分別為第1、2條串級回路中流量副回路閉環傳遞函數。

在串級CSTR平臺中，將G2（s）作為參考模型植入MPC控制器， 同樣設置MPC控制器的控制周期t3=ts3/60=0.023 min，預測時域為ts3/4，于是取預測步數P=15，控制步數M=8，此時MPC控制器輸出MV重新轉變為溫度優化給定值θsp，并且作為溫度控制回路的給定值， 最終實現對CSTR中各類CV的控制輸出。

由第1節分析可知， 此時溫度回路由串級主回路轉變為預測控制副回路，由定值控制轉變為隨動控制。 因此需要進一步調整溫度PID控制器的參數大小， 即減弱積分作用適當增強比例作用，使溫度回路快速反應。

同樣， 當該預測控制系統在20 min處于穩態時，改變反應物濃度設定值，使濃度從0.006 59 mol/L重新達到0.007 00 mol/L；在30 min時，添加幅值為2%的反應物進料流量正弦波擾動為預測控制可測擾動，最終控制效果如圖8中曲線3所示。

通過綜合分析預測控制架構下，傳統串級控制與取消串級主回路、 副回路情況下的3條不同控制效果曲線，可以得知，相比于傳統情況下的串級控制結構，取消串級中主、副回路可以在預測控制架構下減少系統響應時間。 例如從圖8中可以看出，以傳統串級CSTR作為MPC被控對象時穩態時間ts1=5.0 min，減少串級回路后的流量單回路控制與溫度單回路控制的穩態時間ts2、ts3分別為3.2、3.8 min， 即減少一條串級回路可使得穩態時間分別減少36%、24%左右。 除此之外，在正弦擾動情況下兩種單回路控制可以更快速地消除擾動，因此綜合得出取消溫度主回路效果更佳。

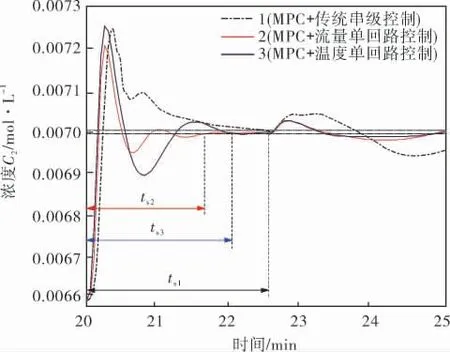
圖8 3種不同控制結構下的動態響應

5 結束語

在預測控制架構下，傳統串級控制具有響應時間延長與組態復雜的問題，因此可以對常規控制層串級結構做出簡化，通過公式給出由串級控制轉變為主變量單回路控制、副變量單回路控制時的預測控制器廣義被控對象模型。 最后通過搭建串級CSTR控制平臺，給出了預測控制系統的具體設計步驟， 以CSTR為實物模型進行了仿真對比。 最終得出串級回路取消溫度主回路時效果最好的結論，這樣不僅可以減少預測控制系統的穩態調節時間，而且達到了降低串級控制組態復雜度的目的。