基于多核支持向量機的多模態過程故障檢測

李 元 李 榕

（沈陽化工大學信息工程學院）

在大數據與人工智能時代背景下，工業自動化得到迅速發展， 工業生產過程也越來越復雜。化工生產過程中，任何一個微小故障都可能引起產品質量變化，造成經濟損失，同時也關乎工廠操作人員的生命安全和企業財產安全， 因此，對復雜工業背景下的故障診斷提出了更高的要求。

為了提高控制系統故障檢測的性能，基于數據驅動的故障診斷方法得到快速發展，并應用于各 種 工 業 過 程［1～3］。 主 元 分 析（Principal Component Analysis，PCA） 作為工業過程故障診斷領域最經典的方法，被廣泛應用于各種工業過程監測中，PCA主要適用于處理相關變量引起的線性問題，并且要求過程數據服從單模態高斯分布的假設，因此在非線性多模態工業過程中無法得到滿意的檢測效果。 核主元分析 （Kernel Principal Component Analysis，KPCA）［4］的提出在一定程度上擴展了PCA的適用范圍， 通過引入核函數將數據映射至高維使其線性可分，然后在高維空間使用主元分析方法，但KPCA仍然存在一系列問題，如算法魯棒性較差、泛化能力不強等，在解決多模態問題方面仍然存在局限性。Zhang X M和Li Y提出基于主多項式分析 （Principal Polynomial Analysis，PPA）的故障檢測方法［5］，利用主多項式分量來描述數據的非線性特征， 但由于使用T2和SPE統計量，在解決多模態過程中檢測受到限制。He Q P 和Wang J 提 出 基 于K 最 近 鄰 算 法（KNearest Neighbor，KNN）的故障檢測方法，然而當處理具有較大方差多模態樣本時，檢測效果并不理想［6］。

Vapnik V N 提出了支持向量機（Support Vector Machines，SVM）［7］，由于SVM在解決工業生產過程中的高維數、非線性等特征上具有顯著優勢，并 且 在 圖 像 識 別［8］、文 本 分 類［9］及 故 障 診斷［10］等眾多領域被廣泛應用，SVM逐漸成為學術界關注的熱點以及機器學習研究的熱門話題。 但是，SVM的性能在很大程度上依賴于所選擇的核函數，而在具體情況下如何選擇最佳的核函數尚無完備的理論依據，如果使用一個不恰當的核函數，就可能產生比在原始空間更差的結果［11］。 針對上述問題，出現了大量有關組合核的研究［12～14］，即多核學習方法［15］，其中常見組合多核方式有直接求和核、 加權求和核及加權多項式擴展核等。文獻［16］采用線性加權求和核作為SVM的核函數， 并將其應用于高光譜影像分類中， 與單核SVM分類器對比發現，多核SVM取得了較高的分類正確率。 文獻［17］將傳統核模糊聚類算法中的單一高斯核函數替換為多個高斯核函數混合，并結合馬爾科夫隨機場的先驗概率，結果表明分割精度明顯優于傳統核模糊聚類算法。

多核SVM相比于單核SVM以其更優的性能在眾多領域受到國內外學者的廣泛關注。 經過多核函數映射后形成的新空間是由多個子空間組合而成的， 新空間能夠組合各子空間的映射能力，從而更好地適應復雜數據。 因此，筆者提出一種基于局部相對概率密度（Local Relative Probability Density，LRPD）的多核支持向量機（Multi-Kernel Support Vector Machine，MKSVM）的故障檢測方法LRPD-MKSVM。將LRPD-MKSVM方法應用于田納西-伊斯曼（Tennessee Eastman，TE）多模態數據集中進行故障檢測。 由于多模態數據具有多中心、變量非高斯性等特點，為了減少數據分布特性對檢測性能的影響， 先用LRPD對多模態數據進行預處理，在此基礎上使用MKSVM分類器對多模態過程進行監測， 并通過TE過程的仿真，驗證LRPD-MKSVM對具有多模態和非線性特征的工業過程進行有效的故障檢測。

1 LRPD-MKSVM算法

1.1 SVM

針對兩分類樣本近似線性分類問題，假設給定樣本訓練集D=｛（x1，y1），（x2，y2），…，（xn，yn）｝，樣本類別yi∈｛-1，1｝，i=1，2，…，n。 SVM分類器思想旨在樣本集空間中找到一個最大分離超平面，將樣本劃分到不同類別，即：

其中，權重向量w=（w1，w2，…，wd），b為位移項。

在分類過程中允許某些點分類錯誤，提高了SVM的容錯率，SVM引入松弛變量ζi和懲罰參數C，建立目標函數：

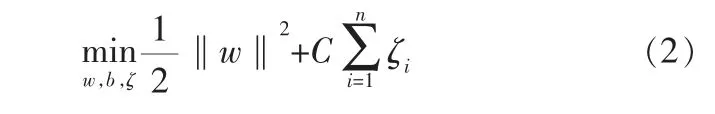
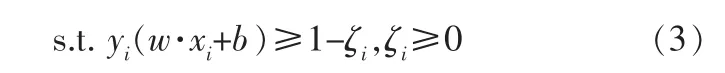
為了求解式（2），利用拉格朗日對偶性將原始問題轉換為對偶問題：

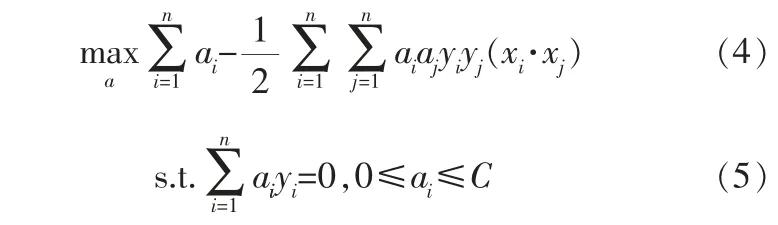
其中，ai為拉格朗日乘子。

當數據集線性不可分時，首先通過非線性映射φ:Rn→H將數據樣本映射至高維空間， 使數據能夠線性劃分，然后再使用線性分類SVM學習方法訓練分類模型。 但往往直接定義映射函數較為困難，而且在計算映射之后的內積運算就更加復雜。 因此，定義核函數K（xi，xj）=φ（xi）·φ（xj），避免了顯式地定義映射函數和在高維特征空間的內積運算，在低維空間進行計算而實際效果表現在高維特征空間，簡化了運算。 將式（4）中的xi·xj內積用核函數代替，則得到核化SVM目標函數：

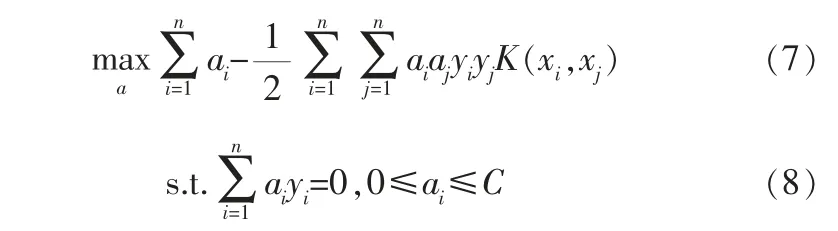
相應的決策函數可以寫為：

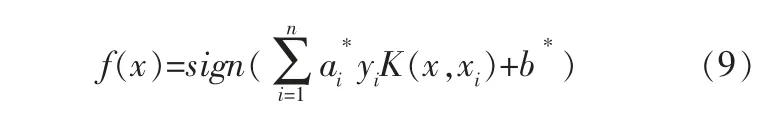
1.2 MKSVM

當涉及到非線性數據分類問題時，巧妙地利用線性分類學習方法與核函數能夠對非線性問題進行有效處理。 通過結合核函數與線性SVM學習機，能夠對非線性數據進行有效分類。 然而在SVM的應用中，當樣本數據量較大、高維特征空間分布不平坦且存在異構信息時，單一選擇局部核函數或全局核函數，并不能滿足數據分類問題的需要。 因此，筆者使用線性加權方式構建多核函數，通過不同核函數的映射，使得數據在新空間得到更好的表達，進而提高分類精度。

設有M個核函數，包含局部和全局核函數，核函數表達式如下：

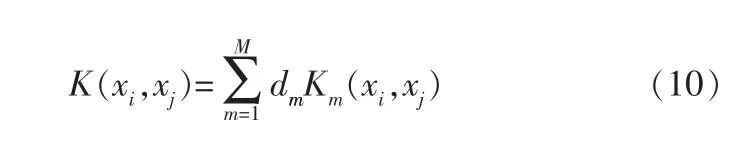
多核SVM求解目標為：

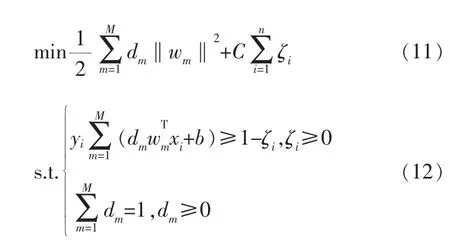
其中，dm為核權重系數，Km為基本核函數，wm為第m個核函數所對應的權重向量。

按照原始SVM問題求解方式，則可轉換為：

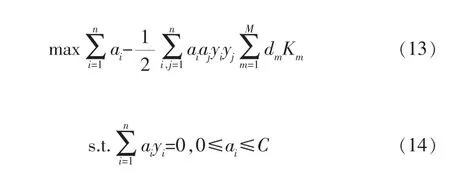
進一步求解最終的決策函數：

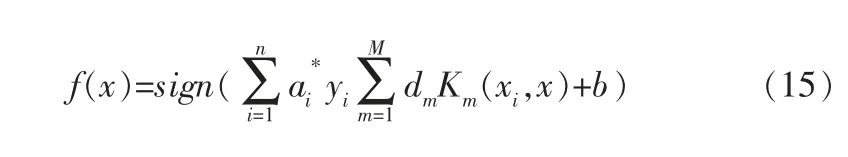
文獻［18～20］表明，局部核函數和全局核函數無法同時兼具學習能力和推廣能力，因此為了充分結合兩者的優點，筆者構造滿足Mercer定理［21］的多核函數，訓練性能更佳的多核SVM分類器，以提高分類精度。

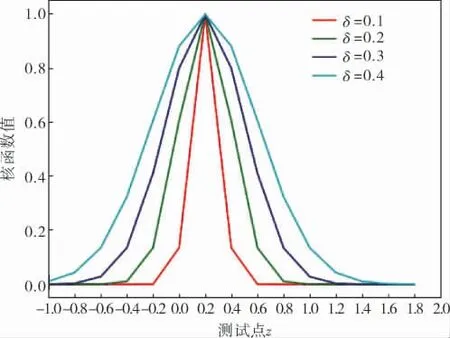
圖1 高斯核函數曲線

多項式核函數K（z，z1）=（z·z1+c）d，取c=1。 令多項式核次數d為1、2、3、4，計算不同次數的多項式對應的核函數在測試點在z1=0.2的核函數值并繪制圖像（圖2）。 由圖2可知，多項式核函數允許距離測試點較遠的數據點對核函數值產生一定影響，適合處理具有全局特征的數據集，即具有較強的推廣能力。

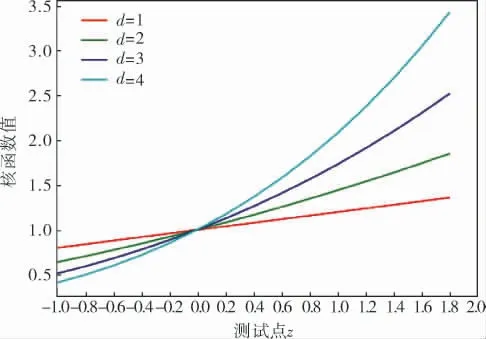
圖2 多項式核函數曲線

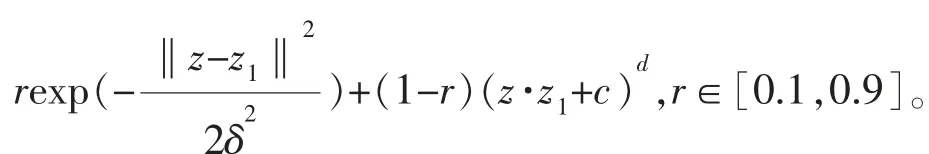
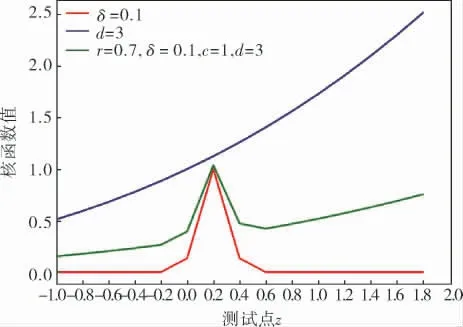
圖3 多核函數曲線

2 基于LRPD-MKSVM的多模態過程故障檢測

如果直接將多核SVM算法應用于多模態過程，其檢測性能并不突出。 為了提高算法對多模態過程的檢測率， 先利用局部概率密度方法［22，23］將多模態數據轉換為單模態數據，然后用MKSVM進行故障檢測。基于LRPD-MKSVM的故障檢測方法分為離線建模和在線檢測兩個步驟，檢測流程如圖4所示。

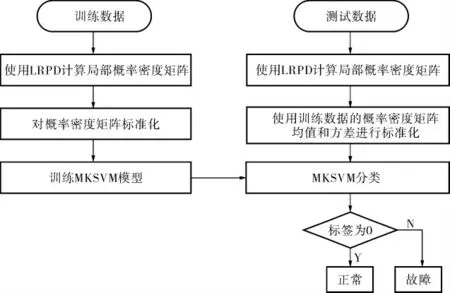
圖4 LRPD-MKSVM方法故障檢測流程

離線建模的操作步驟如下：

a. 獲取正常和故障操作條件下的歷史數據集，記為Xtrain=［x1，x2，…，xm］T∈Rm×n；

b. 用式（15）計算Xtrain的局部概率密度矩陣并進行標準化處理，得到矩陣ain；

其中，步驟b的計算式為：

在線檢測的操作步驟如下：

a. 用式（16）計算測試數據Xtest的局部概率密度矩陣；

b. 運用建模數據的均值和方差對測試數據的局部概率密度矩陣進行標準化，得到數據集；

3 工業仿真實例

本研究的仿真實例數據選用TE數據集［24～27］。TE過程模擬21種預編程故障，多種故障類型能夠清晰真實地反映實際工業過程中存在的問題，詳見表1。

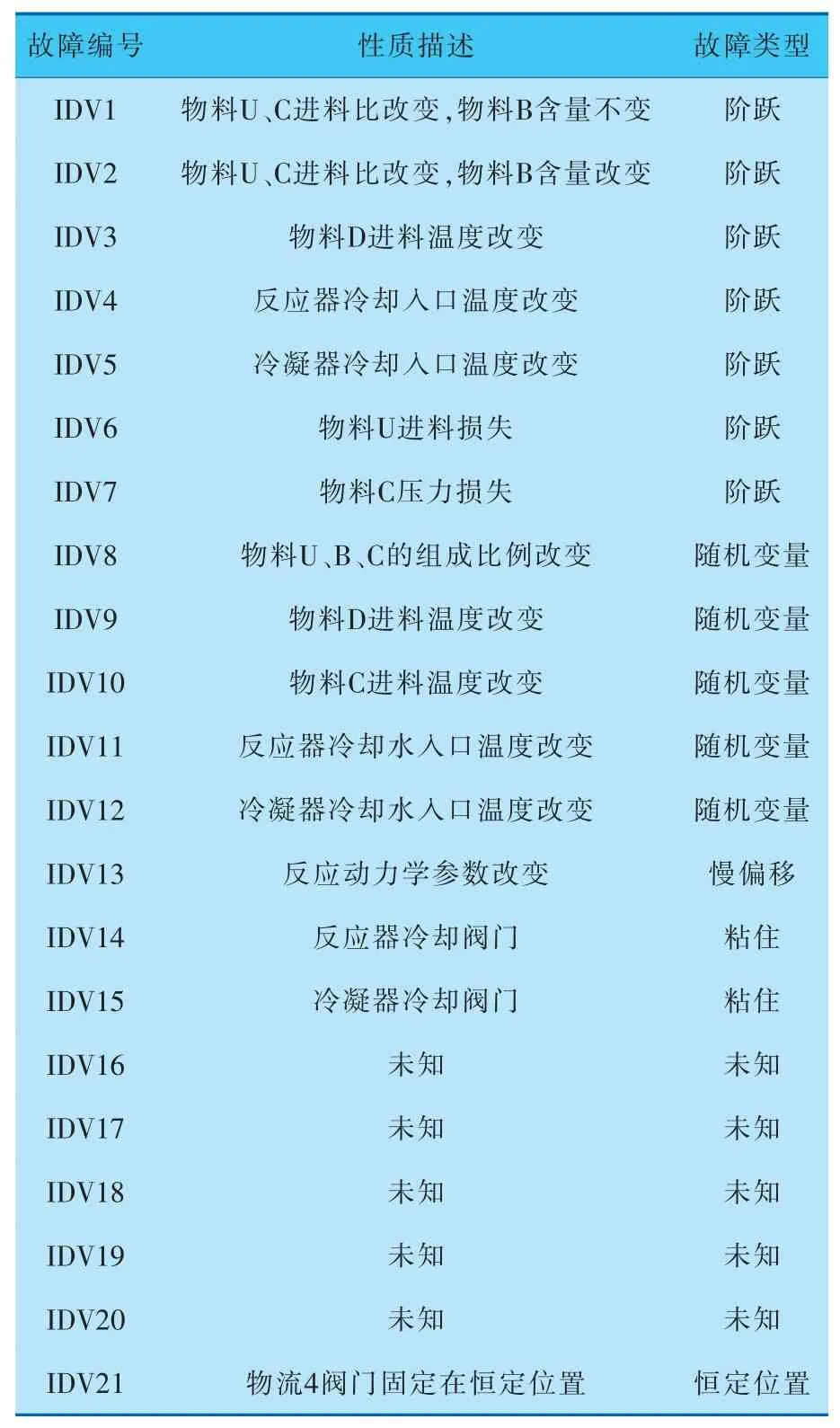
表1 TE過程的21種故障

改變過程中產物G和H的比例， 可以得到TE過程中6種不同的工作模態，詳見表2。

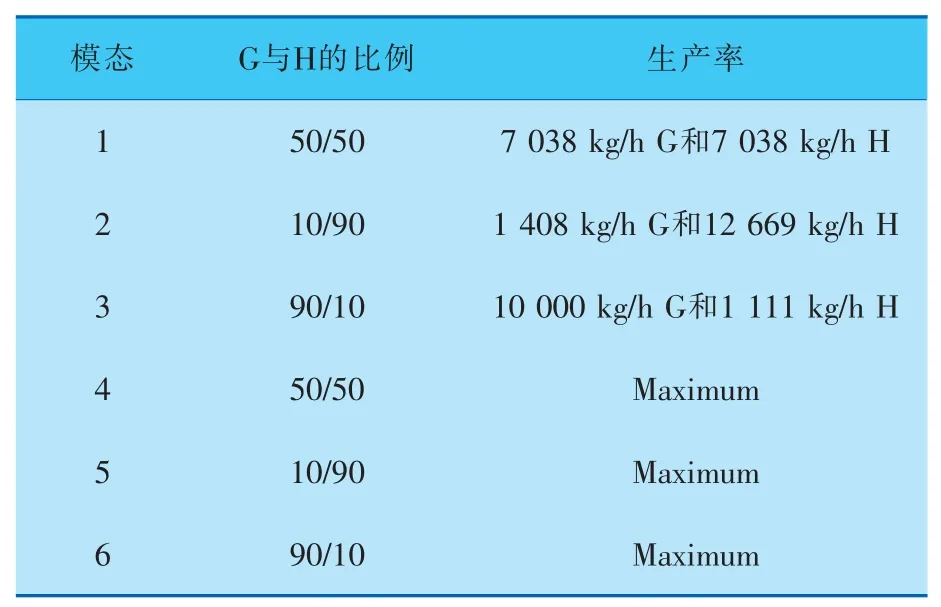
表2 TE過程的工作模態

本次仿真在TE過程的模態1和模態3進行。本例中， 從模態1和模態3分別選取160個正常數據和200個故障數據作為SVM的訓練數據集， 選取模態1和模態3中的故障1、5、7～9、11～13、18和19作為測試故障類型。 測試數據集從模態1和模態3每個故障類型下選取160個正常數據和200個故障數據組成。 將正常樣本數據標簽定義為0，故障樣本數據標簽定義為1。在TE多模態仿真過程中，對TE多模態過程的10個故障運用局部相對概率密度進行預處理， 然后使用RBFSVM、POLYSVM和MKSVM方法分別對測試數據進行分類。

分別采用RBFSVM、POLYSVM和筆者提出的MKSVM方法對TE過程的10種故障進行分類對比。 RBFSVM核函數的最優δ值在［0.01，0.1，1］。POLYSVM核函數的偏移量c和多項式核次數d均在［1，2，3］。 對于MKSVM核函數中的參數構建四維網格搜索尋參， 確定權重系數r設置為0.5，RBFSVM中參數δ設置為0.1，POLYSVM中偏移量c設置為1，多項式核次數d設置為1。 另外，懲罰參數C均設置為1。

表3 匯 總 了 基 于RBFSVM、POLYSVM 和MKSVM對TE過程10種故障的檢測結果，可見，加權組合的多核SVM相比單核SVM， 平均分類正確率有很大程度的提高，對比RBFSVM和POLYSVM分別提高了15.0%和8.9%。

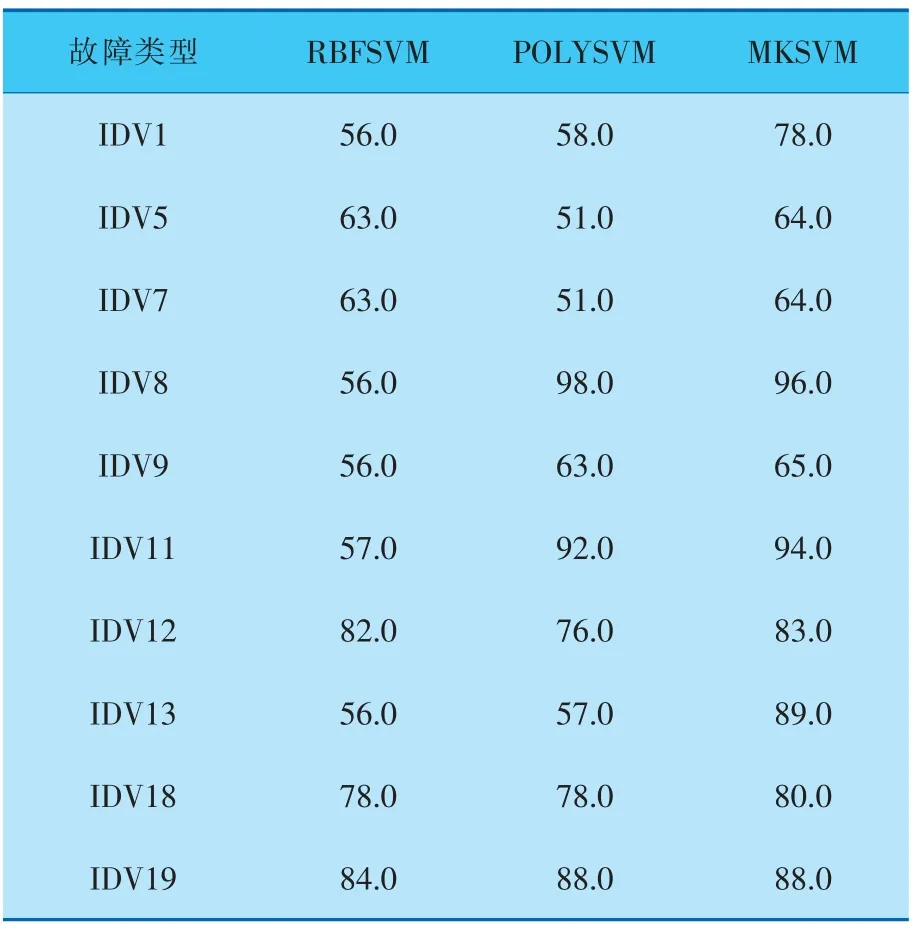
表3 基于3種核函數SVM對TE過程10個故障的分類正確率 %

為了說明基于MKSVM檢測方法的有效性，分別比較了基于RBFSVM、POLYSVM和MKSVM方法對故障1和故障13的檢測結果，結果如圖5、6所示。

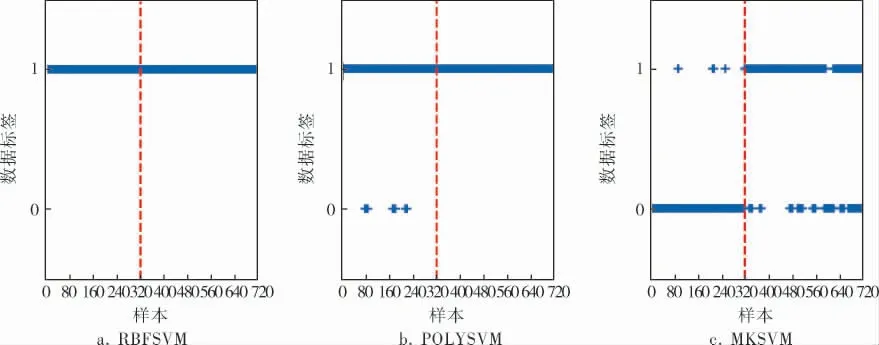
圖6 3種核函數對故障13的檢測結果

在故障1中，物料B含量不變，物料U、C進料比改變，產生了一個階躍性改變故障，擾亂了系統的正常運行。 在此故障中，MKSVM分類的正確率高于RBFSVM和POLYSVM兩種檢測方法，分別提高 了22.0%和20.0%，MKSVM 相 比RBFSVM 和POLYSVM，對于數據分布學習更加高效，提取信息更加全面，所以相比其他兩種檢測方法分類正確率就會更高。 盡管RBFSVM具有較高的故障檢測率， 但對于正常數據并不敏感， 誤報率很高；POLYSVM雖然誤報率為0， 但是對于故障數據不能有效學習， 故障檢測率低于MKSVM方法。 而MKSVM檢測方法在誤報率為0的情況下， 相比其他兩種核函數，分類正確率最高，具有更好的檢測性能。

故障13是由反應動力學參數改變而引起的慢偏移故障，RBFSVM和POLYSVM對于故障數據都能有效識別，具有非常好的檢測效果，但對于正常數據不能有效檢測。 而在MKSVM多核函數映射的背景下，由子空間構成的組合空間可以發揮各個基本核的不同特征映射能力，對于異構數據的不同特征分量分別使用相應的核函數進行處理， 使得數據能夠在高維空間得到更為精確、合理的表達， 提高樣本的分類正確率， 因此MKSVM相比RBFSVM和MKSVM， 分類正確率能夠達到89.0%，取得更為滿意的檢測結果。

4 結束語

針對工業過程中數據具有的多模態、非線性特征，提出基于局部相對概率密度的多核支持向量機工業過程故障檢測方法，引入局部概率函數將多模態數據轉換為單模態數據，消除多模態數據分布特性對故障檢測性能的影響，在此基礎上使用不同核函數SVM進行故障檢測。 將所提出的方法應用于TE多模態工業過程中， 應用結果表明， 筆者提出的MKSVM方法的分類正確率優于RBFSVM與POLYSVM方法的，能大幅提高故障檢測的準確性，在實際生產中有重要的指導意義。