基于泰勒展開的柔性加減速控制算法研究

王佳煒 崔 平 宮子陽 黃澤耀 范啟富

（上海交通大學電子信息與電氣工程學院自動化系 系統控制與信息處理教育部重點實驗室）

數控技術是現代設備制造業的支柱性技術，推進數控技術的研發，對高端制造業的發展具有重要的作用，決定了制造裝備的高階性能。 高速和高精度是當前數控機床追求的兩大衡量數控產品性能的重要技術指標，目前進給率最大的數控機床可以在240 m/min的條件下對復雜型面進行精確加工； 加工最高精度已經達到納米級別。機床運動時的加減速控制是影響這兩項指標的關鍵技術之一，直接決定了機床的生產效率和加工面質量［1］。

加減速控制算法的種類可以根據其加速度曲線的形狀進行劃分，直線型加減速控制算法的特性是算法計算量最小、加減速最猛烈、效率最高，因此，最先被廣泛采用，但是算法在加減速階段存在加速度突變現象， 容易導致數控機床振動，因此，僅適用于精度要求不高的加工場合［2］。為緩解加速度突變帶來的振動，數控行業內陸續提出了三角型、梯型及S型等加減速控制算法，算法的加工柔性和計算復雜度與其加速度曲線的連續性正相關，較直線型加減速控制算法，能限制機床產生的部分沖擊，但因未考慮加加速度曲線的連續性，在高速高精度的加工場景下，加工工件的表面光潔度不高，不適用于對加工面質量要求高的場合［3，4］。

為解決加減速控制算法其加加速度不連續導致的問題，張相勝等構造了加加速度曲線呈三角形變化的模型［5］，由于模型的加加速度曲線僅C1連續， 因此不能為機床的柔性帶來很大的提升。 高偉強等采用3次多項式函數確保加加速度曲線連續［6］，但加加速度曲線不對稱，在加減速過程的起末位置存在沖擊。 李金良等對構造的連續速度曲線逐次積分［7］，僅得到線性變化的加加速度曲線，系統柔性不高。

為解決上述問題， 筆者基于S型加減速控制算法，提出了一種加加速度連續的加減速控制策略，構造了連續的加加速度曲線；根據相鄰加工路徑間的夾角，動態調整加工路徑的最大加加速度值，同時滿足拐角處的降速要求；根據當前加工段長度在加工總長度的占比，對微小線段上的加減速過程進行平滑處理。 通過仿真驗證整套基于S型加速減控制策略的控制性能， 證實該策略能有效減輕加工中數控機床的振動，提高加工柔性和加工效率。

1 加加速度連續方程的推導

為得到連續的加加速度曲線，直接取正弦曲線作為加加速度曲線， 正弦函數加加速度方程為：

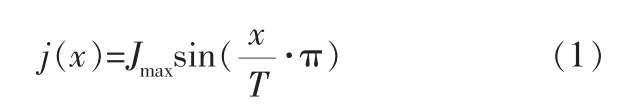
其中，T為單個變加速階段時間，函數在T/2處取得最大加加速度Jmax。 但正弦函數計算復雜，在算力有限的場合無法滿足系統實時計算的要求。為兼顧正弦加減速的柔性和算力要求，選取低次多項式對正弦函數進行逼近，構造更適用的加加速度曲線。

考慮到計算復雜度，取sin x的二階泰勒多項式為逼近多項式。 對正弦函數在x=π/2處進行二階泰勒展開，為滿足單個變加速階段的起終點加加速度為零， 即在x≥0的區間內至少有兩個零點，對展開后的多項式進行移位并歸一化，得到的函數曲線如圖1所示。

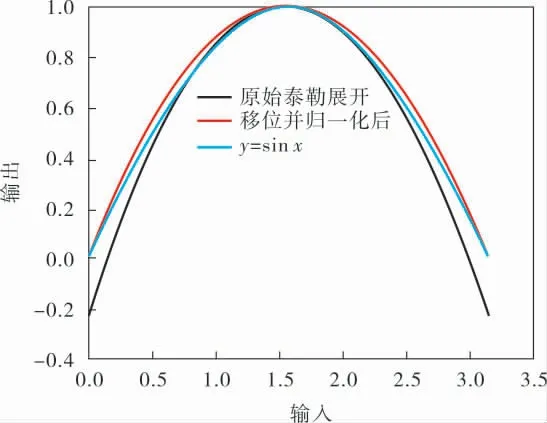
圖1 正弦函數及其二階泰勒展開多項式函數曲線

如圖1所示， 處理后的多項式與sin x有較高的近似度，取其作為加加速度曲線，即：

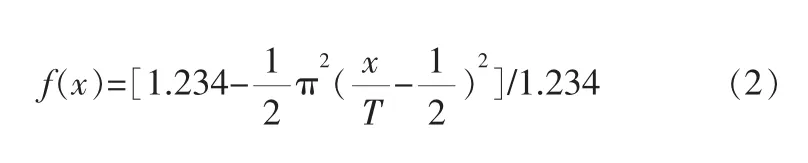
為確保單個變加速階段的起終點加加速度為零，即x=T和x=0時，f（x）=0，對系數進行取整，得到二階的逼近多項式：

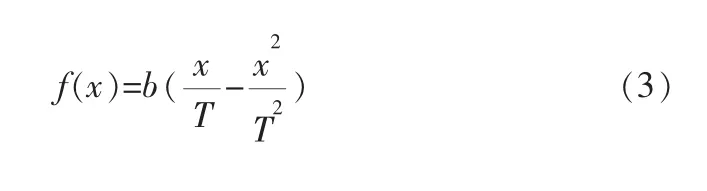
其中，b為待定系數，滿足在區間［0，T］內f（x）≤Jmax，且在x=T/2處取得最大值Jmax，解得｜b｜=4Jmax。

最終得到加加速度方程如下：

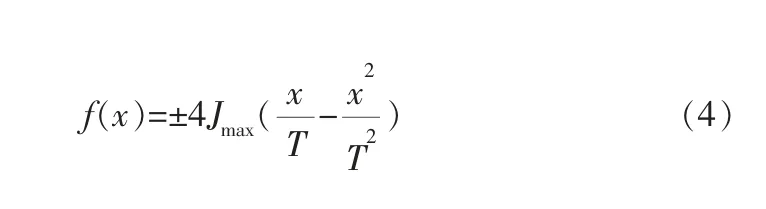
該加加速度方程具有C2連續且相比正弦函數計算更簡單，相比傳統方法由四次多項式構造速度曲線反推加加速度曲線的方法系數更少，計算速度更快［8，9］。

2 柔性加減速控制算法構建策略

首先由加加速度方程推導得到整個加減速控制算法，其次為滿足相鄰加工路徑夾角處的降速要求，根據夾角的大小，動態調整每段加工路徑的最大加加速度值，最后為減少不必要的加減速過程引起的機床受力變化，根據當前加工段長度在加工總長度的占比，平滑微小線段上的加減速過程。

2.1 加加速度連續的加減速算法

五段式加減速控制算法其速度曲線一般由加加速、減加速、勻速、減減速和加減速5個階段構成，根據加工路徑的長度和機床運動學參數限制，可能由于無法加速至最大速度而丟失勻速階段，只存在4個變加速階段。

由加加速度、加速度、速度和位移之間的關系，有：

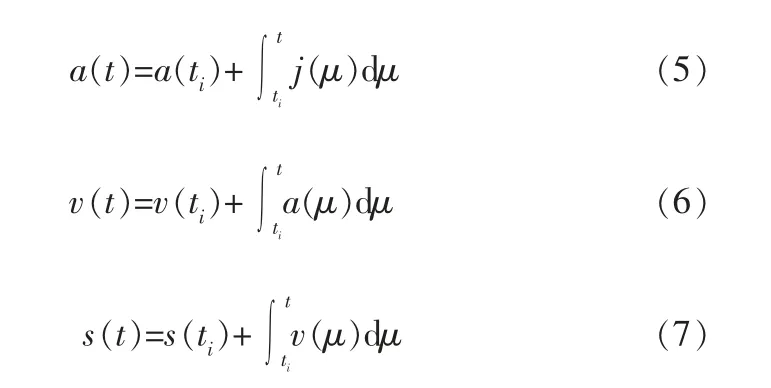
其中，a為加速度，v為速度，s為位移，ti為起始時間，μ為運動學參數方程的自變量。

與五段S型加減速控制類似， 本研究中加加速度方程j（t）如下：

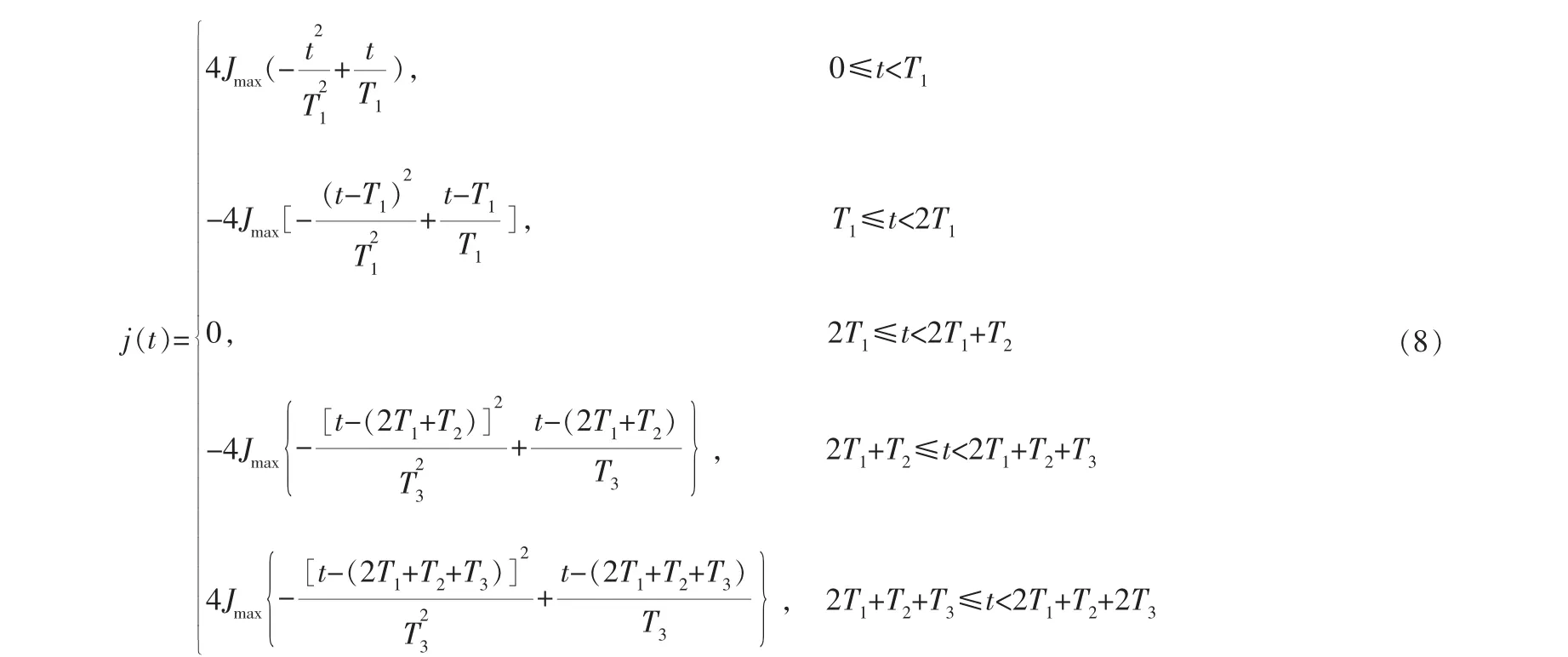
其中，T1、T2、T3分別表示一段加工路徑上的加加速段時長、勻速段時長、減減速段時長。

由式（5）～（8）推出加速度、速度、位移的計算公式分別為：

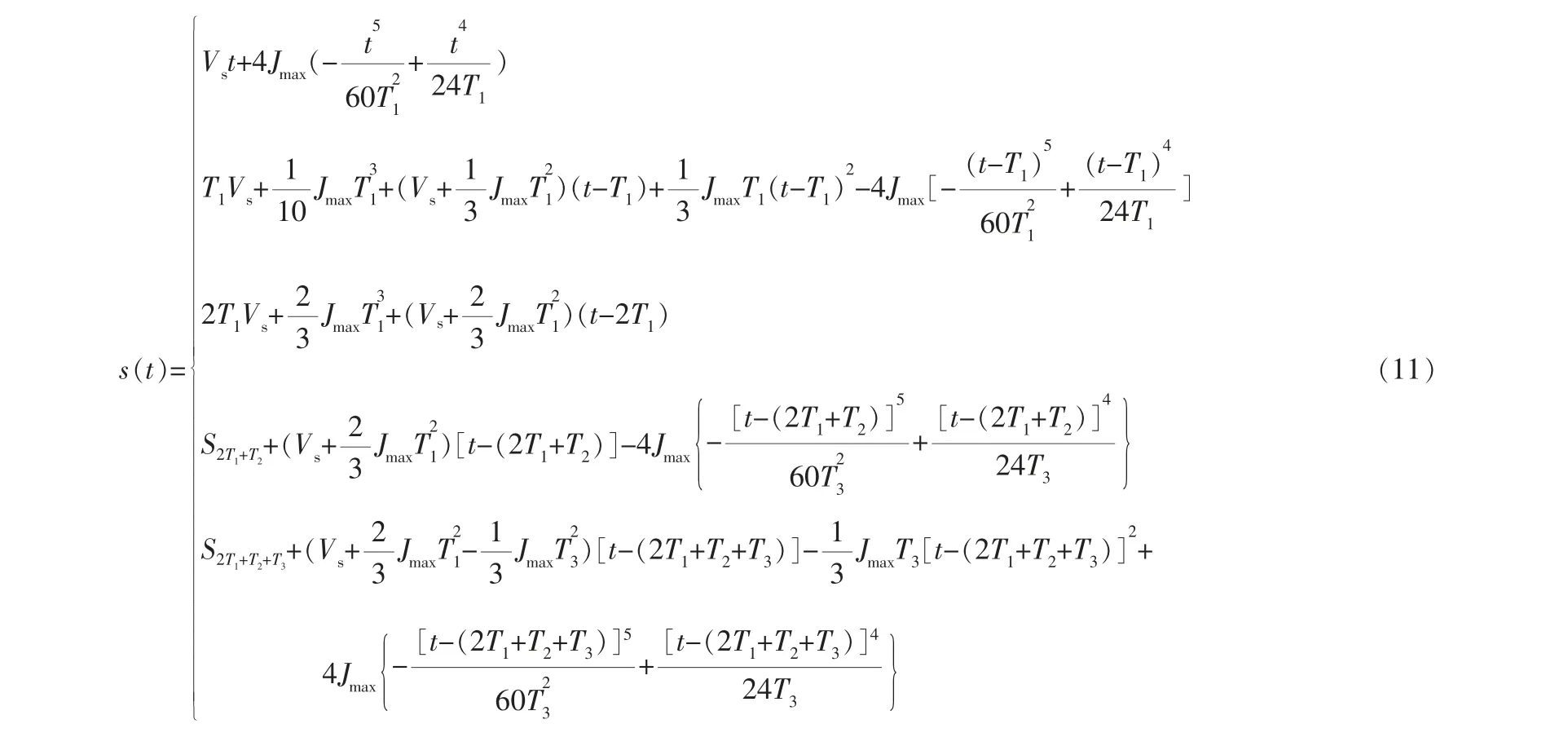
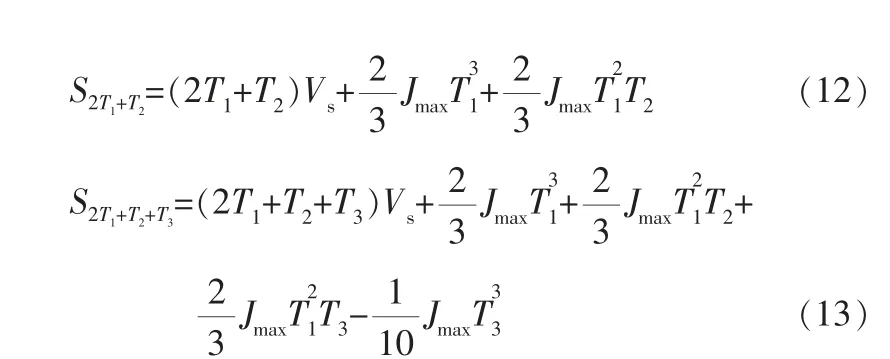
其中，Vs為初始速度。 式（9）～（11）的取值區間與式（8）相同。

2.2 動態調整加加速度最大值

傳統的加減速控制算法， 其加加速度曲線是階躍的且整個加工過程中最大加加速度值是固定的。最大加加速度決定系統加減速的柔性，若取值超出機床極限，則會產生一定沖擊；取值較小，則運動的加減速過程時間延長，影響加工效率［10］。

與傳統算法相比，筆者構造的加加速度連續加減速算法，由于其加加速度不是瞬間達到最大值，因此加減速過程時間更長。 為提高算法的效率，考慮在進行速度規劃時，根據兩段加工路徑之間的夾角動態改變每一段加工路徑的加加速度最大值［11，12］。

當兩段加工路徑之間的夾角較小時，由速度方向變化產生的機床沖擊比較輕微，因此允許以較高的速度進行加工。 當夾角過大時，必須快速將速度降低以保證平穩換向，因此需要更大的加加速度以縮短減速時間，滿足高速、穩定的加工要求。

唐艷麗等總結了過渡速度與夾角的關系［13］，即夾角趨近于0°時，允許的過渡速度非線性地迅速增大，因此筆者將一段加工路徑上加加速度最大值與其相鄰路徑間夾角的關系確立為：

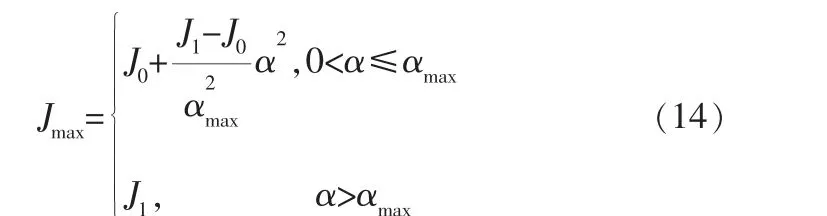
其中，α為相鄰路徑間的夾角；夾角最大值αmax的設定取決于系統所能承受的最大加加速度限制；J0、J1分別為系統允許的最小與最大加加速度。

單段路徑上加加速度最大值與相鄰路徑間夾角的關系如圖2所示。

當前路徑上加加速度的最大值與相鄰路徑間夾角正相關， αmax、J0、J1根據不同的機床機械性能、加工刀路、加工工藝在進行速度規劃時設定合適的值。

2.3 短線段加減速平滑

在高速、高精度的加工過程中，若加工路徑出現連續微小線段，由于加工路徑較短，初始速度Vs與末尾速度Ve值近似， 若均小于這段路徑上系統允許的最大加工速度Vmax， 傳統的加減速控制方法在微小線段上存在加速后立即減速的加減速過程，而這種連續頻繁的加減速，不可避免地會對機床造成沖擊，導致加工質量下降，但對于加工效率的提升很微弱，因此考慮對這類微小線段上的加減速過程進行限制。 筆者提出一種基于加工段長度的加減速平滑策略。

若S0<λS，則：

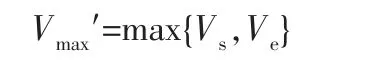
其中，S0表示當前路徑長度；S表示加工路徑的總長度；λ表示允許存在加減速過程的最小加工路徑長度占加工路徑總長度的比例；Vmax′表示當前路徑上的最大速度。

對加工段上的最大速度進行限制，能保證微小線段上只存在加速或者減速過程，避免機床所受的力頻繁換向，能有效減小對機床的沖擊。

3 仿真示例

為驗證筆者構造的加加速度曲線的連續性以及對于微小線段上加減速過程平滑的有效性，取任意8段路徑，起點為（0，5），分別經過（20，5）、（35，5）、 （50，19）、 （54，19）、 （57，16）、 （61，16）、（64，19）到達終點（84，19）。 仿真軌跡如圖3所示。

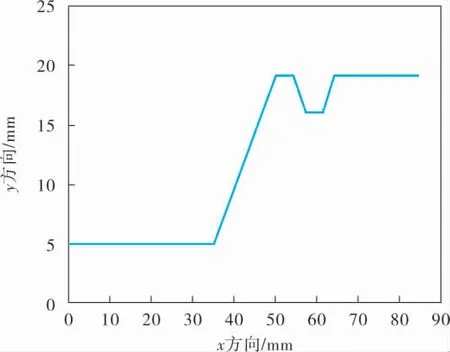
圖3 仿真軌跡

運動學限制參數如下：

各段路徑上的起終點速度見表1。

表1 各段路徑上的起終點速度 mm/s

在插補周期為6 ms時， 通過Matlab得到整個加工路徑上的仿真運動曲線如圖4所示， 藍線代表普通五段式S型加減速控制模型， 綠線代表筆者所提的加加速度連續的柔性加減速控制模型。

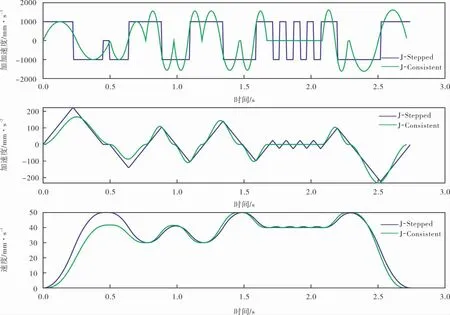
圖4 加減速控制曲線

圖4速度圖上時間［0.00，1.25］區間顯示第1段和第2段路徑上的速度變化， 由于兩段間夾角為零，因此加加速度最大值較低，無法在單段上達到最大速度，而加工時間短于傳統算法，驗證了2.3節中所述的可平滑部分機床運動加減速過程。 其次由圖4加加速度圖可以看出筆者提出的算法中加加速度曲線有良好的連續性，加減速過程更快速，平滑了在時間［1.6，2.1］區間上短線段的加減速過程，算法時間更短，速度曲線、加速度曲線更連續，證明本方法能在實現系統柔性控制的同時，提高整體的加工效率，避免小線段上頻繁加減速的過程。

4 結束語

針對正弦加減速控制算法計算量大的問題，通過對正弦函數進行多項式擬合，得到了一定區間內對稱且連續的加加速度方程，通過依次積分得到五段式新型加減速算法，然后根據相鄰加工段之間的夾角對加工路徑上的加加速度最大值進行調整，并提出微小線段上平滑加減速過程的策略。 仿真結果表明，與傳統的五段式S型加減速算法相比，筆者提出的算法能同時滿足高速與柔性方面的要求，提高加工效率和加工質量。