基于多元智能的數學校本選修課程“四步”實施

【摘 要】 數學校本選修課程作為國家課程的拓展與補充，沒有高考壓力，在課程實施過程中內部動機起著更為主導的作用，學生的多元優勢智能得到更大程度的發揮.以《數學多棱鏡》第四章中“探秘經典”單元—課時教學為例，通過“努力觸發燃點線”“精心打造共同體”“細致滋養生長點”“繽紛絢爛展示群”的“四步”課程實施，讓學生對“基本不等式”與“柯西不等式”的悠久歷史、相互關聯、幾何背景、代數詮釋、思想啟示進行深入探究，在此過程中學生的多元優勢智能助推數理邏輯智能，推動學生的數學探究活動.

【關鍵詞】 校本選修;多元智能;“四步”實施;探秘經典

1 問題緣起

數學校本選修課程作為國家課程的拓展與補充，其實施過程是以國家課程的實施為基本藍圖，但是又較之國家課程有學生更為廣闊的發揮發展空間，因為數學校本選修課程的實施更為自由靈活機動.國家課程以高考影響下的成績目標為導向，對于學生來講有很強的外部動機，而校本選修課程沒有高考的壓力，學生的表現更隨心而動，內部動機起著更為主導的作用.在課程實施過程中，學生潛藏的多元智能得到更大程度的開發，用學生各種優勢智能助推數理邏輯智能，引導學生用數學的眼光觀察世界，用數學的思維思考世界，用數學的語言描述世界.

2 多元智能理論基礎

霍華德加德納認為人的智能是一個復雜的綜合體，涵蓋語言智能、空間視覺智能、運動智能、音樂智能、數理邏輯智能、人際關系智能、自我認知智能、自然觀察者（博物學家）智能、存在智能.就智能的發展問題，加德納認為各種智能的發展存在不同的規律，但從整體而言主要有以下幾點：（1）對于某一個人來說，智能的發展是不平衡的.即每個人都有各自的智能強項和弱項.智能之間的不同組合表現出個體間的智能差異，即每個人都有自己的智能輪廓;（2）智能的發展受教育和文化環境的影響很大.通過教育培養可以提高人的智能，即人的多元智能發展水平的高低關鍵在于后天的開發;（3）不同智能顯現出來的年齡存在明顯差異，應有意識捕捉不同智能發展的最佳時機;（4）不同智能之間存在相互影響，如“瓶頸效應”“補償效應”“催化效應”.

3 《數學多棱鏡》的“四步”課程實施

筆者基于多元智能理論開發的校本選修課程命名為《數學多棱鏡》，之所以命名為《數學多棱鏡》，是因為筆者將課程分為“數海覓蹤，學無止境，多思古今，棱角分明，鏡像萬千”五部分，每部分的課程各具特色.“數海覓蹤”側重對國家課程里的內容二次挖掘;“學無止境”側重學生的奇思妙想;“多思古今”側重從數學史的角度探究高中數學中的某些內容;“棱角分明”側重對經典公式定理的來龍去脈進行探究;“鏡像萬千”側重數學與實際生活的緊密聯系.綜合基于多元智能的校本選修課程實施可以分為“四步”：點燃、構建、深潛、共享.下面筆者以第四章中“探秘經典”的單元—課時教學為例，談談數學校本選修課程的“四步”實施.

3.1 點燃：努力觸發燃點線

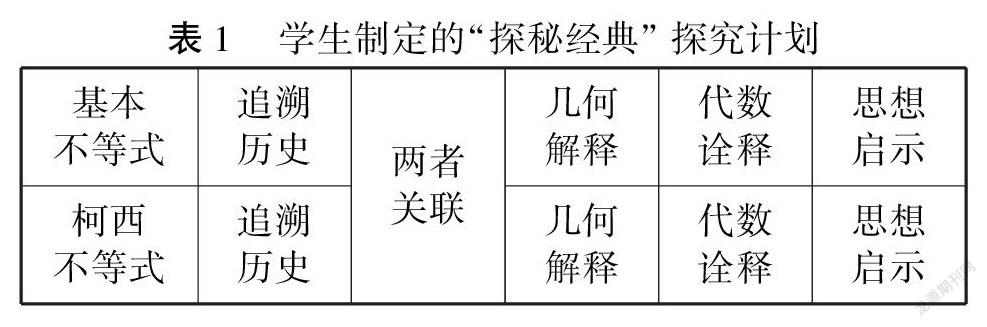
在一般的數學學習中，學生的數學學習往往是被教師提出的問題或任務驅動，而筆者追求的校本選修課程在實施過程中，希望由學生自主自發地發現問題.提出一個問題往往比解決一個問題更重要，因為解決問題也許僅是一個技能而已，而提出新的問題、新的可能性或者從新的角度去看舊的問題，卻需要有創造性的想象力，而且標志著科學的真正進步.在“探秘經典”課程實施的起始階段，筆者意圖讓學生自己尋找感興趣并且想探究的問題.數學中有很多經典的公式、定理、不等式與性質等，所謂的“經典”，可以從不同角度詮釋，學生心目中的“經典”有他們自己的詮釋.教師設計問卷調查學生心目中的“經典”，統計結果表明學生對“經典不等式”感興趣，因此筆者就將“經典”定位在不等式的研究上.進而筆者讓學生選擇心目的“經典不等式”，很多學生都選擇“基本不等式”和“柯西不等式”，于是讓學生自己制定研究計劃，點燃探究火花，觸發思維燃點線.學生通過討論達成共識，制定了以下的研究計劃，盡可能全面揭示“基本不等式”與“柯西不等式”的經典之處.

學生對于制定這樣的探究計劃給出了自己的理由：首先這兩個不等式之所以經典因其具有深厚的歷史底蘊，其次它們的經典之處表現為“經典”與“經典”之間往往存在千絲萬縷的聯系，再次它們的經典之處應該體現為具有非常好的“數形結合”屬性，最后它們的經典之處在于蘊含在其中的思想方法具有推廣價值與意義.燃點線的觸發與研究計劃的制定是一個調動學生自我認知智能與人際關系智能的過程，當然數理邏輯智能依然占據主導地位，而其他智能對數理邏輯智能的輔助與助推作用也顯得尤為關鍵.3.2 構建：精心打造共同體

從高考的角度看，數學需要獨立思考，因此在國家課程的實施過程中，教師更多地是鼓勵學生對問題進行獨立思考和自主探究.但從辯證角度看，事物總有兩方面，如果片面地強調獨立思考，容易閉門造車或出現“當局者迷”的情況，從某種程度上限制了學生多元智能發展的空間.作為國家課程補充的校本選修課程沒有高考壓力，可以充分發揮數學學習共同體的強大功能.精心打造的學習共同體要體現“同組異質”.從智能角度講就是同組的學生盡量擁有不同的優勢智能，這樣的學習共同體具有兩種基本功能：（1）社會強化：建立學習共同體是滿足學習者的自尊和歸屬感需要的重要途徑，這里的自尊與歸屬感也體現在智能的自尊與歸屬感;（2）信息交流：學習者與輔導者進行交流，同時又與同伴進行交流和合作，共同建構知識、分享知識、智能互補.

在“探秘經典”實施過程中，學習共同體內部均進行了不同程度的分工，綜合起來基本都是按照學生的智能優勢進行分工.擁有語言優勢智能的學生側重挖掘與查詢歷史淵源，擁有自然觀察者優勢智能的學生側重研究兩者的關聯，擁有空間視覺智能優勢的學生側重研究幾何解釋，擁有數理邏輯優勢智能的學生側重研究代數詮釋，擁有自我認知優勢智能的學生側重研究思想啟示，而擁有人際關系優勢智能的學生負責綜合各類研究，與眾人磨合，形成展示成果，最終進行匯報的人員可以是擁有數理邏輯優勢智能與語言優勢智能的“組合”.

3.3 深潛：細致滋養生長點

針對學生制定的研究計劃和共同體分工，筆者為學生的研究活動滋養幾個生長點，讓學生的數學思維、素養伴隨著多元智能經歷頓悟、破土而出.3.3.1 經典之“中西方數學發展的比較”

中西方數學文化有著各具特色的發展歷史與特征，我國古代數學擁有璀璨的文化，值得學生去追溯，比較中西方關于兩個經典不等式的研究特色與區別.

（1）基本不等式西方對于基本不等式的研究比較早，公元前6世紀，畢達哥拉斯學派已經知道算術中項、幾何中項以及調和中項，畢氏學派的哲學家阿契塔在《論音樂》中定義了上述三類中項，并把幾何中項小于等于算術中項叫做基本不等式.歐幾里得在《幾何原本》中給出了兩條已知線段之間的幾何中項的作圖方法，如圖1所示，以AB為直徑作半圓ADB，則CD即為AC和CB之間的幾何中項.歐幾里得之后，芝諾多魯斯在《論等周圖形》中給出命題：在邊數相同、周長相等的所有多邊形中，等邊且等角的多邊形的面積最大.在四邊形中便可以得到基本不等式.

我國對于基本不等式的研究最經典的首推“趙爽弦圖”（如圖2所示），趙爽是公元3世紀三國時期東吳的數學家，趙爽弦圖的經典之處在于他用截、割、拼、補來證明代數式之間的恒等關系勾股定理，而“基本不等式”也蘊含于趙爽弦圖中，趙爽在給《周髀算經》作注時寫道：“以圖考之，倍弦實，滿外大方，而多黃實，即勾股差實.以差實減之，開其余，得外大方.大方之面，即勾股并也.”由此可以讓學生探究得到基本不等式.

（2）柯西不等式

也許學生會認為“柯西不等式”顧名思義是由柯西首次提出的，但是如果引導學生再細細查找蛛絲馬跡，便可發現兩個值得斟酌的問題.其一，從歷史角度講，柯西不等式應該稱為“柯西-布尼亞克夫斯基-施瓦茨不等式”，其原因值得學生追溯;其二，從我國歷史角度講，趙爽弦圖的變形圖（比如將趙爽弦圖中的正方形換成平行四邊形等）中也可以得到柯西不等式.

我國古代數學的風格是以形證數，數量關系與空間形式往往是形影不離地并肩發展著，十七世紀笛卡爾解析幾何的發展正是我國這種傳統思想和方法在幾百年停頓后的重現和繼續.不妨可以對學生進行“立德樹人”的愛國主義教育：我國文化傳承于儒家中庸之道，一向比較低調含蓄，而且由于年代久遠，我國的很多數學研究成果未必能夠完整保存下來，所以有待于我們繼續去考證與發現我國古代璀璨的數學文化寶庫.

3.3.2 經典之“兩者間關聯程度的摸索”

數學的發展告訴我們，不同的數學知識之間存在千絲萬縷的聯系，也正是這種聯系推動數學不斷的發展，學生相信“基本不等式”與“柯西不等式”兩大經典不等式之間也存在必然的聯系.學生發現，對于二維柯西不等式（a2+b2）（c2+d2）≥（ac+bd）2，如果取c=d=1時，二維柯西不等式就是二維基本不等式a2+b2≥2ab;而對于三維柯西不等式（a21+a22+a23）（b21+b22+b23）≥（a1b1+a2b2+a3b3）2，如果取b1=b2=b3=1，三維柯西不等式就是基本不等式的變形a21+a22+a23≥a1a2+a2a3+a3a1;如果繼續將柯西不等式推廣到n維，依然可以找到與基本不等式之間的關聯.

數學之間的關聯不僅僅體現在兩個經典不等式橫向之間，也體現在兩個經典不等式與不同知識內容之間.兩個經典不等式原本屬于代數領域研究的內容，但是它們與其他代數領域的內容、幾何領域的內容都存在關聯，因此就有了以下兩個“經典”：幾何背景與代數觀點.3.3.3 經典之“多角度幾何背景的探究”

基本不等式與柯西不等式具有豐富的幾何背景，單從我國古代數學看，兩個不等式都可以與優美幾何圖形緊密相連.隨著幾何學的深入學習，學生知道向量、復數都有幾何詮釋，還有完美體現數形結合的解析幾何，因此兩個經典不等式與向量、復數、解析幾何都有深刻的關聯.比如圖3所示，設平面直角坐標系中兩點A（a1，a2），B（b1，b2），則a=OA=（a1，a2），b=OB=（b1，b2），OD是O到直線BD的垂線段，OB是O到直線BD的斜線段，二維柯西不等式的一種幾何背景是：定點O到直線BD的垂線段OD比斜線段OB更短＼[1＼].3.3.4 經典之“統一性代數觀點的整合”

從代數觀點看兩個經典不等式也可以是多角度的整合，可以從不等式作差的角度、復數集內的三角不等式角度、方程的角度、函數的角度，而不等式、方程、函數三者之間又存在重要關聯，這也是高中數學著重要研究和考查的內容之一，顯示出數學內部的和諧美與統一美.比如基本不等式與對勾函數的緊密聯系，而柯西不等式與某一個一元二次方程的判別式存在關聯，而且可以推廣到n維柯西不等式，從代數觀點，柯西不等式源于平方式非負的性質，這與幾何中距離非負相對應.3.3.5 經典之“合理化思想方法的推廣”

既然兩個經典不等式有著如此悠久的歷史，有著如此默契的關聯，有著如此豐富的幾何背景，有著如此深刻的代數詮釋，那么我們不僅能夠運用這兩個經典不等式解決很多的問題，而且能夠將蘊含其中的思想方法在解決問題上進行推廣應用，比如構造平面圖形解決問題，構造空間圖形解決問題，構造解析幾何圖形解決問題，構造函數解決問題，構造復數解決問題，構造向量解決問題等.3.4 共享：繽紛絢爛展示群

展示是校本選修課程實施的一個重要環節，經過學習共同體對兩個經典不等式的“深潛”，均有所斬獲，通過學習共同體的書面匯報，筆者發現，由于不同的學習共同體的主導優勢智能有所不同，因此探究側重點也會有所不同，探究的深淺程度也有所不同.筆者根據不同學習共同體的優勢與特點幫助他們選擇合適的展示點，由此形成繽紛絢爛的展示群.

通過展示，學生的多元智能得到可視化的體現，讓共同體內的每一位學生的自我價值都得到體現;通過展示，學習共同體內部遺留的問題可以得到不同視角的釋疑，讓學習共同體走出固步自封的象牙塔，產生豁然開朗的頓悟;通過展示，會閃耀出教師意想不到的亮點，讓學生們驚嘆于“原來如此”，折服于同伴的智慧，充分印證了學生驚人的想象力與敏銳的觀察力;通過展示，匯聚成學生的過程作品集，這是學生多元智能相互推動的成果，記錄團隊精誠合作的歷程，形成學生深度學習的智慧結晶.

參考文獻

[1] 李尚志.柯西不等式之幾何白話版＼[J＼].高中數學教與學，2021（07）：41-43.

作者簡介 俞昕（1977—），女，浙江湖州人，正高級教師，碩士;主要研究數學文化、數學校本課程、多元智能等;有多篇論文發表.