從黑盒子到因果律：尋找量子物理的信息原理

陳怡穎，王子竹

(電子科技大學基礎與前沿研究院 成都 611731)

量子理論作為現代物理的兩大基石之一，為物理研究提供了全新的表達方法。然而，量子系統作為一個基于四大基本假設提出的數學空間，其數學符號和動力學方程并不能體現出自然的物理原理。眾所周知，狹義相對論可以從“慣性參考系的等價性”和“光速不變”兩大公理中完整推導出來，因此，眾多物理學家試圖尋找隱藏在量子理論的數學描述中的物理原理。

1935 年 ， Albert Einstein、 Boris Podolsky、Nathan Rosen 三位物理學家提出了第一個物理原理[1]：定域實在論(local realism)，并對量子力學的哥本哈根詮釋提出質疑：量子力學對物理實在的描述是完備的嗎？文章建立在定域實在論的假設之下，規定在某區域發生的事件以不超過光速的傳遞方式影響其他區域，且認為在系統不受任何干擾的情況下，如果可以準確地預測某物理量的值，那么該物理量具有實在性。文章表明，若定域實在論成立，則可以推導出量子力學不完備。這就是量子力學史上著名的“EPR 佯謬”。

然而，“EPR 佯謬”并沒有提出一個好的辦法能夠檢驗量子力學是否提取出與定域實在論有關的物理原理，將兩者進行公平地比較。這導致物理界對“EPR 佯謬”的可靠性爭論不休。一方面，Niels Bohr 作為哥本哈根學派的創始人之一對“EPR 佯謬”提出異議[2]。他認為量子力學中的物理量與測量情景密切相關，這使得“EPR 佯謬”物理實在性在量子物理中的定義本質上模糊不清，其結論并不可靠。另一方面，David Bohm 認為存在一個沒法觀察到，但又存在的確定性物理機制阻礙了量子力學的完備性。1952 年，Bohm 提出量子力學的隱變量因果解釋[3-4]，試圖從量子力學的概率特征中找到一種潛在的不可訪問的機制原理，能夠驗證“EPR 佯謬”。雖然Bohm 的隱變量不滿足定域性，但其觀點促進了一系列關于隱變量理論的物理原理研究。

1964 年，John Bell 首次提出將定域實在論中的物理概念提取出來，用一個不依賴于特定理論形式的數學模型表示[5]。文章將量子力學和定域實在論放入其中進行平等地比較，證明量子力學不能用局部隱藏變量理論(local hidden variable theory, LHVT)解釋。Bell 的理論框架采用黑盒思想(black-box principle)，將實驗室描述成具有有限輸入、輸出集的黑盒子。Bell 根據定域實在論做出假設，分離的黑盒之間不存在超光速通信。因此，所有輸入輸出之間的關聯性都來源于黑盒之間共享的資源。如圖1，以兩體系統為例，Alice 和Bob 的輸入值分別為 {x,y} ， 輸出值分別為 {a,b}。因此，局域隱藏變量模型可以理解為Alice 和Bob 之間共享一種不可測量的資源λ，或者說具有共同的策略λ。

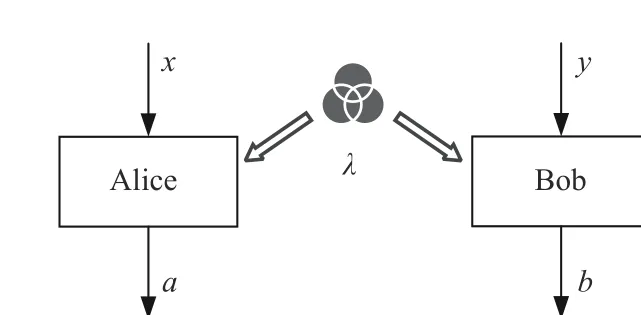
圖1 兩體局域隱藏變量模型

種種研究和實驗結果表明量子態可以是一種非定域資源，以某些量子態為資源的信息傳輸似乎能夠以超光速行進。隨著量子力學中量子糾纏這一概念慢慢被人們熟知，物理學家們開始分析非定域和糾纏的關系。事實上，兩個概念并不是等價的，不是所有的糾纏態都可以破壞Bell 不等式，非定域性是比糾纏更強的量子特性[12]。Bell 非定域性與同時期進行的量子互文性的研究構成了對物理實在性理解的兩大沖擊[13]。量子互文性來自于Andrew Gleason 對希爾伯特空間的封閉子空間上的測度研究[14]。Gleason 證明了所有這樣的測度都可以用量子物理的測量基本假設構造出來：測量結果的概率為測量算符與被測量的密度矩陣乘積的跡。Kochen-Specker(KS)定理表明Gleason 的上述定理直接決定了某些滿足物理實在性要求的測量結果并不是確定性的，而是和這些測量算符與另外哪些測量算符放在一起測量有關[15]。通過對Bell 定理和KS 定理的研究，可以得出結論：物理實在性并不像“EPR 佯謬”所描述的那么經典[16-18]。

可以看出，Bell 定理啟發了物理界對定域性、物理實在性等一系列物理概念的深入理解，對量子基礎研究的貢獻功不可沒。Bell 的模型框架作為定域實在論的抽象表示，為后續物理學家們從量子力學中總結出物理原理提供良好工具。概率和概率關聯性是任何物理理論都可以實現的物理量，是一種基本的數學語言。因此，局域隱變量模型可以看作是一種與某個具體的理論無關的物理原理表示。這一思想又被稱為器件無關原理(device-independent principle)，這樣一種脫離物理實驗器件限制的統一模型可以用于公平地比較量子理論與其他可能的理論，更好地了解量子理論的顯著特征。這是一個剝離物理概念的過程，讓其盡可能地擺脫其物理載體的限制，凝練出具有普適意義的物理原理。這樣的一個過程在其他領域也有類似的例子。在計算領域，人們將算術從算盤或計算器等物理載體中抽離出來，把算術規律抽象成不拘泥于器件形式的算法用以開展研究。器件無關原理貫徹整個“重構量子理論”基礎研究，是一種重要的思考方式。

1992 年，在Bell 模型的基礎上，“無信令”原理作為相對論因果律在量子力學中的對應原理，從量子理論中抽象出來[19]。相對論因果律在物理系統中被描述為“子系統之間的信息傳輸速度不得超過光速”，文獻[19]將該物理概念凝練為量子理論的“無信令”原理(no-signaling principle)。如圖2 所示，其本質上描述的是任何子系統的測量和其他子系統測量結果之間的獨立性。該模型和Bell 局域隱變量模型類似，可以將“無信令”原理投射到與某個特定物理理論無關的廣義模型中使用。準確地說，“無信令”模型又稱為PR box，可以看作是Bell 局域隱變量模型進一步放寬對子系統間關聯的限制，黑盒之間不再共享資源。

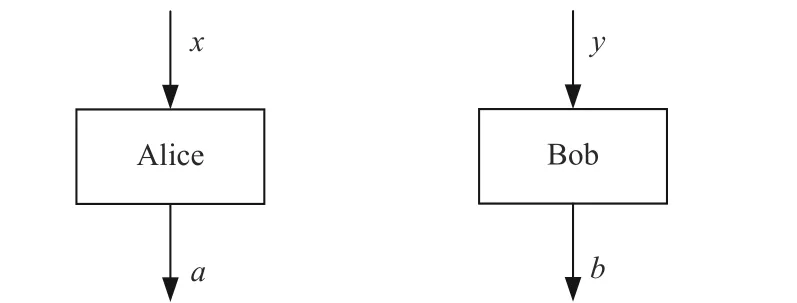
圖2 兩體“無信令”模型圖

一時之間，如何找到準確刻畫量子理論的物理原理成為了諸多物理學家關注的熱點。為達到重構量子力學的最終目的，不僅要從實際應用的物理理論中剝離可靠的物理原理，還需要通過一些操作性語言推導已知的物理原理，復原理論結構，以確保物理原理是量子理論的充分必要條件[20-22]。這樣一種推導物理原理以重構物理理論的過程類似于計算領域中通過用編程語言操縱數據，實現抽象的算法的過程。諸多物理學家紛紛嘗試在此領域深耕，以期探尋其中的奧秘[23-25]。

廣義概率論(generalized probability theories, GPT)便是物理學家們提出的第一種“編程語言”[26-27]。廣義概率論作為一個用于實現物理原理的操作性框架，不受特定理論的限制，延續和推廣了Bell 模型的基本思路。該理論以黑盒為研究單位，帶有限輸入、輸出集的黑盒之間可以通過并行或串行的方式組合成復合系統，并在此基礎上考慮物理系統的狀態、演化和測量[28]。該框架中的所有理論，包括經典理論和量子理論，都具有兩個基本的共性：1) 子系統之間遵循“無信令”原則；2) 復合系統的狀態可以由定域測量結果之間的關聯性決定。

這樣一個脫離量子物理形式的統一操作語言試圖利用提取的簡單物理原理作為條件，推理出一系列思想理論。通過附加或者放寬某些物理原理的限制實現對理論的調整，使其最終等價于量子理論。其中最具代表性的理論為廣義無信號理論[29](generalized nonsignaling theory, GNST)，又稱為盒世界理論[30](box world)。這一理論僅由“無信令”公理刻畫，是非定域性最強的理論，量子理論中被認為特殊的性質在該理論中變得非常普遍。研究盒世界理論對于了解量子理論的特性，探究量子理論的理論構造有著十分重要的意義。

隨著量子信息理論的新興和發展，越來越多的人開始注意到量子計算具有明顯的優勢，理論的非定域性在信息處理上能夠提升通信協議[31-34]。2007年，文獻[29]試圖從信息處理的角度建立GPT 的操作語言，研究物理理論的信息計算特點，為量子理論的研究提供了新的思路。包括在GPT 操作框架下深入研究盒世界的物理性質[30]，以及從量子計算等方面研究量子電路和盒世界電路的計算能力[35-37]。研究發現，盡管盒世界擁有更強的量子非定域關聯，其幾何對偶的測量空間卻有相對定域的性質，不存在類似量子隱形傳輸(quantum teleportation)、量子稠密編碼(quantum dense coding)等非定域的測量性質。

此外，與GPT 操作框架中根據物理原理重建理論不同，不少物理學家延續了“無信令”原理的思想，僅用某些物理原理約束即可推導量子理論的概率相關性，無需進一步將理論細化。如：信息因果原理[38-39](information causality)，宏觀定域原理[39-40](macroscopic locality)和定域正交原理[41-42](local orthogonality)，但這些原理都不能將量子關聯性和其他非定域關聯性完全區分開來。目前為止，最為貼近量子物理特征的理論描述是“Almost quantum”的理論[43]。

另一方面，既然相對論因果律作為唯一刻畫量子理論的物理原理是遠遠不夠的，一些物理學家試圖從反向推理。相對論因果律確定了概率模型中各個黑盒子之間的因果順序，且物理原理的普適性要求黑盒內部的運行機制不拘泥于某一理論形式；相反，若指定概率模型中每個黑盒子內部遵循某一特定理論，允許黑盒之間的因果順序存在不同方式的組合，只要求其滿足該理論的基本數學描述，所有黑盒子之間的概率關聯性滿足現有的因果律嗎？答案是否定的。

2012 年，全局因果結構在量子物理中受到新框架模型的挑戰[44]：當不再對全局因果順序做出假設，規定個體實驗室內部產生輸出的過程服從量子力學時，該物理系統的粒子關聯性將如何描述？該框架模型建立在器件無關思想下，通過研究黑盒的輸入輸出信息剖析其中的全局因果結構。為更好地描述各個黑盒與系統整體的信息，文章利用Choi-Jamio?kowsky 同 構 (Choi-Jamio?kowsky isomorphism)構造高維的量子超映射M(quantum supermap)[45]和過程矩陣W(process matrix)。量子超映射作為將量子操作映射到量子操作的高階變換，體現了物理系統內部的全部操作信息，而過程矩陣作為系統外部信息的高階映射，表示物理系統的整體因果結構。文章通過物理系統的量子超映射M及過程矩陣W，將判斷物理系統是否具有全局因果結構的標準從“物理系統是否打破因果不等式”簡化為“過程矩陣是否可寫成單信道系統過程矩陣的凸組合形式”，最終得出結論：在子系統遵循量子力學但不考慮各個子系統之間因果順序的前提下，物理系統可能出現違背因果不等式的關聯性。這種奇特的因果順序是否真的違背了量子理論？物理學家們并不能找到確鑿的證據肯定地回答這個問題：量子理論或許比我們先前的理解更加匪夷所思。

文獻[44]的思想啟發了人們對因果結構的研究，開始展開一系列在此基礎上的針對經典理論的分析。當物理系統局限于經典概率理論中時，三體及以上的多體系統也會出現未預定義的因果關聯(correlations without predefined causal order)[46]。不僅如此，過程矩陣W在經典系統中存在等價表征，在幾何上可以表示為不確定因果結構組成的凸多胞體，用于優化因果博弈問題[47]。針對經典系統的系統研究進一步發展和豐富了物理理論中因果結構的研究。

隨著量子計算的發展，量子電路開始走進人們的視野，其中量子電路中對操作順序的控制是真正實現廣義量子電路的關鍵[48]。電路控制作為量子電路中因果結構最直接的體現，引發物理學家們展開一系列研究。2021 年，針對操作控制的量子電路系統理論在具有不同控制的電路中分類討論了量子超映射[49]。其中包括利用經典態控制因果順序的經典開關[50](classical switch)，以及利用量子態控制因果順序的量子開關(quantum switch)[50]等。此外，一系列相關研究進一步闡明了不確定的因果順序在量子信息處理中具有一定優勢[51-72]。

多年來，物理學家們不斷地嘗試從實際應用的量子力學中抽象出所有物理原理，并利用這些物理原理重新推導量子理論的邏輯結構。各方圍繞“重構量子理論”這一深刻的基礎問題展開了諸多討論，試圖找到理解量子理論的關鍵線索。為梳理研究脈絡及未來研究方向，本文首先引入研究通過物理原理刻畫真實與假想物理理論關聯性強度的重要工具——廣義概率論，以及其中的典型非定域理論——盒世界理論。隨后，介紹一系列嘗試用于唯一定義量子關聯性的器件無關原理。最后，文章介紹量子物理研究中的另一奇特現象——不確定的因果結構，及其在量子電路中的應用。

1 廣義概率論(generalized probability theories, GPT)

1.1 基本性質

廣義概率論是不拘泥于特定物理理論的一般操作框架，通過推導從物理概念中抽離出來的物理原理構造某一假想理論，從而驗證物理原理和物理理論是否一一對應。經典概率論和量子理論只是作為其中的特例出現。廣義概率論旨在通過通用的概率關聯性語言和操作要素研究不同的物理理論，體現了器件無關原理的中心思想。該理論作為一種操作工具，有助于人們利用其對不同理論的物理原理展開調整或修改，從而復現量子物理的基本結構。

2001 年文獻[28]提出通過5 個公理推導量子物理。為得到與設備無關的廣義操作模型，文章研究最普適的量子演化類型，將典型的實驗場景概括為3 個部分：制備裝置、變換裝置和測量裝置。這一普適化的實驗框架為GPT 理論的發展和豐富奠定了基礎。

1.2 盒世界理論 (box world)

GPT 理論通過一些簡明扼要的公理刻畫物理理論，試圖從通過對這些公理進行微調找出量子理論的物理特性。盒世界理論作為其中非定域性最強的理論，在對比研究量子理論方面具有十分重要的研究價值。盒世界理論是一個僅由“無信令”原理刻畫的理論，其概念起源于根據相對論因果關系提出的一種稱為PR box 的無信令物理模型[19]。該模

2009 年，文獻[30]對盒世界理論的測量空間進行了全面詳盡的研究。文章指出，盒世界理論中有一類稱為“基本測量”(basic measurements)的系統測量，可以分解為一系列順序作用于子系統的基準測量，且基準測量之間存在明確的關聯。后面執行的基準測量xi∈{0,1}選擇取決于前一個測量ai?1∈{0,1}的 結果，且最終的系統測量結果r可以看作基準測量結果a的 函數r=f(a)。總的來說，基本測量可以看作是一套具有確定順序的系統測量方案。如圖3，以一個作用于兩體系統的基本測量m1為 例，m1可以分解為如下過程：首先選取基準測量x2=0作用于子系統Bob，并產生第一個基準測量結果a2。接著進行第二個子系統Alice 基準測量，其測量選擇等于第一個基準測量結果，即x1=a2， 最后，系統結果r由函數r=a1給出。其數學描述如式(6)，元素m(a1,a2|x1,x2)=1表示執行結果為a1,a2的系統測量x1,x2。根據基本測量中的關聯性x1=a2=0/1，可以得出，所有實現的分量中若m(a1,a2|x1,x2)=1，則一定存在非零元素

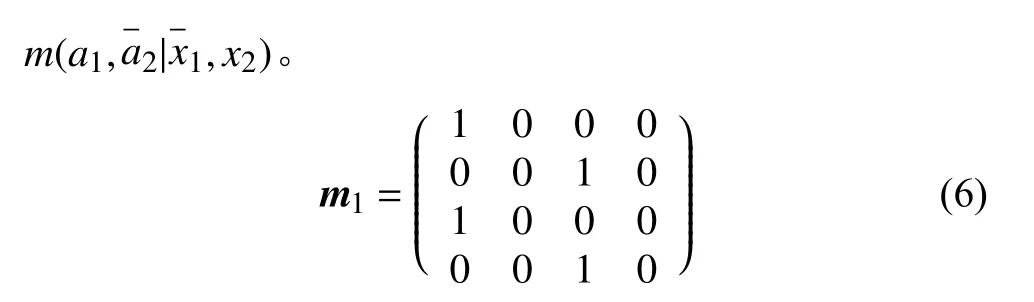
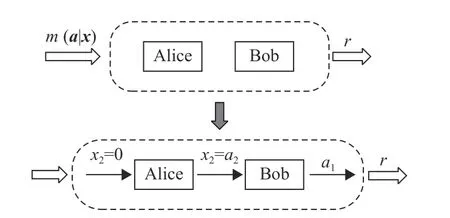
圖3 兩體系統基本測量示意圖

該文章證明當物理系統為單體或兩體系統時，盒世界理論中的所有有效測量都可以看作是基本測量的凸組合。其中，單體系統的所有合法測量都對應一個等價的基準測量，符合基本測量的定義。換句話說，單體或兩體系統中的合法測量都可以分解為一系列輸入與其他輸出相關聯的基準測量的凸集合。然而，這種直覺上順理成章的定理在三體及以上的多體盒世界理論中卻不成立。文章指出，三體系統中存在無法分解成基本測量的合法測量。文獻給出如下示例，測量m2是一個合法的三體系統測量。通過矩陣表示可知，實現的測量分量有m(001|000),m(110|000),m(000|100),m(100|100),m(101|010),m(111|010),m(010|001),m(011|001)。可以看到所有執行的測量ai及 結果xj中 ，并無關聯性存在。m2無法通過基本測量復原，是一類特殊的合法測量。

文獻[30]的發現使物理界開始關注合法態空間和合法測量空間之間的平衡關系。此外，盒世界理論在態空間和測量空間上極大的非定域性反差使得該理論在解決計算問題方面的能力變得撲朔迷離，盒世界理論會擁有比量子理論更強大的計算能力，亦或是和經典理論不相上下？

為探究這一問題，文獻[36]從算法的角度重新解讀GPT，定義與之相對的計算操作電路，試圖分析這類基于基本物理原理的廣義理論的計算能力，和量子理論一決高下。文獻[73]將GPT 框架內任意理論G 能有效解決問題的復雜度類定義為BGP。當理論G 指定為量子理論時，該復雜度類特指BQP[73]；若理論G 指定為經典理論，則復雜度類相應地類比為BPP。文章證明BGP 類包含于經典復雜度類AWPP[74](A WPP ?PP ?PSPACE) 中，即BGP ?AWPP ?PP ?PSPACE。事實上，AWPP 經常出現在量子計算背景下，AWPP 是BQP 計算上限的最小經典復雜度類。文章的結論表明，量子理論中已知的結論 B QP ?AWPP[75]在GPT 中普遍存在，任何遵循層析定域性(tomographic locality)，即復合系統的狀態可以由定域的測量刻畫的理論都包含于AWPP 內。不僅如此，一些僅遵守層析定域性而違背“無信令”因果原則的理論也存在這樣的結論。這一結論為量子計算帶來全新的思路：不受因果律限制的量子理論或許可以有效解決某些對現有量子計算機來說很難的問題[76]。

除此之外，研究證明具備對測量結果進行后選擇(post-selection)能力的量子理論復雜度類PostBQP等價于概率圖靈機(probabilistic Turing machine)在多項式時間內可解決的一類決策問題PP，即PostBQP=PP。由PostBGP ?PP 可以得出，任意遵循層析定域性的后選擇GPT 理論PostBGP 能夠有效解決的問題都可以被后選擇量子計算機有效解決。因此在后選擇前提下，量子理論在所有GPT理論中是最優的理論。另一方面，文獻[37]提出，若放寬對量子態的限制，存在一個由層析定域性和“無信令”因果性刻畫的非理論G，使得BGP=AWPP，且BQP 無法到達該邊界。這表明AWPP 服從因果律，任何非因果的層析定域理論都可以由遵循因果定律的計算模型有效模擬。該結論清晰地闡述了非定域關聯性和計算能力之間的關系，非定域性越強的理論在計算能力上有越強的優勢性。

這一系列針對計算復雜度的理論研究一方面從信息論的角度提取GPT 理論的物理特性，總結物理原理；另一方面分析所有非定域關聯性集合的計算能力，致力于探究量子計算優勢的物理源頭，并將該計算優勢合理最大化，為尋找更多的存在量子加速的算法提供指引。

2 三大量子原理

歸根結底，GPT 框架研究的最終目的是將已知的物理原理放在包括態制備、演化、測量的統一操作框架下推導出一系列與量子理論相似的物理理論，并通過對物理原理對應的數學描述進行微調使其最終成為量子理論。另一方面， PR box利用描述量子關聯性的Bell 廣義模型從量子力學中提煉和相對論因果律相關的“無信令”原理[19]。這項工作為尋找量子物理的信息原理研究提供了另一種思路：根據物理理論在系統中產生的關聯性進行分類和研究，從中抽象出物理原理。這種方法僅從觀察到的統計數據中考慮原理，而無需對系統進行任何理論建模。盡管“無信令”原理的研究表明兩者無法完全刻畫量子關聯性，但仍激發了物理學家們繼續探索一種具有深刻洞察力的物理原理，為量子關聯性的非定域程度做出直觀解釋[39,77]。經過一系列的探索，物理學家們總結出器件無關原則下的三大物理原理：信息因果原理、宏觀定域原理和定域正交原理。這些物理原理試圖從不同角度證明量子理論之外的關聯性違反這些合理原則。

2.1 信息因果原理(information causality)

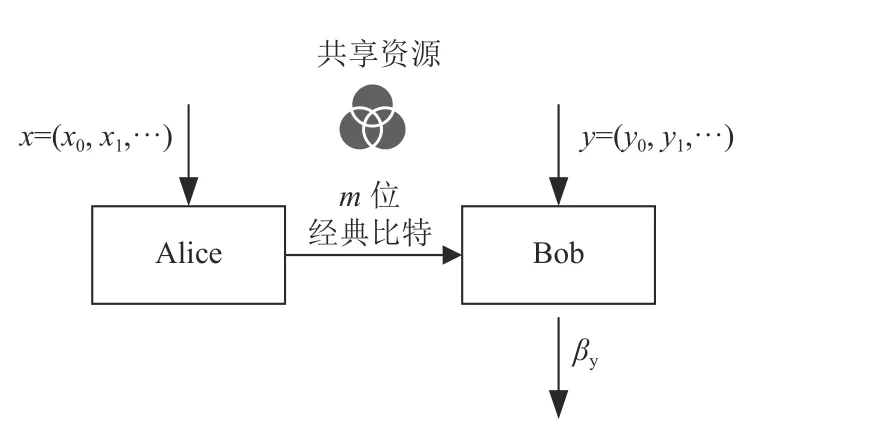
圖4 隨機訪問編碼任務示意圖

為了排除盒世界等非定域性強于量子關聯性的理論，文獻[38]對共享資源提出限制，要求共享的資源不能提供Alice 有關x的任何信息，并提出信息因果原理的明確定義：利用所有的本地資源和帶寬為m比 特的經典信道，Bob 可以最多獲得m比特關于Alice 未知數據的信息。為進一步量化Bob和Alice 之間的共享信息，定義Bob 輸出數組 βy攜帶關于xy信息量的互信息(mutual information)為：

信息因果原理可以在(2,2,2,2)實驗中復現Tsirelson 界限[80]，從而從眾多GPT 理論中挑出量子理論，這使得信息因果原理被許多物理學家視作量子理論基本原理的候選。在把它當作量子物理的基本原理之前還有一些問題需要進行深入研究。一方面，違背信息因果原理的必要條件尚不清楚[81]；另一方面，將其應用于多體量子系統的方案實現也困難重重[82]。但不可否認的是，信息因果原理是量子理論擁有的自然屬性，是區別于其他非定域關聯性的重要物理依據。

2.2 宏觀定域原理(macroscopic locality)

物理學家們嘗試通過建立量子理論和經典理論之間的關聯獲得對物理原理更深刻的理解，宏觀定域原理的概念由此而來[40]。這一概念主張任何物理理論在宏觀極限中都應該可以被經典物理描述。研究表明，微觀結構宏觀化的一個重要手段是粗粒化(coarse-graining)。通過減少描述動力系統的演化方程組，量子理論允許在測量值足夠粗粒度時被經典動力學描述[83]。宏觀極限下的量子系統將不再以粒子作為研究對象，取而代之的是對粒子束的探測。因此，粗粒化處理之后的測量結果為粒子束的強度分布。以兩體系統為例，設兩體系統可能的輸

2.3 定域正交原理(local orthogonality)

2.4 “Almost quantum”理論

這一系列基于量子關聯性展開的物理原理研究始終圍繞一個關鍵的問題：是否可能存在一些物理原理能夠從所有可能的關聯性集合中唯一地識別出量子關聯性？想要肯定回答這個問題則需要找出量子概率關聯性與其他關聯性的區別。然而，2015年文獻[43]提出一個包含量子關聯性的理論，稱為“Almost quantum”。該理論證明在各種不同的關聯性理論中，量子理論并不那么特殊。

雖然Almost quantum 是一個嚴格大于量子力學的理論，但有證據證明Almost quantum 集合滿足大多數試圖刻畫量子關聯性的物理原理，包括信息因果原理、宏觀定域原理和定域正交原理。例如，對兩體系統而言，Almost quantum 關聯性等價于NPA 層次結構中的第1+AB級關聯性集合Q1+AB。而關聯性集合滿足定域正交原理的充分必要條件是屬于NPA 結構的第一級集合 Q1。由NPA 的結構特點可知，Q1集 合包含Q1+AB集合，Almost quantum 理論完全滿足定域正交原理。并且根據現有數值結果，有理由猜測Almost quantum 理論能夠完全符合信息因果原理與宏觀定域原理。因此，這些原理都不能充分描述量子關聯的非定域程度。從某種程度上說，僅僅通過定義態空間關聯性的物理原理只能止步于表征Almost quantum 理論，無法更加接近量子物理的真相。此外，研究表明盡管Almost quantum 和量子理論的態空間十分相似，但Almost quantum 理論的測量空間中存在一些無法排除的不合法測量。文獻[92]試圖在GPT 理論框架下重現Almost quantum 關聯性，發現若存在這樣的理論，它將不滿足無限制假設(the no-restriction hypothesis)，該假設規定GPT 理論中的合法測量集是態集合的對偶。這一結論更進一步印證了量子物理中態和測量空間的特殊性。想要準確定義量子關聯性，還應該進一步限制系統上可能測量的規則。

總而言之，物理學家們嘗試在量子理論的物理特性中總結出規律，并使其成為不拘泥于某一特定理論形式的物理原理，最終重構量子理論的物理邏輯。這個過程中有兩個主要的研究路線。一方面，通過GPT 中可操作的公理基礎推導量子力學的理論結構。另一方面，從概率關聯性空間中提煉相關的物理原理，在任何可能的關聯性集合中篩選出量子關聯性。

在所有器件無關原理和GPT 廣泛操作框架研究中，具有抽象含義的黑盒模型是貫穿其中的基本思想。這樣一種最普遍的模型可以用于任意物理理論，在統一的理論背景對各種不同理論進行平等比較，更好地了解量子理論的特性。另一方面，黑盒思想促進了人們對因果律的認識。物理學家們僅要求黑盒的內部遵循某一特定物理理論，針對黑盒間的信道組合展開一系列研究，嘗試在現有因果律下對其進行解釋。

3 不確定因果順序 (indefinite causal order)

“無信令”原理作為黑盒思想下一個十分重要的物理原理，是GPT 操作框架下的基本原理。該原理來自量子理論中對相對論因果律的一個自然描述，要求任何物理理論條件下，黑盒之間的信道都具有明確的因果關系。然而， PR box 的研究表明，“無信令”原理作為唯一描述量子理論的物理原理不夠的，且在此基礎上的一系列補充和調整都沒有完全成功。與此同時，一些物理學家們開始試圖將黑盒內部限制為已知的物理理論，而不對黑盒之間的組合方式做明確要求，只通過黑盒的輸入輸出信息重構黑盒間遵循的因果關系。

因果關系可以理解為定義一系列事件發生的先后順序。如圖5 表示復合系統中若存在Alice 發送信號給Bob 的信道，則視為事件A是事件B的因果過去(causal past)，表示為 A ?B，或者說事件B是事件A的因果未來(causal future)，表示為B?A，且事件先后順序的固定使得AB之間限制為單向傳輸，即B?A。通常來說，兩體系統具有預定義因果順序(predefined causal order)表示聯合概

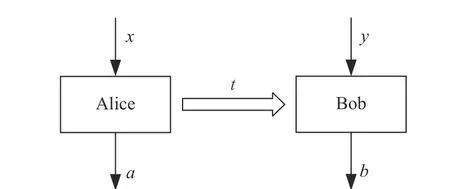
圖5 確定因果順序 A ?B的兩體系統示意圖

3.1 量子系統中的不確定因果順序

2012 年，文獻[44]量子電路中的因果律提出新的設想，構造了一個摒棄全局因果順序的量子電路。該基本框架包括3 個假設：1) 隨機變量，每個實驗室的輸入變量是自由隨機選擇的；2) 封閉的實驗室，實驗室生成輸出的過程不受外界環境和其他實驗室的影響；3) 局域量子性有效，規定每個實驗室內部遵循量子力學，但不對整個復合系統做要求全局要求。該研究繼續沿用器件無關思想，將每個實驗室看作是具有有限輸入和對應輸出的黑盒，在此基礎上研究因果結構對量子關聯性的影響。

為測試框架內的系統關聯性是否真的存在未預定義的因果順序，文章設計了一些模型用于因果結構的量化比較。如圖6，以兩體系統為例，假設Alice 和Bob 分別具有隨機輸入x,y(x,y∈{0,1})，通過一系列本地操作之后，a和b將分別作為系統Alice，Bob 的輸出值(a,b∈{0,1})。同時，規定物理系統中存在隨機變量b′(b′∈{0,1})作為“裁判”，用于判定Alice 或者Bob 是否成功猜測對方輸入值，即a=y或b=x。在這當中，我們假定Alice 可以通過單信號通道將實驗信息發送給Bob(Alice ?Bob)。因此，物理系統成功的概率可以通過數學公式表示為：

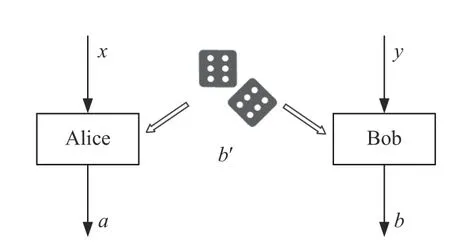
圖6 因果不等式示意圖

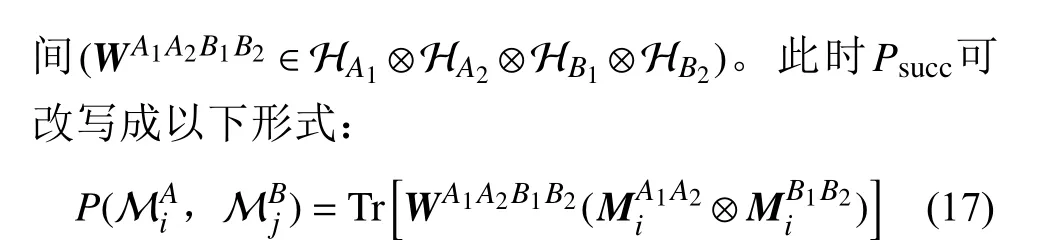
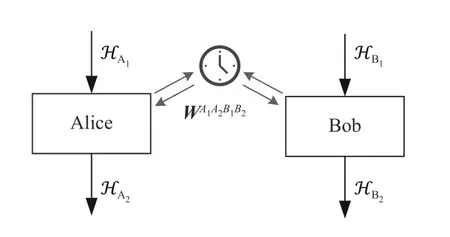
圖7 不預定義全局因果順序的量子兩體系統示意圖

3.2 經典系統中的不確定因果順序

文獻[44]提出的因果框架引發諸多關于過程矩陣與因果模型之間的研究[95-97]，其中關于經典極限下兩體系統必然存在確定因果順序的結論引發質疑。研究發現，在三體或多體系統中，可能存在一些與任何預定義因果順序都不兼容的信道[46]。文章設計了一個因果博弈游戲，該游戲在具有預定義因果順序的場景中獲勝概率嚴格小于1，但在沒有預定義因果順序的情況下一定獲勝。并證明，在局部兼容經典概率論的三體系統中，存在特殊的過程矩陣使因果博弈游戲始終能夠獲勝。2015 年，文獻[47]對經典系統中的因果順序進行了數學刻畫與深入分析。

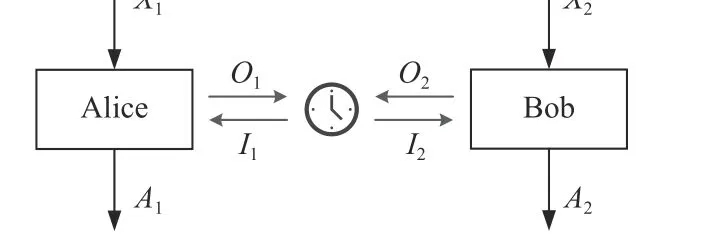
圖8 不預定義全局因果順序的經典兩體系統示意圖

由于在任意本地操作下系統的總測量概率為1，且測量概率非負，因此可以得出，在兩體經典系統中，所有局部適用經典概率論的模型滿足以下要求：以等價為以下形式，3 個實驗室之間相互影響，互為因果，形成因果循環(如圖9)，不能用預定義全局因果順序解釋。

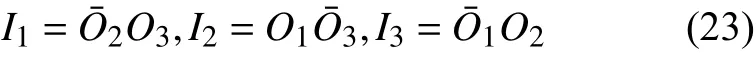
3.3 量子電路的經典控制與量子控制

此外，固定因果順序的量子電路中存在一類特殊的量子電路：具有并行操作的量子電路W||(quantum circuits with operations used in parallel, QCPARs)。該電路中存在多個可以同時進行的操作電路，以任意可能的固定順序將操作應用于內部映射，在輔助系統的額外幫助下得到相應輸出的過程，所有操作有且只能執行一次。

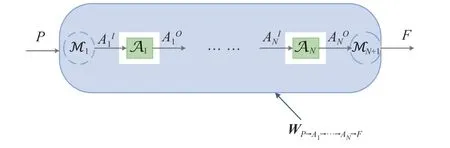
圖10 固定因果順序的量子電路示意圖

圖11 經典開關電路示意圖

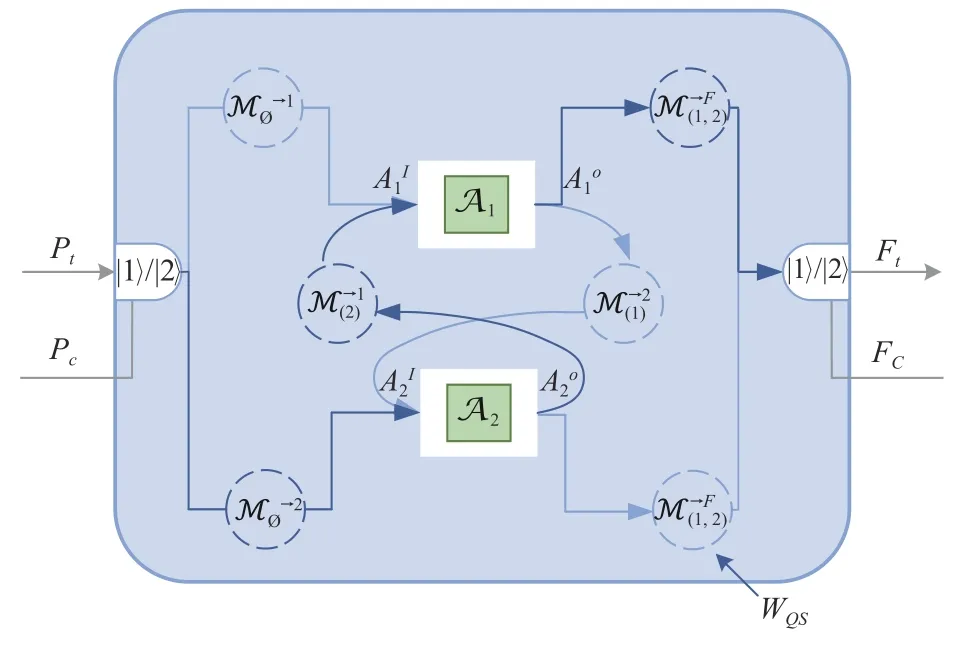
圖12 量子開關電路示意圖

總而言之，以上3 類量子電路對應的量子超映射都是具有確定的超映射，因此又被稱為“超信道”(superchannel)[122]。這類超映射具有保跡性，若將要求進行適當的放松改為跡非增映射，則可以得到概率過程矩陣。若一組概率過程矩陣之和為一個確定過程矩陣，則稱之為“量子超器具”(quantum superinstruments)[123]。

如圖13，不同量子電路的特點與關系總結如下。首先，固定因果順序的量子電路是最小的集合，包含一個確定因果順序的電路，且所有過程矩陣具有因果可分性[97,124-125]。然而，QC-FCs 并不是一個凸集，通常情況下不同順序的QC-FCs 的凸組合并不是一個合法的QC-FC，不能用一個簡單的確定因果順序電路模擬。然而，具有并行操作的量子電路W||是一個例外。根據定義可得，QCPARs 與任何順序的QC-FC 兼容。其次，經典控制因果順序的量子電路作為一個凸集包含QC-FCs，其過程矩陣仍具有因果可分性，其中典型代表是經典開關WCS，能夠利用經典比特離散地控制因果順序。值得注意的是QC-CCs 并不是多個QC-FCs 的簡單概率混合，過程矩陣WQC?CCs等式中的任何一個子項W(k1,k2,···,kN,F)都不滿足合法性條件。最后，量子控制因果順序的量子電路是QC-CCs 的拓展，典型電路包括量子開關WQS。QC-CCs 與QC-QCs都是動態建立因果順序的量子電路，后面的量子操作順序取決于之前的操作[95,97,99,124]。此外，這兩類過程矩陣都是因果可分的，不能違背因果不等式。因此，QC-QCs 不包含文獻[44]提出的量子模型WOCB，是所有合法量子超映射的真子集。

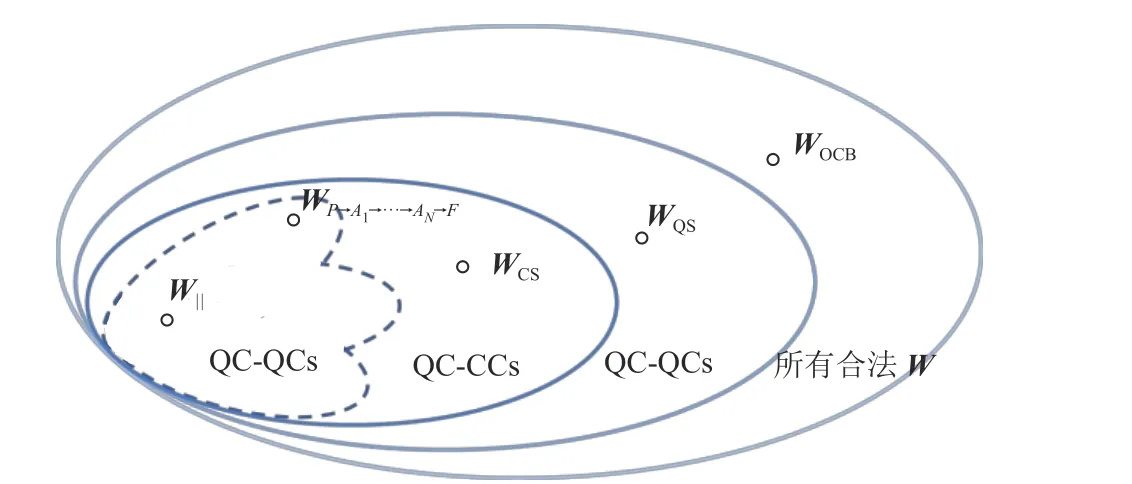
圖13 過程矩陣分類圖[49]

關于量子電路的操作控制的研究可以為嘗試設計各種實驗以實現不確定因果順序的模型提供理論基礎。不難看出，這種通過自下而上的方法構建廣義量子電路的研究仍存在一些開放性問題，如QCQCs 類之外的量子超映射是否具有物理解釋？具有何種性質？

4 結 束 語

尋找量子物理的信息原理是圍繞量子理論的根本問題而展開的基礎研究，試圖以物理的角度看待由希爾伯特空間等數學語言描述的量子理論，從中抽象出最基本的原理，解釋薛定諤方程背后的物理意義。“無信令”原理作為第一個從量子理論中總結出來的反映相對論因果性的器件無關原理，是整個研究的基礎。一方面，GPT 規定框架內的所有公理推導遵循“無信令”原理，所有黑盒之間具有確定的因果關系。GPT 作為一個普適的操作框架，有利于在統一的理論背景下對公理推導而來的理論結構進行公平對比，并通過部分修改還原量子理論的特性和邏輯結構。另一方面，“無信令”原理作為Bell 概率模型的延伸，描述了量子關聯性的重要特征。有關“無信令”原理的研究激勵著更多物理學家從關聯性中提煉能夠唯一識別量子關聯性集合的所有物理原理，將其與其他關聯性集合完全區分開來。這種方法不再考慮通過操作公理推導理論結構，僅從觀察到的統計數據中考慮原理。然而，另一項研究有著和“無信令”原理完全相反的思維邏輯。不確定因果順序結構在特定的物理理論限制下，通過放寬對黑盒間信道的全局假設，允許其在不違背該理論數學描述的前提下出現不同的組合方式。該研究可以證明，目前人們對于因果律在量子理論中的物理描述并不完全清楚。這一發現或許可以為完善量子物理原理的基礎研究提供新的思路。

回顧尋找量子物理的信息原理之路，有一些跡象表明，當前研究無法準確定義量子關聯性的原因可能在于我們將滿足全局因果關系的黑盒子與滿足特定物理描述的黑盒子當成兩個不同的問題來研究。也許在數學中無處不在的對偶思想在量子物理的基本原理上還沒有得到很好的體現[126]。黑盒子與因果律的關系也許比我們現階段了解到的還要更近一些。