精確Grover 量子搜索算法概述

李冠中，李綠周

(中山大學計算機學院 廣州 510006)

求解無序數據庫搜索問題的Grover 量子搜索算法[1]于1996 年被提出，相對于經典算法有平方級別的加速。自問世以來，得到廣泛應用，如被用于求解最小值查找問題[2]、串匹配問題[3]、量子動態規劃[4]及計算幾何問題[5]。不僅如此，針對Grover算法本身的擴展也不少，如量子振幅放大[6]、圖上量子游走搜索[7]、不動點量子搜索[8-9]及本文要介紹的精確Grover 量子搜索算法[6,10-11]。

1 原始Grover 算法及其缺陷

無序數據庫搜索問題可以抽象地描述如下，在大小為N=2n的 無序數據庫中，有M個元素是符合要求的，這些目標元素通過一個函數f:{0,1,···,N?1}→{0,1}來 標識：若編號為x的元素為目標元素，那么f(x)=1； 否則，f(x)=0。假設有一個可以識別搜索問題目標元素的黑盒：要判斷編號為x的 元素是否為目標元素，只需要將編號x輸入黑盒，它就會輸出f(x)的值。現在希望以盡可能少的黑盒調用次數(稱之為查詢復雜性)，找出一個目標元素。

在量子計算中，實現函數f(x)的黑盒的作用效果是一個酉操作Of，其在計算基態上的作用效果為：

2 精確Grover 量子搜索算法

2.1 大步小步

2.2 共軛旋轉

2.3 三維旋轉

這一方法[11]的思路為：把G(?,?)在 正交基 |A〉和|B〉下的二維酉矩陣對應到相應Bloch 球中的三維旋轉，再通過選取適當的角度 ?和旋轉次數k，使得Gk(?,?)|ψ〉在 該Bloch 球面上與 |B〉重合。

具體來說，由于任意二維酉矩陣都可以寫成下式右邊的形式，因此令

由 于 初 態 |ψ〉在Bloch 球 中 對 應 的 向 量 為s:=[sin(2θ),0,?cos(2θ)]， 而算法最終欲得的 |B〉對應的向量為t:=[0,0,1]， 故 〈n|s〉=〈n|t〉 。 這說明s和t在Bloch 球面以n為軸的同一個的圓上，所以確實可以通過繞固定軸n進行多次旋轉，把s轉 到t。為了確定參數 ?和旋轉次數k， 記r為s和t在n上的投影，如圖1 所示，解析幾何計算表明s?r和t?r之間的角度為 ω=π?2β。根據之前的推導，每作用一次G(?,?)相 當于繞轉軸n旋 轉 α =4β， 而 ω是所希望的總旋轉角度，因此令ω =kα 可以求出 ? 與k應該滿足關系式：

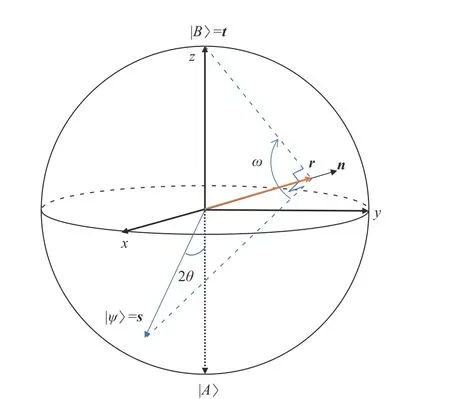
圖1 在{ |A〉,|B〉}的 Bloch 球中，G (?,?)的多次作用相當于把初態 s 繞 轉軸 n旋 轉到目標元素的均勻疊加態t

容易驗證，圖2 和圖3 分別展示了S f(φ)和Sψ(?)的電路實現，其中最后一行為輔助qubit。注意到S f(φ) 需 要調用兩次黑盒Of，因此表1 中后兩種方法的黑盒調用次數是原始Grover 算法的兩倍，不過這并不影響平方加速的數量級。

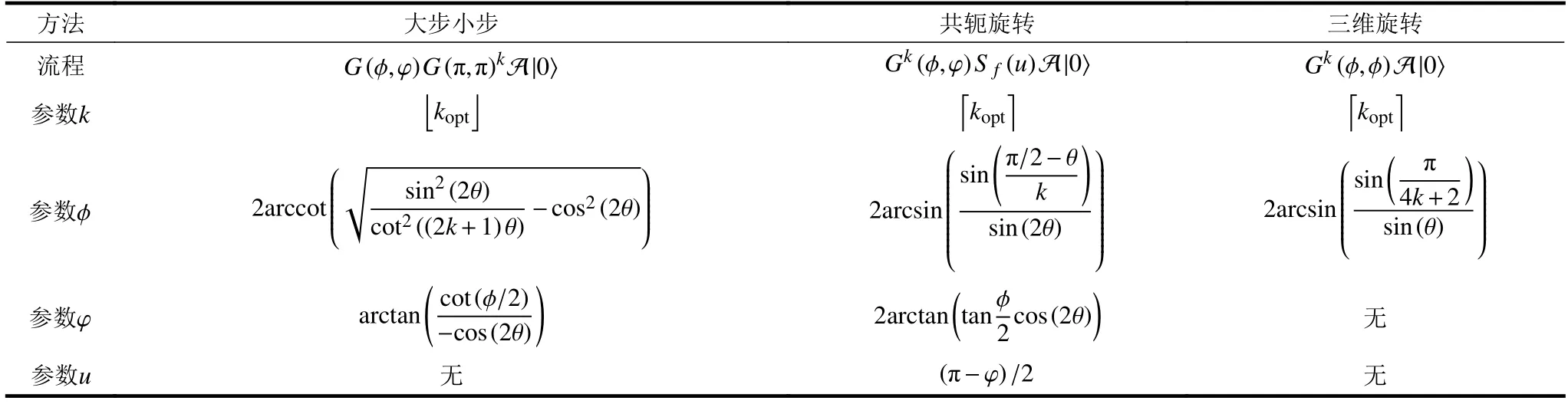
表1 3 種精確Grover 量子搜索算法

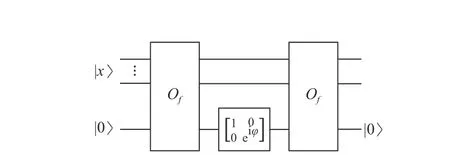
圖2 S f(φ)的 電路實現，其中Of|x〉|b〉=|x〉|b⊕f(x)〉

圖3 S ψ(?)的電路實現

3 精確量子搜索的查詢下界

3.1 目標元素占比未知時的查詢下界

3.2 目標元素占比已知時的查詢下界

在目標元素的占比已知的情況下，利用文獻[14]的quantum angle 方法，并把它直接地擴展到多個目標元素的情形(即文獻[15]文末提及的選取?N/M」個“不相交”數據庫的思路)，可以證得精確量子搜索的查詢下界為

4 結 束 語

本文梳理了3 種精確Grover 量子搜索算法，給出了算法流程、參數設置以及背后的幾何直觀，并指出它們都依賴于目標元素的占比，由此為出發點，說明了算法的最優性：對于目標元素占比已知的情況，3 種精確Grover 量子搜索算法已經達到最優；而對于目標元素占比未知的情形，精確量子搜索算法相比經典算法沒有加速。因此本文對精確量子搜索算法給出了較為完整的概述。