基于Profile 比對的改進星比對算法

陳俊濤，鄒 權

(電子科技大學基礎與前沿研究院 成都 610054)

多序列比對是生物信息學研究中重要的課題之一，對于識別未知基因功能、分析物種間的進化關系、識別基因之間的保守區域等問題有著重要作用。隨著測序技術的發展，基因序列數據快速增長，現有軟件難以處理大規模的多序列比對問題。

目前大多數軟件采用的是漸進式比對策略或者迭代式比對策略[1]，如MAFFT[2]、Kalign3[3]、Clustal[4-5]、MUSCLE[6]、T-Coffee[7]、HAlign[8]等。漸進式比對需要先計算兩兩序列之間的距離，再根據距離矩陣使用層次聚類算法，如UPGMA、Neighbor Joining 等構建一顆比對的指導樹，沿著指導樹的枝干進行兩兩比對與合并，最后得到最終結果。而迭代式比對策略在此基礎上，還要對合并的最終結果選取適當的策略，如剪枝、局部重新比對和隨機選取序列重新比對進行迭代，直到比對精確收斂或者迭代次數達到上限。迭代式比對策略可以解決漸進式比對初期可能遺留下的問題。因為漸進式比對策略是貪心策略，在初期局部的比對結果上可能陷入局部最優，而錯誤會一直保留至最終結果中。而通過迭代式比對可以選取適當的策略，去更正局部比對的一些錯誤，但迭代式比對增加了時間復雜度。這兩者都有著較高的時間復雜度，所以難以在有限時間內處理大規模數據的比對。

漸進式比對策略的時間復雜度與序列數量呈多項式級增長，因此在面對大規模數據的情況下，該策略時間復雜度太高、比對時間過長。而星比對是一種啟發性的策略，其時間復雜度與序列數量呈線性增長，這有效降低了大規模序列比對的時間。然而，星比對算法在相似度不高的數據集上的比對精度較低，目前只能應用到相似度非常高的同源序列上，這大大限制了星比對的應用。

針對星比對精度低的問題，本文將漸進比對的模式應用于星比對中，提出了基于profile 比對的改進星比對算法。實驗證明改進后的算法提高了比對的精度，同時也節省了比對時間。

1 算 法

本研究改進的星比對算法采用了漸進比對的思想，先構建一顆比對的指導樹，然后沿著樹的枝干進行比對。但是與傳統的構建指導樹的方法不同，本研究沿用了星比對的核心思想，即中心比對的思想。為了加快比對速度，引進了k-band 策略以加速雙序列之間的比對。

1.1 雙序列比對

對于雙序列比對問題，主要采用動態規劃的方法，有全局比對Needleman-Wunsch 算法[9]和局部比對Smith-Waterman 算法[10]。

圖1 展示的是全局比對算法，即先建立一個得分矩陣然后根據計算規則計算最大得分(匹配+1、不匹配?1、空格?1)，再從右下角的最大得分回溯至左上角，得到最優比對。

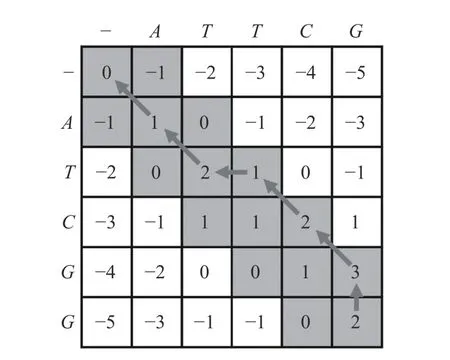
圖1 DNA 雙序列比對動態規劃算法

本研究采用的是仿射罰分與k-band 結合的雙序列全局比對算法[8]。不同于圖1 的線性罰分，仿射罰分的機制更為合理，這有效地避免了間斷出現缺失的情況，使得比對結果更傾向于連續出現缺失，這也更符合生物學的進化過程，即一旦缺失位點出現，那么此位點就會有更大可能性再次出現缺失。k-band 策略指的是兩條序列較為相似時，回溯路線一般會在對角線附近，非對角線附近區域的值可以不用計算，只用計算對角線附近的寬為k的帶，這個寬為k的帶被稱為k-band。k-band 這一啟發性策略減少了比對的時間和空間復雜度，將時空復雜度由O(pn)降 低到了O(kn)(p和n為序列的長度，k為帶的寬度)。如圖1 所示，回溯路徑只出現在k=1的 灰色帶中。k的 初始值一般為p和n的差值的絕對值，然后進行k值的迭代，計算比對的最優得分，每次迭代k值翻倍，直到得分最大值收斂則停止迭代。

雖然采用k-band 策略的雙序列比對算法可以減少算法的時間和空間復雜度，但是不能確保找到最優的比對，有可能會陷入局部最優解中。為了減少此類情況的發生，只對序列長度相近的序列采取k-band 策略的比對，對于序列長度相差較大的序列則采取全局比對的方法。因為兩條序列長度相差較大，可能會導致k值迭代后的k-band 的區域很大，甚至超過原本pn大小的區域面積，不僅無法節省時間和空間，反而需要更大的時空復雜度。

1.2 傳統的星比對算法

傳統的星比對算法主要分為以下3 個步驟：

1)選取中心序列；

2)將中心序列與其余序列一一進行比對；

3)根據“once gap, always gap”的原則，將雙序列比對的結果合并，得到最終的比對結果。

中心序列的選取是傳統星比對算法步驟中時間復雜度最高的，因為需要計算兩兩序列之間的相似度。傳統計算序列兩兩相似度的方法是動態規劃，時間復雜度為O(n2)。但是由于其復雜度太高，目前使用較為廣泛是使用k-mer 法計算序列相似度，其時間復雜度為O(n)。使用k-mer 計算序列間的相似度，選取中心序列的總體復雜度可降為O(m2n)，其中m為序列的條數，n為序列的長度。步驟2)需要將中心序列與其余序列一一做比對，其算法時間復雜度為O(kmn)。步驟3)合并序列比對結果的算法時間復雜度為O(mn)。結合3 個步驟的算法時間復雜度，該算法的總體時間復雜度為O(m2n+kmn)。

1.3 改進的星比對算法

本研究對傳統的星比對算法進行了改進。首先，參考了cd-hit[11]聚類軟件的思路，將最長的序列作為中心序列。然后，引進了漸進比對的思想，將構建指導樹和profile 比對的策略加入到改進的星比對中來。

改進的星比對算法主要有以下4 個步驟：

1)選取最長序列；2)計算最長序列與其余序列之間的相似度；

3)根據步驟2)得到的相似度構建比對的指導樹。構建指導樹的原則為，先將相似度最高的序列聚合，再依次根據相似度，將序列加入樹中，最終構建一顆單鏈指導樹；

4)沿著指導樹進行比對和合并，最終得到比對結果。

圖2 展示了構建指導樹和比對的過程。本研究將序列中的最長序列作為中心序列，這大大降低了選取中心序列的時間。改進后的星比對算法，雙序列比對只會在首次比對的時候出現，在指導樹的枝干上都是序列與profile 比對。與雙序列比對不同，序列與profile 比對計算得分耗時會更長，在一定程度上會增加比對的時間。因此，改進后的星比對算法的時間復雜度與序列數量不呈現線性增長，其增長速度介于漸進比對和傳統星比對之間。

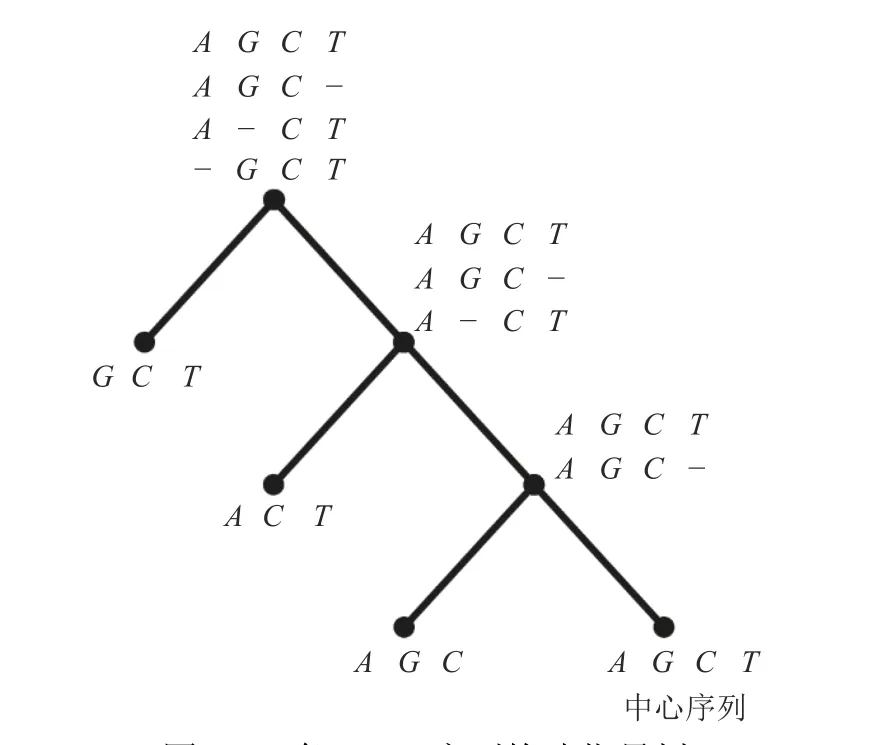
圖2 4 條DNA 序列構建指導樹

2 實 驗

本研究采用了模擬的RNA 數據來驗證算法的有效性。根據序列數量將數據集分5 個組，序列數量 分 別 為：256 條、512 條、1024 條、2048 條、4096 條，序列平均長度約為1500 個堿基對。每個組分別有20 個不同數據集，測試多數據集以求取精度的平均值，可以驗證算法的魯棒性，避免因為偶然性影響實驗結果的有效性。實驗數據來自于公開數據集網站https://kim.bio.upenn.edu/software/csd.shtml.

實驗采用了SP score 來衡量多序列比對的效果，該值是多序列比對中所有雙序列組合的比對得分之和。雙序列計算得分規則為：相同位置字符匹配則得1 分，不匹配或者兩者都是空格則得0 分。SP 分值越高則代表比對的效果越好。而在數據較大的時候，SP 值過大不能準確展示其精度，因此本研究采用了SP 值的平均值來展示比對精度。

本研究對傳統的星比對算法做了兩項改進：1)改進選取“中心序列”的策略，以降低選取算法的時間復雜度；2)引進了漸進比對的思想，構造一棵特殊的指導樹，加入profile 比對的策略。為了研究兩項改進對比對精度的影響，本文設計了4 種實驗的算法組合：傳統的星比對算法+傳統的中心序列選取策略、傳統的星比對算法+選取最長序列、改進的星比對算法+傳統的中心序列選取策略、改進的星比對算法+選取最長序列，比對4 組實驗的精度和時間。4 組實驗都是在CPU 為Xeon E3-1230，內存為32 G 的Ubuntu 20.04 系統環境下進行的。

實驗結果如圖3 和圖4 所示。圖3 展示了4 組算法在不同數據集上的精度。可以看到隨著數據集的增大，比對的精度也隨之降低。

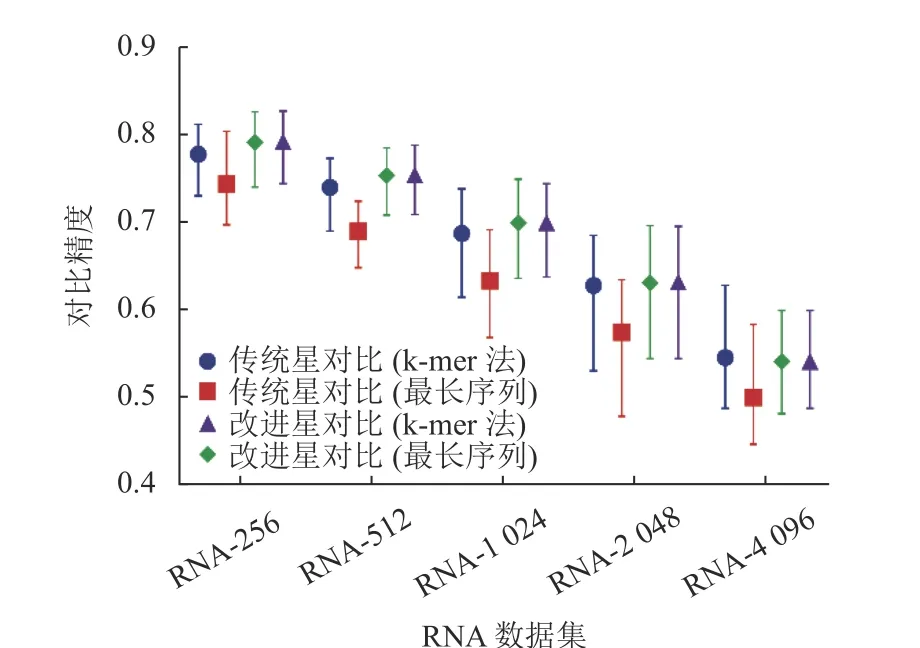
圖3 不同數據集的比對精度對比

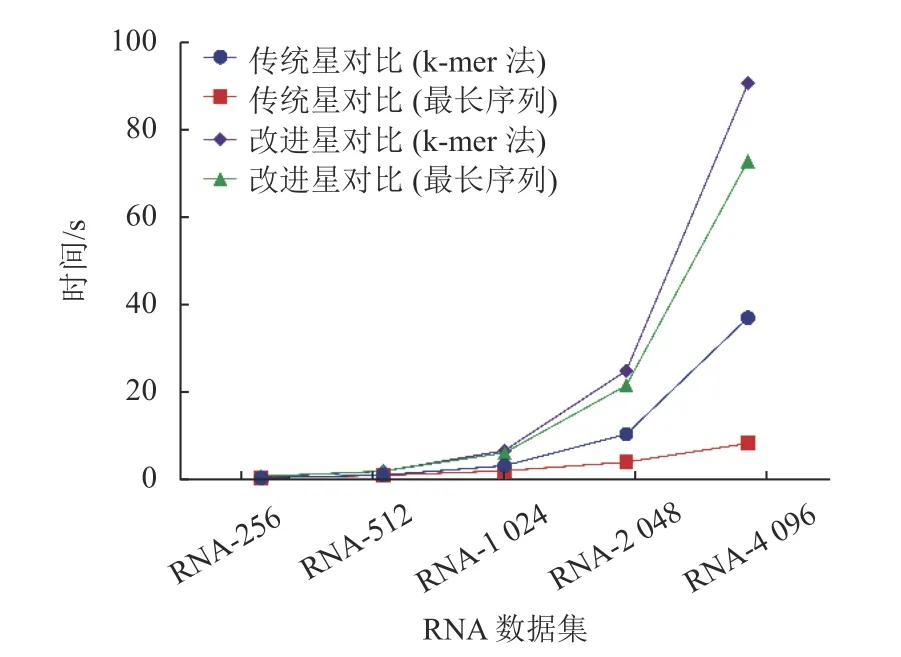
圖4 不同數據集的比對時間對比

在使用傳統的星比對算法的基礎上，對比使用不同的選取中心序列的策略。使用k-mer 法計算相似度選取中心序列的策略明顯優于使用最長序列計算相似度的策略，可以觀察到在5 組數據集中，使用最長序列策略的比對精度都要比傳統的策略低。而在使用改進的星比對算法的基礎上，兩種選取中心序列的策略得到的比對效果近乎一致，無論是在比對精度的均值還是在比對精度的范圍上，兩者并無明顯差異。

在使用傳統策略選取中心序列的基礎上，改進的星比對算法的比對精度明顯要優于傳統的星比對算法。同樣，在使用最長序列作為中心序列的基礎上，改進的星比對算法的比對精度也明顯優于傳統的星比對算法。

由圖3 可知，在4 組實驗中，可以看到改進的星比對算法的比對效果優于傳統的星比對算法。從圖4 可知，使用最長序列作為中心序列的策略，可在一定程度上減少比對的時間。因此改進的星比對算法加上使用最長序列作為中心序列的策略是最佳的組合方式，此組合可以得到最好的比對精度，同時不會顯著提升星比對的比對時間。

3 結 束 語

本文將傳統的星比對與漸進比對相結合，提出了基于profile 比對的改進星比對算法，改進后的星比對算法顯著提高了比對的精度。為了減少比對時間，本研究還簡化了中心序列的選取，直接將最長序列作為中心序列。改進前后的算法時間復雜度是一致的，但實際時間不一定一致，改進的星比對算法運行時間要略大于傳統的星比對算法。同時，兩者運行時間隨著數據量級增大的增長速度是一致的。由此可見，本文提出的基于profile 比對的改進星比對算法不僅提高了比對的精度，又通過簡化中心序列的選取減少了星比對中選取中心序列的時間，同時也并未增加比對算法的時間復雜度。