以欠采樣速率實現盲譜感知及二維DOA 估計

張 展，魏 平，高 林，張花國

(電子科技大學信息與通信工程學院 成都 611731)

無線電頻譜資源匱乏，引入角度信息可以增加頻譜利用率[1]，這使得頻譜感知問題變為二維聯合譜(空間譜與頻譜)的感知問題。然而，以奈奎斯特率進行寬頻譜感知會帶來較大的數據處理壓力。利用欠采樣技術可以有效地降低采樣率，實現以低速率進行盲譜感知與波達方向(direction of arrival,DOA)估計。

基于欠采樣技術的譜感知與DOA 估計算法主要分為兩大類：基于多陪集采樣器的算法[2-6]和基于調制寬帶轉換器(modulated wideband coverter, MWC)的算法[7-9]。然而，上述算法解決的都是盲譜感知與一維DOA 估計的問題。文獻[10]在文獻[8]所提的L 形陣列的基礎上，提出了一個三維陣列。該陣列能拆分為兩個L 形陣列，并根據文獻[8]所提出的算法，提出了一種基于ESPRIT 技術的算法，實現以欠采樣速率進行頻率與二維DOA 的聯合估計。隨后，文獻[11]在文獻[4]所提算法的基礎上，在混合了多陪集與MWC結構的L 形陣列上，提出了一種能在欠采樣速率下進行頻率與二維DOA 聯合估計的算法。然而，目前這樣的算法有著復雜的硬件結構，且在低信噪比下性能受限。

本文提出了一種基于單通道MWC 的任意二維陣列的欠采樣接收機結構，基于該結構提出了兩種新的算法。這兩種算法能充分利用MWC 采樣器的特性[3]，在欠采樣條件下實現盲譜感知與二維DOA 估計。提出的接收機結構與算法能大幅度降低硬件資源的消耗以及復雜程度，并在低信噪比環境下，仍能保持較好的感知性能。

1 背 景

2 欠采樣陣列接收信號模型

2.1 單通道調制寬帶轉換器

MWC 結構的物理本質為：當接收信號um(t)在時域與周期信號p(t)相乘時，接收信號的模擬頻譜Um(f)會 以fp=1/Tp為間隔進行連續平移，且乘上對應的尺度因子。該尺度因子為周期信號的傅里葉級數系數。當通過低通濾波器后，會保留通帶范圍Fs內 的頻譜。該頻譜為 F 范圍內以fp為間隔的子頻帶譜與對應的尺度因子相乘后組合疊加的結果。

2.2 欠采樣接收機結構

圖1 單通道的調制寬帶轉換器

2.3 欠采樣的接收信號模型

3 盲譜感知及二維DOA 估計算法

3.1 基于張量秩一分解的盲感知算法

此時，已經實現了對信號源的盲譜感知及二維DOA 估計，將該方法命名為JSS-2DOA-CP 算法。

3.2 基于子空間分解的盲感知算法

4 仿真實驗

第一個仿真實驗驗證所提采樣接收機結構以及對應盲感知算法的有效性。該仿真設置了11 個50MHz 帶寬的復信號源。為了滿足文獻[9]中分析的系統參數選擇條件，二維陣列設置為包含M=9個天線的L 形陣列，即每個子陣列分別包含5 個陣元。信噪比SNR設置為 0 dB。圖2 描述了原始信號頻譜以及JSS-2DOA-CP 算法和JSS-2DOAMUSIC 算法重構的信號頻譜，并給出了其中一個信號源的重構頻譜放大圖。圖3 給出了信號源的三維參數的估計圖，圖中的3 個坐標軸分別代表方位角θ 、俯仰角α、載波頻率f。

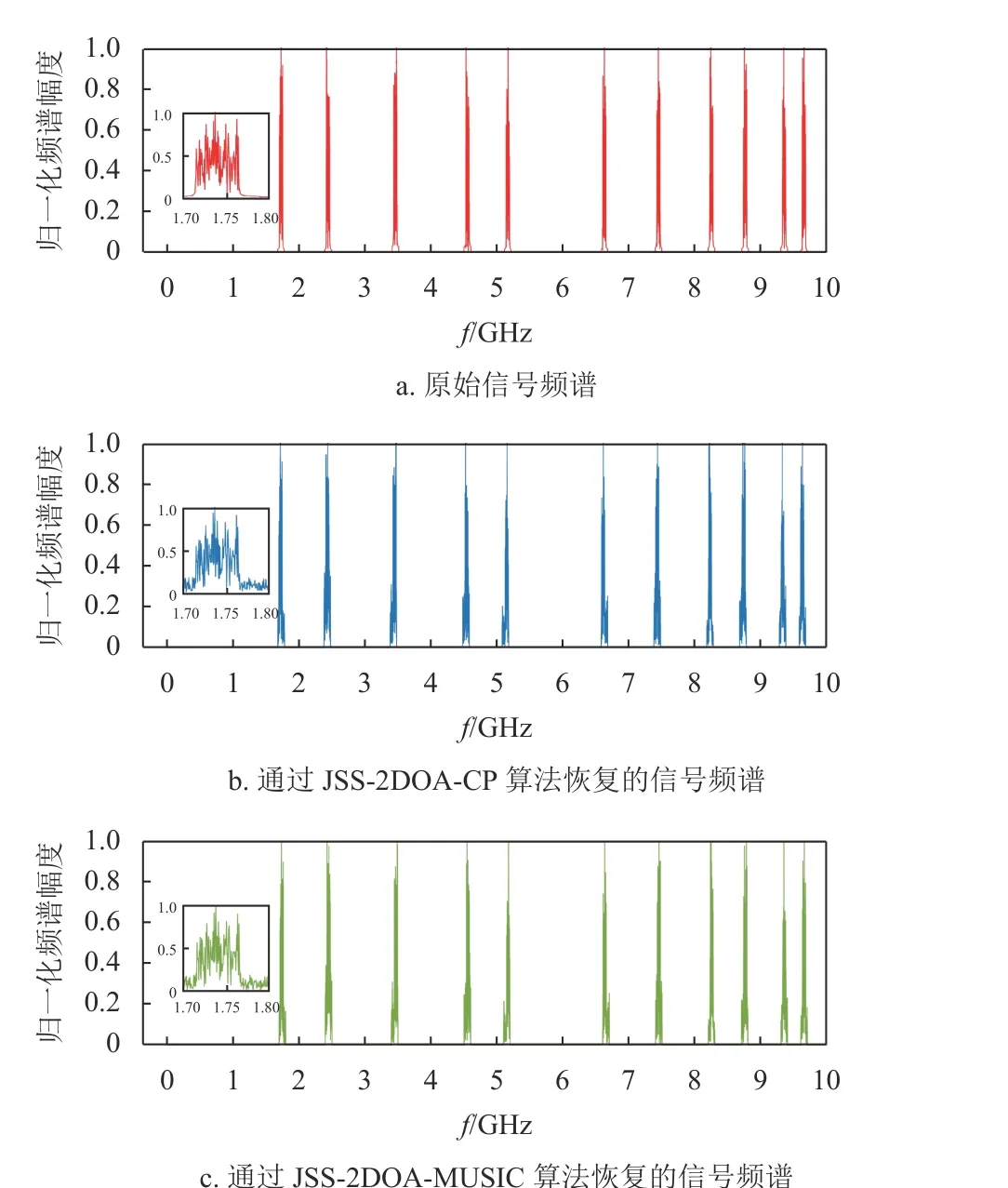
圖2 原始信號頻譜及重構的信號頻譜

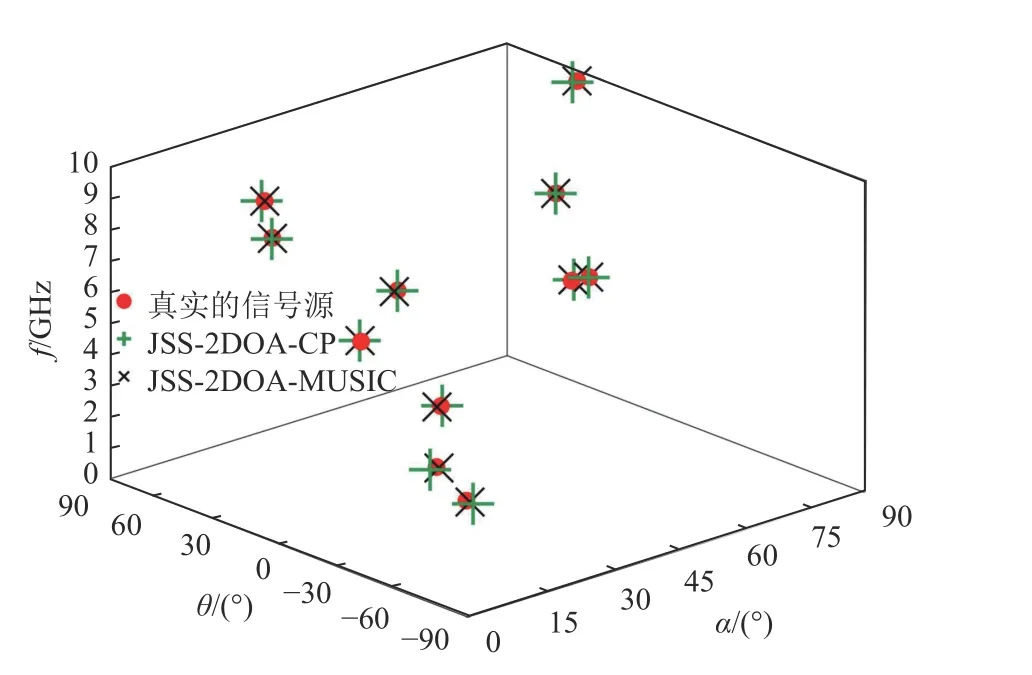
圖3 信號三維參數估計圖

從圖2～3 中可以看出，當系統設置滿足條件時，能夠完成對信號源所在子帶的正確估計，因而能夠估計得到信號的子帶頻譜，并由此重構出完整的信號譜。信號子帶頻譜的正確估計以及所在子帶位置的正確估計保證了載波頻率的高精度估計，因而對信號源的方位角和俯仰角也能正確估計。此外，仿真環境對應的奈奎斯特采樣率為1 0 GHz，而該系統用到了9 個天線，每個RF 電路的采樣率為400 MHz，因此系統總采樣率為3 .6 GHz，遠低于奈奎斯特率。該仿真也說明了所提出的采樣結構以及對應的算法能夠保證用以遠低于奈奎斯特率的總采樣率，在噪聲環境下，實現盲譜感知以及二維DOA 估計。

第二個實驗是為了驗證所提算法的性能，選擇了文獻[10]所提出的基于CaSCADE[8]的衍生算法和文獻[11]所提出的基于PABSS[4]的衍生算法作為本仿真實驗的對比算法。該仿真設置了兩個帶寬為50 MHz 的復信號源。所提的接收機結構是包含7個天線的L 形陣列，即M=7。為了保證公平性，即系統的總采樣率一致，設文獻[10]中算法對應的三維陣列，每個子陣列包含10 個天線，總計28 個天線；設文獻[11]所提的L 陣列，每個子陣包含15 個天線，總計29 個天線。因此，本文所提的系統總采樣率為2.8GHz，文獻[10]和文獻[11]算法的總采樣率分別為2 .8 GHz 和2 .9 GHz。仿真的信噪比SNR 變化范圍以3 dB 為間隔，設置為? 10 ～2 0 dB。圖4～6 分別表示了估計的載波頻率、俯仰角、方位角的RMSE 曲線。

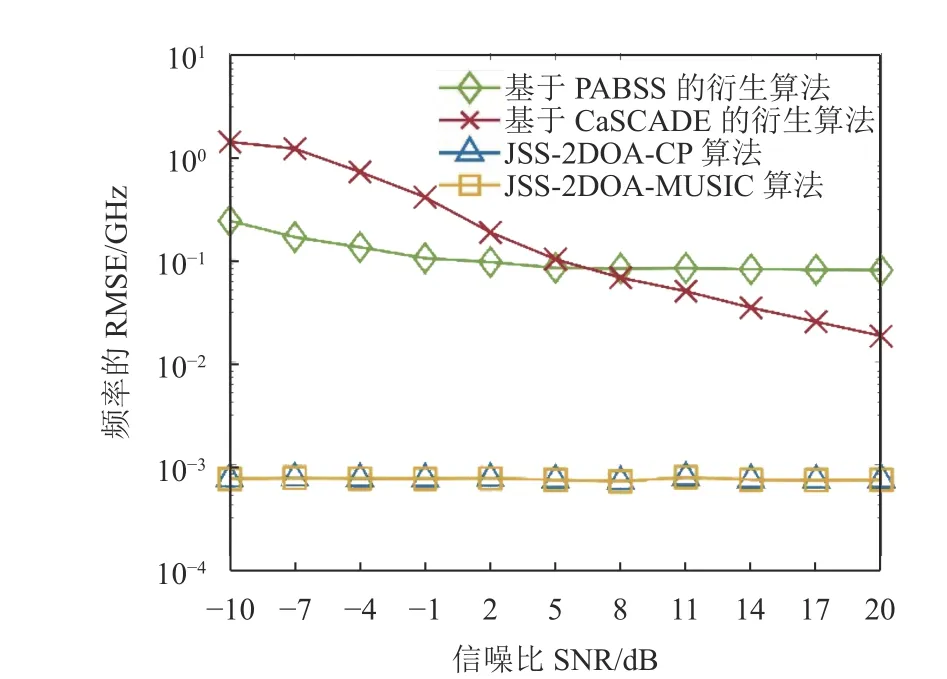
圖4 載波頻率的估計性能

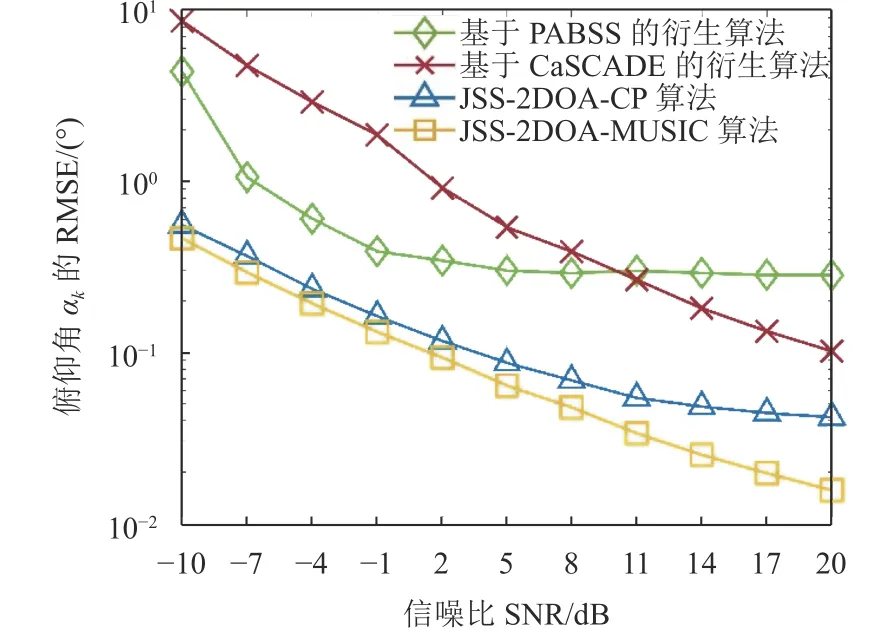
圖5 俯仰角的估計性能

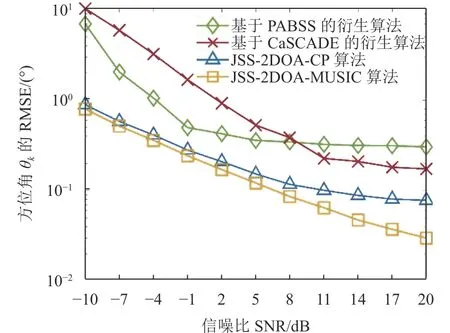
圖6 方位角的估計性能

從圖中可以看出，所提算法的性能相比于另外兩種算法，在譜重構以及頻率估計的性能上有著顯著優勢，這是因為本文算法的載波頻率估計依賴于對信號源所處子頻帶位置的估計，因此頻率的估計精度會大幅度提高，進而帶來譜重構的優勢。此外，方位角和俯仰角的估計性能在低信噪比情況下也有顯著優勢。不僅如此，相比于對比算法的系統設計，本文所提出的系統結構有更少的硬件資源開銷，因此本文所提的接收機結構以及對應的盲感知算法，能在降低資源開銷的同時仍保證感知性能的魯棒性。

5 結 束 語

本文提出的基于壓縮采樣的盲譜感知及二維DOA 估計算法，充分利用了MWC 中的周期信號產生對應的傅里葉級數系數矩陣，通過估計出信號源頻譜所處的子帶位置，以此提高載波頻率的估計性能，進而使得在低信噪比環境下，信號源的方位角和俯仰角的估計精度大幅度提高。這種區別于傳統的利用空間相位信息估計載頻與二維度DOA 的思路，大幅度提高了感知性能以及估計的魯棒性。此外，設計的接收機系統以及對應的感知算法能有效降低系統硬件資源的開銷，對認知無線電中多維聯合譜感知問題具有重要意義。