時間序列數據挖掘中的聚類研究綜述

李海林，張麗萍

(1. 華僑大學信息管理與信息系統系 福建 泉州 362021；2. 華僑大學應用統計與大數據研究中心 福建 廈門 361021)

大數據背景下，數據挖掘與分析成為信息處理和知識管理等相關學科領域重點關注的研究對象[1]。在各種復雜數據類型中，廣泛存在于金融市場和工業工程等領域的時間序列是一種與時間密切相關的數據，根據變量屬性維度的大小其可分為單變量和多變量兩種時間序列。相應地，時間序列數據挖掘是從時間序列數據庫中發現信息與知識的理論與方法，為幫助政府和企業管理者在相關領域中提供更為可靠的輔助決策與技術支持[2]。時間序列的高維性具有時間維度長、屬性變量多、數據體量大等特征，給傳統數據挖掘技術的實施帶來了極大困擾，在一定程度上阻礙了其在時間序列數據分析領域中的應用與發展。因此，運用數據挖掘技術從高維時間序列數據中發現信息和知識成為了數據分析領域中具有挑戰性且最主要的研究方向之一[3]。

傳統時間序列數據分析主要基于某種數據分布假設，再選取和制定計量經濟模型來對時間序列數據預測分析。在大數據時代，除了需要傳統的統計模型對時間序列數據進行預測與分析之外，鑒于時間序列數據具有時間維度長、屬性變量多和數據體量大等高維性特征，借助機器學習、模式識別、智能計算和數據挖掘等模型和算法對高維時間序列數據可以進行深入研究與挖掘。聚類是數據挖掘相關研究和應用中非常重要的方法，涉及計算機科學、模式識別、人工智能和機器學習等多個研究領域，同時也常被用于教育、營銷、醫學和生物信息學等學科，在大數據、人工智能和機器人等熱點領域有突出貢獻[4]。如在大規模群體決策中，聚類分析被用于劃分大規模群體、處理非合作行為和社區發現等[5-6]。聚類分析也是一項重要而且基礎的工作，其過程包括了時間序列的數據表達、特征提取、相似性度量以及具體聚類模型與算法等。為此，本文對時間數據挖掘中的聚類分析進行綜述研究，首先介紹了目前時間序列聚類方法分類，然后分別從特征表示、相似性度量、聚類算法和簇原型等方面進行國內外研究狀況分析，最后分析了目前研究存在的不足，同時給出了未來的研究方向。

1 時間序列聚類

時間序列聚類研究大體上可分為3 種類型[7]，分別為整體時間序列聚類、子序列聚類和時間點聚類。整體時間序列聚類把每條時間序列視為數據對象，對具有共同數據特征的時間序列對象進行聚類。它常以相似性度量為基礎，結合數據降維和特征表示來找出兩個數據對象之間的共性，進而實現時間序列數據的簇劃分。

如圖1 所示，分別使用主成分分析(principal component analysis, PCA)和 對 稱 性 主 成 分 分 析(asynchronism-based principal component analysis,APCA)[8]對10 條Synthetic_Control 時間序列數據進行特征表示，并使用相應的相似性度量方法結合層次聚類實現整體時間序列的聚類分析。

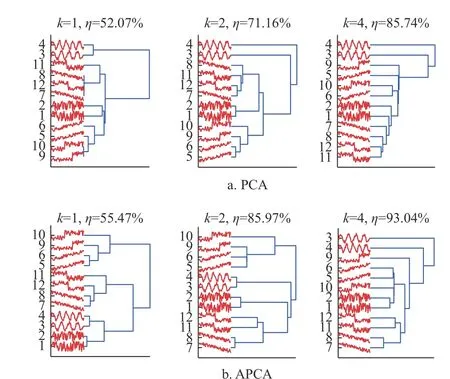
圖1 兩種方法對整體時間序列數據層次聚類

子序列聚類通常指對一條時間較長的一元序列利用滑動窗和矢量量化等方法進行子序列劃分，并使用相應聚類方法實現分段子序列的聚類。子序列聚類方法可以有效地發現較長時間序列中的頻繁模式和異常片段，也能夠發現不同時間序列數據之間存在的共同模式和關聯關系。

時間點聚類則是從時間點和相應數據點兩個角度出發來研究基于時間點的數據對象之間的近似性，把具有較高相似性的時間點聚合成同一簇，進而實現時間序列數據點劃分[7-8]。該方法能夠用來對一條時間序列進行分段劃分，實現數據降維和特征表示，與傳統時間序列分割表示方法相比，具有較高的時間效率。

目前國內外學者對于子序列聚類的研究目前尚存一些爭議[9]。鑒于整體時間序列聚類的模型與算法可直接或間接應用于子序列聚類和時間點聚類，大部分集中于對整體時間序列聚類的研究。主要研究方法有：1) 傳統聚類方法，如K-Means、模糊聚類和基于密度的等聚類方法，根據時間序列的數據特征定制合適的距離度量函數，實現原始時間序列數據聚類[10]；2) 對時間序列數據通過特征空間轉化[11]，將原始時間序列數據轉化為另一特征空間的數據對象，再選取合適的傳統聚類方法在特征空間中對數據對象進行聚類[12]；3) 通過時間序列數據的多分辨率解析，在不同分辨率視角下結合不同方法進行聚類分析，提升傳統方法的聚類效果[13]。

2 國內外研究現狀

針對時間序列數據挖掘中的聚類分析主要集中在整體時間序列的聚類研究，通常整體時序數據聚類方法也可用于子序列聚類中，使得整體時間序列聚類顯得更為重要。由于時間的連續性，對時間點聚類的研究相對較少。

如圖2 所示，重點從整體時間序列聚類的視角來分析時間序列數據挖掘領域中的聚類研究狀況。有關整體時間序列聚類的國內外相關文獻主要從4 個方向對其進行了相關理論和方法的研究，分別為數據降維與特征表示、相似性度量、聚類模型與算法和簇原型，采用不同的技術手段和理論方法從這4 個方向進行分析與探究。

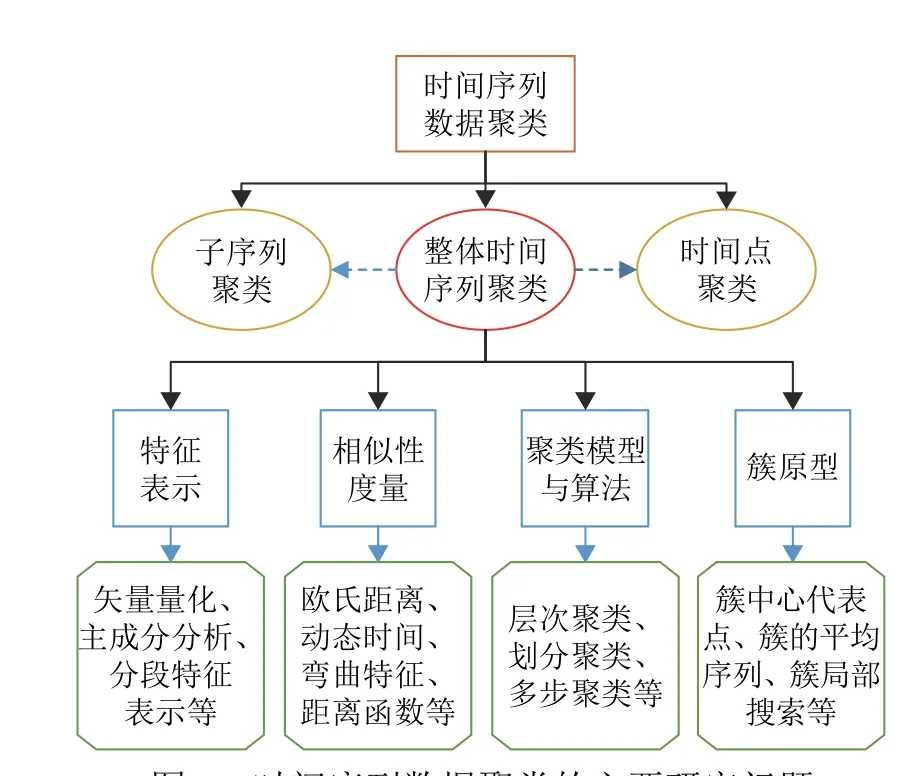
圖2 時間序列數據聚類的主要研究問題

2.1 研究地位

目前已經出現了不少成熟經典的聚類模型與算法，但一些基本問題始終是該領域的研究重點，其中包括不同結構特征數據的相似性度量、高維數據的降維與特征表示、基于噪聲數據的聚類魯棒性、大規模數據集聚類算法的有效性選擇等[14]。高維時間序列數據與傳統數據不同，隨著時間維度的增加，各時間點產生的數據具有不確定性[15]，在聚類分析過程中除了要解決因高維性給有關模型和算法帶來精度不高和復雜度過大等問題，還需要考慮動態實時、不確定性和高噪聲等其他特征因素給聚類結果帶來的影響。另外，時間序列聚類結果所產生的模式通常也被用于其他時間序列挖掘任務和方法中，如時間序列的數據降維與特征表示、模式匹配、關聯分析、分類、數據可視化等[16-18]，使得整個時間序列數據挖掘任務具有更為出色的效果。

時間序列數據挖掘包括特征表示、相似性度量、聚類、分類、關聯規則、模式發現和可視化等重要任務和關鍵技術[2]。聚類分析與特征表示和相似性度量方法一樣，通常作為其他時間序列挖掘任務的子程序或中間件，以便更好地提升相關挖掘技術的性能和質量[10]。時間序列聚類分析研究的另一個重要動力來自于實際應用領域中超大容量數據的獲取，包括經濟金融、電子信息、醫療行業、航空航天、天體氣象等。這些與時間相關的高維數據隱藏著大量有價值的信息和知識，需要通過聚類分析對時間序列數據進行模式發現，進而有針對性地對相關模式和知識進行處理，以便數據科學家和管理者進行技術分析和決策支持。

由于時間序列數據自身存在一定的特殊性，使得數據降維與特征表示以及相似性度量方法成為其他時間序列數據挖掘方法研究的基礎任務，其質量好壞在一定程度上影響其他挖掘任務的效果[19]。文獻[20]對單變量和多變量兩種時間序列數據的特征表示和相似性度量進行了較為系統的研究，研究成果能較好地改善和提高有關挖掘技術和方法的質量和效率。同時，聚類自身也可用來發現時間序列中的頻繁模式或時間序列數據庫中的奇異模式，甚至作為一種降維手段來實現數據特征表示[21]。另外，在大部分情況下，時間序列聚類通常是建立在特征表示和相似性度量基礎之上的一種機器學習方法，實現獲得較高質量的聚類分析結果[10]。

2.2 數據降維與特征表示

數據降維和特征表示是高維時間序列數據挖掘中至關重要的過程，其目的是對高維數據進行數據變換，在低維空間下使用相應的特征來表示原始時間序列的關鍵信息，進而提高時間序列聚類算法的效率和質量。目前，已有一些較為成熟的方法對一元時間序列進行特征表示，包括矢量量化[22]、分段表示[23]、聚合符號化表示[24]、多項式回歸參數[25]和模型參數[26]等。鑒于多元時間序列數據的廣泛性和重要性，主要從序列的時間和屬性兩個維度進行數據降維，代表性方法有基于主成分分析的[27]、基于獨立成成分的[12]、基于奇異值分解的[28]等。

將時間序列數據轉化為復雜網絡方法，再使用復雜網絡的拓撲結構特征來表示原始時間序列數據也是目前較為常用的一種時間序列數據特征表示方法，通常包括基于可視圖、基于相空間重構法、基于遞歸法和基于符號模式等建網方法[29]。特別地，可視圖可以將周期時間序列、隨機時間序列和分形時間序列分別轉化為規則網絡、隨機網絡和無標度網，其拓撲結構能夠較好地反映時間序列的數據特征。若時間序列中兩個數據所表示的直方條能夠畫一條不與任何中間直方條相交的直線，則此直方條組所對應的數據組之間可以形成網絡連邊，即：

基于數據降維和特征表示的時間序列聚類主要從基于形態的、基于特征的和基于模式的等方面來研究。基于形態的時間序列聚類[30]主要從數據形態變化的角度來匹配序列之間的相似性，包括同步形態和異步形態，進而聚類算法可將具有相似性形態變化特征的時序對象歸入同一簇。基于特征的時間序列聚類[31]將時間序列進行數據轉化，在低維的特征空間中進行時間序列的聚類分析。基于模式的時間序列聚類[10]則是將原始時間序列轉化為模型參數，結合傳統聚類算法實現時間序列的模式識別。

2.3 相似性度量

相似性度量也是時間序列聚類算法中必不可少的中間件，基于相似性度量的聚類算法有時間序列數據劃分聚類、層次聚類和基于密度的聚類等。文獻[32]提出了時間序列相似性搜索過程中距離度量的理論基礎，要求設計的快速近似度量函數滿足真實距離的下界性，以免相似性檢索時發生漏報情況。

目前存在各種不同的時間序列距離度量方法[19]，最典型的兩種方法為歐氏距離(Euclidean distance,ED)和動態時間彎曲方法(dynamic time warping,DTW)[11,33-34]。歐氏距離通常要求兩條時間序列具有相等的長度，即對于兩條時間序列A與B，有：

如圖3 所示，歐氏距離對時間序列進行了同步硬性度量，動態時間彎曲方法根據最優化匹配路徑，實現異步相似形態的度量。前者滿足三角不等式，比較適用于時間序列的相似性搜索，但其結果易受異常數據點的影響，且無法度量不等長時間序列之間的相似性；后者利用動態規劃方法從兩條時間序列中找到一條距離最優的彎曲路徑，使具有相似形態的異步數據相互匹配，進而實現不等長時間序列之間的距離度量，但其平方階的時間復雜度限制了其在高維時間序列數據聚類過程中的應用。

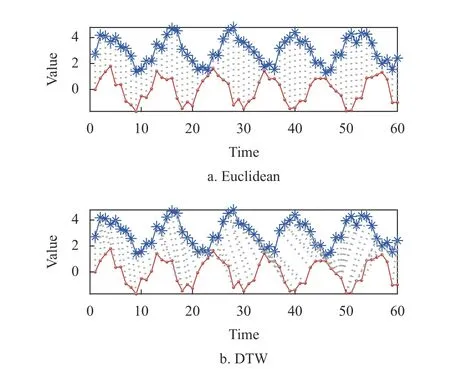
圖3 歐氏距離與動態時間彎曲度量

大量實驗表明，在時間序列數據聚類中，使用SBD 可以獲得比使用DTW 更好的聚類性能和效果。

另外，一些基于特征表示的距離度量方法也常用于時間序列的聚類分析，如基于多項式參數的[25]和基于主成分分析的[27]等距離度量方法在時間序列數據挖掘中起到了提升聚類效果的作用。

2.4 聚類算法

時間序列數據聚類主要包括層次聚類、劃分聚類、基于模型的聚類、基于密度的聚類、基于格的聚類和多步聚類等[18]。時間序列層次聚類[36]是一種具有直觀效果的聚類方法，分為基于凝聚和基于分裂的層次聚類。特別地，為了檢索特征表示或相似性度量方法的有效性，通常被用來直觀顯示基于形態的或基于特征的時間序列聚類情況。

劃分聚類[37]是時間序列聚類算法研究中最為常用的方法之一，通常借助于相似性度量函數來實現簇劃分，具體方法包括K-Means、K-Medoids和 FCM。例如，在時間序列SBD 距離計算中，使用K-Means 的思想來對時間序列進行快速有效地聚類，通過尋找最優參數來達到目標評價函數最優，即：

基于劃分的聚類方法需要事先設定聚類個數，但在應用中通常無法確定聚類個數，特別是對海量高維時間序列數據來說，該參數的確定顯得更加困難。文獻[38]研究了適當的初始中心對時間序列K-Means 聚類的質量和效率有很大影響。文獻[39]認為K-Means 和K-Medoids 與層次聚類相比，其具有較好的時間性能，比較適用于時間序列的聚類分析。與這兩種聚類相比，FCM 是一種基于模糊理論的軟劃分，該方法在一定程度上考慮了時間序列數據對象的不確定性問題[40]。

基于模型的聚類與其他方法不同，它假設同一簇中數據服從某種模型的數據分布，通過數據模型學習來試圖調整近似模型，使其接近數據客觀存在的真實模型[41]。目前也有一些較為成熟的方法[10]，如自組織映射、多項式回歸分析、高斯混合模型、ARIMA 模型、馬爾可夫鏈和隱馬爾可夫模型等。然而，基于模型的聚類方法存在一些問題有待研究：一方面，模型需要用戶事先設定假設模型和模型參數，若假設模型與真實模型相差甚遠，則會導致最終的聚類結果不準確；另一方面，此類模型需要較長的計算時間，不利于高維時間序列數據和動態時間相關數據的聚類分析。

基于密度的和基于格的聚類方法[42-43]先將時間序列數據轉化為另一種數據形態，使其能夠適用于傳統數據挖掘中的聚類算法，如DBSCAN、OPTICS、STING 和Wave Cluster 等方法。多步聚類方法[44]則是從聚類算法設計和分析的角度出發，通過多種方法對時間序列數據進行分步聚類，其效果通常要優于傳統基于特征表示的、基于相似性度量的和基于模型的聚類方法。

數據挖掘中的聚類算法[4]較為成熟，除了具有較為完善的理論基礎，其在許多領域都有很好的應用效果，因此，它們也可以直接或間接應用于時間序列數據的聚類分析。然而，由于時間序列數據具有時間和變量高維性、概念漂移、隨機性和混沌現象等特點[29,45]，需要進行數據降維、特征表示和相似性度量，也包括異常點發現等前期處理工作。根據傳統聚類算法思路設計適用于時間序列數據聚類的模型和算法，如將傳統聚類思路結合復雜網絡特征，實現多變量時間序列數據的聚類[46-47]。

2.5 簇原型

簇原型[48]是指某一特定簇的近似代表對象，其質量好壞直接影響某些聚類算法的分類效果，如K均值、模糊聚類和近鄰傳播聚類(AP)等算法都需要定義相應的簇原型。在時間序列數據聚類領域中，簇原型大體可分為3 種，分別是簇中心代表點[49]、簇的平均序列[50]和基于局部搜索的簇原型[37]。

通過基于DTW 的距離計算來重復交替迭代計算簇中心序列和分配簇成員，實現時間序列數據的聚類。

如圖4 所示，圖4a 顯示了同一個簇中3 條時間序列樣本的形態波動示例，圖4b 中較粗曲線表示了DBA 方法的簇平均序列，易發現基于DBA的簇平均序列的形態波動與簇成員的形態波動相似。基于局部搜索的簇原型[37]是一種在簇類中進行局部搜索找出簇原型的方法，與基于簇中心代表點的和基于簇平均序列的K中心點聚類算法相比，基于局部搜索簇原型的K中心聚類具有較好的挖掘效果。

圖4 簇平均代表序列

2.6 應用研究

時間序列數據挖掘中的聚類研究成果主要應用于兩個方面：1)將聚類算法作為其他時間序列數據挖掘技術和方法的子程序或中間件，其聚類結果可以輔助其他數據分析任務的順利進行并提高數據挖掘任務的效果[51-52]；2)聚類算法可被運用在具體的實際生產和生活領域中，如生物信息、天體氣象、經濟金融、醫療衛生、語音識別和工業工程等[53-57]，根據具體背景知識來發現相關行業時間序列數據中的興趣模式、異常模式和頻繁模式。

在工業工程領域中，文獻[58]提出了一種基于灰色關聯聚類的特征提取算法，利用灰色關聯度作為動態聚類歐氏距離的思想，構建以某型渦扇發動機為例的灰色關聯聚類特征提取模型，以便滿足故障診斷要求。特別地，在金融數據分析應用領域中，通過時間序列聚類分析方法可以發現股票市場中相似的股票群，結合滑窗法可以實現基于動態衍化聚類的股票識別。金融市場被眾多因素共同影響，不僅有宏觀的政治、經濟等環境因素，還有微觀的企業運作方式、人們的心理作用等因素。通過對金融時間序列進行聚類，可以挖掘出金融市場的內在機制，對揭示數據背后的發展變化規律有重要作用。文獻[59]提出一種基于影響力計算模型的股票網絡中心節點層次聚類算法，利用社區發現方法對股票時間序列進行聚類。文獻[60]提出一種基于支持向量回歸和自組織神經網絡的聚類方法，提取投資組合選擇方法，實現了金融股票價格和波動率的預測分析，對印度國家證券交易所102 支股票進行最優投資組合，具有低風險高盈利的特征。文獻[61]針對金融股價時間序列數據的時間屬性變量高維性，提出利用三階段聚類模型，對股票進行增量式聚類，進而發現上市公司之間的聯動關系。

3 主要問題與未來研究方向

時間序列數據聚類研究主要集中于整體序列數據對象，在數據降維與特征表示、相似性度量、聚類模型與算法、簇原型和應用等方法上取得了一定的學術進展，擁有應用價值，但仍存在一些問題有待探討，以便系統性地研究和提高聚類分析在時間序列數據資料中的挖掘質量和應用性能。

1) 傳統時間序列聚類模型與算法主要以一元時間序列數據為研究對象，通過數據轉換、特征表示或模型參數實現時間維度的降維，利用數據挖掘中經典聚類方法進行分析，缺少兼顧時間序列數據時間維度長、屬性變量多和數據體量大等高維性的問題。特別地，數據體量大造成算法在運行期間需要消耗巨大的內存空間，使得以靜態處理方式為基礎的傳統聚類算法在此類高維時間序列數據集中無法得到有效地運行。因此，根據高維時間序列數據自身的特點，需要研究適用于高維時間序列數據的實時、動態或者增量運行的聚類算法。

2) 基于原始數據的時間序列距離度量通常需要較大的時間復雜度和空間復雜度，并且大部分距離度量方法對數據中的扭曲數據較為敏感，使其在計算過程中無法獲得直觀的度量效果。數據降維后的特征表示在一定程度上能夠改善此種境況，降低了聚類算法和模型的復雜性，但特征表示對高維原始時間序列數據的精確定位難以實現，最終影響聚類模型與算法的精度。針對基于特征表示和相似性度量方法的高維時間序列數據聚類模型與算法研究，需要改變傳統方法僅對高維數據進行某個特定維度上的數據降維和特征表示，制定適用于特征表示后由于信息丟失而造成距離度量不準確的情況，進而提升相關模型與算法的聚類效果。

3) 動態時間彎曲是時間序列數據挖掘領域中最為常用的相似性度量方法，它能有效地匹配時間序列數據中的近似形態趨勢，對時間點異常數據不敏感，能夠度量不等長時間序列之間的相似性，具有較好的度量質量和較高的準確性等優勢。在高維時間序列數據庫中，過長的時間維度、過多的屬性變量和過大的數據體量造成動態時間彎曲方法容易平滑時間序列局部形態的特點，不能有效反映高維時間序列數據對象之間的形態變化關系，無法實現真實距離的有效度量，進而影響基于動態時間彎曲的高維時間序列聚類效果。如何提高動態時間彎曲方法的精確度量和計算性能是高維時間序列聚類研究中需要解決的問題之一。

4) 關于時間序列聚類的研究目前大多數集中在提升特征表示、距離度量和簇原型的質量或效率上，對于聚類本身的設計與研究相對不足。雖然已有學者利用多步聚類方法在一定程度上改進了傳統聚類算法在時間序列數據中的分析效果，但也存在步驟繁瑣、聚類結果易受參數設置影響、計算性能較低等問題。同時，由于時間序列數據高維性和其他特征因素的影響，聚類方法在相關應用中大多數局限于變量屬性少、時間維度短和數據量少等對象的分析，較少考慮不確定性和高噪聲等因素的影響，使得聚類分析理論和方法在實際應用中具有局限性。為此，通過總結現有的時間序列聚類算法優缺點，結合具體問題中的數據特征，在考慮多種特征因素影響的情況下來構建符合高維時間序列數據的高性能聚類算法值得深入研究。

4 結 束 語

本文梳理了目前常用的時序聚類算法，綜述了該領域中的相關研究成果，歸納了已有研究存在的不足，提出了一些值得研究的方向。研究發現，時間序列數據挖掘中聚類模型與算法的研究順應了大數據時代潮流，解決了高維性給傳統時間序列聚類分析帶來不能快速有效挖掘的問題，提高和拓展了時間序列數據挖掘領域中的相關理論和方法。時間序列數據聚類研究成果能給政府部門和企業對相關事務決策提供更為完備成熟的理論基礎與技術，以便進行更為科學合理的智能管理。