基于深度學習的印花織物循環圖案基元分割

林 峰，向 忠

(浙江理工大學 機械與自動控制學院，浙江 杭州 310018)

0 引 言

目前印花廠在制作印花圖樣時，一般由設計師將樣布中的循環圖案基元分割出來，繪制成合適的模板，最終根據實際需要排列成各式各樣的印花圖樣。這種成本極其高昂，耗時較長，極大地增加了印花織物開發設計的時間。面對快速發展的企業需要，亟需開發一種自動分割織物循環圖案基元的方法。近年來，隨著深度學習技術的發展，為業界提供了一條新的思路。

傳統的分割算法主要可以分為三類，一類是基于空間域的方法，一類是基于頻域的方法，一類是基于顏色域的方法。第一類方法是利用圖像函數局部峰值之間的距離確定循環圖案的周期規律，并由此得到織物循環圖案基元。最早Terzopoulos等人利用灰度共生矩陣(gray-level co-occurrence matrix，GLCM)尋找出循環基元的周期規律[1]，但是該方法進行周期分析耗費的計算時間很長，并且穩定性較差。為此，Parkkinen等人利用GLCM的統計量K進行計算，在一定程度上提高了GLCM方法的計算速度[2]。Lin等人嘗試使用自相關函數進行峰值計算[3]，這種方法對局部畸變有一定容忍度，然而這種方法需要對自相關函數進行平滑處理，因此計算時間同樣比較長。景軍鋒等人提出一種使用距離匹配函數(distance matching function，DMF)進行循環圖案基元分割的方法[4-5]，這種方法的優點在于計算時間比較短，然而使用距離匹配函數的方法對幾何畸變等噪聲非常敏感。Unser等人提出了和差直方圖(sum and difference histograms，SDH)的方法[6]，該方法的分割效果不弱于基于GLCM的方法，大大提高了計算速度，但是缺點在于只能對灰度圖進行處理，因此會丟失很多顏色信息。為此Li等人提出了利用HSV顏色空間的H分量進行計算的方法[7]，一定程度上提升了分割效果，但是該方法無法處理包含多種花型的圖案基元的復雜印花織物。何旋等人提出一種基于自適應模板匹配的方法，該方法以邊緣點密度為評價標準確定出模板，只適用于簡單印花織物，對于包含多種花型的圖案基元的復雜印花織物，由于循環圖案基元之間的間距很小，該法依然難以分割[8]。

第二類方法是基于頻域的方法[9-10]。Matsuyama等人采用傅里葉變換進行周期分析[11]，循環圖案基元的周期可以通過傅里葉函數頻譜圖的脈沖分布來確定，但是該方法只適用于純色織物。

第三類方法是基于顏色域的方法。Kuo等人提出利用顏色特征對印花織物循環圖案基于進行分割[12]，首先由彩色掃描儀獲得彩色的印花織物圖案，采用模糊均值聚類方法獲得圖案的顏色特征，印花織物循環圖案基元經過霍夫變換得到，然而這種方法只適用于顏色邊界比較清晰的圖案，對顏色豐富且復雜的圖案基元無法有效分割。

上述的分割方法往往需要人工設計一個特征提取器，適應性較差，只對一些簡單的循環圖案基元有效，無法適應具有多種花型的循環基元的復雜印花織物圖案，不能滿足實際的需要。近年來，深度學習算法的應用日趨廣泛，推動了計算機視覺的快速發展，特別是在圖像分類[13-15]、目標檢測[16-17]、實例分割[18-19]等方面。類似的，在紡織領域，深度學習的方法被應用于織物瑕疵檢測方面[20-21]，并且已經取得了顯著的檢測效果，但是如今幾乎沒有學者將其應用在織物循環圖案基元分割上。為此，該文提出了一種基于預訓練卷積神經網絡的分割方法。實驗結果表明，該文算法不僅可以分割具有簡單花型的織物循環圖案基元，還可以準確分割包含多種花型的織物循環圖案基元，具有較好的魯棒性。

1 循環圖案基元分割算法

1.1 算法流程

該文算法利用預訓練AlexNet網絡進行特征提取，然后對特征進一步計算，分割出織物循環圖案基元。

該文算法先將織物圖像輸入到預訓練AlexNet網絡中進行特征提取，之后對每張特征圖在霍夫空間中進行投票，得到循環基元的尺寸，最后在輸入圖像中分割出織物循環基元，算法流程如圖1所示。

圖1 算法流程

1.2 預訓練AlexNet網絡

Alex Krizhevsky等人提出了AlexNet網絡[22]，并在當年的圖像分類比賽中一舉奪魁，獲得了廣泛的關注。隨著卷積神經網絡變深，會產生梯度消失的問題。為此，與以往的卷積神經網絡相比，所提出的網絡中應用了ReLU激活函數進行處理，取得了很好的效果，同時使用了局部響應歸一化，大幅度提升了模型的泛化能力。此外，該網絡還在全連接層中添加Dropout層，對全連接層的輸出特征隨機進行舍棄，解決過擬合問題。AlexNet的網絡結構如圖2所示。

圖2 AlexNet網絡結構

該網絡一共有5個卷積層，卷積層通過卷積運算實現特征提取，每一個卷積層的輸出進行ReLU激活，然后使用最大值池化后的輸出作為下一個卷積層的輸入。第5個卷積層經過池化后連接了3個全連接層，得到1 000個輸出值，這1 000個輸出值分別對應類別的概率。該文采用經過預訓練的AlexNet網絡進行特征提取，移除網絡的全連接層，只留下卷積層。由于去掉了全連接層，輸入的織物圖像可以任意大小，這使得網絡可以更好地適應實際場景。

1.3 循環基元尺寸計算

如圖3所示，依次分別為AlexNet預訓練網絡的第1到第5個卷積層，卷積神經網絡第一層通常學習邊緣和其他低層次特征。隨后，隨著層數變深，網絡可以學習到更深層的特征表示，比如復雜的顏色和花型。因此，卷積神經網絡可以被認為是一組具有不同抽象層次的過濾器，當圖像區域出現特定特征時，這些過濾器就會被激活。該文使用這些過濾器作為特征提取器，無需任何人類的先驗知識，就可以自主學習到復雜的特征。

圖3 AlexNet網絡的卷積層

圖4 特征層中的激活峰值

帶有循環圖案基元的印花織物具有循環往復的特點，將織物圖像輸入預訓練網絡后，在不同特征層間會產生有規律的激活峰值，該文使用非極大值抑制算法獲得這些峰值，特征層中的激活峰值如圖4所示。每對峰值對應一組位移向量。因此，不同特征層中出現次數最多的位移向量的絕對值，就是循環圖案基元的尺寸。該文在霍夫空間中對每一對位移向量進行投票，來確定循環圖案基元的尺寸。

如前所述，該文使用的預訓練網絡一共有5個卷積層，l表示在第l個卷積層，其中l∈L。f表示特征層，fl∈Fl表示卷積層中所有的特征層。每個特征層中激活峰值的位置用p表示，則有pm,pn∈Pfl。由每對激活峰值得到一組位移向量，用sm,n表示。位移向量的計算公式如式(1)所示。

通過對2組患者實施不同的治療措施，2組患者病情均出現不同程度的好轉，但是觀察組患者治療有效率97.1%顯著高于對照組患者62.9%，差異有統計學意義（P<0.05）。 見表 1。

Sfl={sm,n:|pm-pn|,m≠n}

(1)

其中，|. |是向量的絕對值。

接下來需要從位移向量集合Sfl按照出現次數，將出現次數最多的位移向量作為循環基元的尺寸。在這一步將Sfl映射到霍夫空間H中進行投票。由于每個卷積層中的特征層大小不同，投票無法直接進行，需要進行權重歸一化。該文假設每個投票服從以sm,n為中心的二維正態分布，σl為第l個卷積層的協方差矩陣，計算過程如式(2)所示：

(2)

其中，

(3)

由此，循環基元尺寸的計算公式如下：

(4)

1.4 循環圖案基元分割

在得到循環圖案基元的尺寸后，需要進一步在織物圖像中分割出完整的基元。為此，先對特征層進行挑選，減少計算量。根據特征層擁有的位移向量數量|Sfl|，對特征層賦予權重wfl，權重計算公式為：

(5)

其中，γ是先驗值，該文將其設置為0.8，β為鄰域半徑。

(6)

然而利用M(x,y)進行簡化會產生一定的偏移，該文將偏移量記為o*=(ox,oy)，偏移量的計算公式為：

隨后利用IPM算法[23]在優化后的特征層的位移向量空間中進行計算，得到循環圖案基元的質心坐標，最后用質心坐標和前面確定的循環基元尺寸分割出最終的循環圖案基元。

2 實驗結果

本次實驗使用Pytorch深度學習框架中的預訓練AlexNet網絡模型進行。實驗運行在Centos7.0系統下，服務器配置為1張英偉達GTX 1080Ti顯卡，64G運行內存及512G的固態硬盤。

為更好地分析該文算法的性能，與其他算法進行了對比，以驗證算法的優越性。目前關于印花織物循環圖案基元最新的算法是Li等人提出的HSDH算法[7]。HSDH算法首先將RGB彩色圖像轉為HSV顏色空間中的圖像，然后提取出圖像的H分量，進行去噪和直方圖均衡化處理。隨后利用這個分量的圖像代替以往研究者采用的灰度圖像，分別計算水平方向和垂直方向的和差直方圖的能量特征函數，根據能量特征函數的峰值間隔得到織物圖案的周期，從而分割出印花織物的循環圖案基元。

圖5 簡單織物分割結果

在實際生產中，為了滿足消費者的需求，企業生產的印花織物通常具有豐富的紋理特征，每一個循環圖案基元中包含多種花型，形成了不同風格的織物圖案，因此能夠識別出具有多種花型循環圖案基元的復雜印花織物具有重要的意義。循環圖案基元包含的花型越多，擁有的特征越復雜，分割的難度也就越大。該文首先在簡單的印花織物圖像上進行實驗，這種織物的循環圖案基元中只包含少量花型，一般為1～3種，特征較為簡單。實驗結果如圖5所示，左列為HSDH算法的分割結果，右列為該文算法的分割結果。從圖中可以看出，該文算法與對比算法都能分割出完整的織物循環圖案基元。

隨后該文在復雜的印花織物圖像上進行了實驗，這類織物的循環圖案基元包含多個花型，一般為4種以上，特征較為復雜，連人眼也無法快速地分出它們的循環圖案基元。所有的實驗結果如圖6所示。結果表明，在這類復雜的印花織物上，HSDH算法幾乎不能分割出完整的循環圖案基元，在能量函數曲線上是一條直線。而該文算法依然可以準確地分割出完整的循環圖案基元。這是因為在卷積神經網絡中，淺層通常可以獲得邊緣等低級特征，而深層可以學習到更復雜的特征信息，例如復雜形狀，使得該文算法對復雜印花織物的循環圖案基元也具有很好的分割效果。

圖6 復雜織物分割結果

該文進一步對兩種算法的效果進行了定量評價，以驗證算法的可行性，其中簡單織物和復雜織物圖像各18張。該文算法與HSDH算法的準確率如表1所示。從表中可以看出，對于簡單織物，該文算法的準確率比HSDH算法高出11.1%，在復雜織物上更是高出77.8%。得益于卷積神經網絡強大的特征提取能力，該文算法總體準確率可達91.7%，而HSDH算法總體準確率只有47.2%。雖然HSDH算法被認為是一個好算法，但是僅僅局限于具有簡單循環基元的圖案，未考慮到織物具有豐富的紋理特征的影響。對比HSDH算法，該文算法具有較好的綜合性能，能夠對織物的循環圖案基元進行準確的分割。

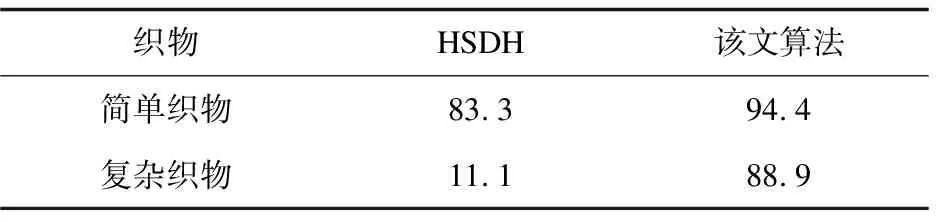
表1 算法準確率 %

3 結束語

針對印花織物循環圖案基元自動分割難度大的問題，該文提出了一種基于卷積神經網絡的織物循環圖案基元分割算法。實驗結果表明，對比HSDH算法，該文算法不僅可以分割出簡單織物的循環圖案基元，在復雜的織物上也有很好的分割效果。該算法具有很好的適應性和準確率。但是該算法在實際應用中還存在一定的局限性，因為需要對預訓練網絡所有的卷積層進行計算，使得計算時間相較于傳統方法更長。未來，會繼續考慮計算效率，對算法的結構進行優化以進一步提高計算速度，從而適用于更多的場景。