例析阿波羅尼斯圓的命題策略
廣東省佛山市羅定邦中學 龍 宇 528300
在近幾年的高考題、模擬題中,阿波羅尼斯圓(以下簡稱阿氏圓)越來越受到出題老師的青睞.筆者在梳理相關材料時,總結了該圓的幾種考察方式,現整理成文,以饗讀者.
1 阿氏圓的定義[1]
在平面上一點P到兩個定點的距離之比滿足=λ(λ>0 且λ≠1),則點P的軌跡是圓,這個圓便是經典的阿波羅尼斯圓.該圓的最直接考察則是利用定義求解,此類問題的特點在于給出確定的兩個定點及相關比例.此類問題的最經典形式便是2008年江蘇卷第13題,具體題目如下:
例1 滿足條件AB=2 ,AC=的△ABC的面積的最大值是_____.
解析:如圖1,以AB的中點O為原點進行建系,則點A,B的坐標為(-1,0),(1,0),設點C的坐標為(x,y)代入條件AC= 2BC,化簡可得點C的軌跡方程為:(x-3)2+y2=8,即圓心為E(3,0),r=2 2 的圓.

圖1
△ABC的面積的最大值問題轉化為點C到x軸距離的最大值問題.根據平面幾何的相關知識可知,點C到x軸距離≤CE=2 2 .對應的△ABC的面積的最大值為2 2 .
2 阿氏圓與其他圓錐曲線的結合
在阿氏圓的定義中,涉及到兩個定點與定比例.在常見的圓錐曲線中,也涉及到較多的定點與定值,這就為兩者的結合提供了理論基礎.
例2 (2019 年佛山二模第15 題)已知拋物線x2=2py(p>0)的焦點為F,準線為l,點P(4,y0)在拋物線上,K為l與y軸的交點,且|PK|=|PF|,求y0的值.
分析:本題的關鍵在于|PK|=|PF|,而拋物線的意義則是提供兩個定點K,F.結合阿氏圓的定義即可求解.解析:由題意可得K(0,-),F(0,),設點P的坐標為(x,y).由題意可得點P的軌跡為x2+(y-p)2=2p2.且點P的橫坐標為4,且點P在拋物線上,聯立方程即可得p=4,則有y0==2.
3 阿氏圓的逆向考察
在阿氏圓的定義中,涉及到兩個定點、定值以及最終的軌跡圓.能否根據圓以及定值來考察兩個定點之間的關系呢?或者考察定值的范圍問題呢?
例3 (2021 年佛山高二期末試題第16題改編)如圖2,已知點A(4 7,0) ,B(0,3) ,圓O:x2+y2=4,設點P為圓O上的動點,求3PA+2PB的最小值.分析:所求式為:3PA+2PB=3(PA+PB).若其中PB可轉化為點P到另一定點的距離,則可將原問題轉化為圓上一點到兩定點的距離之和的最小值問題.本題是阿氏圓的逆向應用題,即通過點B及圓O求出另一個定點.

在上述解答過程中出現了三個方程,而僅有兩個未知數,說明該題的構造過程有一定的確定性.比如將原問題轉化為3PA+2PB=2(PA+PB) ,能否找到一點D使得PD=PA,且保證點P的軌跡為圓O呢?通過計算可知這樣的點D并不存在.
例4 (自編)已知點A(1,0),B(2,0)以及圓O:x2+y2=1,設點P為圓O上的動點,若|PB|=λ|PA|,求λ的取值范圍.
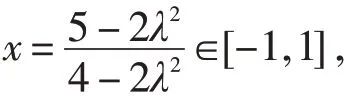
4 阿氏圓在立體圖形中的應用
例5 如圖3,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=2 ,BB1= 2 π ,∠ABC=90°,點M為AB的中點,點P在三棱柱內部或表面運動,且|PA|=|PM|,動點P形成的曲面將三棱柱分成兩個部分,體積分別為V1,V2(V1<V2),求的值.

圖3
分析:本題的關鍵條件是|PA|=|PM|,結合類比平面中阿氏圓的定義,猜想動點P的軌跡是一個球.本題可通過軌跡的思想來研究形成兩部分幾何體.
解析:為了便于研究點的軌跡,結合圖形特點,以點B為原點,BA為x軸,BC為y軸,BB1為z軸建立空間直角坐標系.即可得點A,M的坐標分別為(2,0,0),(1,0,0),設點P的 坐 標 為 (x,y,z). 代 入 條 件|PA|=|PM|可得點P的軌跡方程為x2+y2+z2=2 ,即以點B為球心,r=的球,本文稱其為阿波羅尼斯球.且平面ACC1A1與該球相離,故可知動點P 形成的曲面將三棱柱分出一部分體積為以B 為球心以ffffc3為半徑的球的ffffc2 ,對應的體積V1=ffffc1V球B=ffffc0π.整 個 三 棱 柱 的 體 積V=2 2 π ,則有V2=V-V1=ffffbfπ ,即可得

