高考、強基、競賽三個維度解高考解析幾何題

本文對2021 年高考解析幾何壓軸題分別從高考、強基、競賽三個維度進行解析，供普通考生、競賽生、教師參考.

題目：在平面直角坐標(biāo)系xoy中，已知點F1(-0),F2(,0)，點M滿足MF1-MF2=2.記M的軌跡 為C.（1）求C的方程；（2）設(shè)點T在直線x=上，過T的兩條直線分別交C于A,B兩點和P,Q兩點，且TA·TB=TP·TQ，求直線AB的斜率與直線PQ的斜率之和.

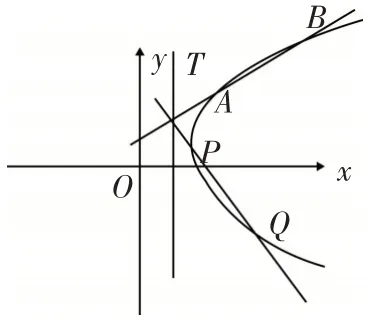
圖1

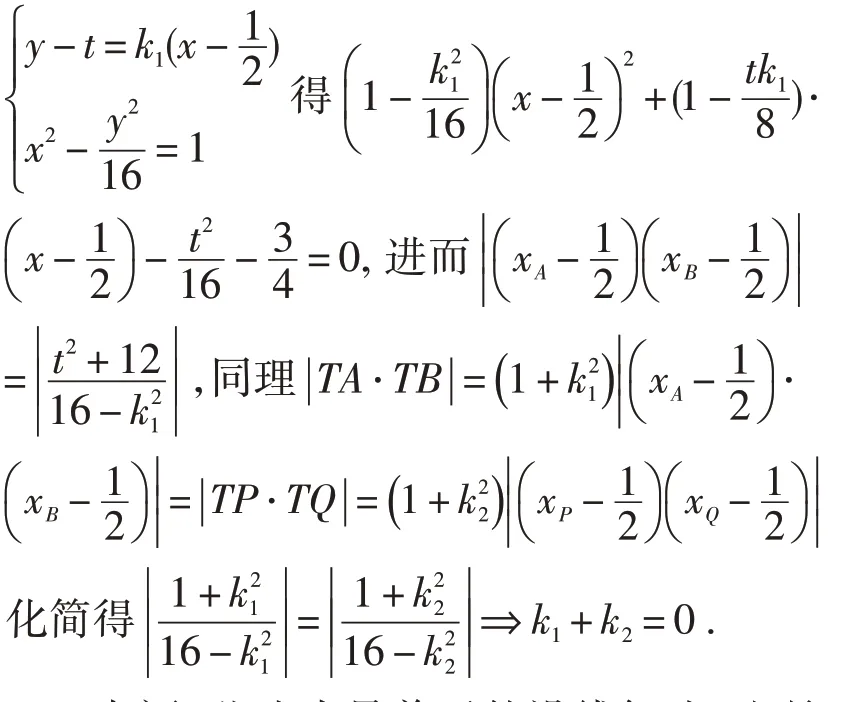
點評：此法為最普通的設(shè)線解法，也是學(xué)生必須熟練掌握的解法. 邏輯思維就是通過設(shè)線得到韋達(dá)定理，進而采用設(shè)而不求的思想解決問題.

點評：此法通過直接設(shè)點，通過點的坐標(biāo)解決問題，對直線參數(shù)方程的幾何意義要熟練.

點評：此法為競賽曲線系解法，通過曲線系可以大大減少運算量.

后記：對于一道題目，解題者所站的高度不同，那么解法的簡潔度會存在著巨大的差異.