從“高觀點”視角引發高階思維

周衛東

[摘 要]培養和發展學生的高階思維已經成為各國教育教學的目標之一，然而對高階思維培養方式并未達成統一認識。“高觀點”視角下的數學教學，可以從學科的本質屬性、思想內核及結構關聯等方面為高階思維的培養提供新的生長點。文章從理論層面對高階思維與“高觀點”的定義及兩者之間的關系進行了辨析，并立足教學實踐，建議從關注核心意義、關注上位知識、關注思想方法及關注結構關聯等方面來培養學生的高階思維。

[關鍵詞]高階思維;高觀點;核心意義;上位知識

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2022）14-0001-04

近年來，高階思維及其培養引起越來越多教育工作者的重視，然而從現狀觀之，關于高階思維，在理論界并未形成統一認識，且實踐層面也缺少科學且有力的指導，因此，學生高階思維的培養更是需要進一步研究。

一、理論辨識：高階思維與“高觀點”

1.關于高階思維

1987年，Resnick第一次提出高階思維的概念，明確了“非算法的、復雜的、有多重解，需要應用多種標準和學習者的自我調節，通常涉及不確定性”是高階思維的主要特征。也有一些學者從思維水平的角度來定義高階思維，比如將高階思維與布盧姆的認知目標分類建立對應關系，將思維過程具體化為六種水平，由低到高分別是記憶、理解、應用、分析、評價、創造，其中，記憶、理解、應用對應低階思維，分析、評價、創造對應高階思維。

那么，如何培養學生的高階思維呢？國內外已有的研究成果中，仁者見仁，智者見智，但也有一些共同之處：圍繞高階思維的三個方面“分析”“評價”“創造”，從教與學方式的改進層面進行了大量的實踐探索，體現了皮亞杰所倡導的“教與學對應”的思想;而對催生或提升高階思維的學科背景、學科內核和學科內在聯系，體現“教也要與學什么對應”“教與學科對應”的教學思想卻鮮有涉及。這，恰恰是高階思維培養中不可缺少的關鍵要素。

美國學者恩尼斯曾歸納了高階思維的三種教學實踐模式。一是“過程”模式。它強調思維技能的專門、直接教學，即將思維技能獨立于正規課程之外。二是“內容”模式。這種模式認為某些認知技能是特定于具體學科的，如數學和科學，應該在學科背景下進行教授。三是“注入”模式。它是將思維技能的教學與課堂的講授融合在一起。另一位學者科斯塔則歸結了“注入”模式所具有的優勢：第一，熟練的思維不可能在真空中進行;第二，學科性質會限制問題解決的過程。學習內容決定了思維技能的選擇和應用，思維技能的選擇和應用又形成了所學習的內容的視角和知識……總體上說，基于“注入”模式進行高階思維教學，在學校教學中更為常見。從教學實踐的具體情況來看，筆者非常認同“注入”模式，即將高階思維的培養融入鮮活的、有意義的具體內容之中，“使教學產生最大化的影響，使所有學生，即使不成為科學家，也能通過在自己的生活中使用高階思維，成為仔細、熟練的思維科學家”。

高階思維的培養，不像一般思維的培養那樣，有若干現成的經驗可以借鑒，有若干經典的課例可以參考。高階思維的培養，無論是在理念層面還是策略層面上，都需要跳出常規、躍升高度，需要“高觀點”的引領。

2.關于“高觀點”

論起“高觀點”的出處，當數德國數學家菲利克斯·克萊因的《高觀點下的初等數學》這本書。這是一本影響深遠的教育論著，書中指出：“有許多初等數學的現象只有在非初等的理論結構內才能深刻地理解，例如在實數域里不好理解的某些東西，從復數域的觀點看，就清楚了;在歐氏空間里某些不好解釋的現象，從射影空間的觀點看，就有滿意的說明”“教師應具備較高的數學觀點，觀點越高，事物就越顯得簡單”……這些都是“高觀點”最根本的內涵。教學研究是需要想象力的。綜合分析當下數學教學實踐中的成功經驗與存在弊端，完全可以建構屬于“我”的關于“高觀點”的理解與實踐。（本文提及的“高觀點”，帶有更多的自定義成分）

高階思維所帶來的風景一定在遠方，在深處，在高點。高階思維的培養，需要新的視角、新的理解和新的實踐來實現和詮釋。通過關注核心意義、關注上位知識、關注思想方法、關注結構關聯等途徑，促進高階思維的持續發生，能使小學數學教學呈現一派新的景象與新的生機，從而更好地為學生的數學學習服務。

二、實踐探問：從“高觀點”視角促進高階思維提升

高階思維不會自動生成，也不能一蹴而就，需要教師以真誠的態度與智慧的教學促其孕育、生成與發展。

1.高階思維在關注核心意義的過程中提“純”

高階思維應該著力在學科的最核心處。美國著名的數學教育家赫斯認為：“數學教學的問題并不在于尋找最好的教學方式，而在于明白數學是什么，如果不正視數學的本質問題，便永遠解決不了教學上的爭議。”一般認為，數學知識的本質，既表現為隱藏在客觀事物背后的數學原理、數學規律，又表現為隱藏在數學知識內部的本質屬性。數學知識的本質，也就是數學知識的核心意義。“高觀點”視域下的數學教學，追求的不僅僅是本質屬性的一般理解，更是對核心意義的深耕。

比如“三角形的穩定性”的教學，教師通常是讓學生用木條做一個三角形的框架，再做一個四邊形的框架，然后讓學生用手去拉這兩個框架。學生發現，怎么拉三角形的框架都不變，而輕輕一拉四邊形的框架，就變形了。這時，教師小結：“這個實驗告訴我們，三角形具有穩定性，四邊形具有易變性。”這樣的教學，著力在知識的淺表理解，學生經歷的是低階思維的過程。對此，曾有一學生提出這樣的問題：“我爸爸是個焊工，一次他用鋼筋焊接了一個四邊形的框架，我怎么拉都拉不動，是不是也可以說明四邊形具有穩定性呢？”教師無言以對。是啊！所有的解釋在此時此景中都顯得蒼白無力。這告訴我們：促成學生對三角形的穩定性的理解，不能只依靠“用手拉”這樣淺表的實驗，而是要激活學生的高階思維，讓學生理解知識背后更為核心的原理。

慶幸的是，現行的人教版教材已經改變，通過五個層次讓學生對三角形的穩定性有了感知和體驗。（1）放手實踐：學生準備若干根一樣的小棒，先用小棒擺一個三角形，再用小棒擺一個四邊形，然后進行展示。（2）引導分析：通過思考問題“你發現了什么？”，學生發現，不同的人擺出的三角形的形狀、大小都是一樣的，而不同的人擺出的四邊形的大小、形狀卻少有一樣的。（3）明確原理：在學生充分感知后揭示“擺出的三角形的大小、形狀一樣，說明三角形具有穩定性，而擺出的四邊形的大小、形狀不一樣，說明四邊形具有易變性”。（4）及時評價：出示一些生活場景，讓學生辨析哪些地方用到了三角形的穩定性。（5）引發創造：提供一把搖晃的椅子，讓學生思考“怎樣才能讓它穩固不搖”。這樣的教學，著力在知識最核心的部位，引導學生經歷概念形成的全過程，實現了知識本質精準把握與思維能力有效提升的雙向建構。

2.高階思維在關注上位知識的過程中蓄“力”

高階思維的培養需要一定的“勢能”來助力，美國教育心理學家奧蘇伯爾所做的有關上位知識的研究完全可以實現這一愿景。上位知識，位于學科知識金字塔的頂端，其抽象性、概括性、包容性最高，解釋力最強。用生物學術語來說，上位知識就是學科知識體系的DNA，它內含遺傳密碼，最具再生力、生發力和預示力，是最具活性和繁殖性最強的一種知識類型，是其他知識得以生發與依附的主根。從學生學習的角度來看，上位知識是一個綱，綱舉目張;是一個組織者，整合所學的知識;是一根紅線，把知識串聯起來。如果說學科知識體系具有“鷹架”式結構，那么，上位知識就是撐起這一“鷹架”的支點。抓住了上位知識，其他知識和相應的學習活動就可以被提起來。可以說，上位知識是整個學習活動的連心鎖，是賦予學習活動整體性的關鍵。

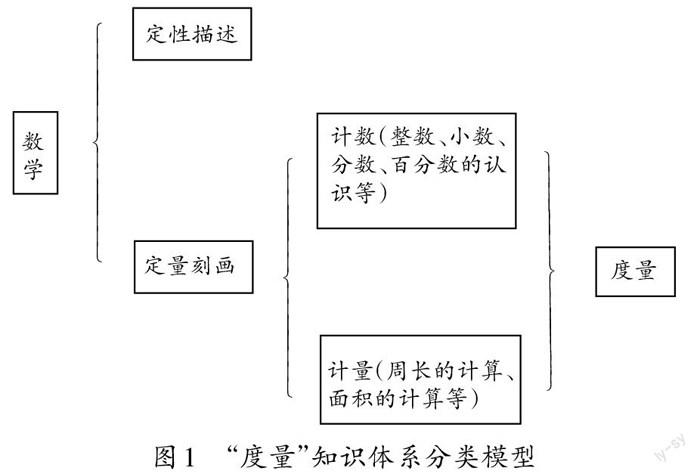
比如，放眼整個數學知識體系，數學可分為定性描述與定量刻畫兩部分，而定量刻畫又可分成計數與計量兩類，納入 “度量”這一大概念之中（如圖1）。無疑，“度量”是所有定量刻畫知識的上位知識。“度量”的教學過程不能是簡單授予，而要把學生置于一個強大的思維場中，引發學生高階思維的產生。（1）引發沖突：確定標準、研制單位（確定統一的標準）;（2）想象創造：制造工具、計量個數（對標準逐一計數）;（3）高階思維：簡便計數、構造模型（依特征簡便計數）。因此，包括整數、分數、小數、百分數等在內所有的計數教學，與包括周長的計算、各種幾何圖形面積的計算等在內的計量教學，都可以用“度量”這一大概念體系方法進行統整，且統整后的教學內容更能為學生高階思維的形成創造條件。

3.高階思維在關注思想方法的過程中賦“魂”

學科思想和方法是學科知識中的“隱性內容”，是學科專家提出的對今后學科發展和學科學習最具影響力的那些觀念和見解，是知識“背后”的知識，也是高階思維的精髓與靈魂，是學科思維的“軟件”，其基于學科知識，又高于學科知識，與學科知識具有不可分割的辯證關系。因此，如何引導學生一起去找尋和發現數學中包含的思想、方法及解決問題的策略是數學教師面臨的最大挑戰，因為如果內容選不準，不僅會浪費師生寶貴的時間，還會錯失學生智慧生長的“黃金期”。數學教學就是要幫助學生逐步建構起自己的思想體系、方法體系和策略體系，進而從不同的角度理解和認識問題，創造性地解決問題，進而發展高階思維。

首先，從整體上構建教材中所蘊含的數學思想的立體框架。比如教學蘇教版教材的“三位數乘兩位數”時，如果“就事論事”進行淺表性分析，其實很難看到其中的思想內核。教師可在復習兩位數乘兩位數的計算后，讓學生直接嘗試三位數乘兩位數的計算并說明道理，之后通過追問引發學生的高階思維：“老師翻看了后面的教材，在四年級學完了三位數乘兩位數之后，不編排四位數乘兩位數或三位數乘三位數了，這是為什么呢？”這樣的追問意在讓學生通過思考明白，所有多位數的乘法都蘊含著一種運算思想，那就是“先分后合”，無論運算步數如何變化，隱含其中的思想原理是不變的。

其次，讓數學思想有機融合在數學知識的形成過程。比如，一年級上冊有這樣的習題：

6-□>4 ? ? ? ? ? 12>4+□ ? ? ? ?6+□<10

7<15-□ ? ? ? ? □+8<13 ? ? ? ?10>5+□

雖然這些題目只是要求學生在空格中填進一個合適的數，但教師應該明白，若把□換成x，則上面的題目就變成了不等式，這時x就是一個變元符號，也就會有一定的取值范圍，這一個“位置占有者”的作用就會凸顯出來。因此，教學時，教師可以引導學生思考、討論“□內最大能填幾？最小呢？最多能填幾個數？”等問題，以引發學生的高階思維。同樣，在此基礎上還可進一步深化：“□+○<7，可以填些什么數？”這樣能更好地滲透“符號變元”這一數學思想。

4.高階思維在關注結構關聯的過程中構“體”

美國學者恩尼斯認為：“能力強的學生把學習材料看成是系統的、有聯系的、能進行歸類和類比的，換言之，他們的精神世界是有組織的，能借助高階思維把瑣碎的信息組合成有體系的整體。”學科之所以為學科，而不是概念與知識的堆砌，其中非常重要的原因是學科知識之間存在著不可割裂的內在聯系。所謂結構，簡單地說，就是事物之間的聯系，它表現為組織形式和構成秩序。從靜態來看，學科知識應該形成經緯交織、融會貫通的立體網絡;從動態來看，學科知識應該形成一個自我再生力非常強大的開放系統。為此，教師必須合理地設計教學，編織一個具有生命力的、處于運動中的思維網絡，引導學生深刻領會各個概念的實質，掌握蘊含在各個概念相互關系中的思維模式。

比如，乘法的三個運算律（乘法交換律、乘法結合律、乘法分配律）之間是有內在關聯的，其本質是一致的，都是乘法意義的外在呈現。因此，教學“乘法分配律”時，有教師通過一張點子圖巧妙地將這三個運算律進行了統整：讓學生在點子圖上把“4×6=6×4”“4×3×2=4×（3×2）”“（5+1）×4=5×4+1×4”三道算式的運算過程表示出來。學生在問題的驅動下，經歷了數理表征、對比歸納等高質量的思維活動之后頓悟：無論是乘法交換律、乘法結合律還是乘法分配律，求的都是“幾個幾是多少”，都是根據乘法的意義衍生出來的。

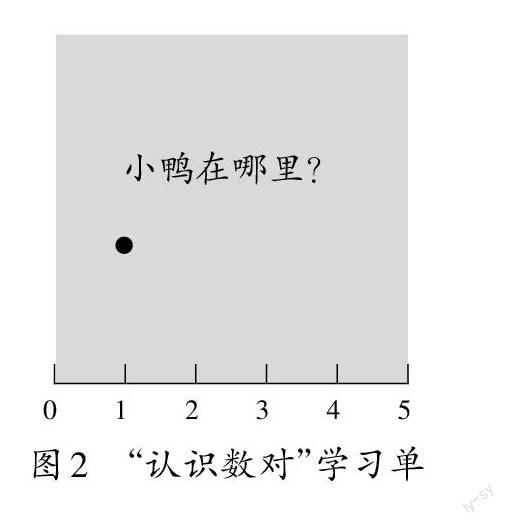
又如，“圖形與幾何”領域中“圖形與位置”的相關內容主要包括：（1）二年級用“第幾排第幾個”等方式描述物體的位置;（2）五年級用“數對”表示方格圖上點的位置;（3）六年級用“方向和距離”表示平面圖上點的位置。這三個內容雖然呈現不同的教學層次，但內在的數學本質是一致的，即都與“方向”“距離”這兩個要素密切相關。因而，教師教學“用數對確定位置”這一內容時，不僅要看到它的“今生”，還要看到它的“前世”與“后世”，即“它從哪里來”與“將往哪里去”。為此，在這節課的教學中，筆者創設了“小鴨在哪里”的情境（如圖2），首先通過回憶一維的“小鴨是怎么走的”，勾勒出全課的輪廓：一個點的位置，既與“起點”“方向”有關，又跟“數”有關。然后創設大情境，催生學生的高階思維：“小鴨來到了一個面上，這時小鴨在哪里呢？該如何表示呢？”讓學生自由想象、大膽創造。在學生的作品中，可以看到，無論是何種畫法，都有一個共性，那就是“創造”出了一根縱軸。最后，引導學生思考“為什么要有這根縱軸呢？”。教學至此，不但坐標雛形已應運而生，還有效而巧妙地滲透了坐標思想。

在學生理解了數對的原理及簡單的運用后，筆者再引導學生對知識的形成過程進行回溯。此時學生已深刻地感受到，數對也跟起點、方向與距離有關，只不過在起點的前提下，方向和數量均由一個變成了兩個。于是，在結課時，筆者拋出畫龍點睛式的問題“要是小鴨潛到了水底，該怎么確定它的位置呢？”，以此聯系到三維空間里點的位置的確定，引發學生大膽想象。就在學生有了朦朦朧朧的感覺之時，教學戛然而止……此時，在學生的認知結構中“若隱若現”留下的，是知識的全貌，是結構的雛形，更是高階思維所帶來的對學習的高峰體驗。

其實，學生高階思維的培養，需要一個長期、動態的思辨和探索過程。而教師需要做的，正如克萊因先生所言，“保持一流大師的遺風：回到固有的生動活潑的思考，回到自然”！這便是高階思維研究的美好目標和應然追求。

（責編 金 鈴）