三角形三邊關系之“三探”

張小麗

[摘 要]三角形的三邊關系雖然只是一個基礎性結論，但通過操作探究得出才能令學生信服。在學生操作的過程中，教師不應過多地干涉或操控，否則學生得出的結論就是盲從的，學生只有經過獨立思考和自我覺醒，才能對知識的運用做到心領神會，融會貫通。

[關鍵詞]三角形;三邊關系;探究

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2022）14-0061-03

【教學案例】

師（課件出示形形色色、形狀各異的圖形）：你能識別出三角形嗎？

（學生很快找到了三角形，而且找得很齊全）

師：你們尋找的依據是什么？又憑借什么斷言它們是三角形？

生1：只要含有三條邊、三個角的幾何圖形就可以認定為三角形。

生2：不對，應該說由三條線段首尾順次相接組成的圖形叫作三角形，而三角形含有三條邊、三個角和三個頂點。

師（圖片演示）：由三條線段首尾順次相接圍成的圖形是三角形。

師：假若提供三條線段，你有把握能圍成一個三角形嗎？

生3（胸有成竹）：能。

（教師發給學生8厘米、10厘米、15厘米的竹簽各一根，學生上臺演示，順利完成任務）

師（教師再發給學生3厘米、10厘米、15厘米的竹簽各一根，學生搗鼓半天，始終無法如愿）：通過剛才的兩次嘗試，你們有沒有發現什么蹊蹺？

生4：三根竹簽圍三角形，有時成功，有時失敗。

師：一語中的！那么什么時候會成功，什么時候會失敗？這其中到底有什么奧秘？三角形的三邊之間是否存在某種不為人知的微妙聯系呢？這就是我們本次課的學習重點。

評析：教師利用學生思維中的“漏洞”和思想上的“麻痹”，讓學生自行拼接三角形，并且故意配給兩組拼接結果截然不同的竹簽，制造了認知沖突。在成敗得失之間，學生對三角形的三邊關系產生了強烈的好奇心。從三角形的表面看，學生最初誤認為任意三條線段就能組成三角形，但通過動手拼接，認知結構發生改變，開始意識到三角形的三邊之間定然存在某種微妙關系，而這種關系直接決定能不能圍成三角形。該教學是較為常見的模式，大部分教師都用這種方法。下面利用“三探”對該教學進行創新性的改進。

一、獨立自主探究

【教學片段1】

師：老師給每個小組發一個匣子，匣子里有五根竹簽，要求大家通過這五根竹簽的拼接，探索出三角形三邊的關系。

課件呈現合作須知：

（1）從匣子中存放的五根竹簽（長度分別為4厘米、6厘米、8厘米、10厘米、15厘米）中隨機抽取三根，試著拼接三角形。

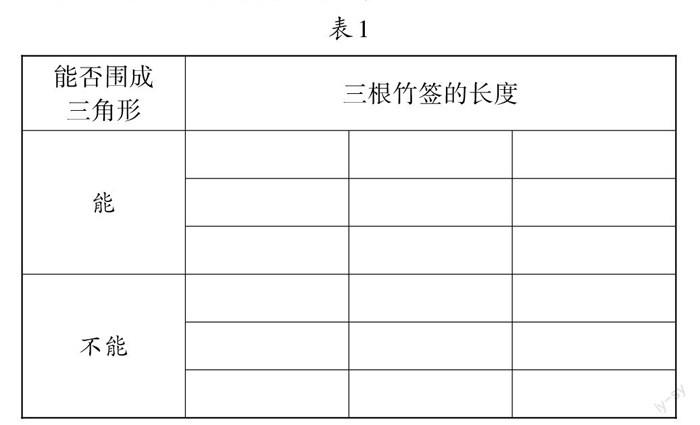
（2）小組共同探究，小組長負責記錄數據，包括竹簽長度和拼接成敗。（見表1）

（3）綜合分析本組多次實驗的結果，并回答以下問題：如果能夠圍成三角形，三根竹簽需要滿足什么條件？什么情況下會拼接失敗？

評析：課本的原意是準備四組竹簽先讓學生操作，然后通過列式比較大小來推導三角形的三邊關系，如此設計固然直截了當，但是在操作之后就迫不及待地要求學生列式，從定性分析直接上升到定量分析，未免有些突兀和操之過急。學生被教師牽著鼻子走，被迫去操作、計算，得出的結論自然也不是學生自己發現的。為什么一定要拿兩邊之和與第三邊做比較，比較其他的關系就不行嗎？顯然，如此探究不過是學生在教師的授意下做出的妥協與順從。鑒于此，筆者對該部分做了加工和改進，改為“發給學生五根不同長度的竹簽，讓學生隨機抽選三根進行拼接實驗，并從中歸納出定律”。這樣，學生就能通過操作活動體驗到三邊之間的長度關系能夠左右拼接的成敗，然后通過對大量實驗數據的對比，從中歸納出三角形的三邊關系。

三角形的三邊關系是一個抽象的幾何關系，是定性分析的結果，那么就意味著無法采用一般的邏輯推理法去推導，因為沒有特殊和一般之分，所以無法進行演繹推理，也無法進行合情推理，只能用直觀演示法來揭示，即讓學生在大量的隨機實驗中發現不尋常的地方，產生認知沖突：為什么有的竹簽可以拼接成三角形，有的卻不行。在好奇心的驅使下，學生就會積極主動探究，通過對比觀察，理性歸納出三根竹簽能圍成三角形的必要條件。

二、小組合作探究

【教學片段2】

活動環節：學生4人一組開展探究活動，一人拼接竹簽，小組長記錄竹簽長度和實驗成敗，其他組員觀察數據并綜合分析。教師巡檢督導，傾聽學生意見。

匯報環節：各組派代表上臺匯報本組的實驗情況，教師綜合各組的數據，整理出一份規范的記錄單（見表2）。

生1：我覺得長度分別為4厘米、6厘米、10厘米的三根竹簽也能拼接成一個三角形。

師：真的嗎？可否讓大家開開眼界。

（由于學具可彎曲，生1拼成了“三角形”。）

生2：生1的竹簽有些畸形，湊巧而已。

生3：從理論上講根本無法拼成三角形，因為兩根短竹簽的長度加起來等于第三根竹簽的長度，兩根短竹簽連起來會與第三根竹簽重合成一條線，無法拱起形成犄角。

師：言之有理，我們來看看動態演示。（動態演示的結果顯示：長度分別為4厘米、6厘米、10厘米的三根竹簽無法拱起形成犄角）

師：什么情況下三根竹簽無法圍成三角形呢？

生4：當其中兩根短竹簽的長度和小于或者等于長竹簽時無法圍成三角形。

師：那么若要圍成三角形，對三根竹簽的長度有什么要求呢？

生5：當兩根較短竹簽長度之和超過第三根較長竹簽時，就能拼成三角形。

師：分析得很到位，由此可以推斷，三角形的三邊必然存在某種關系。

生6：兩短邊長度之和必然超過最長邊。

生7：任意兩邊之和必然大于第三邊，不然就無法構成三角形了。

師：“任意”二字切中了要害，還道明了其中原委。誰能再精簡一下？

生8：在三角形中任意兩邊的和大于第三邊。

評析：“紙上得來終覺淺，絕知此事要躬行。”教師直接告知結論，學生未必記得住，就算記得住也未必信服，而學生在動手操作中發現并通過檢驗證實有效的結論，則會給學生留下深刻的印象。學生通過對操作中遇到的兩種截然不同的現象進行對比辨析，發現其中的規律，從而歸納出三角形的三邊關系。從發現問題、產生疑問，到收集、整理、分析數據，初步發現操作性的實驗規律，然后轉化成理論成果，學生在教師的操作指導下，獨立完成了一次數學理論研究，不僅掌握了相關知識，而且學到了科學的研究方法。

很多課堂上隨機抽取木棒嘗試圍成三角形的實驗，還只是停留在感性認知的層面，在這樣的實驗中，學生隱隱約約感到三邊的差距不能太大，但是又說不清楚到底是多少才合理，無法定量分析出個所以然來。可見完全靠直觀法終究無法得出確切的結論，因此數字化的定量探究過程是必要的，只有用數據說話才能令人信服，也最能讓規律外顯。于是，學生將所選的組合長度記錄下來并制成表格后，在大量數據中，學生發現，三邊之間的差距其實可以通過算式來具體表達，即最短的兩邊長度之和不能小于最長的邊。當教師指引學生弄清兩邊之和等于第三邊也無法圍成三角形的原委之后，學生最終才能下定結論：三角形任意兩邊之和大于第三邊。

三、拓展探究

【教學片段3】

出示（教材第31頁第1題，題略）：勾選能擺成三角形的竹簽。

生1：第一組和第三組可擺成三角形，因為任意兩根竹簽的長度之和大于第三根竹簽。第二組不能，因為本組有兩根竹簽長度之和等于第三根竹簽。

生2：不用成對逐項篩查，只需直接判斷最短兩邊之和與最長邊的大小關系即可一錘定音。

出示（教材第31頁第2題，題略）：從下面五根竹簽中隨機抽選三根，嘗試擺出兩個不同形狀的三角形。

師：拼接前先設想“擺出的三角形會是什么樣子”，然后再動手操作，對比一下是否與設想的相符。

生3：我擺出了兩個三角形，一個是等邊三角形，另一個是等腰三角形。

生4：我擺出了兩個三角形，一個是鈍角三角形，另一個是銳角三角形。

……

出示題目：如果已知三角形的兩條邊的長分別是5厘米和8厘米，那么第三邊的長度范圍是多少？

生1：第三邊長度應該介于3厘米和13厘米之間。

師：愿聞其詳。

生1：因為三角形任意兩邊之和要大于第三邊，若將8厘米的邊作為最長邊，第三邊加上5就應該大于8，所以第三邊就應該大于3;若將第三邊作為最長邊，那么第三邊要小于5+8=13，而5厘米的邊不可能設為最長邊，因此只需考慮以上兩種情況。

生2（若有所思）： 8-5=3，8+5=13，第三邊就處于這兩個結果之間。

師：是不是三角形中任意兩邊的差都小于第三邊呢？大家不妨證實一下。

師：可以借用前面可以圍成三角形的三邊數據。

出示數據：

生3（再次回顧前面的實驗數據，對照觀察發現新結論）：6-4<8，8-4<6，8-6<4，沒有一個例外，所以三角形任意兩邊的差都小于第三邊的結論成立。

評析：在研究出三角形任意兩邊之和大于第三邊的定理后，筆者設置開放性問題，給定兩邊長度，讓學生確定第三邊長度的取值范圍。這次不再是判別能不能構成三角形，而是要通過運算確定邊長，引發學生深度思考。這個思考是多向的、全面的，之前只需要直接兩兩求和進行對比，現在出現一個不確定元素，這個元素既可以作為最長邊，又可以作為非最長邊，所以會出現一個取值范圍，而且需要換位運算，從而引出作差的需要。

應用三角形的三邊關系推算第三邊的長度取值范圍，必須將三角形的三邊關系結論進一步拓展，才能得出另一個對稱結論——三角形兩邊之差小于第三邊。要想得出第一個基本結論的“姊妹篇”，還得轉向定量分析：給定三角形的兩邊長度，然后根據第一個基本結論推算出第三邊的長度取值范圍。這個過程對學生來說非常復雜，邏輯性非常強，因為推算出第三邊的長度取值范圍后，還要再根據三邊相對精確的長度關系反推出結論。至此，三角形的三邊關系才算徹底明朗，而這個最終結論是在定性分析與定量分析交替進行中得出的。

（責編 羅 艷）