摩擦阻尼器-拉索系統振動特性試驗研究

周海俊 何紀元 楊夏 向寧

摘 要：為研究拉索摩擦阻尼器的減振效果，開展了附加摩擦阻尼器拉索的自由振動和強 迫振動特性試驗.首先進行銅-鋼金屬摩擦阻尼器模型的力學性能試驗，得到螺栓扭矩與摩擦力之間的關系.然后進行摩擦阻尼器-拉索系統模型自由振動特性試驗研究，由試驗測得的自由振動位移衰減曲線得到對數衰減率，分析得到對數衰減率隨振幅的變化規律，并與現有理論進行對比.通過快速傅里葉變換和小波變換對自由振動加速度時程進行頻譜分析和時頻分析得到模態頻率變化情況.最后進行拉索-摩擦阻尼器系統的不同激振力-控制強迫振動試 驗，通過掃頻方式得到拉索振幅與激振頻率的關系，研究摩擦阻尼器對拉索共振幅值的影響.試驗結果表明摩擦阻尼器可以有效地減小小幅與大幅激振力時強迫振動的共振幅值;兩者相比，摩擦阻尼器在大幅激振力作用下減振效果更顯著.

關鍵詞：摩擦阻尼器;拉索;模態阻尼比;強迫振動;頻譜

中圖分類號：U448.27，TB123 文獻標志碼：A

Experimental Study on Vibration Characteristics of Friction-damper-cable System

ZHOU Haijun1，2，HE Jiyuan1，2，YANG Xia1，2?，XIANG Ning1，2

（1.Institute of Urban Smart Transportation & Safety Maintenance，Shenzhen University，Shenzhen 518060，China;

2.Guangdong Provincial Key Laboratory of Durability for Marine Civil Engineering（Shenzhen University），Shenzhen 518060，China）

Abstract：Vibration characteristics of cable models with friction damper are studied experimentally.Firstly，the mechanical properties of the friction damper model made of copper and steel were tested.The relationship between torque and friction force of the damper bolt was obtained.Secondly，the experimental study on the free vibration char-acteristics of the friction damp-cable model was carried out.The logarithmic decay rate was obtained from the free vi-bration decay of displacement.The relationship between the logarithmic decay rate and vibration amplitude was ana-lyzed and compared with theoretical results.The free vibration acceleration time history was analyzed by the Fast Fourier Transform and Wavelet transform to derive the change of frequency spectrum with time.Finally，forced vibra-tion tests of the friction damper-cable system were carried out.The relationship between cable amplitude and excita-tion frequency was obtained by sweep-frequency technique.The mitigation effects of friction damper on cable reso-nance amplitude were investigated.The test results show that the friction damper can effectively reduce the reso-nance amplitude of forced vibration under small or large amplitude excitation.Friction damper was more efficient for the mitigation of amplitude excitation.

Key words：friction damper;cable;modal damping ratio;forced vibration;frequency spectrum

斜拉索是斜拉橋的主要受力構件，由于其質量輕、阻尼低、柔度大，故極易在外界激勵下產生各種類型的振動[1-5].持續大幅振動會引起諸多次生問 題，如拉索錨固端疲勞破壞、保護套開裂等，從而縮 短斜拉索的使用壽命，帶來不可估量的經濟損失.目 前拉索減振已成為大跨徑斜拉橋建設和維護中亟須 解決的關鍵問題之一.工程中常采用的斜拉索減振 措施包括機械措施（增加阻尼器）、結構措施（安裝輔 助索）和氣動措施等[6-7].阻尼器具有減振性能穩定等突出優點，在工程應用中被普遍采用[8-9].常見的線 性黏滯阻尼器往往針對某一階特定模態進行優化，但 拉索的振動往往存在多階模態耦合，線性黏滯阻尼器并不能很好地抑制拉索多模態振動.已有研究表明摩擦阻尼器對于各階模態均可達到最大模態阻尼比，故可更有效地抑制阻尼器-拉索系統多模態振動[10].

已有較多學者采用不同的方法（如有限元建模分析、諧波平衡法等）對摩擦阻尼器-拉索系統進行研究，初步揭示了摩擦阻尼器的非線性作用機制并 確認其可以有效地抑制拉索振動[10-12]，但由于摩擦阻尼器的強非線性，影響摩擦阻尼器減振效果的因 素較多，非常有必要進行摩擦阻尼器-拉索系統模型 振動試驗并分析其減振性能，以便進一步優化摩擦阻尼器，使之達到更好的減振效果.本文設計制作了銅-鋼金屬摩擦阻尼器，并進行了摩擦阻尼器-拉索系統模型的自由振動和強迫振動試驗，研究分析摩擦阻尼器的減振效果及相關參數的影響.

1拉索模型

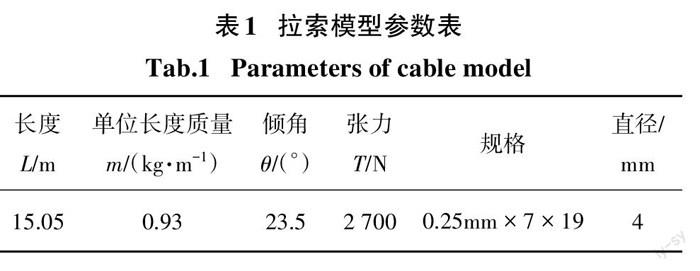
本文取蘇通大橋 Z16 號拉索為原型，拉索弦長303.95m，索力4178.7kN，單位長度質量68.6 kg/m，傾角36.34°，基頻0.406Hz.拉索模型縮尺比為1∶20，原型索與拉索模型的索重之比約為兩者的索力之比，原型索與拉索模型具有較高的相似性.拉索模型的參數詳見表1.為使模型拉索的基頻和原型拉索滿 足相似律，拉索模型每隔10cm安裝一個配重銅塊，質量為86.7 g.該拉索模型較細長，因此本文不考慮抗彎剛度的影響.

2 摩擦阻尼器構造及標定試驗

2.1摩擦阻尼器模型

圖1所示摩擦阻尼器模型主要由摩擦片、擰緊 螺栓、索夾、固定支架以及環形支架組成.摩擦片采用黃銅片，索夾、擰緊螺栓、墊板、支架材料均采用Q235 鋼材.摩擦片嵌固在索夾上，擰緊螺栓固定在支架上，旋緊螺栓使得螺栓與摩擦片之間產生擠壓力，當拉索振動時，索夾隨之振動，摩擦片與擰緊螺 栓產生相對運動，從而產生摩擦力.通過調節擰緊螺 栓與摩擦片之間的擠壓力可調節摩擦力的大小.

摩擦阻尼器模型設計時首先需確定摩擦力大小.摩擦阻尼器的臨界工作振幅Acrit與摩擦力F0的關系見式（1）.[11]

式中：i為模態階數;l1為摩擦阻尼器距離拉索下錨固端的距離;T為拉索張力;L為拉索長度.臨界工作振 幅是指摩擦阻尼器剛開始工作時對應的拉索振幅.可見臨界工作振幅與模態階數成反比關系.

本文中l1=0.752 5m（l1/L=0.05），為安全起見，一階臨界工作振幅不宜過大，由式（1）可以確定 摩擦力F0與一階臨界工作振幅 Acrit的對應關系如表2所示.

2.2? 摩擦力標定試驗

采用微機控制電子萬能試驗機進行標定試驗，量程0～10kN，精度為±0.5%，力傳感器量程0～ 50kg.扭力起子型號 LTDK-1.5，量程0.01～0.15 N·m，精度為±5%.先將索夾與連接件通過螺栓固定，再通過插銷將連接件與電子萬能試驗機拉伸輔具連接固定，通過扭力起子對擰緊螺栓施加扭矩.單向拉伸加載控制方式為位移控制，加載速率為1mm/min，當拉力載荷克服摩擦阻尼器模型的靜摩擦力后，摩擦片 開始勻速滑動，此時拉力與滑動摩擦力的大小相等.

設定擰緊螺栓扭矩 T0的5個工況分別為0.05 N· m、0.10N·m、0.15 N·m、0.20N·m、0.25 N·m，圖2所示為其中3個工況的摩擦力時程曲線.可見，摩擦力時程曲線的變化規律基本相似，從t=0時刻開始，摩擦力先快速增長后趨于穩定.取摩擦力時程曲線水平段的平均值為該扭矩對應的摩擦力大小.

摩擦力F0隨扭矩 T0的變化如圖3所示，線性回歸得：

3 摩擦阻尼器-拉索模型

3.1 試驗設備及測點布置

圖4（a）所示為摩擦阻尼器-拉索系統模型試驗 示意圖.力傳感器安裝在上錨固端，4個激光位移傳 感器測量拉索模型面內振動位移，分別安裝在拉索模型摩擦阻尼器位置處、距下錨固端L/6處、L/4處、L/2處，加速度傳 感器安裝在距下錨固端L/3處.圖4（b）為摩擦阻尼器-拉索系統模型實物圖.試驗設備規格詳見表3.

3.2? 試驗過程及數據處理方法

激振器安裝在距離拉索模型下錨固端0.1L處，拉索上固定有法蘭克夾，采用尼龍線連接法蘭克夾和激振器激振桿.首先對摩擦阻尼器-拉索系統模型 進行正弦掃頻測得含有系統各階模態響應的位移時程曲線，通過快速傅里葉分析得到各階頻率.將測得的系統各階頻率輸入為激振器激振頻率進行激振，待拉索模型振動穩定后剪斷尼龍線，采集系統自由振動衰減運動時程數據.最后，通過激振器進行正弦掃 頻對摩擦阻尼器-拉索模型進行強迫振動激勵并記錄得到響應振幅.本實驗中數據采樣頻率為500Hz.

采用快速傅里葉分析對拉索自由振動的加速度數據進行分析得到拉索的振動頻率;根據濾波后的自由振動位移衰減時程數據計算對數衰減率δ，其計算公式見式（3）[13].

式中：Aj、Aj + k分別為相隔 k個振動周期的j時刻與j+k時刻的振幅.

4? 試驗結果

4.1 拉索模型自由振動

本文相隔 50個振動周期計算得到拉索模型面 內一階自由振動的對數衰減率，其平均值為0.39%.考慮拉索垂度的自振頻率fi 計算公式見式（4）[14].

表4所示為拉索模型面內前五階自振頻率試驗 值與理論值的比較.可以看出，面內自振頻率試驗值與理論值的誤差較小，理論值略大于試驗值的原因在于力傳感器安裝于拉索模型上端，其張力值相較于張緊弦理論的張力值偏大.

4.2? 摩擦阻尼器-拉索模型自由振動

摩擦阻尼器-拉索系統模型自由振動試驗設置 摩擦力F0工況為2 N、3N、4 N、5 N.圖5所示為摩擦阻尼器-拉索模型 L/2處面內一階自由振動衰減曲線（阻尼器安裝位置 l1/L=0.05，摩擦力F0= 5 N）.拉索L/2處面內一階自由振動衰減曲線在摩擦阻尼器將拉索鎖住之前近似呈線性衰減.自由振動衰減到臨 界工作振幅（約為8 mm）時，拉索在摩擦阻尼器位置處振動的恢復力小于摩擦力，此時摩擦阻尼器將拉索“鎖住”并停止工作，拉索通過內阻尼耗散振動能量，由于拉索內阻尼極小，拉索振動幅值衰減極慢.

其他摩擦力工況在L/2處面內一階自由振動衰 減曲線變化趨勢與圖5相似，故不再贅述.圖6（a）所示為在不同摩擦力工況下一階對數衰減率-振幅關系曲線的比較，對數衰減率為相隔 2個振動周期計算得到.可見隨著振幅的逐漸減小，一階對數衰減先 逐漸增大至最大值，然后急劇下降至接近于0.隨著 摩擦力的增大，一階對數衰減率-振幅關系曲線向右 平移，對數衰減率最大值無明顯變化，臨界工作振幅 逐漸增大.

在給定振幅和頻率下，令摩擦阻尼器在一個周 期內所做的功與等效線性黏滯阻尼器所做的功相等[15]，可得到對數衰 減率δ與振 幅 A的關系式，見式（5）.

將本試驗中的參數L、T、l1/L 代入式（5），得到對數衰減率δ隨振幅 A變化的曲線如圖6（b）所示.對比圖6（a）、圖6（b），可見對數衰減率試驗值和理論值隨拉索振幅變化的趨勢一致.

公式（5）中，對振幅 A 求導并令導數為0，可得到對數衰減率的最大值δmax，發現 δmax與F0無關，這與圖6（a）試驗結果相符.試驗結果相較于理論值，各工況下最大對數衰減率偏大，臨界工作振幅偏小.其原因是摩擦阻尼器具有強非線性，而模態阻尼比是基于線性黏滯阻尼假設，用模態阻尼比來評價非線性的拉索-摩擦阻尼器系統的阻尼會導致一定的誤差.

圖7所示為面內一階加速度時程曲線與頻譜圖（l1/L=0.05，F0= 5 N）.可見摩擦阻尼器-拉索系統面內一階振動含有多階模態頻率成分，圖中標出了一、二、三階振動頻率.對摩擦阻尼器-拉索系統自由 振動的一階加速度數據做連續小波變換分析表明，一階頻率在12 s時發生了小幅度增大的“偏折”，這與阻尼器將拉索鎖住導致頻率增大的現象吻合;進一步分析表明，一階振動頻率在拉索鎖住之前就有隨時間而增大的趨勢.摩擦力F0= 2 N、3N、4 N 工況下的面內一階加速度時程與頻譜圖和F0= 5 N 工況相似，此處不再贅述.

4.3 摩擦阻尼器-拉索系統模型強迫振動

本節參考 Xu等[16]研究方法，分析摩擦阻尼器對小幅激振力與大幅激振力時拉索強迫振動共振幅值的減振效果.設置掃頻范圍1～12hz，一階共振區域 掃頻速率為0.02hz/s，二至五階共振區域掃頻速率為0.04Hz/s，摩擦阻尼器摩擦力設為2 N.一、三、五階面內位移由 L/2處的激光位移傳感器測得，二階面 內位移由 L/4處的激光位移傳感器測得，四階面內位移由 L/6處的激光位移傳感器測得.

激振器產生的激振力設為5 N，得到小幅激振力時，無阻尼器及有阻尼器拉索模型強迫振動面內一階及五階振幅-激振頻率關系的比較如圖8所示;激 振器產生的激振力設為30N，得到大幅激振力時，無阻尼器及有阻尼器拉索模型強迫振動面內前五階振 幅-激振頻率關系的比較如圖9所示.其余各階結果在表5中列出.

在小幅激振力作用下，有阻尼器拉索模型一至五階強迫振動的共振頻率均比無阻尼器拉索模型的自振頻率略大.無阻尼器和安裝摩擦阻尼器后，一至五階共振幅值如表5所示，一至五階共振幅值分別減小了24.26%、16.79%、9.16%、58.37%、11.46%.在安裝摩擦阻尼器后，一至五階共振頻率均有增大的趨勢，隨著階數增加，共振頻率增大更明顯.

在大幅激振力作用下，有阻尼器拉索模型一至五階強迫振動的共振頻率同樣比無阻尼器拉索模型的自振頻率略大.無阻尼器和安裝摩擦阻尼器后，一至五階共振幅值如表5所示，一至五階共振幅值分別減小了53.44%、46.99%、77.33%、82.20%、62.97%，與一、二階相比，摩擦阻尼器可更加有效地抑制三、四、五階強迫振動.安裝摩擦阻尼器后前五階共振頻率均有增大的趨勢，高階共振頻率增大幅度比一階共振頻率增大幅度更大.

綜合圖8、圖9及表5可得結論如下：摩擦阻尼器可以有效減小拉索在小幅與大幅激振力作用下的前 五階共振幅值，并可以更加有效地抑制拉索大幅強 迫振動.不論小幅還是大幅強迫振動，安裝摩擦阻尼器后，一至五階的強迫振動共振頻率均比自由索模型的自振頻率略大.

5? 結語

通過以上試驗及分析可以得出如下結論：

1）摩擦阻尼器用于拉索減振，存在工作與鎖住兩種工作狀態.摩擦阻尼器工作時拉索振幅近似線 性衰減，當摩擦阻尼器鎖住并停止工作后，由于拉索內阻尼極小，振動衰減極慢.由此可知，系統對數衰減率的最大值與振幅相關，當振幅較小時，摩擦阻尼器不工作，對數衰減率幾乎為0;隨著振幅逐漸增大，對數衰減率逐漸增大并取得最大值;隨著振幅繼續增大，對數衰減率又開始逐漸減小.

2）對數衰減率-振幅曲線隨著摩擦力的增大向振幅增大的方向平移，其一階最大對數衰減率基本 不變，臨界工作振幅及最大對數衰減率對應的振幅 逐漸增大，摩擦力越大，對數衰減率-振幅曲線下降段越平緩.

3）摩擦阻尼器-拉索系統在自由衰減振動過程中頻率緩慢增大;當摩擦阻尼器由工作狀態轉換為鎖住狀態時，系統的自振頻率有小幅度突增.

4）摩擦阻尼器可以有效減小不同幅值激振力作用時強迫振動的共振幅值，并且對大幅激振的減振效果更明顯.在大幅激振力作用下，摩擦阻尼器可使 拉索前五階共振幅值減小53.44%～82.20%;階數越高，摩擦阻尼器對共振幅值的減小幅度越大.

摩擦阻尼器在工作時，可以為拉索系統提供較大的阻尼比;當拉索振動幅值比較小時，摩擦阻尼器不工作可以減少阻尼器的磨損.目前摩擦阻尼器在國外實際工程中已得到了一定的推廣應用，在國內已應用于萬州長江公路三橋.

參考文獻

[1]顧安邦，向中富.橋梁工程：下冊[M].北京：人民交通出版社，2012：285-286.

GU A B，XIANG Z F.Bridge engineering：vol.2 [M].Beijing： China Communications Press，2012：285-286.（In Chinese）

[2]李國強，顧明，孫利民.拉索振動、動力檢測與振動控制理論[M].北京：科學出版社，2014.

LI G Q，GU M，SUN L M.Theory of cable vibration，dynamic de-tection and vibration control[M].Beijing：Science Press，2014.（In Chinese）

[3]周海俊，孫利民，時晨.摩擦型阻尼器的斜拉索減振試驗研究[J].同濟大學學報（自然科學版），2006，34（7）：864-868.??? ZHOU H J，SUN L M，SHI C.A full-scale experimental study on cable vibration mitigation with friction damper [J].Journal of Tongji University（Natural Science），2006，34（7）：864-868.（In Chinese）

[4]GAO D L，CHEN W L，ZHANG R T，et al.Multi-modal vortex-and rain-wind-induced vibrations of an inclined flexible cable[J].Mechanical Systems and Signal Processing，2019，118： 245-258.

[5]陳文禮，陳冠斌，黃業偉，等.斜拉索渦激振動的被動自吸吹氣流動控制[J].中國公路學報，2019，32（10）：222-229.

CHEN W L，CHEN G B，HUANG Y W，et al.Vortex-induced vi-bration control of a stay cable based on the passive-suction-jet method[J].China Journal of Highway and Transport，2019，32（10）：222-229.（In Chinese）

[6]李壽英，李振宇，陳政清.黏滯慣性質量阻尼器對斜拉索減振效果的數值分析[J].中國公路學報，2019，32（10）：230-236.LI S Y，LI Z Y，CHEN Z Q.Numerical analysis on the effective-ness of viscous inertial mass dampers on stay cables of cable-stayed bridges [J].China Journal of Highway and Transport，2019，32（10）：230-236.（In Chinese）

[7]劉慶寬 .斜拉索風雨振研究現狀和尚待解決的問題[J].石家莊鐵道大學學報（自然科學版），2010，23（2）：53-58.

LIU Q K.Review of present research and problems to be solved of rain-wind induced vibration of cables[J].Journal of Shijia-zhuang Tiedao University（Natural Science），2010，23（2）：53-58.（In Chinese）

[8]LI S Y，WU T，LI S K，et al.Numerical study on the mitigation of

rain-wind induced vibrations of stay cables with dampers [J].Wind and Structures，2016，23（6）：615-639.

[9]何旭輝，陳政清，黃萬林，等.MR阻尼器在抑制斜拉橋拉索風雨振中的應用研究[J].湖南大學學報（自然科學版），2002，29（3）：91-95.

HE X H，CHEN Z Q，HUANG W L，et al.Application of MR dampers in rain-wind-induced vibration control of cable-stayed bridge [J].Journal of Hunan University（Natural Sciences），2002，29（3）：91-95.（In Chinese）

[10]CHEN L，SUN L M.Steady-state analysis of cable with nonlinear

damper via harmonic balance method for maximizing damping[J].Journal of Structural Engineering，2017，143（2）：04016172.

[11]MAIN J A，JONES N P.Free vibrations of taut cable with at-tached damper.II：nonlinear damper[J].Journal of Engineering Mechanics，2002，128（10）：1072-1081.

[12]SUN L M，CHEN L.Periodic responses of a taut cable attached

with a friction damper computed using multi-harmonic balance method [C]//IABSE Conference，Guangzhou 2016：Bridges and Structures Sustainability-Seeking Intelligent Solutions.May8-11，2016.Guangzhou，China.Zurich，Switzerland：International Association for Bridge and Structural Engineering（IABSE），2016：464-471.

[13]CLOUGH R W，PENZIEN J.Dynamics of structures[M].3rd ed.Berkeley，California，USA：Computers and Structures Inc，2003.

[14]WARNITCHAI P.Nonlinear vibration and active control of cable-stayed bridges[D].Tokyo：University of Tokyo，1990.

[15]MAIN J A，JONES N P.Analytical investigation of the perfor-mance of a damper with a friction threshold for stay-cable vibra-tion suppression[C]//Proceedings of15th ASCE Engineering Me-chanics Conference.New York：Columbia University，2002.

[16]XU Y L，ZHAN S N，KO J M，et al.Experimental study of vibra-tion mitigation of bridge stay cables[J].Journal of Structural Engi-neering，1999，125（9）：977-986.