核心素養視角下高中數學建模的教學探索

楊曉芳

【摘?要】??高中數學教學的過程就是培養學生核心素養的過程，就是促進學生全面發展的過程.教師要具體的教學中要以學生為中心，著力提升他們的能力，促進他們的素養，而不能只關注最終的成績.《普通高中數學課程標準》（2017年版）指出，高中數學學科的核心素養包括數學抽象、邏輯推理、數學建模等.數學建模就是教師引導學生將實際問題變為用數學語言描述的數學問題的過程.函數應用問題是高中數學學習的重點也是難點，學生往往不能舉一反三、觸類旁通.教師可引導學生建立數學模型，進而促成此類問題的解決.

【關鍵詞】??高中數學;核心素養;數學建模

一般來說，運用數學建模解決函數應用問題通常分為四步，首先為讀題，就是要能讀出里面的數學問題來，要能讀出里面的條件與結論，進而再理清里面的數量關系.其次為建模，就是要將情境中的文字轉化為數學語言，進而建立相應的函數模型.第三步為求解，就是求解函數模型，從而得到數學結論，最主要的，學生要能關注函數模型中元素的實際意義.最后一步為回答，就是學生要對建模后獲得的數學結論進行還原，從而給出實際問題的結果.整個建模的過程就是學生開啟思維、自主創造，進而解決問題的過程??[1] .

1?創設現實情境，讀出數量關系

建模的目的是為了解決問題，要培養學生建模的能力，教師首先要創設真實的情境，讓他們去讀懂情境中蘊含的數學問題??[ ??2???] .當前部分高中學生解題能力不強，其中一個重要的原因就是讀題能力差，不能抓住題目中的關鍵信息，讀不出其中蘊含的數量關系.因此教師要依據學生的基本學情，設置他們容易找出數量關系的貼近他們生活的情境.

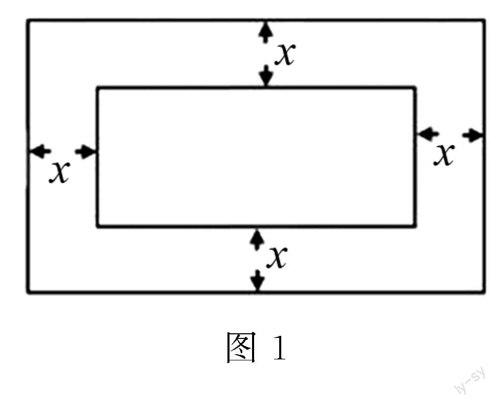
例如???某學校要在長為8米，寬為6米的一塊矩形地面上進行綠化，計劃四周種花卉，花卉帶的寬度相同，均為x米，中間植草坪.為了美觀，要求草坪的面積大于矩形土地面積的一半，則x的取值范圍是多少？對于這樣的文字題，學生最要緊的一步就是依照文字，畫出圖形，在圖形中標出相關的信息.換言之，讀題的第一步就是要指導學生進行思維的轉換，以簡潔的圖形表達原題.

學生畫出圖1，并標出花卉帶的寬度x.接著教師引導學生找出這個圖中涉及到的兩個量，即中間草坪的長與寬，讓他們嘗試著用自己的語言描述這兩個量之間的關系.學生發現這兩個量均可以通過x來表示，原題中設花卉帶寬度為x米（0?1?2?×8×6.可以看出來.只有放手給學生不斷實踐的機會，學生的建模能力才能得到有效提升.

2?分析主要因素，建立函數模型

建模的第二步就是要指導學生選擇合適的函數模型來刻畫已經確立的具體對象的數量變化關系??[ ??3???] .學生可根據題目提供的數據先畫出它的圖像，從直觀上看看像什么函數.教師可指導學生說一說學過一些什么函數，以讓他們回顧一下一次函數、二次函數、反比例函數、指數函數、對數函數、分段函數等，進而確立最終的建模函數.學生回顧之后，教師可追問眼前的這個圖像最像什么函數的圖像，能大概寫出它的解析式嗎.也就是說建模的過程是學生主動找尋函數解決問題的過程，使他們提升數學素養的過程.

例如???某海濱浴場一天的海浪高度y?m?是時間t?0≤t≤24??h?的函數，記作y=f?t?，圖2是某天各時的浪高數據.

題目中給出的是海濱浴場的海浪高度y?m?與時間t?h?的數量關系，學生首先要弄清楚的就是能不能選用一個三角函數來描述這個關系.他們以時間為橫坐標，海浪高度為縱坐標，將圖2的數據帶進去，于是在平面直角坐標系中就出現如圖3所示的散點圖.

依據圖3，學生認為可以選用函數y=A?sin??ωt+φ?+h?A>0，ω>0，?φ?≤??π??2??來近似描述這個海濱浴場的海浪高度y?m?與時間t?h?的函數關系.教師將學生分成不同的小組，讓他們展開討論，他們先是從表中數據和散點圖中獲得A=?1.5-0.5?2?=?1?2?，T=12，所以?2?π??ω?=12，得ω=??π??6?.接著他們又從h=?1.5+0.5?2?=1，得出y=?1?2??sin????π??6?t+φ?+1.對著圖，學生發現??π??6?×0+φ=??π??2?+2k?π?，k∈?Z?.又因為?φ?≤??π??2?，所以φ=??π??2?，所以y=?1?2??sin????π??6?t+??π??2??+1，即y=??1?2??cos???π??6?t?+1?0≤t≤24?.在這個建模的過程中，教師要遵循針對性原則，就是要對個別的學生強化輔導，要讓他們的思維跟上課堂的節奏.

3?關注實際意義，運用函數模型

對高中數學學習而言，教師需要培養學生的運用能力，即，將認知轉化為數學素養的能力.一般來說，教師在教學的過程中可以開展以下活動，一是學習理解類活動，就函數而言，就是要能理解不同函數的圖像、性質等.二是要開展實際應用與遷移創新類活動，就函數建模而言，就是要能將建立的模型運用起來，以解決實際的問題.

學生依據圖3，建構這樣的函數模型，y=??1?2??cos???π??6?t?+1?0≤t≤24?.教師說，當海浪高度不少于1m時才對沖浪愛好者開放海濱浴場，能不能依據建構的模型判斷一天內的8h至20h之間，有多少時間可供沖浪愛好者進行沖浪？通過這樣的設問，教師最重要的目的，就是讓他們繼續思考下去，讓他們的深度學習開展下去.在數學建模的過程中，教師要引導學生全面地思考，不但要讓他們學會析模與用模.對于運用環節，教師關注的不只是最后的結果，教師要看到他們的思考和交流.

因此教師可開展小組合作的模式，引導學生展示自己思考和探究的過程，鼓勵他們之間進行交流和討論.學生在討論中將條件一一利用，他們根據海浪高度不少于1m 時，得出y≥1，進而得出??1?2??cos???π??6?t?+1≥1，換言之，?cos???π??6?t≥0.接著他們在合作中推出這樣的式子2k?π?-??π??2?≤??π??6?t≤2k?π?+??π??2??k∈?Z??，即12k-3≤t≤12k+3?k∈?Z??.學生在合作中分析問題、解決問題，他們在數學建模的過程中，提升運用數模的能力.最后，他們加上這樣的條件0≤t≤24，得出0≤t≤3或者9≤t≤15或者21≤t≤24.也就是說一天內的8h至20h之間有6h可供沖浪愛好者進行沖浪.

4?還原數學結論，檢驗相應模型

建模中還有一個重要的環節，就是要學會將“模”與現實的題目結合起來，進而得出正確的結論，同時要驗證“模”的可行性.對于高中學生來說，他們有時候在確立了函數的模之后，卻不能依照實際的情況，對可能不存在的結論進行取舍.因此教師要培養學生依照實際情況分析的能力??[ ??4???] ，要提升他們的綜合素養.一般來說，學生在建模之后，基本能將新的數值帶進去，獲得新的結論.但是現實的情況是變化的，學生要學會變通，要能抓住關鍵的信息進行合理的推斷.

例如????倫敦有一個32個乘坐艙的景觀摩天輪如圖4所示，每相鄰兩個乘坐艙與旋轉中心所成的圓心角均相等，乘坐艙按旋轉順序依次為1～33號，因宗教忌諱，沒有13號.乘客在乘坐艙距離地面最近時進入，t ?min?后他們距離地面的高度為：

f（t）=A?sin?（ωt+φ）+B（A>0，ω>0，φ∈（0，2?π?）），天輪的旋轉半徑為60m，最高點距地面135?m?，旋轉一周大約30?min?.現有甲乘客乘坐11號乘坐艙，當甲乘坐摩天輪15?min?時，乙距離地面的高度為（75+30?2?）m，則乙所乘坐的艙號為多少.

學生首先要運用給出的函數求出摩天輪的最低點離地面的距離，因最高點距地面為135?m?，依據?f?（t）????max???=A+B=135，摩天輪的旋轉半徑為60?m?，那么最低點距地面135-2×60=15（?m?）.學生進一步推測出f?（t）????min??=-A+B=15，進而他們求得A=60，B=75;又因為摩天輪旋轉一周大約30?min?，他們求得周期T=?2?π??ω?=30，解得ω=??π??15?.他們再進一步地利用函數f?t?=60?sin?（??π??15?t+φ）+75，因為f（0）=60?sin?φ+75=15，所以?sin?φ=-1，又φ∈（0，2?π?），于是有φ=?3?π??2?.再進一步地他們得出f?t?=60?sin?（??π??15?t+?3?π??2?）+75=-60?cos???π??15?t+75，t∈[0，30]，令f（t）=75+30?2?，解得t=?45?4?或t=?75?4?.當學生做到這一步時，他們需要跳出所建立的模，回到原先的題目中去.也就是說要將函數中獲得的結論轉化為最終情境所需要的答案.學生由每相鄰兩個乘坐艙與旋轉中心所成的圓心角?2?π??32?=??π??16?，得出后一個乘坐艙轉到相鄰前一個乘坐艙位置用時???π??16????π??15??=?15?16?（?min?）.顯然地，當t=?45?4??min?時，乙比甲晚出發15-?45?4?=?15?4?（?min?），甲乙相差??15?4???15?16??=4個乘坐艙.再次，學生需要抓住原情境的信息做出選擇.由于沒有13號，此時乙在16號乘坐艙;當t=?75?4??min?時，乙比甲早出發?75?4?-15=?15?4?（?min?），甲乙相差??15?4???15?16??=4個乘坐艙，此時乙在7號乘坐艙.最后他們得出乙所乘坐的艙號為7或16.可見教師要引導學生將函數模型的分析內容反映至實際對象，進一步修正模型的適用性，從而提升學生的解題能力.

5?結語

教師在數學教學的過程中，要基于核心素養優化教學環節.數學建模能促進學生核心素養的發展，因為在建模的過程中學生的推理思維和發散思維獲得充分的鍛煉.這些高階思維能力在建模的實踐過程中逐步形成創新意識，從而提升學生的綜合素養.所以在建模的實踐活動中，教師要關注學生的內在訴求.幫助他們建立正確的建模習慣.同時教師也要充分準備，精選問題，創設情境為學生帶來全新的建模體驗，進而促成數學核心素養的生長.

【基金：本論文系《核心素養視角下高中數學建模的教學實踐研究》課題研究成果.立項號：2021JY14-L56.】

參考文獻：

[1] 陳亮.基于核心素養培養的高中數學建模教學探討[J]廣西教育，2020（46）：140-141

[2]范東暉.核心素養視域下的高中數學建模教學——以“停車距離問題”的教學為例[J]中國數學教育，2021（10）：28-31

[3]饒真平.新課標下的高中數學建模暢想[J]數學大世界（下旬），2019（09）：85

[4]李思聰，張仕橙.注重建模思維引領，培養數學核心素養[J]數學教學通訊，2019（18）：20-21