非線性能量阱振動抑制效果理論分析與試驗研究

樓京俊，李 爽，柴 凱，盧錦芳

(1. 海軍工程大學艦船與海洋學院，武漢 430033；2. 海軍工程大學動力工程學院，武漢 430033)

潛艇機械設備大多采用直流幅壓電機驅動，當蓄電池電壓或外界激勵特性變化時，其周期性運轉產生的線譜頻率存在波動效應，呈現寬頻線譜特征，導致艇用線性動力吸振器(Tuned vibration absorber, TVA)吸振效率難以達到理想效果，進而影響聲隱身性能。非線性能量阱(Nonlinear energy sink, NES)通常指具有本質非線性剛度的被動動力吸振裝置，與傳統TVA 相比，具有輕質、減振頻帶寬、魯棒性強等優點。近些年，該技術在航空航天[1]、房屋橋梁抗震[2-3]、能量采集[4]以及結構聲學控制[5]等領域得到了廣泛應用。但目前NES 技術在潛艇乃至船舶減振降噪領域的應用鮮有報道。

國內外學者對利用NES 抑制結構穩態振動一直較為關注。Jiang 等[6]指出在正弦激勵下，NES能夠在較寬頻帶內從線性振子吸收能量，并證明不管前向還是后向掃頻，NES 都能實現能量定向傳遞(Targeted energy transfer, TET)。Wagg 等[7]研究了主結構受正弦周期力時受約束多自由度碰撞非線性系統的能量傳遞問題，指出當激勵幅值達到一定閾值時，能量會向NES 振子積聚，而且根據激勵幅值不同系統會出現周期、弱調制、強調制 3 種響應形式。Starosvetsky 等[8]通過相軌跡法給出了三種響應類型與系統平衡點關系，指出系統慢變方程對應周期解是否分岔是NES 實現TET的關鍵。文獻[9]構造了等價的電路圖，通過電路實驗觀察到了NES 系統的強調制響應現象。陳東陽等[10]通過遺傳算法對NES 裝置結構參數進行了優化設計，有效抑制了柱體結構的渦激振動。劉艮等[11]對等效梁附加NES 的桁架結構進行瞬態減振研究，分析了懸掛位置、NES 質量等對性能的影響，結果表明NES 被動減振效果明顯優于線性剛度阻尼減振器。譚平等[12]開展了NES 減振系統受基底簡諧激勵的分岔特性分析，筆者在此基礎上采用柔性鉸鏈結構[13]提出了一種NES 構造方法，并用復變量平均法分析了簡諧激勵下耦合系統的局部分岔特性。

上述研究偏重于減振機理分析，實驗成果較少，且理論分析模型中NES 結構與主系統大多采用橫向布置的耦合方式，存在摩擦阻尼大以及附加質量重力效應等問題，對抑制大型機械設備垂向振動工程實用性不強，亟需開發一種剛度可調、結構緊湊、兼具一定垂向承載能力的NES 裝置。

另外，NES 系統屬于強非線性系統，諧波平衡法聯合Newton-Raphson 迭代是分析該類系統周期解的有利手段[14]，但在分岔點處，由于雅克比奇異，迭代過程會遇到局部不收斂問題，難以實現對解響應的完整追蹤，從而無法得到周期解的分岔信息與系統真實響應。Zang 等[15]提出了一種擬弧長延拓法，用于追蹤系統幅頻特性曲線，該法能有效通過分岔點，但在共振點附近計算效率有待提高。

基于上述分析，本文提出利用增量諧波平衡法(Incremental harmonic balance method, IHB)結合弧長延拓法求解NES 系統周期解，基于Floquet穩定性理論對周期解穩定性進行判別，從而構建起非線性能量阱系統周期解的完整圖像。并以該理論為基礎，開展結構參數對NES 振動抑制效果影響研究以及結構參數優化設計研究。另外，在文獻[13]的基礎上，本文研制了一種可垂向承載的柔性鉸鏈型NES 原理樣機，并開展了相關試驗，有效驗證了理論分析成果，對于深入理解NES系統動力學特性、豐富NES 結構設計以及推動NES 技術在船舶減振降噪領域發展均具有一定的指導意義。

1 動力學建模

系統運動學模型如圖1 所示。

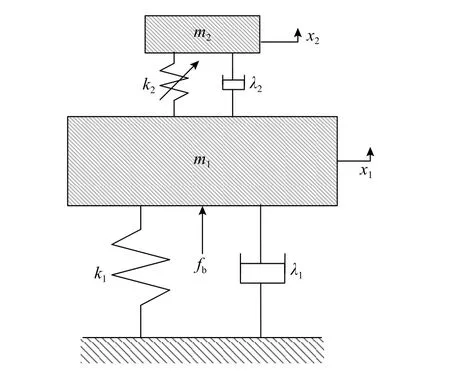
圖1 機械設備耦合NES 的吸振系統動力學模型Fig. 1 Dynamical model of absorption system coupled with a NES

圖1 中，m1為待減振機械設備，通過線性剛度 彈 簧k1、阻 尼λ1與 剛 性 基 座 連 接；未 接 地NES 由質量m2、非線性剛度k2及阻尼λ2構成，并與機械設備上層耦合相連。fb為外界激勵信號集中作用于機械設備下表面中心點，滿足fb=FcosΩt；x1、x2分別為機械設備與NES 垂向位移。且本文所研究NES 的力-位移關系滿足fNES=k2(x2-x1)3。

根據牛頓第二定律，系統運動學方程為：

2 周期解計算方法

2.1 增量諧波平衡法

2.2 弧長延拓法

2.3 周期軌道的穩定性

2.4 算法驗證

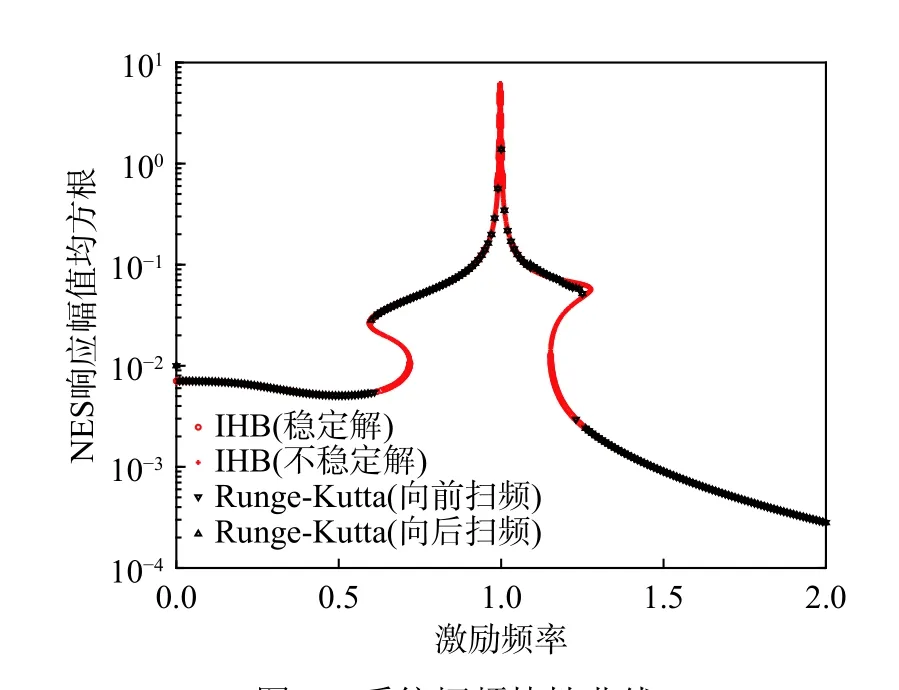
圖2 系統幅頻特性曲線Fig. 2 The frequency-amplitude response curve

3 結論振動抑制效果分析

3.1 評價指標選取

3.2 阻尼對振動抑制效果的影響分析

固 定 參 數 ε=0.05 、 β=0.5 、 ξ1=1.2×10-3、f=0.01，不同阻尼下主系統振動能量曲線如圖3所示。從圖中可知，當未耦合NES 時，系統在ω=1 處 存在一根明顯共振峰。當 ξ2=0.012時，能量曲線存在一段扭曲環狀不穩定解，導致在1.037≤ω≤1.045范圍振動能量高于未耦合NES的工況，NES 不僅無法起到振動抑制效果，反而會惡化機械設備振動。當 ξ2=0.02時，該扭曲環狀曲線消失，并融合成一整段不穩定解，此時系統分岔點為0.9806 和1.025，在分岔點之間NES 都具備較好的振動抑制效果。而當 ξ2=0.05 和ξ2=0.12時，能量曲線中不穩定周期解消失，系統響應趨近于線性特征，進而在新的共振頻率附近呈現單一共振峰。此外，圖中 ξ2=0.05時共振頻率為0.9852，共振能量為0.0374，而 ξ2=0.12時共振頻率為0.9781，共振能量為0.1376。因此，大阻尼不僅使耦合系統共振頻率左移，且會導致機械設備振動能量增加。

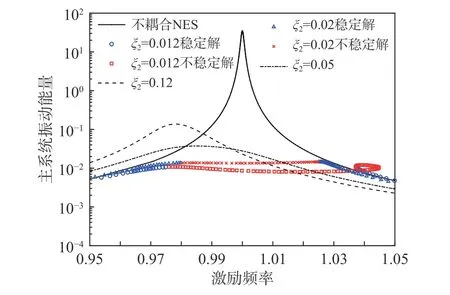
圖3 阻尼對振動抑制效果的影響Fig. 3 The influence of NES damping to the vibration suppressing performance

因此，本文主要在 ξ2=0.02的弱阻尼條件下，進一步分析質量比和非線性剛度對NES 振動抑制效果的影響。

3.3 理論分析

選取參數 ξ1=0.0012 、 ξ2=0.02 、 β=0.5、f=0.01，不同質量比下主系統振動能量曲線如圖4 所示。從圖4(a)可知，當 ε=0.167時，能量曲線中同樣存在一段扭曲的不穩定解；當 ε=0.083時，該扭曲曲線退化形成一整段平緩的不穩定解；若進一步減小質量比，共振頻率附近的不穩定解區域逐漸拓寬，主系統振動能量持續降低，從而使NES 具備了更強的寬頻振動抑制效果。

從圖4(b)可知，當 ε=0.033時，能量曲線開始分裂出多段不穩定分枝，同時系統最大振動能量開始增加；當 ε=0.02時，能量曲線中不穩定解消失，系統呈線性特征，進而產生新的單一共振頻率，該共振頻率逐漸向主系統固有頻率靠攏，共振峰值也隨之增加，表明振動抑制效果開始下降。因此，在弱阻尼條件下NES 存在最優質量比。

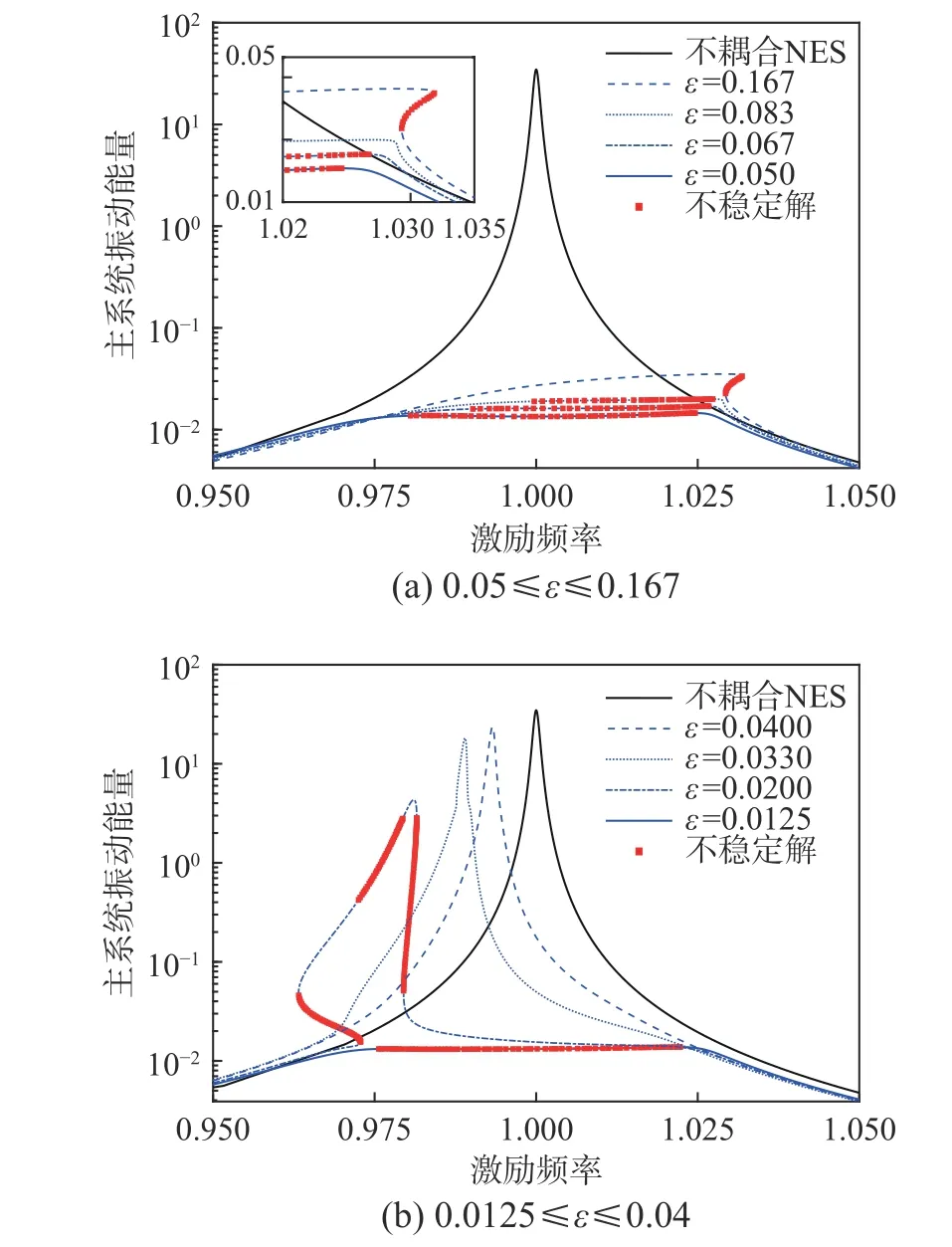
圖4 質量比對振動抑制效果的影響Fig. 4 The influence of mass ratio to the vibration suppressing performance

3.4 剛度對振動抑制效果的影響分析

選 取 參 數 ε=0.05 、 ξ1=0.0012 、 ξ2=0.02、f=0.01，不同剛度下主系統振動能量曲線如圖5 所示。從圖5(a)可知，當剛度為0.0625 和0.125 時，系統線性特征明顯，共振峰能量隨剛度增大逐漸減小，當剛度增大到0.25、0.5 以及1 時，能量曲線開始出現不穩定解，不穩定解區間隨剛度增加逐漸拓寬，振動能量幅值也逐漸減小，表明此時NES 在共振頻率附近的寬頻吸振效果隨剛度增加逐漸得到加強。從圖5(b)可知，當剛度再次增大時，能量曲線會變得異常復雜，且再次產生明顯共振峰，當 β=2時新共振峰能量已接近沒有耦合NES 時的共振峰能量，已完全不具備共振峰抑制能力。因此，在弱阻尼條件下NES同樣存在最優剛度。

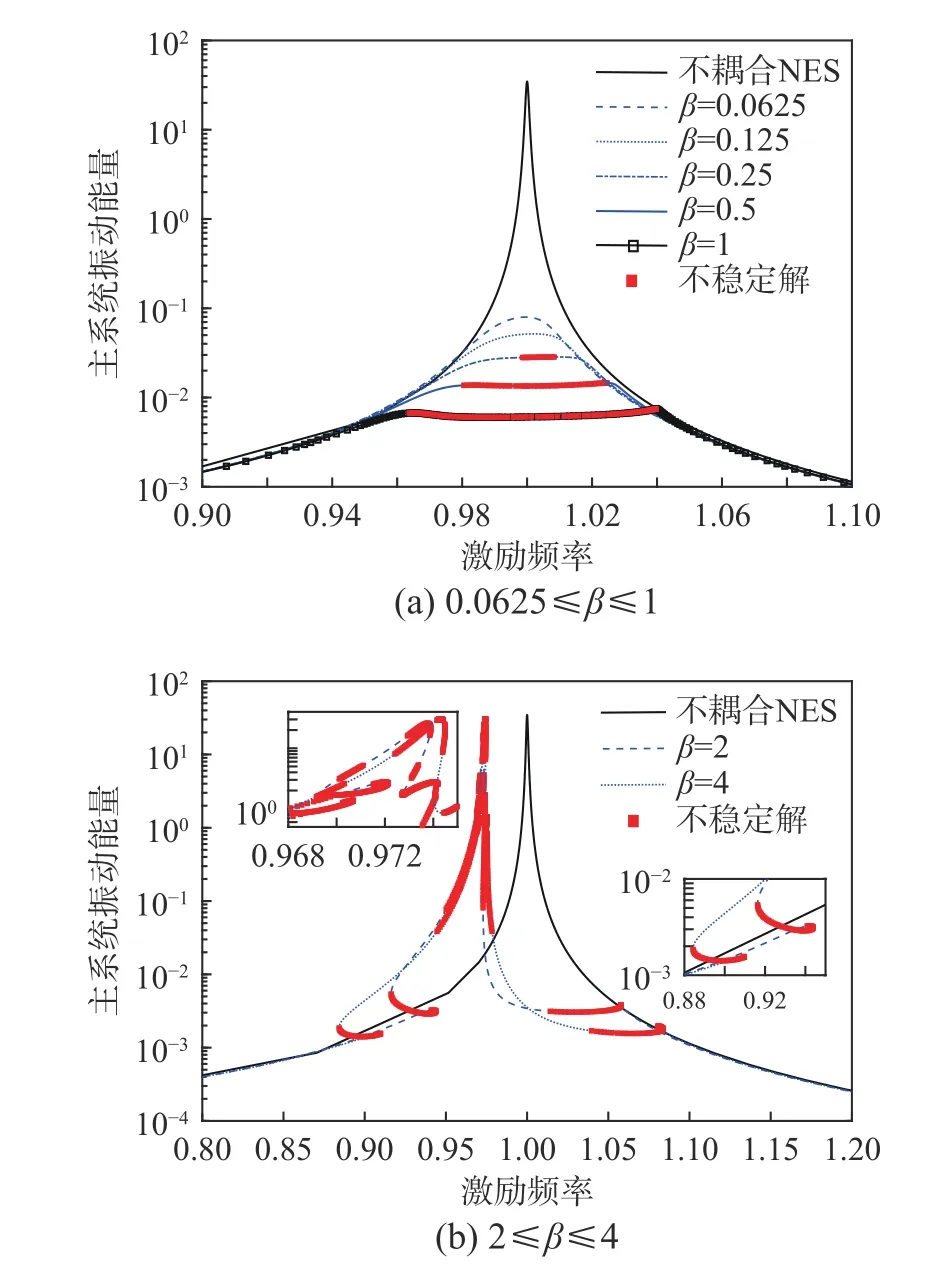
圖5 剛度對振動抑制效果的影響Fig. 5 The influence of NES stiffness to the vibration suppressing performance

4 結論參數優化與魯棒性研究

4.1 結構參數優化

質量、剛度以及阻尼是設計NES 的三個關鍵參數，由前文分析可知，NES 振動抑制效果隨三個參數都是非線性變化的。固定質量比 ε=0.05不變，本節采用局部優化算法進一步確定NES 最優阻尼和剛度。其中優化變量以及變化區間設定為：

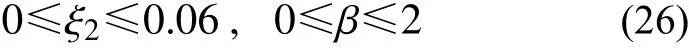
優化目標設定為共振頻率附近主系統最大振動能量最小，優化函數為：

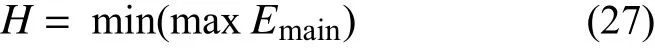
由于上述優化函數沒有明確的解析表達式，本文采用Runge-Kutta 法結合枚舉法直接局部尋優求解。其中初始條件均設置為0，外界激勵頻率變化為 0.8≤ω≤1.2 ， 頻率間隔取0.01， ξ2間隔取0.0025， β間隔取0.025。主系統最大振動能量三維圖和在 (ξ2,β)平面投影的二維等高線圖如圖6所示。

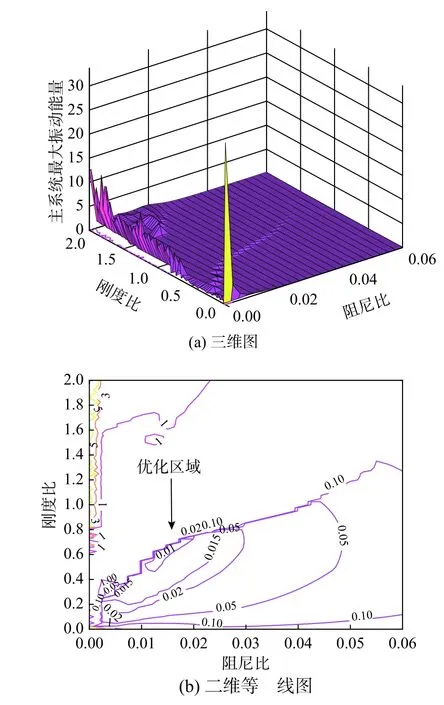
圖6 NES 剛度和阻尼參數優化結果Fig. 6 The parameters optimization results of the NES stiffness and damping

從圖6 可知，沒有耦合NES 時主系統最大振動能量為33.68，而耦合NES 后在大部分參數范圍內，最大振動能量均得到了大幅度的衰弱，優化參數位于振動能量為0.008 的等高線內，若以此區域內的參數設計NES，主系統最大振動能量衰減效率則達到了99.98%。除此之外，該優化區域主要集中 0.006≤ξ2≤0.025的弱阻尼范圍之內，這與前文分析結果一致。另外，圖中存在一條最大振動能量為0.05 的明顯分界線，這意味著剛度參數向上偏離該優化區域時，NES 振動抑制效果會陡然降低，因此相較阻尼而言，NES 振動抑制效果隨剛度參數變化更加敏感。若在優化區域內選擇參數 ε=0.05 、 ξ2=0.02 、 β=1.15，機械設備振動響應如圖7 所示。從圖中可知，此時機械設備處于準周期運動狀態，確切來說是一種強調制響應，文獻[7]指出這是由于對應慢變系統極限環的鞍結分岔引起的。

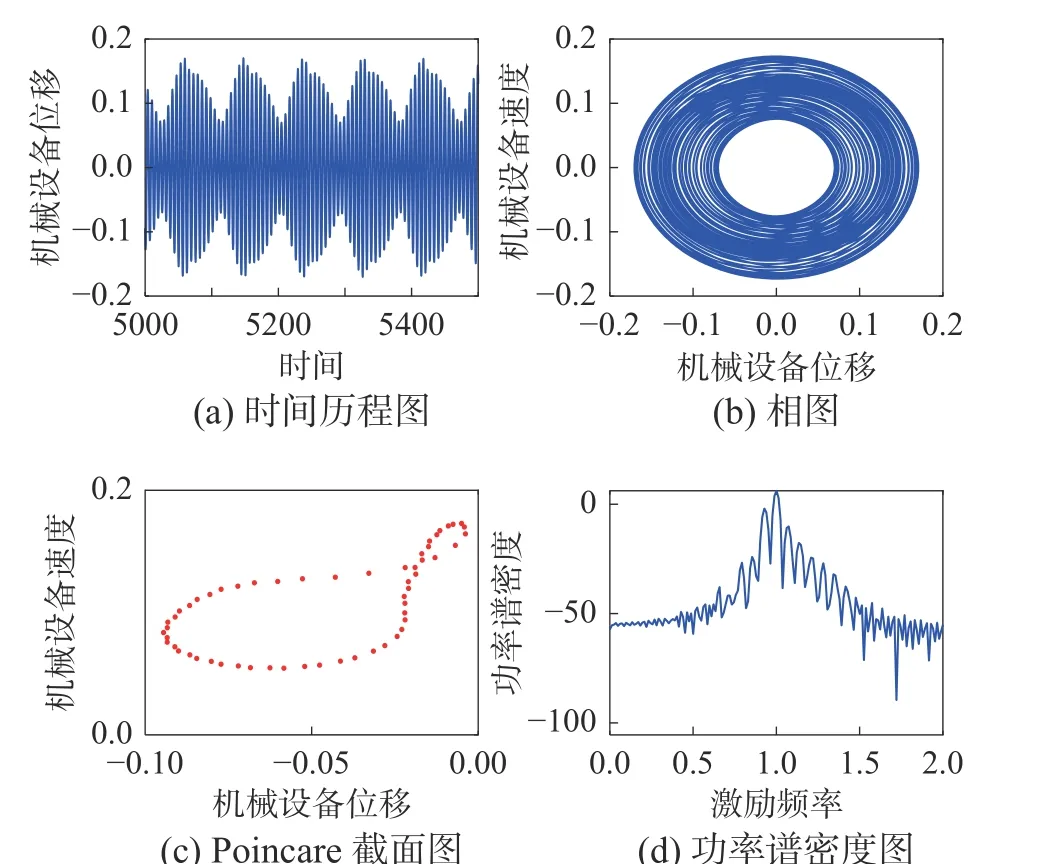
圖7 機械設備振動響應Fig. 7 The system vibration response of mechanical equipment

4.2 魯棒性分析

進一步選取參數 ε =0.05 、 ξ2=0.02 、 β =1.15，考察外界激勵頻率在中心共振頻率1 的 ±20%范圍，而激勵幅值在0.01 的 ±50%范圍內變化時的NES 振動抑制效果，計算結果如圖8 所示。

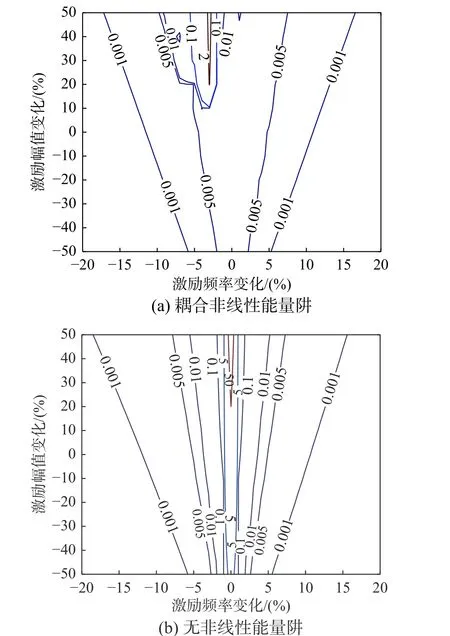
圖8 系統最大振動能量隨外界激勵變化的二維等高線圖Fig. 8 Contour plot of the max vibration energy of the system versus excitation frequency and amplitude

從圖中可知，當激勵頻率變化時，與沒有耦合NES 相比，NES 一直能保持較好的振動能量衰減效率；而當激勵幅值變化時，等高線對應的系統最大振動能量與圖6(b)中優化區域有明顯提升，但這主要是由于外界輸入能量增大引起的，此時NES 能量衰減效率也接近98%。因此，對于優化后的NES 結構參數，當外界激勵頻率和激勵幅值在一定范圍內變化時，仍具有良好的振動抑制效果，這體現了NES 的寬頻吸振優勢以及較好的魯棒性。

5 實驗研究

為了滿足潛艇機械設備垂向振動減振需求，筆者前期基于正負剛度并聯原理，利用雙開槽柔性鉸鏈與線性螺旋彈簧并聯設計了一種可垂向承載的立方剛度NES 結構，如圖9 所示。力學特性具體推導過程可參考文獻[13]。

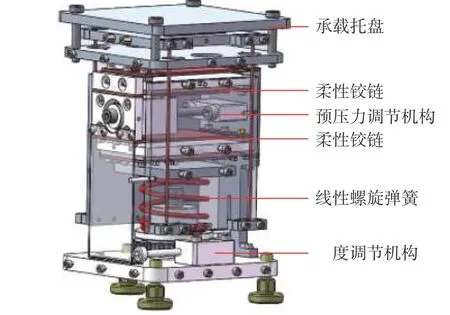
圖9 柔性鉸鏈型NES 結構三維圖Fig. 9 The 3D drawing of the proposed NES apparatus constituted by flexible hinges

具體結構參數如表1、表2 所列。

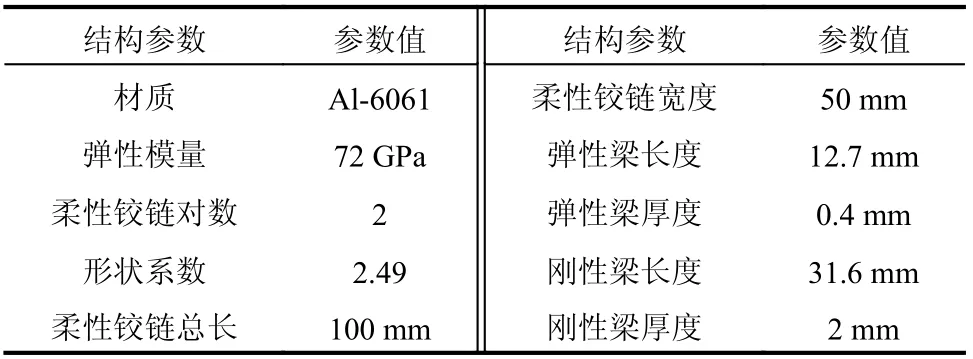
表1 柔性鉸鏈主要結構參數Table 1 The main structural parameters of the flexible hinges

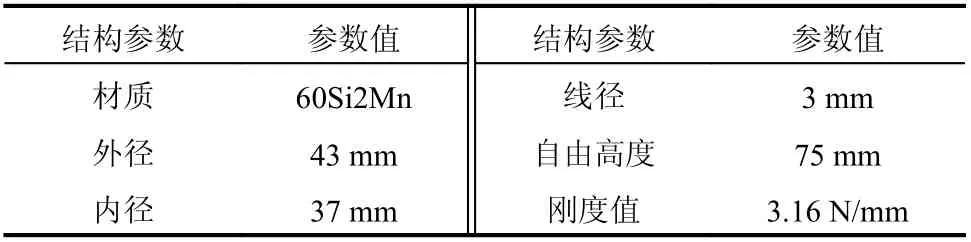
表2 垂直螺旋彈簧參數Table 2 The main parameters of vertical linear spring

此外，預壓力水平調節彈簧剛度為58.7 N/mm。在臨界預壓力條件下通過靜態壓縮試驗測得柔性鉸鏈型NES 結構力-位移曲線如圖10 所示。

由圖10 可知，通過對試驗數據進行3 次多項式擬合，所設計NES 結構靜剛度擬合值與理論值吻合良好，并呈現立方剛度特性，具體值為0.052 N/mm3。基于德國M+P 公司VibMobile 振動測試平臺，進一步開展NES 動態性能測試試驗，試驗原理圖以及測試現場照片如圖11 和圖12 所示。

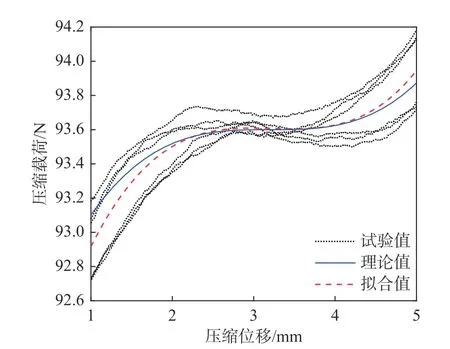
圖10 柔性鉸鏈型NES 結構靜剛度測試結果Fig. 10 The static stiffness of the proposed NES apparatus

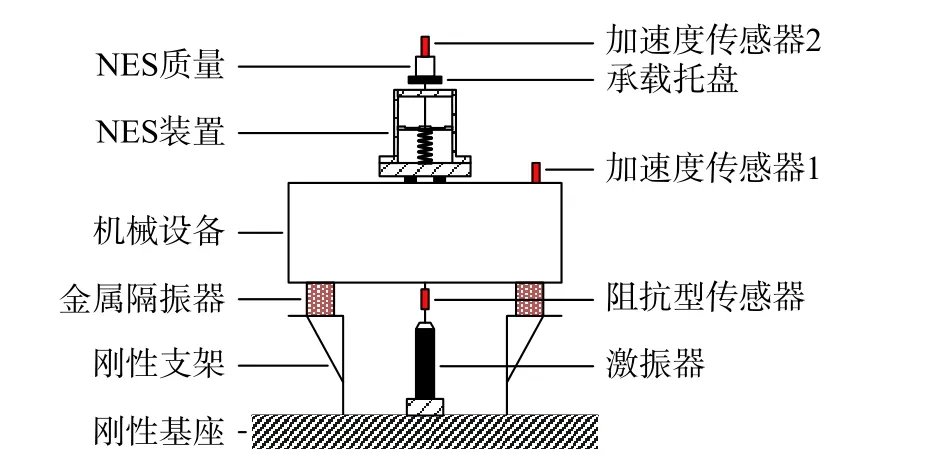
圖11 試驗原理圖Fig. 11 The block diagram of the test

圖12 測試現場Fig. 12 The test spot

其中主系統由單層隔振平臺代替，均勻分布的質量塊模擬機械設備，對稱放置于4 個金屬隔振器上；激振器固定在基座上，并通過風機散熱，其輸出端布置1 個阻抗型傳感器，通過導桿與機械設備下表面中心點連接，阻抗型傳感器可同時測量激振器的輸入力信號與加速度信號；機械設備上表面中心點布置NES 裝置，機械設備與NES 質量塊上表面各布置1 個加速度傳感器，并在兩者之間布置1 個磁阻尼器，用于調節NES 結構的阻尼；此外，VibMobile 振動測試系統的信號源輸出端通過功率放大器與激振器連接，數據采集端口與各傳感器連接，從而構成測試系統閉環。系統主要參數如表3 所列。

表3 測試系統主要參數Table 3 The main parameters of test system

試驗過程中采用對數掃頻，掃頻范圍為1 Hz～100 Hz，掃頻速度為1 oct/min，采樣頻率為2048 Hz，數據采集總時間為400 s，試驗結果(選取1 Hz～40 Hz)如圖13 所示，其中縱坐標表示歸一化(1×10-6為參考值)的機械設備振動加速度響應幅值。

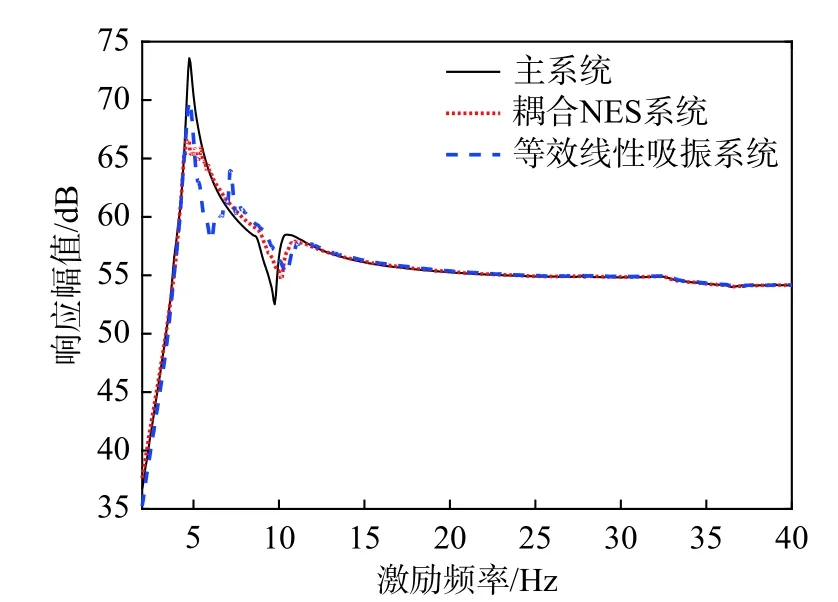
圖13 掃頻試驗結果Fig. 13 The sweep-frequency test results

從圖13 可知，不加吸振器時主系統一階與二階固有頻率分別在5.00 Hz 和10.44 Hz 附近，響應幅值分別為73.60 dB 和58.48 dB；當耦合等效線性吸振器(柔性鉸鏈不施加預壓力)時，在4.75 Hz～6.82 Hz 范圍內，吸振效果較為明顯，一階共振峰降低了3.74 dB，同時系統在7.63 Hz 和7.19 Hz 附近產生了2 根強度顯著新的共振峰；當耦合NES時，一方面在5.0 Hz 附近一階共振峰降低了8.17 dB，另一方面在4.43 Hz～5.82 Hz 范圍內，系統響應曲線較為平緩，平均線譜強度降低了約3.74 dB，原一階共振峰消失且未產生新的共振峰。因此，NES和等效線性吸振器相比，展現了良好的寬頻吸振效果。

另外，定頻試驗結果如圖14 所示。從圖中可知，若外界激勵頻率等于一階固有頻率5.00 Hz時，未耦合NES 時機械設備呈現周期運動，加速度響應幅值為0.488 m/s2；當耦合NES 后，激勵頻率為5.00 Hz 和5.31 Hz 時，機械設備加速度響應平均幅值約為0.195 m/s2和0.189 m/s2，與未耦合NES 時相比，響應幅值降低了約60.04%和61.27%。而且兩個振子響應形式出現了顯著變化，均呈現強調制響應狀態。

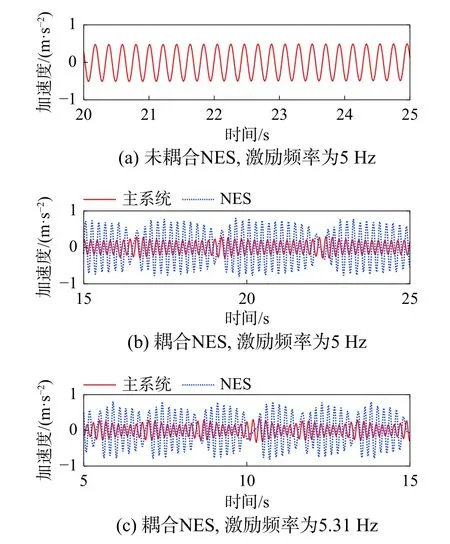
圖14 系統振動響應時間歷程圖Fig. 14 Time histories of the system vibration response

6 結論

結合潛艇機械設備垂向振動控制需求，本文通過理論分析、數值仿真以及試驗研究的方法，開展了簡諧激勵條件下立方剛度NES 振動抑制效果研究，主要得到以下結論：

(1) IHB 法、弧長延拓法以及Floquet 理論三者結合起來能夠有效解析NES 系統周期解與分岔點信息，并與Runge-Kutta 數值計算結果吻合良好。

(2) NES 振動抑制效果與阻尼、質量比以及剛度均密切相關，并且是非線性變化的，只有在弱阻尼條件下，而且質量和剛度參數取得適中時，才可能出現理想的振動抑制效果。

(3) NES 存在局部最優參數，其振動抑制效果隨剛度更加敏感，在參數優化區域內，系統呈現強調制響應狀態；對于參數優化后的非線性能量阱，其具有良好的寬頻吸振效果及魯棒性。

(4) 試驗結果表明，柔性鉸鏈型NES 結構垂向力-位移曲線呈現立方剛度特性，且使主系統5.0 Hz處一階共振峰降低了8.17 dB，4.43 Hz～5.82 Hz 范圍平均線譜強度降低3.74 dB，和等效線性吸振器相比，具有較佳的寬頻吸振效果。同時，NES 系統在吸振頻帶內的運動狀態呈現強調制響應。