基于人工智能技術(shù)的輸氣管道系統(tǒng)可靠性量化方法

朱汪友 侯 磊

1.中國石油大學（北京） 2.國家石油天然氣管網(wǎng)集團有限公司北方管道有限責任公司

0 引言

油氣管道是關(guān)乎國民經(jīng)濟持續(xù)、穩(wěn)定發(fā)展和人民生活的能源命脈。2017年印發(fā)的《關(guān)于深化石油天然氣體制改革的若干意見》，明確了油氣體制改革是包括上中下游全產(chǎn)業(yè)鏈的改革，其基本思路是“管住中間，放開兩頭”。“中間”即管網(wǎng)輸送環(huán)節(jié)。油氣體制改革的目的是推進管輸環(huán)節(jié)公平開放，提升集約輸送和公平服務能力。在此背景下，國家石油天然氣管網(wǎng)集團有限公司（以下簡稱國家管網(wǎng)公司）于2019年12月9日正式組建成立，負責全國油氣干線管網(wǎng)的建設和調(diào)度運行。國家管網(wǎng)公司的成立有助于形成上游油氣資源多主體多渠道供應、中間統(tǒng)一管網(wǎng)高效集輸、下游銷售市場充分競爭的“X+1+X”油氣市場體系，提升了油氣資源全局優(yōu)化能力及利用效率。

當前，國家管網(wǎng)公司所轄天然氣管道總里程約5×104km，“X+1+X” 油氣市場體系和橫跨東西、縱貫南北的“全國一張網(wǎng)”的天然氣干線管網(wǎng)運營機制逐步形成。但是，較之于其他世界主要經(jīng)濟體，中國天然氣管網(wǎng)的系統(tǒng)冗余度小[1-3]，拓撲結(jié)構(gòu)相對復雜、用氣不均衡性突出，導致天然氣保供狀態(tài)下部分管道所承擔的輸送任務極重，一旦出現(xiàn)局部失效，管網(wǎng)系統(tǒng)應對措施有限，天然氣管網(wǎng)系統(tǒng)的供氣安全與生產(chǎn)安全難以保障。供氣安全即管網(wǎng)系統(tǒng)有足夠的資源和輸送能力，保證在規(guī)定時間內(nèi)能夠滿足用戶日常及用氣高峰需求；生產(chǎn)安全即管網(wǎng)系統(tǒng)中各組成部分的安全性處于可控、受控狀態(tài)，并確保在事故狀態(tài)下可以避免連鎖反應而不至于由此引發(fā)整個管網(wǎng)系統(tǒng)失控和大面積停輸[4]。

黃維和等[4-5]于2013年首次將可靠性理論、方法、技術(shù)體系創(chuàng)新性地與油氣管道行業(yè)運行特點及業(yè)務需求結(jié)合起來，以應對大型復雜管網(wǎng)的生產(chǎn)安全及供氣安全的挑戰(zhàn)——通過建立包含可靠性指標、可靠性計算模型、可靠性增強方法的技術(shù)體系從而實現(xiàn)可靠性閉環(huán)。該體系使用可靠性指標以明確管網(wǎng)系統(tǒng)可靠性的內(nèi)涵和實質(zhì)，建立可靠性計算模型以量化管網(wǎng)系統(tǒng)的可靠性、分析系統(tǒng)的薄弱環(huán)節(jié)，采用可靠性增強方法以使系統(tǒng)可靠性數(shù)值達到目標要求。可靠性技術(shù)及管理有利于決策者從全局高度優(yōu)化管網(wǎng)安全管理，以實現(xiàn)對全國管網(wǎng)系統(tǒng)可靠性信息的全面掌控與統(tǒng)籌管理。艾慕陽[1-2]基于黃維和等的研究，進一步細化了可靠性指標，提出了管網(wǎng)系統(tǒng)單元層級可靠性的相關(guān)函數(shù)。

艾慕陽[1-2]、黃維和等[4-5]及其他相關(guān)研究人員[6-8]將系統(tǒng)可靠性與管道行業(yè)的輸送特點結(jié)合起來，明確了由于輸送負荷不同，不僅有可能導致元件的工作條件變化，而且還有可能影響系統(tǒng)可靠性邏輯關(guān)系——可靠性邏輯關(guān)系因輸送負荷不同有可能會引入非線性，從而導致基于傳統(tǒng)的可靠性串聯(lián)、可靠性并聯(lián)及K/N決策系統(tǒng)等簡單可靠性邏輯在管道行業(yè)系統(tǒng)層級并不適用。因此，當前油氣管道業(yè)界對于輸送負荷的不確定性以及管網(wǎng)系統(tǒng)的可靠性開展研究已迫在眉睫。

天然氣管網(wǎng)系統(tǒng)作為點多、線長、面廣的開放式大系統(tǒng)，具有以下特點：①就管網(wǎng)物理本體而言，其途經(jīng)復雜地質(zhì)地貌地區(qū)，生態(tài)敏感點眾多、沿線人文社會環(huán)境復雜；②從供需角度來看，其資源多元化、市場分布廣；③從運行管理角度來看，其管輸不平衡性突出，同時面臨著多目標運行條件下的效率提升壓力；④更為重要的是，隨著上游資源多主體多渠道供應“X”的形成和對下游銷售市場充分競爭“X”的定位、認知，運行機制、運行平臺的逐步清晰和深化[3]，管網(wǎng)的運行及輸送負荷將面臨更大的不確定性。管網(wǎng)系統(tǒng)的可靠性是指其在給定的工作條件下、在給定的時間段內(nèi)完成給定運輸任務的概率，因而短周期輸送負荷的變化、運行條件的不確定性都必然會帶來系統(tǒng)可靠性的變化。筆者認為，可以基于多源異構(gòu)海量數(shù)據(jù)（大數(shù)據(jù)）的采集、預處理、分析，創(chuàng)新性地應用人工智能技術(shù)開展模擬及預測分析，以降低管網(wǎng)系統(tǒng)的不確定性，以期為解決“全國一張網(wǎng)”大背景下的天然氣管網(wǎng)系統(tǒng)可靠性計算及分析難題提供一種新方法。

覃偉中[9-10]等基于九江石化智能化建設成果，通過將新一代信息技術(shù)與工業(yè)業(yè)務結(jié)合，為解決不確定性問題探索出了一條成功之路。唐善華等[11]基于多源多維度復雜的工業(yè)數(shù)據(jù)，采用數(shù)據(jù)處理技術(shù)和人工智能領(lǐng)域的深度學習算法用于解決管網(wǎng)短周期消費量預測、實時平衡分析及監(jiān)控、運行方案推薦等生產(chǎn)需求。通過工業(yè)實踐充分證明了人工智能技術(shù)由于其自身特點可以有效應對大型復雜系統(tǒng)的不確定性問題。

為了保障“全國一張網(wǎng)”的天然氣干線管網(wǎng)運營機制以及上游油氣資源多主體多渠道供應、中間“一張網(wǎng)”高效集輸、下游市場化良性競爭油氣市場體系（“X+1+X”體系）的安全穩(wěn)定運行，筆者首次提出了基于人工智能技術(shù)的天然氣管道系統(tǒng)可靠性量化方法，通過采用長短期記憶神經(jīng)網(wǎng)絡（LSTM）方法進行短周期用氣量預測；短周期用氣量確定后，管道的輸送負荷也隨之確定，在給定時間內(nèi)，管道系統(tǒng)的運行條件也隨之相對確定。因此系統(tǒng)生產(chǎn)運行的不確定性大大降低，從而保障了可靠性計算結(jié)果的正確性及適用性。本文依次介紹了天然氣管道系統(tǒng)可靠性模型、天然氣管道系統(tǒng)可靠性計算方法、實際應用案例及結(jié)論。

1 天然氣管道系統(tǒng)可靠性模型

管道系統(tǒng)可靠性量化方法是管網(wǎng)系統(tǒng)可靠性計算的基礎，也是量化全國管網(wǎng)的可靠性、分析其系統(tǒng)薄弱環(huán)節(jié)、采取管理及技術(shù)措施進行可靠性增強的前提。管道系統(tǒng)可靠性模型從數(shù)學上展示了管道系統(tǒng)可靠性與其輸送壓力及用戶需求量的相關(guān)性。因此，筆者采用了LSTM方法對短周期用氣量進行預測，通過采用貝葉斯理論、“N–1原則”及預測的用氣量數(shù)值，提出了量化管道系統(tǒng)可靠性的方法，并且選擇實際天然氣管道對所提出的方法進行了驗證。

20世紀30年代末，系統(tǒng)可靠性研究正式被提出，航空航天、電力系統(tǒng)、電子工業(yè)等領(lǐng)域較早引入可靠性技術(shù)，形成了多種可靠性理論和計算方法，如故障樹結(jié)構(gòu)的事故分析技術(shù)、事件樹結(jié)構(gòu)的可靠性分析技術(shù)、Bayesian方法、系統(tǒng)可靠性快速評估法、可靠性計算的遞推法、系統(tǒng)可靠性蒙特卡羅（Monte Carlo）仿真算法等。可靠性計算是可靠性技術(shù)的核心，目前常用的兩種基本方法分別是解析法和Monte Carlo模擬法。

解析法[12-14]主要通過對產(chǎn)品性能、工況及故障等數(shù)據(jù)進行統(tǒng)計分析，利用系統(tǒng)結(jié)構(gòu)、元件功能及兩者之間的邏輯關(guān)系（如串并聯(lián)系統(tǒng)、K/N系統(tǒng)等），建立可靠性框圖及概率模型，通過遞推和迭代等過程對模型精確求解，從而計算可靠性指標。該方法的優(yōu)點在于采用精確數(shù)學模型、計算準確度較高，但對于復雜系統(tǒng)，解析法計算維度大，并且為了獲得解析模型通常都需要對系統(tǒng)實際條件作較多的簡化。因此其應用受到較大的限制。

Monte Carlo模擬法[15]是一種以概率統(tǒng)計理論和方法為基礎的數(shù)值計算方法，與故障樹分析技術(shù)相結(jié)合，可以對系統(tǒng)進行有效的可靠性分析計算。該方法采用數(shù)值計算方法模擬實際過程，并從大量模擬試驗結(jié)果中統(tǒng)計系統(tǒng)可靠性指標。模擬法不需要對實際問題作過多的簡化和假設，但計算精度相對較低。

傳統(tǒng)可靠性理論中，系統(tǒng)只有正常工作和完全失效兩種狀態(tài)。系統(tǒng)可靠性函數(shù)可退化為僅與時間相關(guān)的狀態(tài)函數(shù)，計算過程得以大大簡化，通常稱之為基于極限狀態(tài)的可靠性函數(shù)計算方法。無論是解析法還是Monte Carlo模擬法，基本上針對的都是系統(tǒng)額定工況。

然而，如前所述，對于在較寬工況范圍內(nèi)可以長期穩(wěn)定運行的輸氣管網(wǎng)系統(tǒng)而言，僅表述單一工況是不夠的。這樣既沒有顧及管網(wǎng)運行工況差異，也不能表達管網(wǎng)的能力變化。特別是冬季天然氣保供期內(nèi)，部分管道管輸負荷極大，導致管網(wǎng)整體輸送不平衡性突出。依據(jù)定性分析結(jié)果可知，在壓力、輸量等工藝參數(shù)動態(tài)變化的情況下，管網(wǎng)系統(tǒng)各組成部分可靠性數(shù)值有變化。因此管網(wǎng)系統(tǒng)可靠性技術(shù)及管理需將短周期負荷變化納入可靠性計算分析的范疇中，統(tǒng)籌考慮管網(wǎng)輸量與安全性。本文重點研究單條天然氣管道系統(tǒng)的可靠性，進而為天然氣管網(wǎng)系統(tǒng)的可靠性計算分析奠定技術(shù)基礎。

單條管道系統(tǒng)的可靠性模型如圖1、2所示，為了不喪失代表性和一般性，可以假設用戶在系統(tǒng)末端，圖1、2中的STi、Pi分別代表第i個站、第i個管段，站及管段在文中統(tǒng)稱為“子系統(tǒng)”。

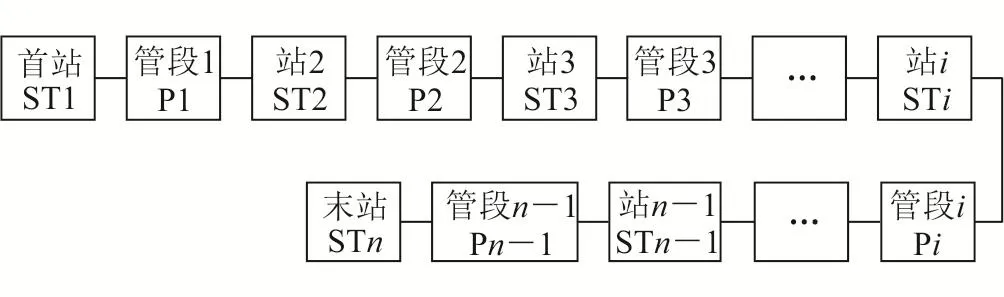
圖1 天然氣管道系統(tǒng)拓撲結(jié)構(gòu)示意圖

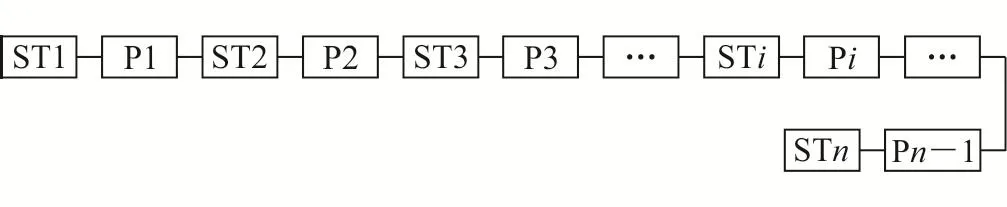
圖2 單條天然氣管道系統(tǒng)可靠性框圖

可靠性計算的基本原則如下：

1）“N–1原則”，當子系統(tǒng)失效個數(shù)大于1時，系統(tǒng)應被視為失效狀態(tài)，即N–1原則。采用N–1原則，可以避免大量的計算成本和額外數(shù)據(jù)需求。

2）若最后一個管段Pn－1或最后一個站STn失效，則認為系統(tǒng)失效。

此外，由于系統(tǒng)的可靠性與上述運輸功能有關(guān)，因此應滿足以下條件：①如p≥psev，則系統(tǒng)供氣正常；②如p＜pmin，系統(tǒng)的供氣不符合用戶需求；③如pmin≤p＜psev，系統(tǒng)進行部分供氣。

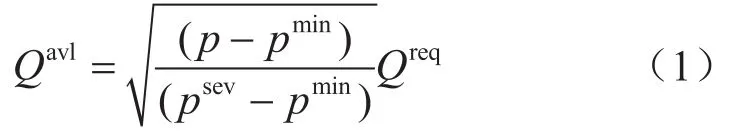
式中Qavl表示實際輸送能力，Nm3/s；p表示當前（給定）運行壓力，MPa；pmin表示城市門站所需的最低供氣壓力；psev表示正常輸送壓力，MPa；Qreq表示用戶要求的輸量，Nm3/s。

2 天然氣管道系統(tǒng)可靠性計算方法

2.1 基于大數(shù)據(jù)及人工智能技術(shù)的天然氣輸量預測模型

天然氣用戶用氣量預測是典型的時間序列問題，對其進行預測的傳統(tǒng)模型包括兩類：①以自回歸積分滑動平均模型為代表的傳統(tǒng)時間序列；②機器學習模型，如使用BP神經(jīng)網(wǎng)絡、支持向量機（SVM）等進行預測。傳統(tǒng)機器學習算法模型復雜度低，難以加入時間序列維度信息，預測準確度相對較低。因此，近年來多采用遞歸神經(jīng)網(wǎng)絡（RNN）類模型來對天然氣管網(wǎng)的日（小時）輸量進行預測。該方法隱藏層神經(jīng)元之間帶權(quán)重數(shù)值，隨著序列推進，前隱藏層將會影響到后隱藏層，因而可以對時間序列信息進行表達。然而標準RNN模型隨著序列的逐步推進，會存在梯度消失現(xiàn)象，即不同隱藏層雖然存在過去時刻對當前時刻的影響，但隨著時間跨度變大上述影響會被削弱。因此業(yè)界提出了基于RNN的改進模型，長短期記憶神經(jīng)網(wǎng)絡（LSTM），以確定過去信息對當前信息的影響。

對應迭代公式如下：

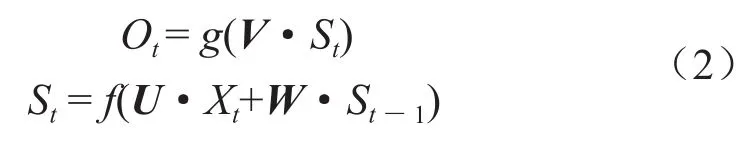
式中向量O表示輸出層的值；V表示隱藏層到輸出層的權(quán)重矩陣；向量S表示隱藏層的值；U表示輸入層到隱藏層的權(quán)重矩陣；向量X表示輸入層的值；W表示隱藏層上一次的值作為本次輸入的權(quán)重矩陣；下標t表示時間。

2.1.1 數(shù)據(jù)采集

天然氣輸量預測的所用數(shù)據(jù)來源于管道基礎數(shù)據(jù)、時間序列數(shù)據(jù)、運行報表數(shù)據(jù)、數(shù)據(jù)采集與監(jiān)視控制系統(tǒng)（SCADA）實時數(shù)據(jù)、仿真模擬計算數(shù)據(jù)、管道生產(chǎn)系統(tǒng)（PPS）的日運行數(shù)據(jù)、氣象數(shù)據(jù)、非結(jié)構(gòu)化數(shù)據(jù)（表1），特征數(shù)據(jù)來源于節(jié)假日信息及歷史天氣數(shù)據(jù)和預報數(shù)據(jù)。

表1 用于天然氣輸量預測的基礎數(shù)據(jù)分類表

表1中的SCADA實時數(shù)據(jù)通過中間數(shù)據(jù)庫獲取，氣象數(shù)據(jù)獲取自氣象大數(shù)據(jù)服務商的API，氣源及輸量數(shù)據(jù)自PPS系統(tǒng)獲取。上述數(shù)據(jù)中既有實時動態(tài)數(shù)據(jù)，也有靜態(tài)數(shù)據(jù)，既包括結(jié)構(gòu)化數(shù)據(jù)，也包括非結(jié)構(gòu)化數(shù)據(jù)，屬于典型的多源異構(gòu)海量大數(shù)據(jù)范疇。

2.1.2 實驗方法

LSTM數(shù)據(jù)輸入的數(shù)據(jù)格式為NF矩陣加上時間軸后的數(shù)據(jù)立方體，即時間軸上的切片，第一、第二、第三維度分別為樣本數(shù)、時間及特征數(shù)。

上述數(shù)據(jù)集是一個多元時間序列數(shù)據(jù)集，描述城市指定時間內(nèi)的用氣量。本文用氣量數(shù)據(jù)時間跨度為2021年1月至2021年7月。歷史天氣數(shù)據(jù)從天氣運營商提供的API服務中獲取，通過自定義及開發(fā)程序?qū)⒏鲾?shù)據(jù)通過日期聚合在一起，形成的基本數(shù)據(jù)集包括時間（日期）、日用氣量（小時用氣量）、日最高溫度、日最低溫度、是否節(jié)假日、風力、風向、天氣狀態(tài)、空氣質(zhì)量、濕度等。采用訓練參數(shù)如下：特征維數(shù)為9，隱藏層神經(jīng)元個數(shù)為256， LSTM 堆疊的層數(shù)為10。

模型訓練后，日用氣量最終損失曲線的累積損失誤差達到了收斂條件。選取某天然氣管道從2021年1月1日至2021年7月11日共計192天真實日用氣量數(shù)據(jù)中的前186天的日輸量作為訓練數(shù)據(jù)，最后6天作為測試數(shù)據(jù)，采用LSTM方法進行預測比較，實驗結(jié)果如圖3、4所示。從圖3、4中可以看出，訓練數(shù)據(jù)與預測結(jié)果基本無誤差，真實數(shù)據(jù)（測試數(shù)據(jù)）與使用人工智能算法計算結(jié)果的平均誤差約為4%，最小誤差小于1%，滿足了工業(yè)化應用的要求。

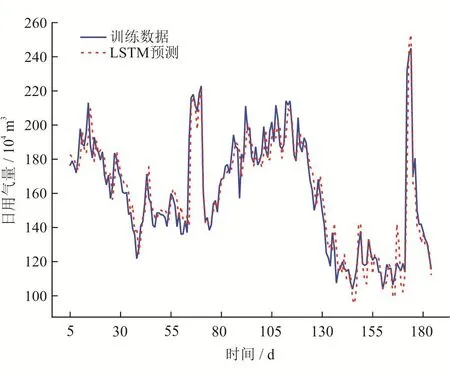
圖3 日用氣量訓練數(shù)據(jù)驗證圖

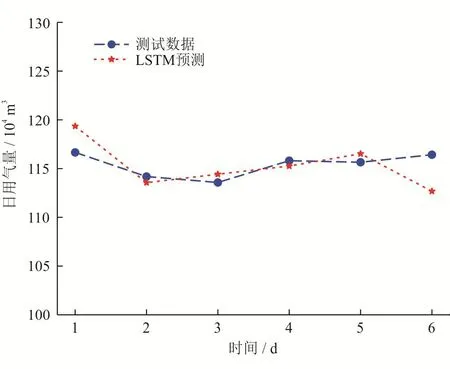
圖4 日用氣量預測值與真實值對比圖

日用氣量數(shù)據(jù)的數(shù)據(jù)樣本因工業(yè)數(shù)據(jù)采集系統(tǒng)存儲容量及策略的原因相對較少，因而選取了小時級的用氣量數(shù)據(jù)對本文所提出的方法進行再次驗證。通過選取某天然氣管道從2021年1月1日至2021年7月11日總計4 608 h（192天）用氣量數(shù)據(jù)中的前4 584個樣本作為訓練數(shù)據(jù)，后24個數(shù)據(jù)作為測試數(shù)據(jù)，采用LSTM方法進行預測比較，實驗結(jié)果如圖5所示。從圖5可以看出，真實數(shù)據(jù)（測試數(shù)據(jù)）與使用人工智能算法計算結(jié)果的平均誤差約為2%，最小誤差小于0.1%，數(shù)據(jù)樣本的大幅度增加有效提升了應用效果。

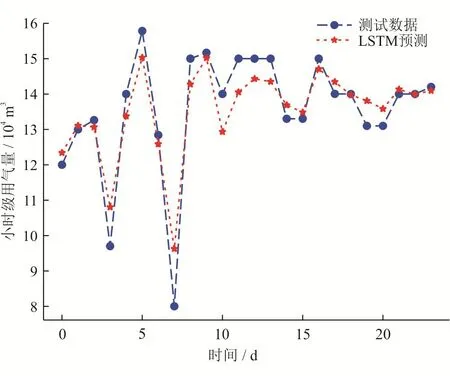
圖5 小時級用氣量預測值與真實值對比圖

LSTM模型的初始參數(shù)如下：特征維數(shù)為9，隱藏層神經(jīng)元個數(shù)為256， LSTM 堆疊的層數(shù)為10，一次性輸入的訓練序列數(shù)為20（向量數(shù)據(jù)），初始誤差為6.9%。LSTM的輸入為4 584個樣本，輸入特征向量為溫度、風力、天氣狀態(tài)、PM2.5濃度、節(jié)假日、用氣量等數(shù)據(jù)，輸出為24個預測數(shù)據(jù)。

2.2 天然氣管道系統(tǒng)可靠性計算

2.2.1 貝葉斯理論及其在可靠性計算中的應用

貝葉斯技術(shù)因其兼容隨機變量的不確定性和相關(guān)性，可以彌補傳統(tǒng)可靠性評估方法的不足[16-19]。由于貝葉斯網(wǎng)絡結(jié)構(gòu)的特點和雙向推理的優(yōu)勢，在進行系統(tǒng)可靠性研究中，可以直接計算一個元件或多個元件故障對系統(tǒng)故障的影響，以及系統(tǒng)故障條件下元件的故障概率，避免了最小割集及重要度計算。

貝葉斯網(wǎng)絡是一個有向無環(huán)圖（DAG），它由代表變量的節(jié)點及連接這些節(jié)點的有向邊構(gòu)成。其中節(jié)點代表論域中的變量，有向弧代表變量間的關(guān)系（影響概率），通過圖形表達不確定性知識，通過條件概率分布（CPD）的注釋，可以在模型中表達局部條件的依賴性。按照貝葉斯公式給出的條件概率定義：

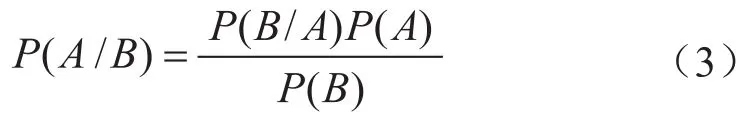
式中P(A/B)表示后驗概率；P(B/A)表示似然率；P(A)表示后驗概率；P(B)表示先驗概率。

假設A是一個變量，存在著n個狀態(tài)a1,a2, …ai, …,an，則由全概率公式可以得出：

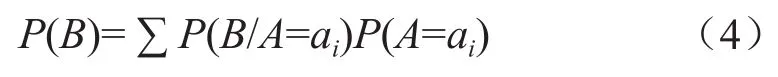
從而根據(jù)貝葉斯公式算出后驗概率P(A/B)。貝葉斯網(wǎng)絡不但可以實現(xiàn)正向推理，由先驗概率推導出后驗概率，即由原因?qū)С鼋Y(jié)果，還可以利用公式由后驗概率推導出先驗概率，即由結(jié)果導出原因。

貝葉斯方法多用于評估油氣管道腐蝕可靠性、結(jié)構(gòu)可靠性和管道剩余壽命分析。CHEN[20]、張杰等[21]基于貝葉斯理論對腐蝕管道可靠性評價進行了研究，提出小樣本條件下管道腐蝕、結(jié)構(gòu)可靠性的貝葉斯推斷法。

2.2.2 元件（組件）可靠性計算

管網(wǎng)系統(tǒng)可靠性指標是開展天然氣管網(wǎng)系統(tǒng)可靠性評價的前提，其所考量的可靠性指標又可以進一步細分為管網(wǎng)系統(tǒng)、管道系統(tǒng)、站場及單元層級，單元層級則包括管段、壓縮機組、閥門、工藝管道等各級系統(tǒng)的主要組成要素。

管網(wǎng)系統(tǒng)單元眾多，應根據(jù)不同特點選擇不同的可靠性計算方法來計算其可靠度。如針對含缺陷管道和埋地懸空管道的斷裂失效模式，結(jié)合受力特征，采用蒙特卡洛模擬方法計算其可靠度；針對管段第三方破壞，采用故障樹分析方法，從管道遭受第三方破壞活動沖擊概率和沖擊力作用下管道失效概率兩個方面，建立了可靠度計算模型。需要說明的是，目前各單元可靠性模型的使用條件均是在指定工況條件下，即壓力、流量、溫度均為定值[22-25]，但對于在較寬工況范圍內(nèi)可以長期穩(wěn)定運行的大型油氣管網(wǎng)系統(tǒng)而言，僅表述單一工況是不夠的，未來尚需逐步研究將可靠性函數(shù)的“規(guī)定條件”和“規(guī)定功能”由單一狀態(tài)拓展為選定區(qū)間，即壓力、流量、溫度在某區(qū)間內(nèi)變化。

采用基于典型結(jié)構(gòu)的“分布式階梯式”站場可靠度計算模型，將站場模型（壓氣站、聯(lián)絡站、分輸站3種類型）分為站場、典型結(jié)構(gòu)、基本回路及設備單元4個層級進行建模，建模時采用模塊化建模的方式。站場可靠度計算流程如圖6所示。基于SCADA或仿真系統(tǒng)的輸送狀態(tài)，可得出各模塊的可靠性邏輯計算模型。設備單元可靠度需結(jié)合設備單元的運行參數(shù)（從可靠性數(shù)據(jù)庫中獲取）進行計算。

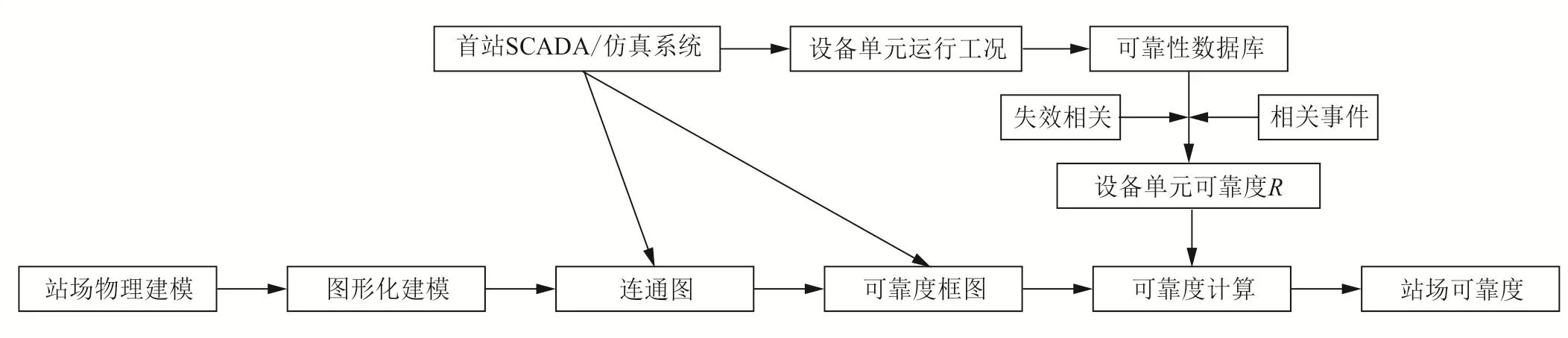
圖6 站場可靠度計算流程圖

可靠性計算所需數(shù)據(jù)及數(shù)據(jù)傳遞關(guān)系如圖7所示。首先，可靠性數(shù)據(jù)庫從其他信息系統(tǒng)，如資產(chǎn)完整性系統(tǒng)（PIS）或管理信息系統(tǒng)（ERP）獲取可靠性相關(guān)數(shù)據(jù)信息，缺失數(shù)據(jù)通過單元可靠性的研究成果補充。同時從SCADA中獲取每個設備的歷史工作區(qū)間。其次，計算引擎從仿真/SCADA系統(tǒng)獲取單元當前運行工況（p、Q、T）并從可靠性數(shù)據(jù)庫中調(diào)取單元在此運行狀態(tài)下的可靠度數(shù)值。

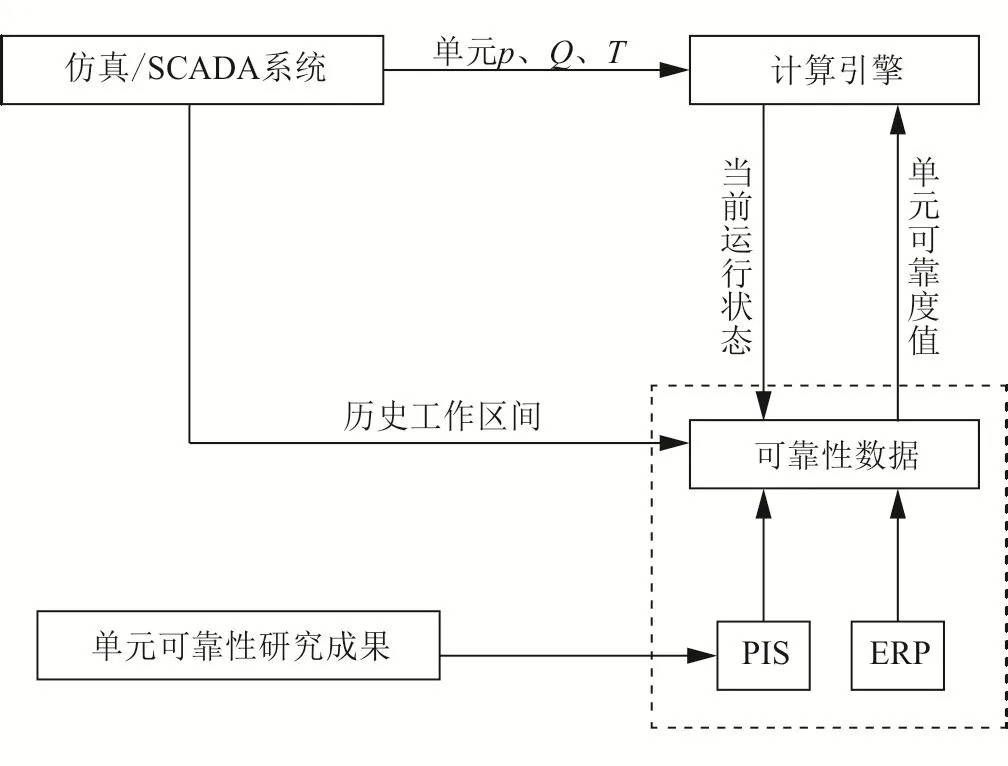
圖7 各系統(tǒng)間數(shù)據(jù)傳遞關(guān)系圖

2.2.3 管道系統(tǒng)可靠性計算

假設第i個站的可靠性用表示RSTi，第i個管段的可靠性用RPi表示，單個管道系統(tǒng)的可靠性用RS表示。根據(jù)貝葉斯理論，系統(tǒng)的可靠性應由式（5）計算：

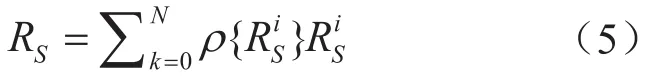
基于貝葉斯理論的特性，式（5）為系統(tǒng)可靠性的所有可能方案的解空間。

考慮N–1原則，則只需計算如下2個事件的發(fā)生可能性及其對應的可靠性。

2.2.3.1 事件1，所有子系統(tǒng)均為正常狀態(tài)

該條件下事件發(fā)生的可能性及對應的可靠性可通過下式計算：

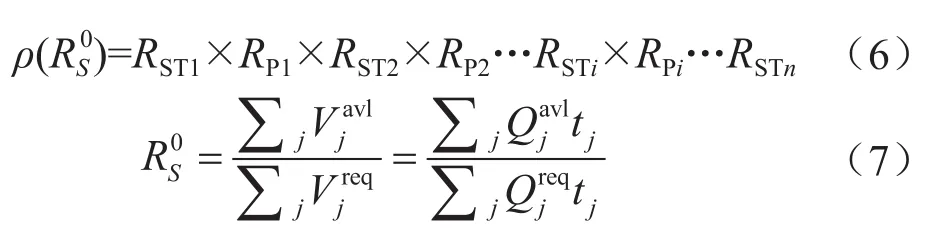
2.2.3.2 事件2，只有一個子系統(tǒng)處于失效狀態(tài)

該事件又可細分為以下3類：

1）最后一個站或最后一個管段發(fā)生故障，則系統(tǒng)無法完成輸氣任務，因此系統(tǒng)的可靠度為0。

2）僅第i個站失效：在T時間段內(nèi)，當?shù)趇(1＜i＜2n–2)個站失效時，假設失效時間為Ti(0≤Ti≤T)。由于第i個站失效，系統(tǒng)壓力p發(fā)生變化，其他子系統(tǒng)的可靠度也變化為

若系統(tǒng)壓力p滿足pmin≤p＜psev，由于管道系統(tǒng)的自身儲氣能力，系統(tǒng)能夠持續(xù)輸送氣體的時間為Ti1(0≤Ti1≤Ti)，則系統(tǒng)可靠度為：

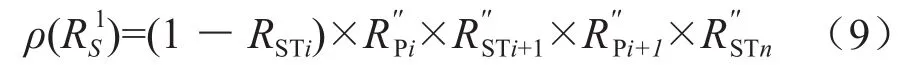
在時間段Ti2內(nèi)，Ti2(0≤Ti2≤Ti)，Ti1+Ti2=Ti。元件i繼續(xù)失效，供氣不足或壓力過小不能輸送，可靠度為0。

3）僅第i個管段失效：如果系統(tǒng)壓力p滿足p≤pmin＜psev，由于管道系統(tǒng)的儲氣能力，系統(tǒng)可以持續(xù)輸送氣體的時間為Ti1(0≤Ti1≤Ti)，則系統(tǒng)可靠度：

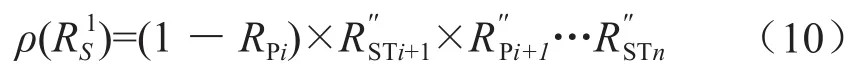
在時間段Ti2內(nèi)，Ti2(0≤Ti2≤Ti)，Ti1+Ti2=Ti，元件i持續(xù)失效，供氣不足，系統(tǒng)可靠度為0。

3 實際應用案例

為驗證本文所提出方法的可靠性，選取了一條真實的天然氣管道進行實用性分析，該管道系統(tǒng)由12個站點、41個閥室和5個管段組成（圖8）。

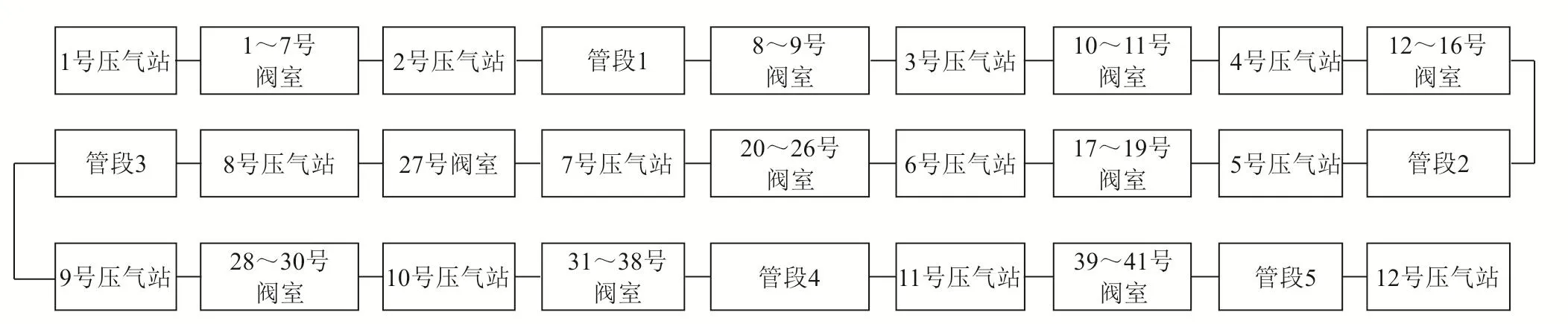
圖8 實際應用天然氣管道示意圖

3.1 元件可靠性計算結(jié)果

閥門、壓縮機、過濾器的可靠性分別為0.996 94、0.955 30、0.906 00。其中閥室的可靠性可通過使用串并聯(lián)系統(tǒng)可靠性模型計算獲得。

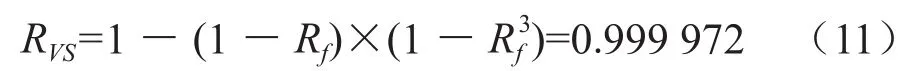
式中RVS表示閥室的可靠度；Rf表示組成閥室的閥門的可靠度。

站場可靠度計算采用基于典型結(jié)構(gòu)的“分布式階梯式”站場可靠度計算模型，將站場模型分為站場、典型結(jié)構(gòu)、基本回路及設備單元4個層級，壓氣站、聯(lián)絡站、分輸站3種類型進行建模。以壓氣站為例進行說明，如圖9所示。

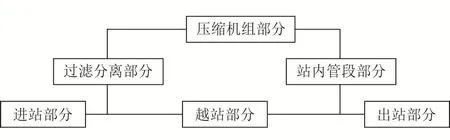
圖9 壓氣站場可靠性框圖

計算步驟：①基于進、出站部分的可靠性邏輯結(jié)構(gòu)，采用串并聯(lián)模型進行計算；②過濾分離部分采用并聯(lián)模型進行計算；③壓縮機組部分采用k/N系統(tǒng)計算；④站內(nèi)工藝管道基于故障率進行計算。

壓氣站場可靠度模型由進站部分、過濾分離部分、壓縮機組部分等組成的串聯(lián)模型。根據(jù)串聯(lián)系統(tǒng)可靠度計算模型可以計算其可靠度。同理可以進行分輸站、聯(lián)絡站等站場可靠度計算。

k/N系統(tǒng)由n個元件組成。當n個元件中至少有k個元件正常工作時，系統(tǒng)才算正常工作，即失效的部件數(shù)小于等于n－k時，系統(tǒng)正常工作。當系統(tǒng)中失效的元件數(shù)大于n－k時系統(tǒng)失效。其可靠度計算公式為：

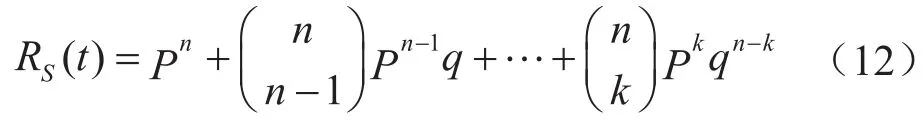
式中RS(t)為壓縮機組可靠度；P為每臺壓縮機正常工作概率；q為每臺壓縮機的失效概率；q+P=1。

3.2 子系統(tǒng)可靠性計算結(jié)果

根據(jù)輸送方案和設備單元可靠度信息如表2所示，基于站場典型結(jié)構(gòu)，在不同運輸工況下，基于智能化仿真技術(shù)，計算天然氣干線管道各站點的可靠度結(jié)果（表3）。

表2 站場設備可靠性信息統(tǒng)計表

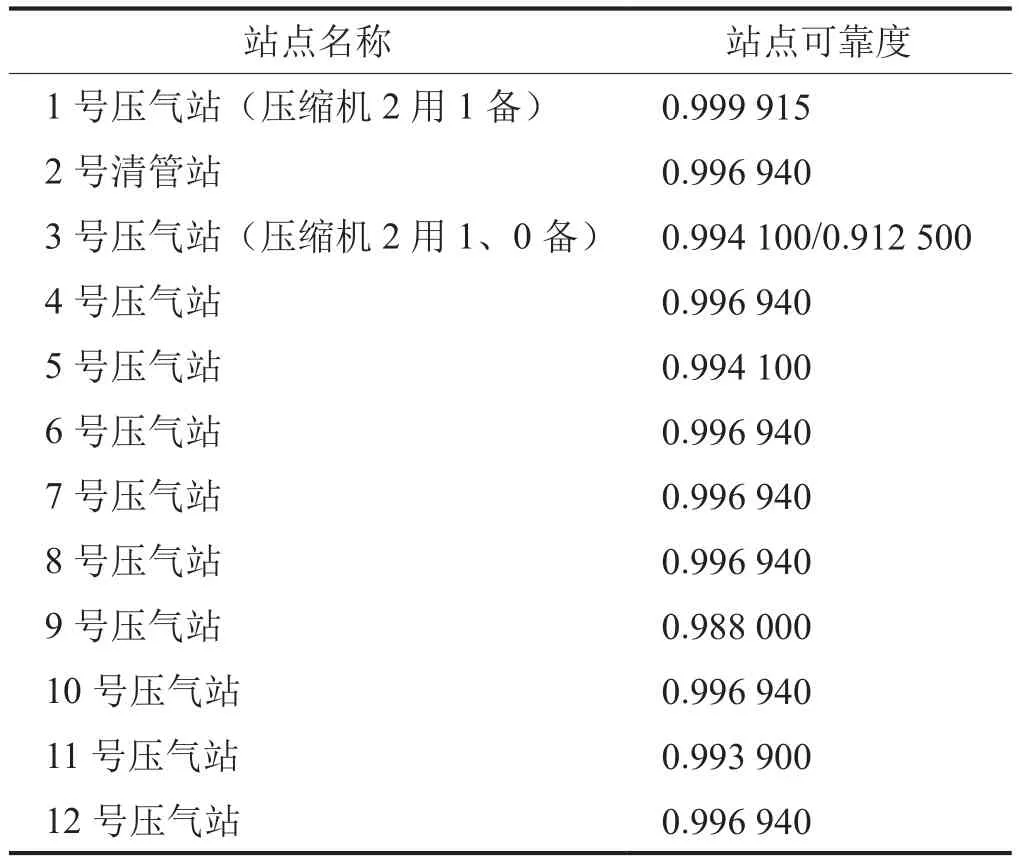
表3 各站點可靠度計算結(jié)果表

管段的可靠度可以綜合考慮各外部因素對其安全可靠性的影響（表4），即：

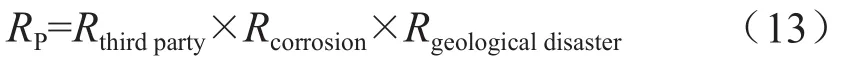
式中RP表示管段可靠度；Rthirdparty表示管段第三方破壞可靠度；Rcorrosion表示腐蝕可靠度；Rgeologicaldisaster表示地質(zhì)災害可靠度。

3.3 天然氣管道系統(tǒng)可靠性計算結(jié)果

由所選天然氣管道系統(tǒng)在不同運行條件下的系統(tǒng)可靠性（表5）可以看出，不同運行條件下，系統(tǒng)的可靠度數(shù)值也隨之改變。當冬季天然氣保供時，由于用氣量預測模型計算出系統(tǒng)輸量，系統(tǒng)運行狀態(tài)也隨之改變，可靠度數(shù)值也對應改變。

表5 不同運行條件下的系統(tǒng)可靠度統(tǒng)計表

4 結(jié)論

1）根據(jù)天然氣“全國一張網(wǎng)”互聯(lián)互通“十四五”建設規(guī)劃，預計到2025年，中國將形成合計長度達16.3×104km的天然氣大管網(wǎng)。同時，隨著市場化運行機制的不斷深化及天然氣管網(wǎng)數(shù)字化、網(wǎng)絡化、智能化的持續(xù)發(fā)展，天然氣管網(wǎng)這一開放式大型復雜系統(tǒng)將有可能面臨更多的技術(shù)挑戰(zhàn)，包括管網(wǎng)基礎設施的安全可靠性、復雜多變的外部運行環(huán)境、特殊事件的沖擊及各層面的不確定性。客觀上需要借助人工智能技術(shù)、大數(shù)據(jù)分析及可靠性技術(shù)來量化管網(wǎng)系統(tǒng)可靠性。通過將人工智能技術(shù)應用于天然氣管道系統(tǒng)可靠性計算，可以為量化全國天然氣管網(wǎng)的可靠性探索出一條可行的技術(shù)路徑，從而為分析系統(tǒng)薄弱環(huán)節(jié)、采取管理及技術(shù)措施以增強可靠性的奠定基礎。

2）國家管網(wǎng)公司積累了海量的實時數(shù)據(jù)、歷史數(shù)據(jù)、性能監(jiān)測數(shù)據(jù)、仿真結(jié)果數(shù)據(jù)及管理數(shù)據(jù)，管網(wǎng)系統(tǒng)的生產(chǎn)運行數(shù)據(jù)具有較強時序性、數(shù)據(jù)關(guān)聯(lián)性強，可以采用LSTM等人工智能技術(shù)基于管網(wǎng)系統(tǒng)自身數(shù)據(jù)及其他相關(guān)數(shù)據(jù)中挖掘出更多有價值的信息，為管網(wǎng)運行決策提供技術(shù)支持。

3）本文所提出的基于人工智能技術(shù)的管道系統(tǒng)可靠性計算方法，可以逐步與基于物理機理的在線仿真工藝預測結(jié)合，將能夠自動預測天然氣管網(wǎng)未來工況（如資源及銷售、關(guān)鍵節(jié)點壓力及用戶用氣量等），探索管網(wǎng)在安全約束下的智能運行，為中國管道行業(yè)最終實現(xiàn)有監(jiān)督條件下的自適應運行提供安全監(jiān)測、預測等方面的技術(shù)支持及保障。