借概念構圖 促整體建構

何葉飄 黃鼎滴

【摘? ?要】整理與復習課可以幫助學生加深對知識的理解，實現知識系統化。以《因數與倍數》整理與復習課為例，闡述以概念構圖為抓手引導學生對“因數與倍數”單元的內容進行整理，通過整理進一步理解相關概念的意義、明確概念的內涵和外延，并厘清概念間的層級關系。

【關鍵詞】概念構圖;思維;深度;整理復習

整理與復習課主要有兩個目標，即知識整理和鞏固提升。在整理與復習課上，要通過對知識間關系的梳理，點串成線，線連成面，幫助學生實現知識結構化、系統化。以往教師在進行“因數與倍數”單元的整理與復習時，通常先引導學生梳理歸納知識點，形成結構，然后以不同類型、不同層次的練習為載體，通過訓練、講評來檢測學生對知識的掌握情況。但這一單元教學內容中，涉及的概念數量多，概念比較抽象，概念間的關系復雜，導致學生整理時容易出現混亂現象。針對這種現狀，筆者嘗試以“概念構圖”為教學途徑，引導學生在合作構圖中不斷修正、完善概念理解，進一步明晰概念之間的內在關系，提高理解水平和應用能力，實現深度學習。

一、初構概念圖，呈現已有經驗

為更好地了解學生對于因數、倍數知識掌握的情況，教師請學生回憶“關于因數和倍數，你能想起哪些知識點”，思考“這些知識點之間有什么聯系”，并在導學單上繪制概念圖。學生在這一過程中，會充分暴露已有的認知狀態。教師通過整理學生的作品（如圖1～圖4）發現，學生的理解水平存在很大的差異。

從以上作品中可以看出學生的三個理解水平層次。

理解水平1：作品1和作品2都是從“數”這個主干生長出“奇數、偶數”“質數、合數”“公因數”“公倍數”和“互質數”等分支。這部分學生只是對知識點進行了簡單的羅列，層級關系不清晰，知識結構較低。因此我們把它們定位為理解水平1。處于這一水平層次的學生占全班總人數的22.2%。

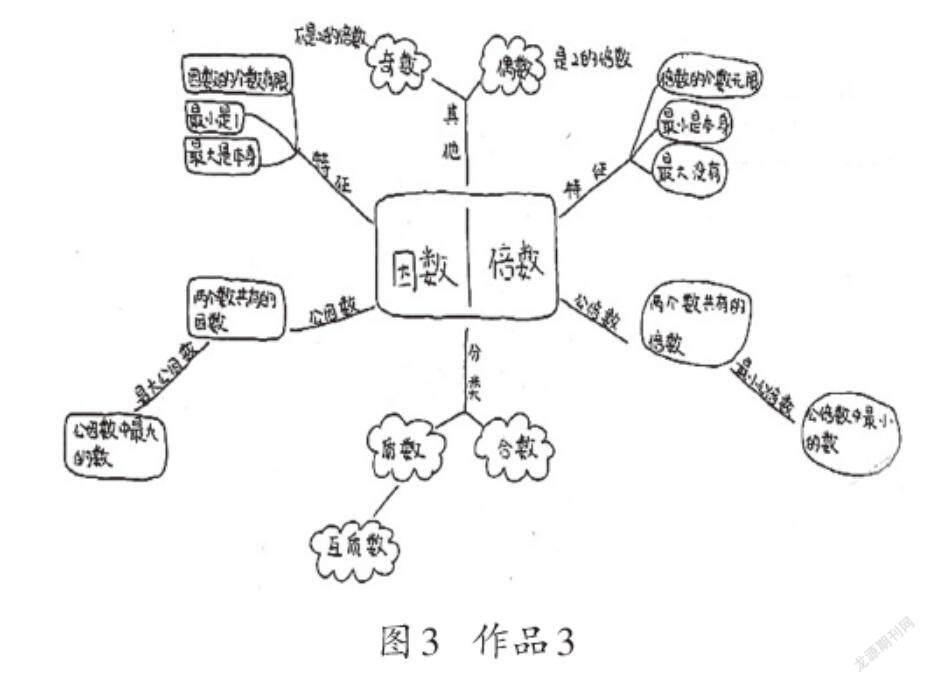
理解水平2：從作品3可以清晰地看出“因數、倍數”是一級概念，“奇數、偶數”“質數、合數”是從屬于“因數、倍數”的二級概念，有一定的層級關系。雖然有些層級關系表達得還不夠清晰，但對比作品1和作品2，已經高了一個水平，我們把它定位為理解水平2。處于這一水平層次的學生占全班總人數的71.1%。

理解水平3：作品4不僅能清晰地表達不同維度的知識，而且有序地建構了各個概念之間的層級關系，并能準確地表達“因數和倍數”是相互依存的關系。處于這一水平層次的學生較少，只占全班總人數的6%。

由此可以看出，學生對“因數與倍數”單元中涉及的知識點都能一一羅列，但缺乏概念間的內在關系的梳理，只有小部分學生能厘清概念間的層級關系。因此在教學中教師要對學生已有認知進行深度剖析，強化對零碎概念的整理與關聯。

二、評論概念圖，經歷深度辨析

教師選擇作品3作為主要討論對象，引導學生進行論圖辨析。

1.教師出示問題一：你能看明白作品3嗎？你看明白了什么？請學生討論。

生：我能清晰地看到因數和倍數的特征，最大的因數是其本身，最小的倍數也是其本身。

生：我發現在“因數與倍數”的相關知識中有很多概念，這些概念存在著一定的聯系。

2.教師出示問題二：這些概念之間的層級關系是否合適？如果不合適，你會怎么調整？請學生討論。

生：我覺得質數和合數應該放在因數的層級之下，因為根據因數的個數，可以把非零自然數分成質數、合數和1，作品3的作者把1漏了。

生：我還有補充，質數和互質數是不一樣的，質數是根據因數的個數來判定的，它是一個數。互質數是根據公因數的個數來判定的，它是兩個數之間的一種關系。所以，互質數應該在公因數的層級之下。

生：我還有點想法，我覺得奇數和偶數應該放在倍數的層級之下，因為奇數和偶數是根據“2的倍數特征”來判定的。

生：我有不同意見，奇數和偶數也可以放在因數的層級之下，因為可以根據有沒有因數2來判定奇數和偶數。

……

之所以選擇作品3展開討論，首先是因為它代表著大部分學生的理解水平。用它來引導學生展開討論和思辨，具有一定的普適性，容易激發學生的學習積極性和主動性。其次是因為作品3里有比較適合激發學生思辨的切入點，學生思維生長的空間比較大。比如“奇數、偶數”這兩個概念，學生把它們放在“因數與倍數”總概念之下，連接詞是“其他”，就說明他對“奇數、偶數”應該放在哪個層級之下并不清楚。因此在課堂中，應緊扣學生的認知困惑點，讓學生在交流、辨析、調整的過程中，不斷理解“奇數、偶數”與“因數、倍數”概念之間的關系。厘清了這些概念之間的層級，也就厘清了各個概念之間的區別與聯系。另外，我們也從作品3中發現，學生對“質數”和“互質數”這兩個概念的理解比較模糊。“質數”與“互質數”之間的辨析，需要透過表象看本質，因此可以通過質疑與釋疑來促進學生深入理解它們的意義。

在交流過程中，學生以圖為介，邊觀察邊思辨，在思維碰撞中形成深度的理解。學生有的從概念定義的角度對“質數”和“互質數”進行了辨析;有的拓寬了對“奇數、偶數”由來的再認知，啟發其他同學感悟“如何從不同視角把握知識間的關系”。通過這樣的過程，學生不再簡單地從字面上理解數學概念，而學會進一步溝通概念之間的聯系，以此來深入理解概念的意義。

三、重構概念圖，完善認知建構

學生掌握了“因數與倍數”的相關知識及內在關系后，還需要在理解的基礎上通過反思進行重構，以達到內化提升的目的。因此在這個環節安排了兩個學習任務：（1）在小組內交流各自的收獲和思考。（2）以小組為單位重構“概念圖”。

在小組合作中，學生可以從構圖的形式和理解的內容兩個維度出發，通過比較、思辨、修正、完善等數學活動，達成共識，形成層級關聯清晰的知識結構。這是數學內化的最好表現，也是學生學會表達、強化理解的有效途徑。

通過這樣一個重構的過程，學生對奇數與偶數的處理進入“柳暗花明又一村”的境界。有些學生把質數和合數放在了因數個數有限的特征之下，可見他們對質數和合數已經有了正確的個性化理解。這個過程讓學生不再把這些概念理解成“數”，而是明白了它們的本質意義，并建立了符合自己認知特點的層級關系。學生的理解從“散亂”走向了“結構”，從“表層”走向了“深刻”。

實踐證明，學生經歷了“初構概念圖—評論概念圖—重構概念圖”的過程，就會自主產生很多新的感悟，形成一些更深刻的數學理解。可見，概念構圖在整理與復習課中的運用是有效的，值得應用推廣。但需要強調的是，教師在組織教學時至少要做到以下三點：一是遵循學生“從發散思維到結構思維”的學習導向來進行教學;二是加強“思維可視”為“理解進階”服務的意識;三是把握“求同存異”與“深層關聯”的教學價值。相信唯有如此，概念構圖在整理與復習課中的運用才會喚醒學生的數學思維活力，有效提升他們的數學理解水平，為實現“輕負高質”提供可行路徑。

參考文獻：

[1]吳亞子.概念構圖：一種有效的學習策略[J].教育實踐與研究，2006（5）.

[2]顧健.深度教學視角下的小學數學理解性教學策略[J].新課程研究，2020（31）.

（1.浙江省東陽市白云甘井小學? ?322100

2.浙江省東陽市吳寧第五小學? ?322100）6741614D-75DD-44F3-9846-2C292CA3A3AB