橢圓余弦波對外圓弧透空薄壁雙圓筒柱的繞射*

黃坤輝，黃華，詹杰民，才瀚濤

中山大學航天航空學院應用力學與工程系，廣東 廣州 510275

直立圓柱是近海離岸建筑支撐結構的重要形式之一，剛性圓弧型薄壁則為用于抵御波浪作用的各類防波堤中的典型而簡便的結構形式之一。外圓弧透空薄壁內接圓柱構成了一種新型的海工典型組合結構，其中外接單一或不同圓心角雙層圓弧薄壁可直接提供對內接圓柱的防護，也可由其演化出多層透空圓環柱或單層圓弧堤內接圓環柱等多種海工結構，因此對其展開與波浪相互作用問題的理論研究意義十分重大。Wiegel［1］計算了半無限長薄壁直立防波堤的水波繞射問題。Losada 等［2］解析研究了斜入射線性波浪對三種不同類型直立薄板的波浪力及繞射波面。張芹等［3］用實驗方法分別研究了規則波和隨機波浪對開口直立墻和不開口直墻波浪作用力。程建生等［4］和楚玉川等［5］各自解析分析了單一圓弧型防波堤的Airy 波防浪效果和對應的波浪力。 此外，Chwang［6］推導了微幅波與透空直墻的相互作用解析解，計算了透空直板造波器上的波浪力。Darwiche 與Williams 等［7-8］對內圓柱外接圓柱型透空防波堤結構的波浪繞射展開了理論計算。Williams等［9］給出了微幅波對透空浮筒繞射的理論公式。劉俊和林皋［10］應用比例邊界有限元法，對微幅短峰波與圓柱外接圓弧開孔結構物的相互作用進行了數值研究。林皋和劉俊［11-12］應用同樣的數值方法模擬了Airy 波對雙層圓弧型貫底式開孔介質防波堤以及圓柱外接同圓心角雙層防波堤的繞射。

防波堤及其所保護的柱體結構主要設置在近岸水域。在淺水區，水波一般呈現非線性淺水波特征，一定條件下需要引入橢圓余弦波的淺水波模型加以研究。Issacson［13］首先給出了一階橢圓余弦波對單立大尺度圓柱繞射的解析理論；邱大洪［14］據此對橢圓余弦波作用于大尺度單柱的繞射波面分布進行了預測；Weng等［15］推廣Airy波的柱群算法解析計算了橢圓余弦波一階分量與透空圓環柱群的波浪力及爬高；張敖等［16］計算了橢圓余弦波對單一圓弧型防波堤的波浪作用。本文選取不同圓心角雙層圓弧型透空薄壁內接圓柱這一經典的海工可變組合結構，引入淺水波中的橢圓余弦波一階分量理論，對該結構的淺水波繞射問題展開了解析研究。

1 橢圓余弦波對外接圓弧透空薄壁之圓柱組合結構繞射的一階波勢解

設在均勻水深為d的海域中有半徑分別為a和b的外層與內層圓弧透空薄壁，以及半徑為c的內圓柱的組合結構，如圖1所示。外層與內層薄壁透空系數分別為G1和G2。坐標平面Oxy置于水底，原點置于圓心處，設置外層透空薄壁關于Ox軸對稱，圓弧兩端點與原點連線同Ox軸正向夾角分別為θ1=α1，θ1= 2π -α1，外層壁對應的圓心角為γ1= 2π - 2α1，內層壁對稱位于θ2=α2至θ2=2π -α2間，內層壁對應的圓心角為γ2= 2π - 2α2。Oz軸垂直向上，斜入射橢圓余弦波一階分量與Ox軸正向夾角為β，波高與波頻分別為H和ω。以半徑a和b劃同心圓環柱面，流場由此劃分為外流域Ω0、內流域Ω1和Ω2。

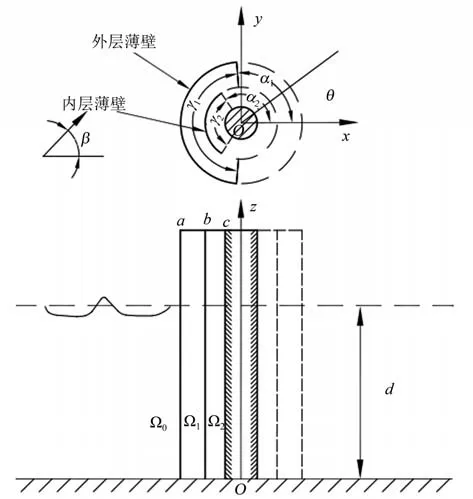
圖1 雙層外圓弧透空薄壁圓環筒柱結構Fig.1 Concentric cylindrical structure with double-layered arc-shaped porous outer thin wall

對于理想無粘流體，假定液體不可壓縮且運動無旋。設水波總速度勢Φ=Φi+Φs= Re(φ) =Re(φi+φs)，則有

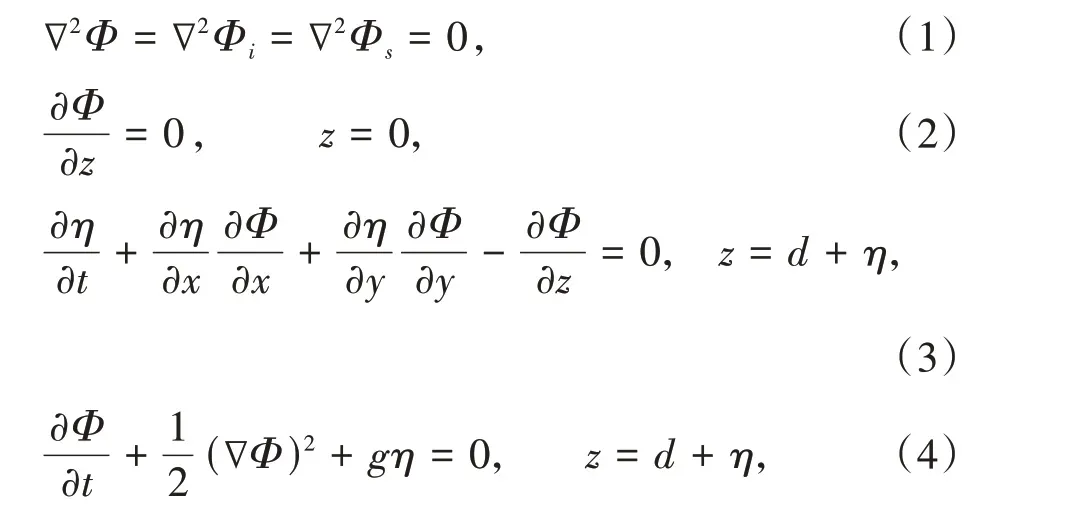
其中φi和φs分別表示入射波和散射波速度勢。另φ與φs須滿足結構表面條件與無窮遠輻射條件。

根據橢圓余弦波一階分量理論［13］，沿Ox軸方向入射的橢圓余弦波一階波勢可寫為

式中

由同心圓環柱物面及非物面處的邊界條件，參考文獻［17］可得系數求解公式

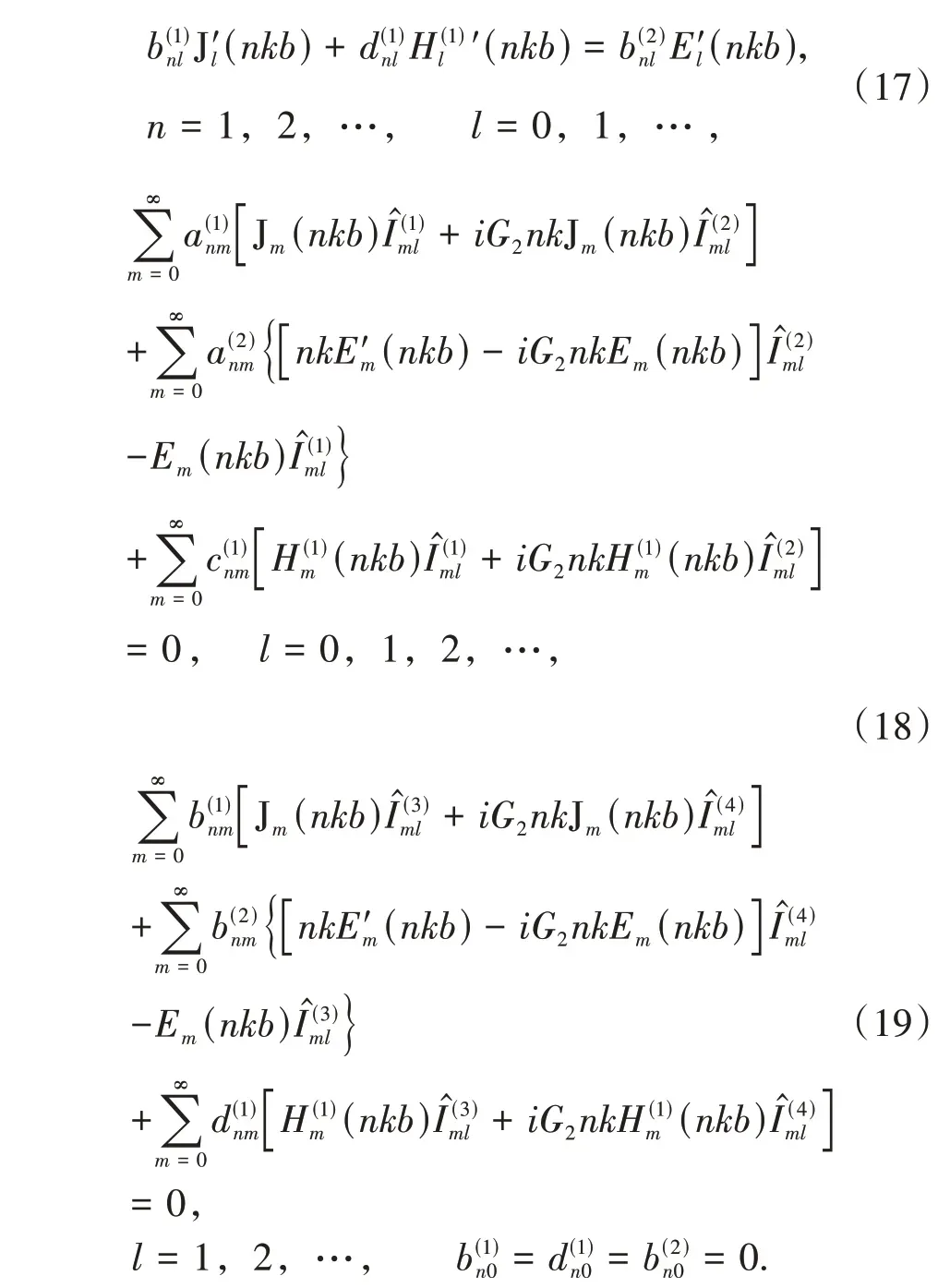
其中

各區波勢解待定系數可由式（12）～（19）進行聯立完備求解。在實際計算中，可根據精度要求進行截項運算。

對應區域Ωj的繞射波面η(j)和海水動壓強分別為

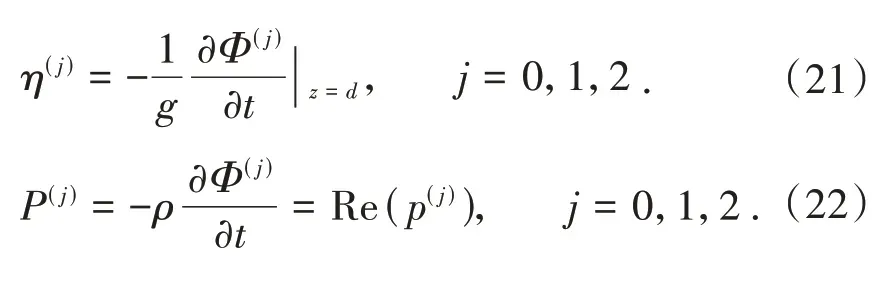
2 算例與分析

取內、外薄壁圓弧張角為360°，內圓柱半徑為c= 0，結構即化為單層透空圓環柱結構，再按文獻［17］同結構相同參數進行設置。圖2給出了單層透空圓環柱所受最大無量綱波浪力與文獻［17］對應值的比較結果。由圖可知，在相同參數下兩種不同波浪繞射解對同一圓環柱的無量綱最大總波浪力（內外柱合力）的預測結果完全吻合，說明本文所給雙層圓弧薄壁內接圓柱的橢圓余弦波一階繞射解是正確可靠的。

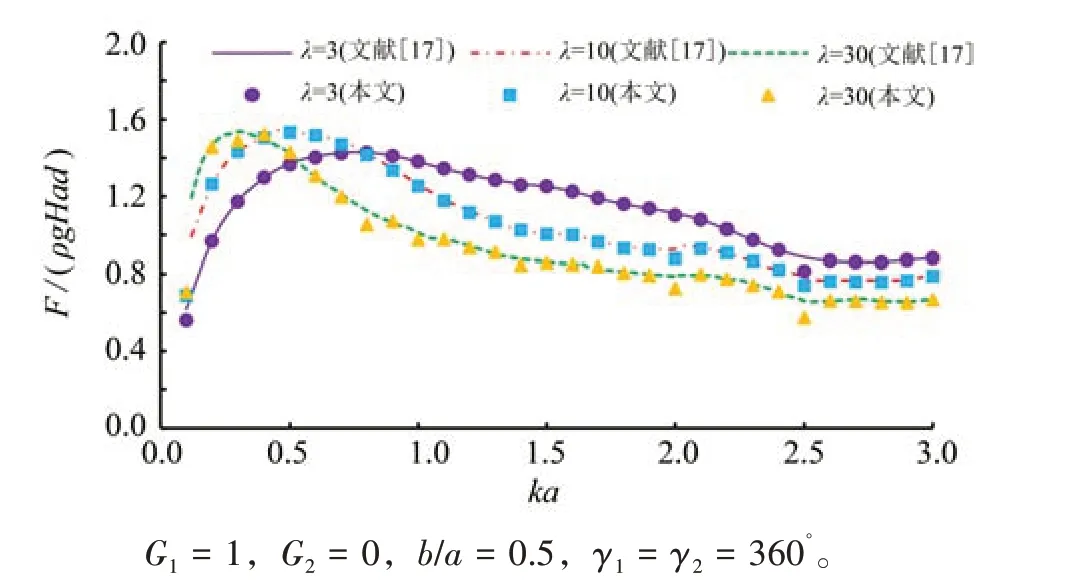
圖2 透空圓環柱的波浪力驗證Fig.2 The verification of wave forces on a porous circular annular cylinder

圖3為單、雙層圓弧薄壁內接圓柱與單一同徑密實圓柱的最大無量綱波浪力的比較結果。其中單層壁情形對應外圓弧壁張角取120°，內圓弧壁張角為0°，此時結構化為單層圓弧透空薄壁內接密實圓柱。

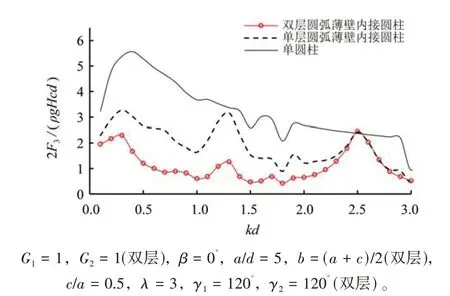
圖3 單、雙層壁內接圓柱保護效果的比較Fig.3 Comparison of protection effects of inscribed cylinder with single-layered arc-shaped outer thin wall and double-layered arc-shaped outer thin walls

由圖可見，單一圓柱的無量綱波浪力幅值最大，單層圓弧薄壁內接圓柱的對應值次之，而雙層圓弧透空薄壁內接圓柱的對應值最小。單、雙層圓弧薄壁使其內接圓柱所受最大無量綱波浪力較單一圓柱對應值最大分別可減小58%和83%，說明外置透空圓弧薄壁可以大幅度降低內圓柱的承載，其中雙層壁降載效果更為明顯。

內、外層薄壁不同透空系數組合形式下，雙層圓弧透空薄壁內接圓柱組合結構的最大無量綱波浪力如圖4所示。透空形式包括：外壁和內壁均密實，外壁密實內壁透空，外壁透空內壁密實以及外壁內壁均透空四種。由圖可知，采用外壁與內壁均密實的結構形式將導致內、外壁以及內圓柱結構的無量綱波浪力幅值在kd較小時（kd＜0.5）隨kd的變化曲線均出現較大振蕩。而外壁密實內壁透空時外壁曲線與雙壁均密實振蕩形態相似。同樣，內壁密實外壁透空時內壁曲線與雙壁均密實振蕩形態相似且波浪力幅值的振蕩幅度與最大值更大。當kd＜0.5 時，外壁與內壁之一密實或均密實時內柱對應曲線呈現振蕩形態且波浪力幅值整體較大。外壁與內壁均透空時內柱的對應曲線隨kd變化相對平緩且無量綱波浪力幅值平均而言減小。內外壁自身的透空也將一定程度降低它們自身結構的波浪力幅值并明顯平緩振蕩態勢。對比四種不同透空組合形式，從三個結構各自波浪力幅值角度考慮，采用雙壁均透空的結構形式較為合適。

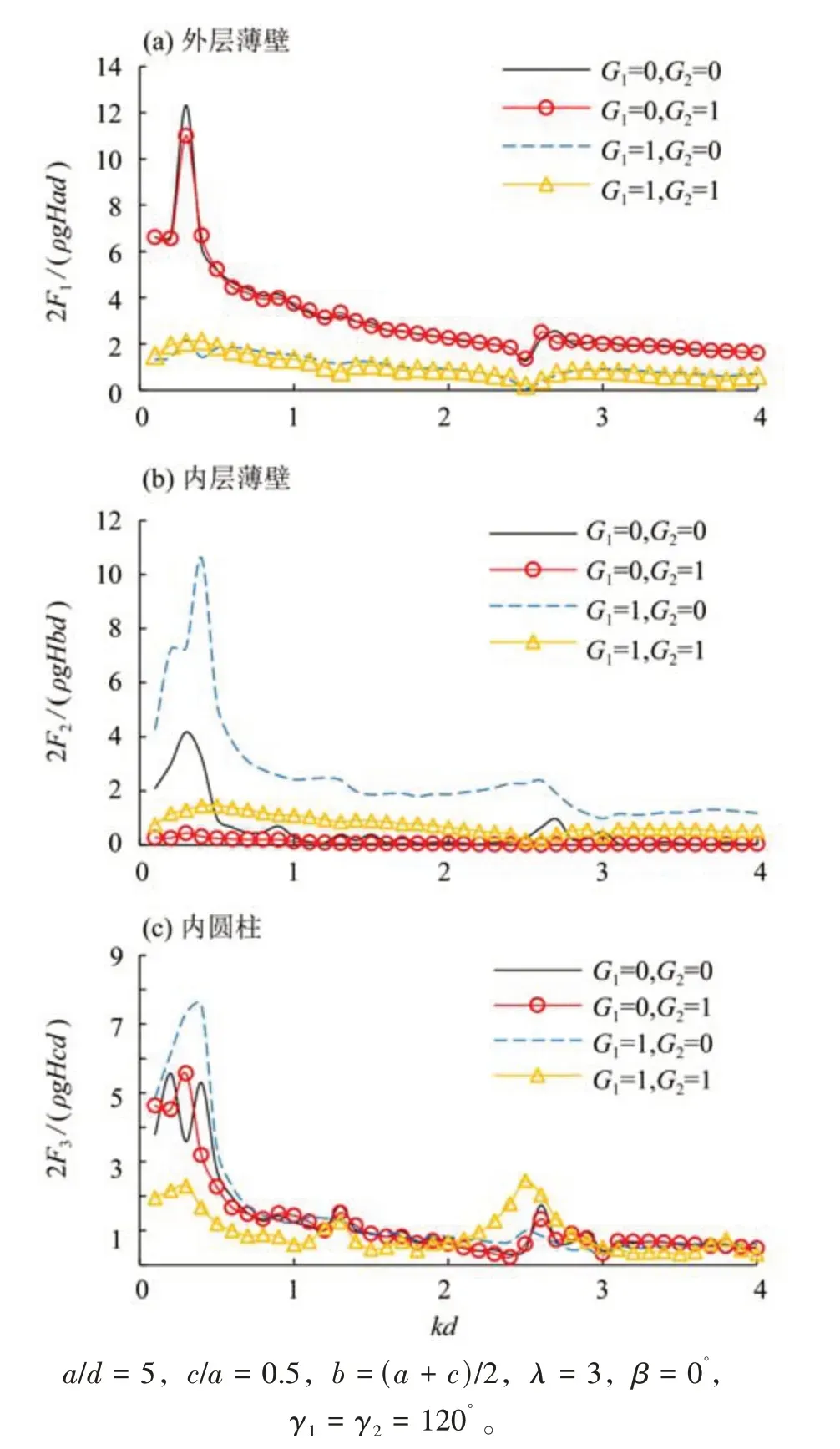
圖4 不同雙壁透空系數下組合結構的波浪力Fig.4 The wave forces on combined bodies at different porous coefficients of double-layered walls

圖5 為波浪入射角β對雙層圓弧透空薄壁內接圓柱組合結構的最大無量綱波浪力的影響趨勢。由圖可見，當kd＜2時，波浪入射角越大，內、外層薄壁無量綱波浪力幅值越小，相反內圓柱的對應值越大。現設內、外層薄壁張角均等于γ，圖6為γ不同時組合結構最大無量綱波浪力隨kd的變化趨勢。由圖可知，當kd＞0.5 時，內、外層薄壁張角γ變化對組合結構各部分的波浪力幅值均影響較小。當kd＜0.5 時，隨著張角γ的減小外壁與內壁的無量綱波浪力幅值隨之減小，而內圓柱的對應值有所增加。

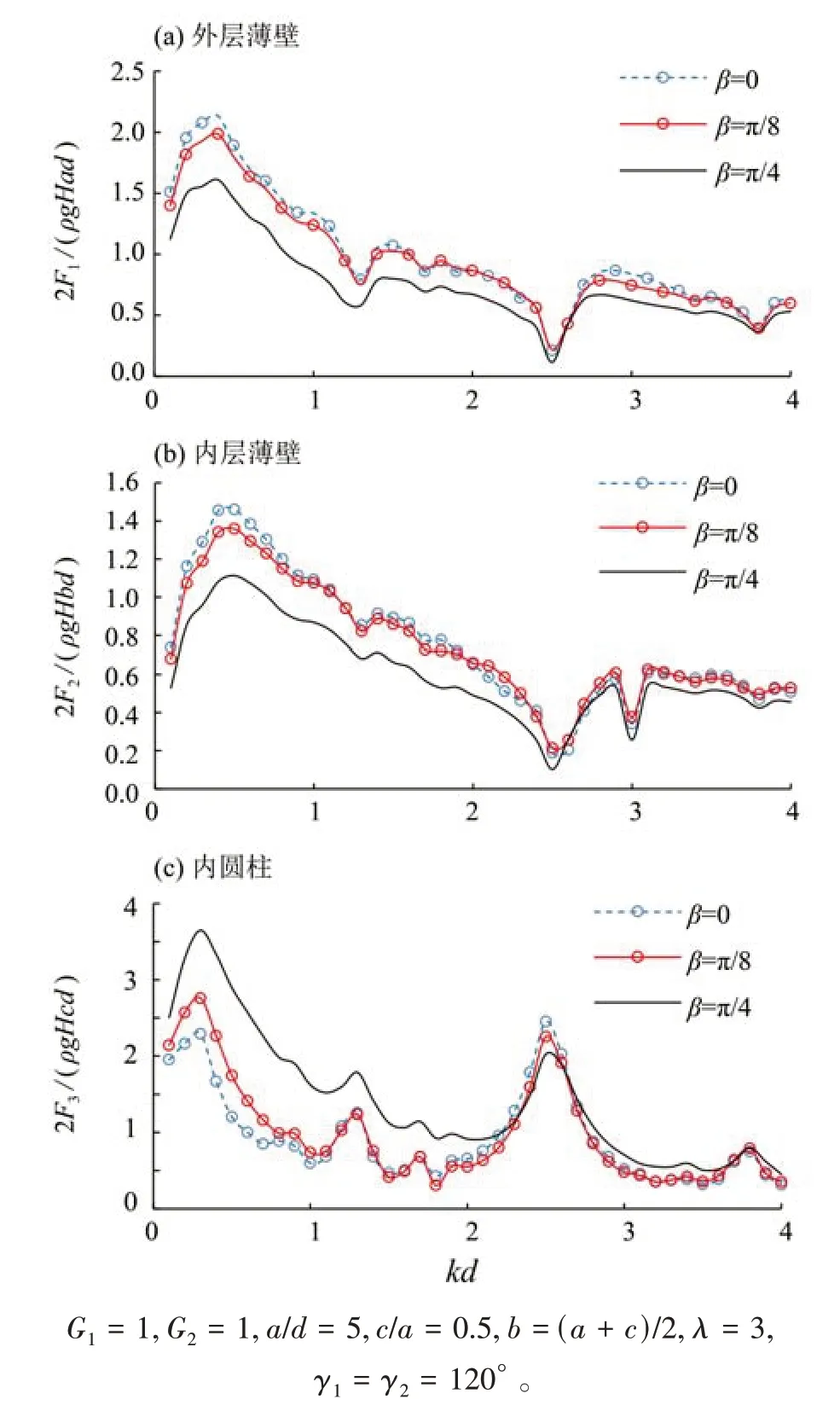
圖5 不同入射角β下最大無量綱波浪力隨kd的變化Fig.5 The variation of maximum dimensionless wave forces with kd at different incident wave angle β

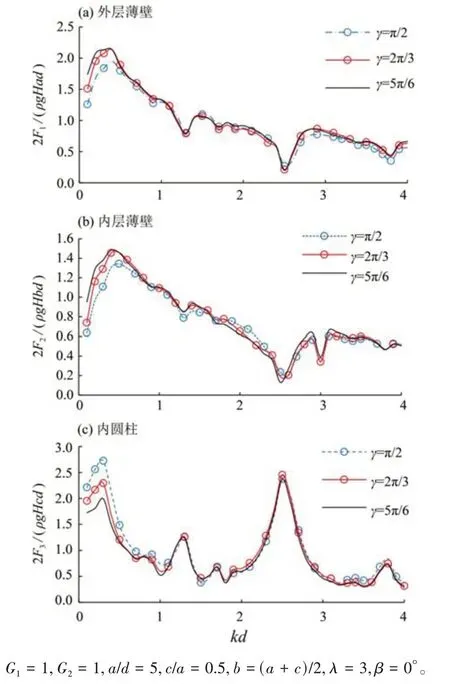
圖6 不同張角γ下最大無量綱波浪力隨kd的變化Fig.6 The variation of maximum dimensionless wave forces with kd at different central angle γ

進一步設內層薄壁張角γ2= 120°保持不變，圖7為外壁張角γ1不同時組合結構最大無量綱波浪力隨kd的變化趨勢。由圖可知：內壁無量綱波浪力幅值基本不隨kd變化。外壁的對應值僅當kd＜0.5 時隨著外壁張角的減小而略微減小，同時內圓柱的對應值略有增加。這說明在雙層薄壁設計中可選擇較小外壁張角的外壁以明顯減小外壁弧長而節省建造成本，而此方案對組合各結構的對應承載均影響較小。

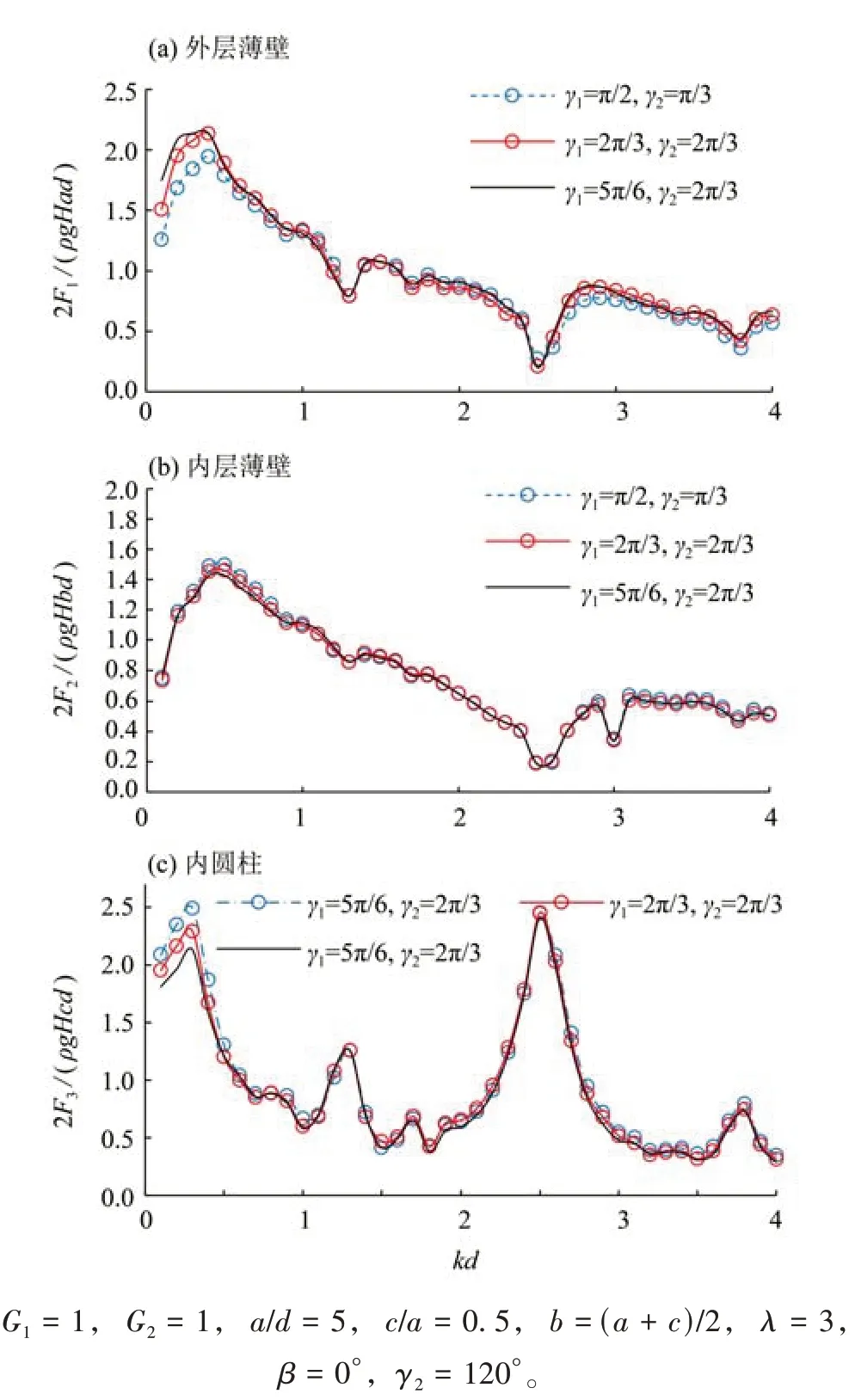
圖7 不同薄壁張角γ1下最大無量綱波浪力隨kd的變化Fig.7 The variation of maximum dimensionless wave forces with kd at different central angle γ1

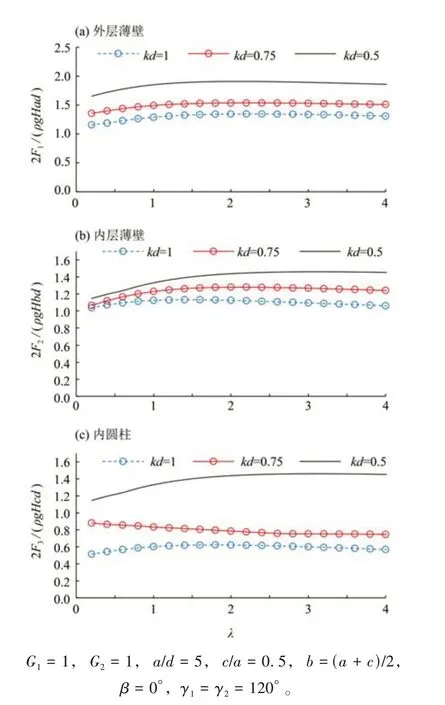
圖8 不同kd下最大無量綱波浪力隨特征參數λ的變化Fig.8 The variation of maximum dimensionless wave forces with characteristic parameter λ at different kd

圖9為相同條件下橢圓余弦波一階繞射理論與微幅波繞射理論對雙層圓弧透空薄壁內接圓柱組合結構波浪力幅值的比較。對比圖中曲線可知，相較微幅波波浪模型，利用非線性波浪模型計算波載的方法所得無量綱波浪力更大，再考慮淺水波的實際波高必然大于微幅波值，則非線性波的實際最大波浪力必然大于微幅波值。這說明在淺水工況下，運用本文方法所給結果相對更加可靠。

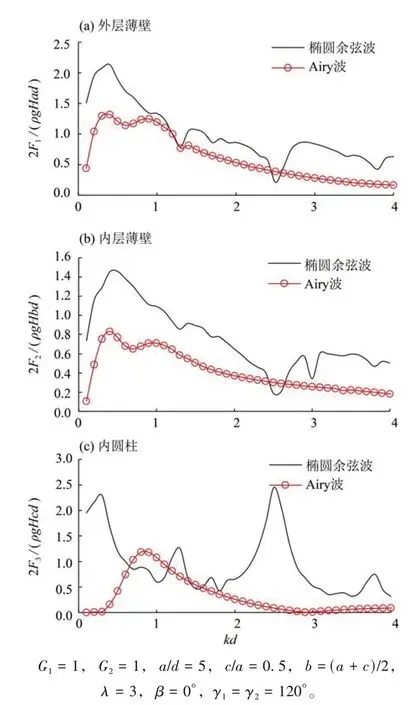
圖9 不同波型作用于組合結構的波浪力對比Fig.9 Comparison of wave forces on combined bodies given by different wave theories

圖10 為橢圓余弦波與淺水條件下微幅波對雙層圓弧薄層內接圓柱繞射的最大無量綱波面分布剖面(y= 0)比較。由圖可見，橢圓余弦波對最大波面值的預測值整體大于Airy 波理論的計算值。外流域、中層流域及內流域分別在外層薄壁、內層薄壁和內圓柱的前壁面處出現相應流域內的最大波面峰值，其值分別為Airy 波對應值的1.8 倍、1.8 倍和3.5 倍。該結論再次表明：在一定的淺水條件下，橢圓余弦波模型因考慮了淺水波綜合影響因素，其對波浪作用的估算更為安全可靠。

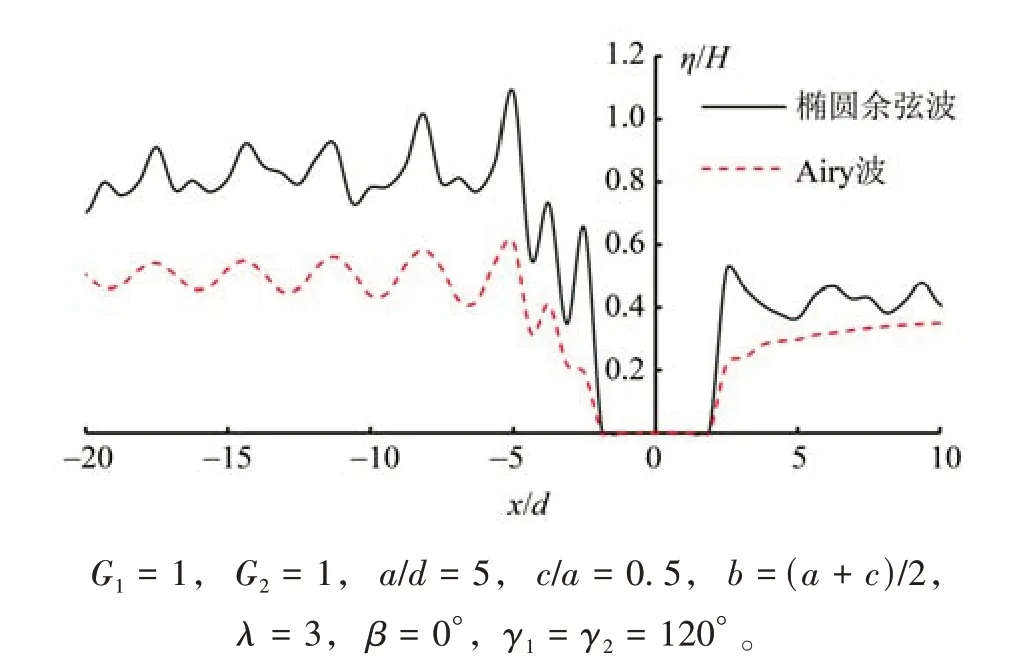
圖10 不同波型作用于組合結構產生的最大波面剖面Fig.10 Comparison of maximum wave elevations of different waves acting on the combined structure

取外圓弧張角為120°，內圓弧張角為0°，組合結構化為單層圓弧透空薄壁內接密實圓柱結構。圖11 為單、雙壁內接圓柱結構在橢圓余弦波作用下產生的最大繞射波面分布截面對比。結果表明：由于外圓弧透空薄壁對入射波浪的直接遮攔作用，相較于雙層結構，單層結構內圓柱表面的最大波浪爬高以及內圓柱前鄰近的最大波幅均有明顯降低，較好地體現了外層圓弧薄壁對中心區圓柱的防浪保護作用。

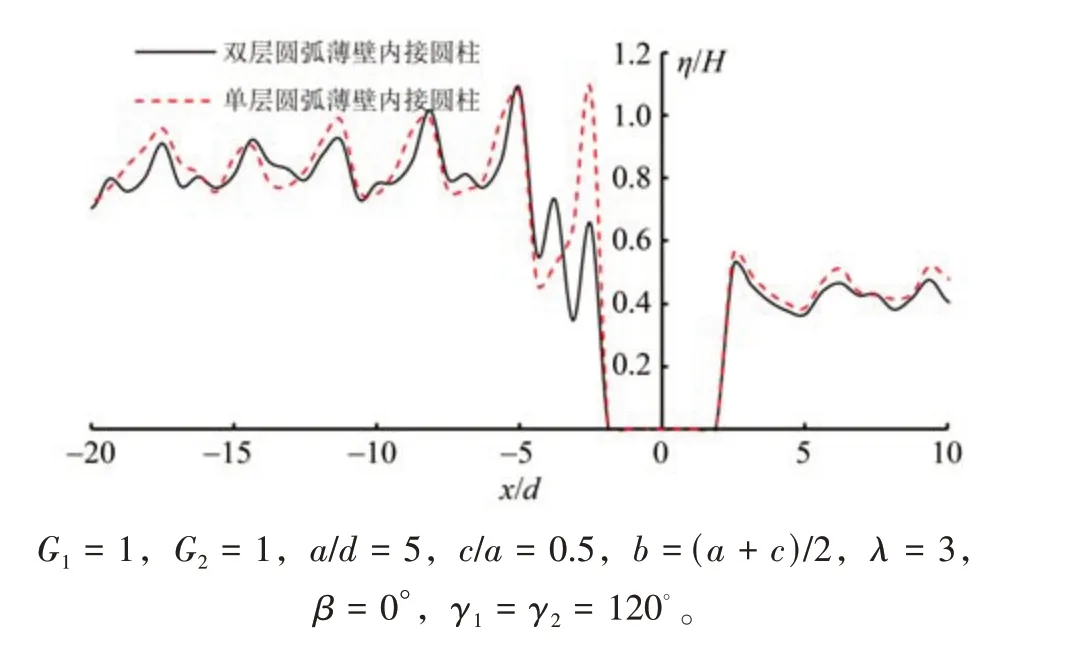
圖11 波浪作用于不同組合結構的最大波面的剖面Fig.11 Comparison of maximum wave elevations distribution around different combined structures

圖12 為單層或雙層壁內接圓柱與單一圓柱表面最大波浪爬高的比較。結果表明：由于薄壁對波浪的遮攔作用，單、雙層圓弧薄壁內接圓柱最大波浪爬高較單一圓柱對應值明顯減小，且雙層圓弧薄壁內接圓柱的最大波浪爬高較單層薄壁情形的對應值更小。

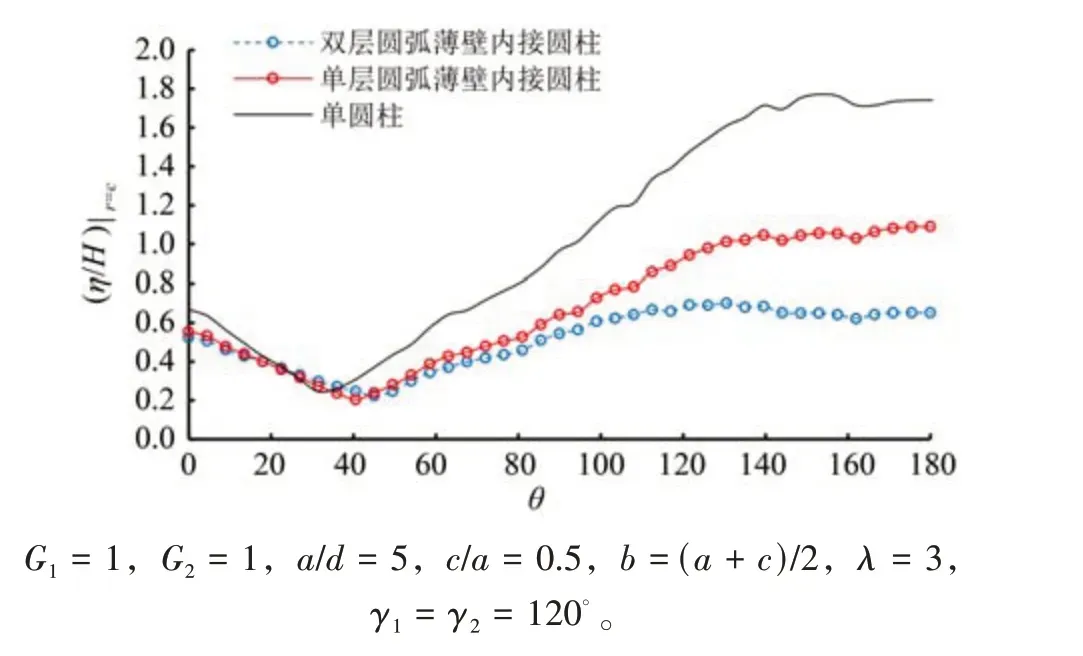
圖12 透空薄壁之內接柱與單柱波浪爬高的對比Fig.12 Comparison of wave run-ups on a single cylinder and inscribed cylinder with single or double-layered arc-shaped outer thin walls

3 結 論

本文給出了橢圓余弦波一階分量對不同圓心角雙層透空薄壁內接圓柱繞射的解析理論，從而在波浪類型、結構類型以及研究方法類型上均進行了有效拓展，主要結論包括：

1）應用本文理論和已有的透空圓環柱淺水波繞射解進行了實算比較，結果良好。

2）本文方法所預測的最大波浪作用均大于同等淺水條件下微幅波模型的對應結果，說明此方法具有一定的可靠性與實用價值。

3）相比單一圓柱，單、雙層薄壁的設置可以有效減小內接圓柱所受到的最大波浪載荷與圓柱表面的最大波浪爬高，其中雙層壁較單層壁對圓柱波浪作用的降低效果更為明顯。

4）適當選擇張角較小的外層圓弧薄壁可縮短外堤長度而節省成本，且對組合結構的波載影響不大。

5）采用外壁和內壁均透空的結構組合形式對降低內外層薄壁以及內柱的最大波載相對有利。

6）淺水波入射角、薄壁張角、雙層壁透空系數以及波浪要素等均一定程度地影響波浪對組合結構的繞射作用。組合結構的橢圓余弦波實際最大波浪力隨淺水波特征參數的增加而增加。