非線性磁懸浮轉子系統的不平衡響應分析
劉明政,葛萍萍, 張雁翔, 姚俊夫,王念先
(1.武漢科技大學 機械自動化學院,武漢 430081;2.冶金裝備及其控制教育部重點實驗室,武漢 430081;3.韶關液壓件廠有限公司,廣東 韶關 512000)
主動磁懸浮軸承是一種通過可控電磁力使轉子穩定懸浮的軸承,具有無接觸、無潤滑、無磨損、轉速高和動態特性可調等優點,應用越來越廣泛[1]。在高轉速下轉子不平衡會對系統產生較大破壞,是系統故障的主要因素。當磁懸浮轉子系統在復雜工況下工作時,磁性材料相對磁導率變化明顯,磁懸浮軸承非線性支承特性顯著增加,轉子不平衡對系統的影響更復雜,需要進行研究。
磁懸浮軸承非線性支承特性主要由系統漏磁、磁飽和等因素造成[2]。在漏磁方面:文獻[3]考慮氣隙漏磁,提出了一種新型永磁偏置軸向混合磁懸浮軸承,使其具有較低的功率損耗與良好的控制性能;文獻[4]針對新型徑向混合磁懸浮軸承,利用等效磁路法建立數學模型計算漏磁系數,并通過試驗和有限元法驗證了模型的正確性;文獻[5]基于ANSYS和試驗建立混合磁懸浮軸承非線性支承力模型,提高了大氣隙混合磁懸浮軸承承載力計算精度。在磁飽和方面:文獻[6]建立考慮磁飽和影響的磁懸浮軸承非線性支承力模型,試驗證明該模型更精確;文獻[7]考慮磁飽和影響,基于磁路法建立考慮漏磁及磁飽和等因素的磁懸浮軸承非線性支承力模型,該模型在不同的氣隙長度與偏心距下計算精度均較高。
在磁懸浮轉子系統不平衡響應方面:文獻[8]建立剛性磁懸浮轉子動力學模型,分析了控制參數對轉子模態的影響,得到轉子渦動擺振頻率隨控制參數的變化規律;文獻[9]對磁懸浮轉子系統穩態不平衡響應進行分析,不同轉速區域采用不同的磁懸浮軸承控制參數,可改善系統動態特性;文獻[10]建立主動磁懸浮電主軸系統動力學模型,分析結構參數、控制參數對系統動態特性的影響,系統響應非線性特征顯著,且控制參數對系統響應影響更大。
上述磁懸浮軸承支承模型大多基于常規支承力模型,缺乏基于磁懸浮軸承非線性支承特性(考慮漏磁、磁飽和等非線性因素)的磁懸浮轉子系統不平衡響應分析。 鑒于此,建立非線性支承磁懸浮轉子系統模型,基于有限元法建立系統動力學模型,分析運行參數和控制參數對系統不平衡響應的影響。
1 非線性支承磁懸浮轉子系統模型
1.1 磁懸浮轉子系統結構
磁懸浮轉子系統結構如圖1所示,轉子主要結構參數為:長度580 mm,外徑25 mm,內徑15 mm,圓盤主要結構參數為:厚度27.3 mm,外徑250.0 mm,內徑25.0 mm,徑向主動磁懸浮軸承主要參數見表1,圓盤連接在空心轉軸上,轉軸由兩端磁懸浮軸承支承。基于有限單元法可將該系統離散成5個節點,為方便分析,做如下假設:1)僅考慮徑向振動的影響;2)圓盤為剛性圓盤,可用集中質量塊單元表示;3)忽略轉子重力對系統的影響。
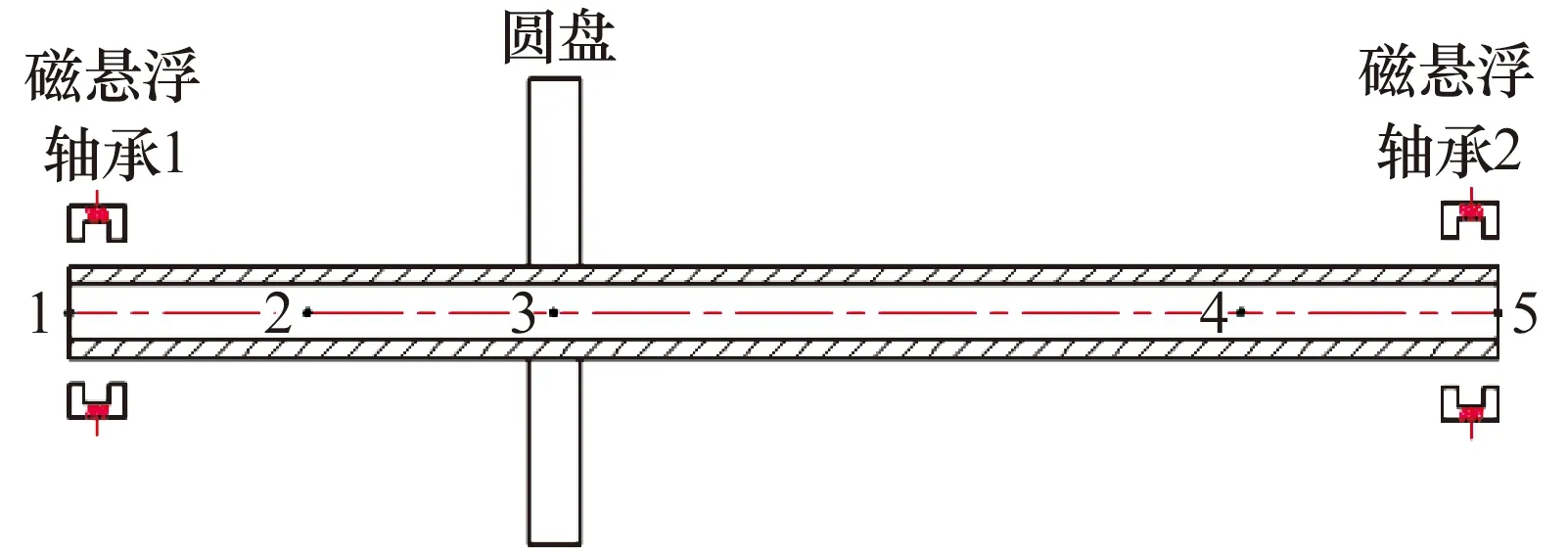
圖1 磁懸浮轉子系統結構簡圖Fig.1 Structure diagram of magnetic levitation rotor system
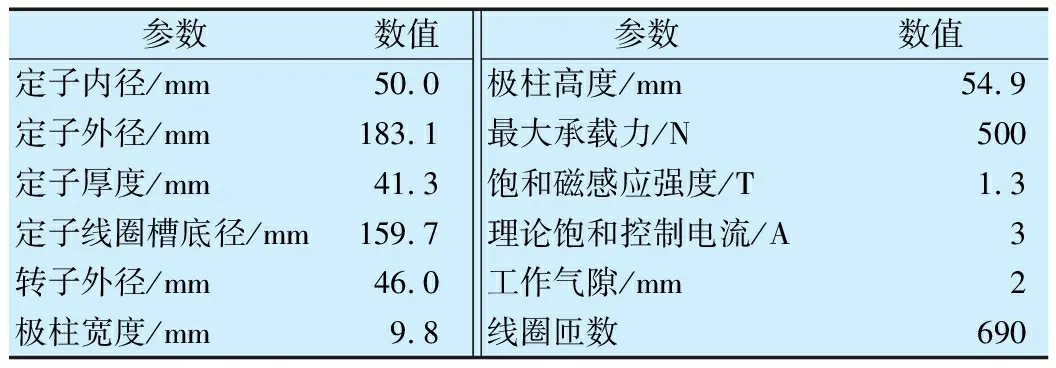
表1 徑向主動磁懸浮軸承主要參數Tab.1 Main parameters of radial active magnetic bearing
1.2 磁懸浮軸承支承力模型
采用差動控制的八磁極徑向磁懸浮軸承的結構及控制原理如圖2所示,圖中:F1,F2為線圈磁動勢,Ib為偏置電流,Ix為控制電流;g0為氣隙長度。
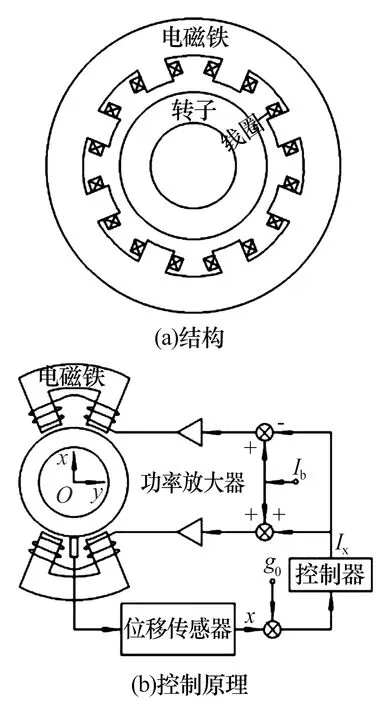
圖2 八磁極徑向磁懸浮軸承結構及控制原理圖Fig.2 Structure and control principle diagram ofeight pole radial magnetic bearing
忽略鐵磁材料的磁場耦合、渦流和磁滯的影響,為考慮漏磁及磁飽和等非線性因素的影響,可將磁場分布等效為磁路,采用場路結合法[8]劃分氣隙磁場、漏磁磁場,建立各磁路模型并得到總磁導或磁阻。通過冪函數擬合軟磁材料磁感強度-磁場強度(B-H)曲線,確定磁飽和影響下的磁極、磁軛和轉子磁阻值。氣隙磁通、漏磁模型如圖3所示,軟磁材料B-H曲線如圖4所示[8]。徑向磁懸浮軸承單個磁極的等效磁路圖(Equivalent magnetic circuit,EMC)如圖5所示,圖中:Ry,Rp,Rr分別為定子磁軛、磁極和轉子磁阻,Rk為漏磁磁阻,Rg1,Rg2為磁極處氣隙磁阻。
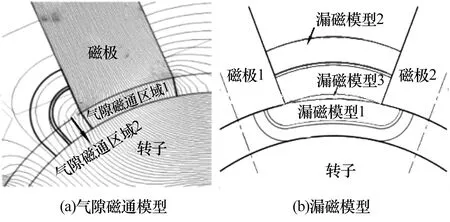
圖3 磁路模型Fig.3 Magnetic circuit model
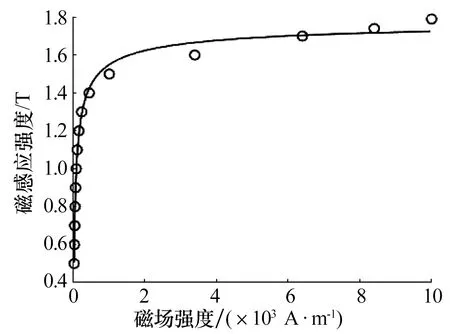
圖4 軟磁材料B-H曲線Fig.4 B-H curve of soft magnetic material
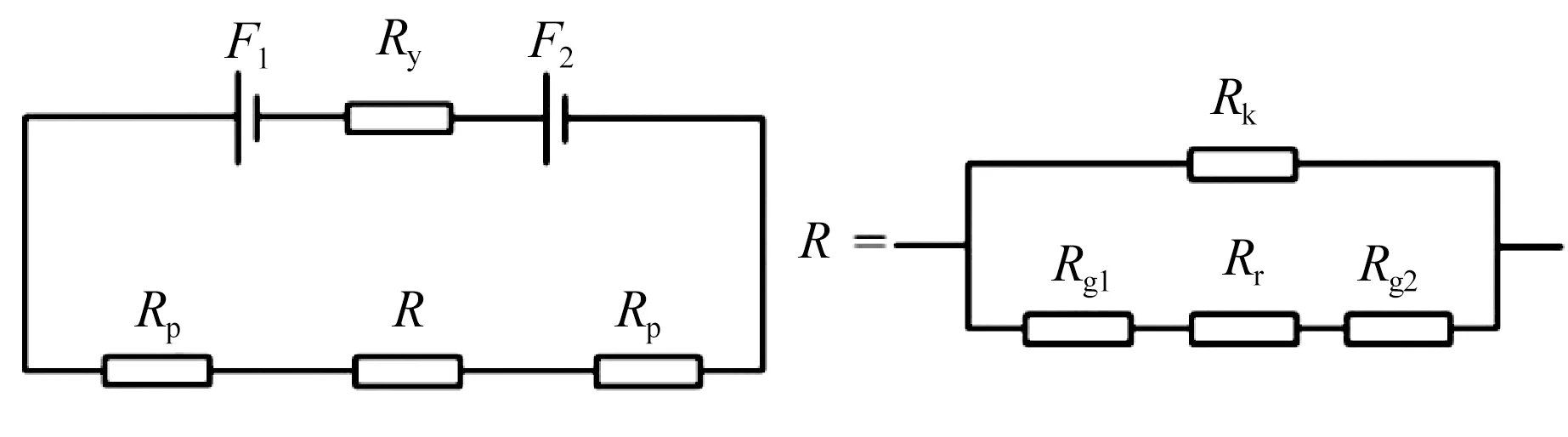
圖5 單個磁極的等效電路圖Fig.5 Equivalent circuit diagram of single magnetic pole
x方向兩磁極對作用下的非線性支承力為
(1)
Φ1=
Φ3=
式中:α為磁極對夾角的一半;μ0為真空磁導率;Ap為磁極面積;Ф1,Ф3分別為兩側通過磁路氣隙中的磁通;N為線圈匝數;Rg3,Rg4為磁極處氣隙磁阻。
采用有限元軟件驗證支承力模型[5],當轉子偏離平衡位置(偏移距離與氣隙長度的比值為0.2),氣隙長度g0=2.0 mm時,轉子承載力如圖6所示,負載較大時,常規支承力模型誤差較大,而非線性支承力模型具有較高精度。
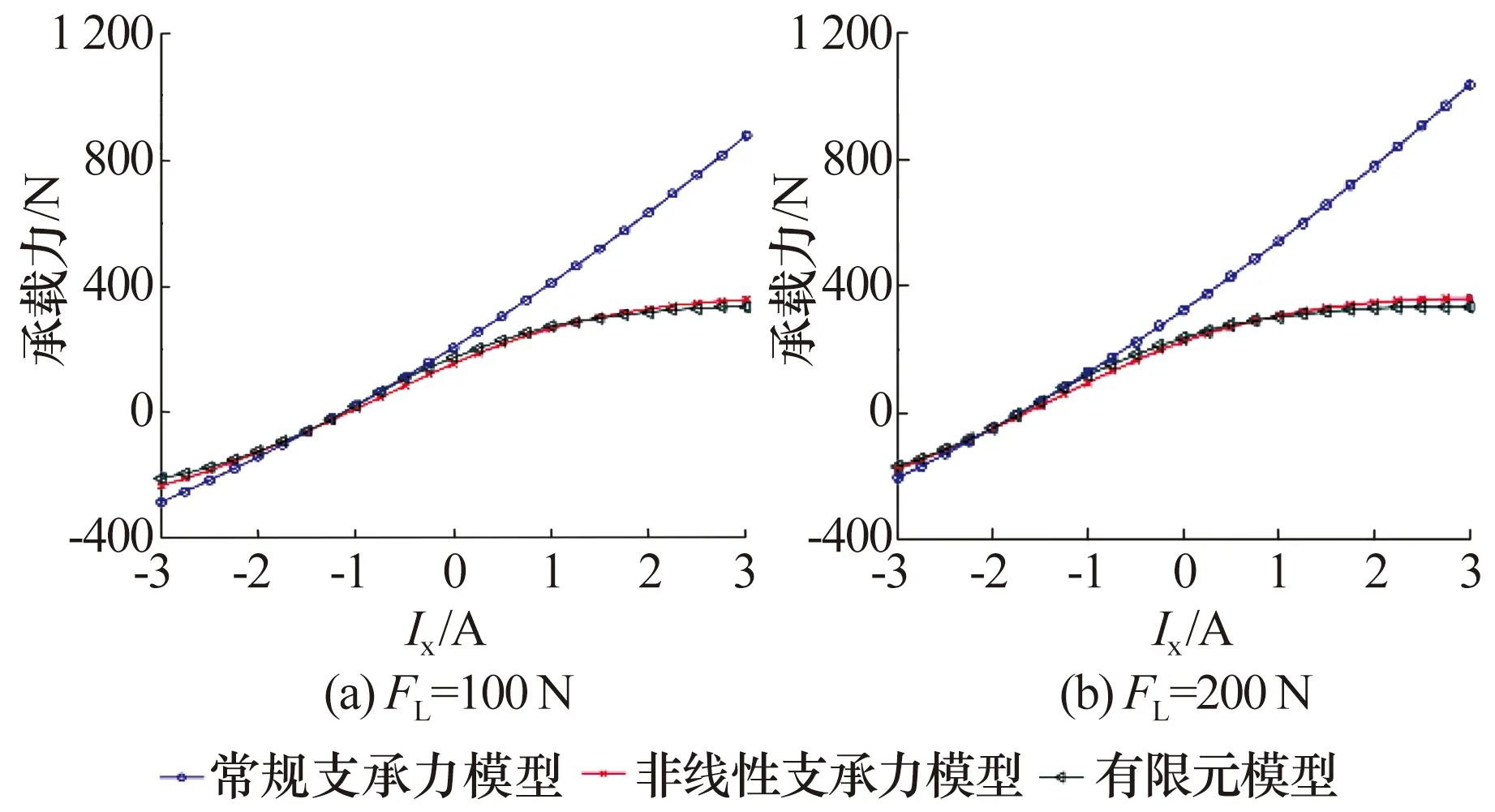
圖6 不同負載下轉子承載力曲線Fig.6 Load capacity curve of rotor under different loads
1.3 磁懸浮轉子系統動力學模型
采用Euler-Bernoulli 梁單元模擬轉軸,將轉子離散為4個軸段單元和 5個節點,如圖7所示。為考慮非線性因素對支承特性的影響,引入非線性支承力,而若將主動磁懸浮軸承單元非線性支承力作為阻尼、剛度元素處理,求解困難,在此將軸承非線性支承力當作轉子所受外激勵力,并施加在1#,5#節點上。
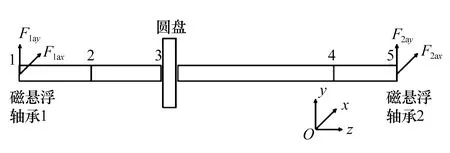
圖7 磁懸浮轉子系統有限元模型Fig.7 Finite element model of magnetic levitationrotor system
各剛性圓盤單元、彈性軸段單元的運動方程參考文獻[11],轉子的廣義位移矢量為
(2)
式中:xk,yk(k=1,2,…,5)分別為節點k在x,y方向的位移;θkx,θky分別為節點k繞x,y軸的角位移。
結合轉子各軸端與圓盤的運動方程,可得轉子在xOz,yOz平面的運動方程為
(3)
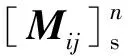
F1=(F1ax,0,0,0,udω2sin(ωt)+FL,0,0,0,F2ax,0)T,
F2=(F1ay,0,0,0,udω2cos(ωt),0,0,0,F2ay,0)T。
磁懸浮轉子系統動力學方程為
(4)
在此基礎上,采用Newmark-β法可得磁懸浮轉子系統的不平衡響應。
2 運行參數對系統不平衡響應的影響
選取控制參數:比例系數kP=40,積分系數kI=100,微分系數kD=0.05。
2.1 負載對系統不平衡響應的影響
轉子角速度ω為300 rad/s時,不同負載下磁懸浮轉子系統圓盤在y方向上的不平衡響應如圖8所示:1)常規磁懸浮單轉子系統圓盤處的響應瀑布圖僅存在轉子的基頻fi;2)在非線性磁懸浮轉子系統中,隨負載增大,系統在圓盤處的不平衡響應瀑布圖中除了轉子的基頻之外,基頻的倍頻(2fi與3fi)也被激發出來,系統非線性支承特性明顯。說明磁懸浮軸承非線性支承特性對磁懸浮轉子系統的不平衡響應有明顯影響,負載較大時,系統不平衡響應更復雜。
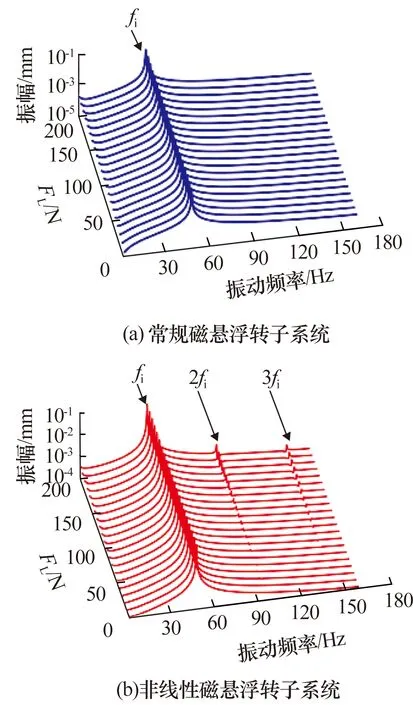
圖8 不同負載下磁懸浮轉子系統圓盤處的不平衡響應瀑布圖Fig.8 Waterfall diagram of unbalance response at disk ofmagnetic levitation rotor system under different loads
2.2 轉子角速度對系統不平衡響應的影響
負載FL為200 N時,不同轉子角速度下磁懸
浮轉子系統圓盤在y方向上的不平衡響應如圖9所示:常規與非線性磁懸浮轉子系統的不平衡響應基頻與倍頻規律同圖8,非線性磁懸浮轉子系統中倍頻信號僅在某個范圍內被激發,此時系統振幅增大,非線性支承特性加劇。說明轉子角速度也對非線性磁懸浮轉子系統的不平衡響應有影響。
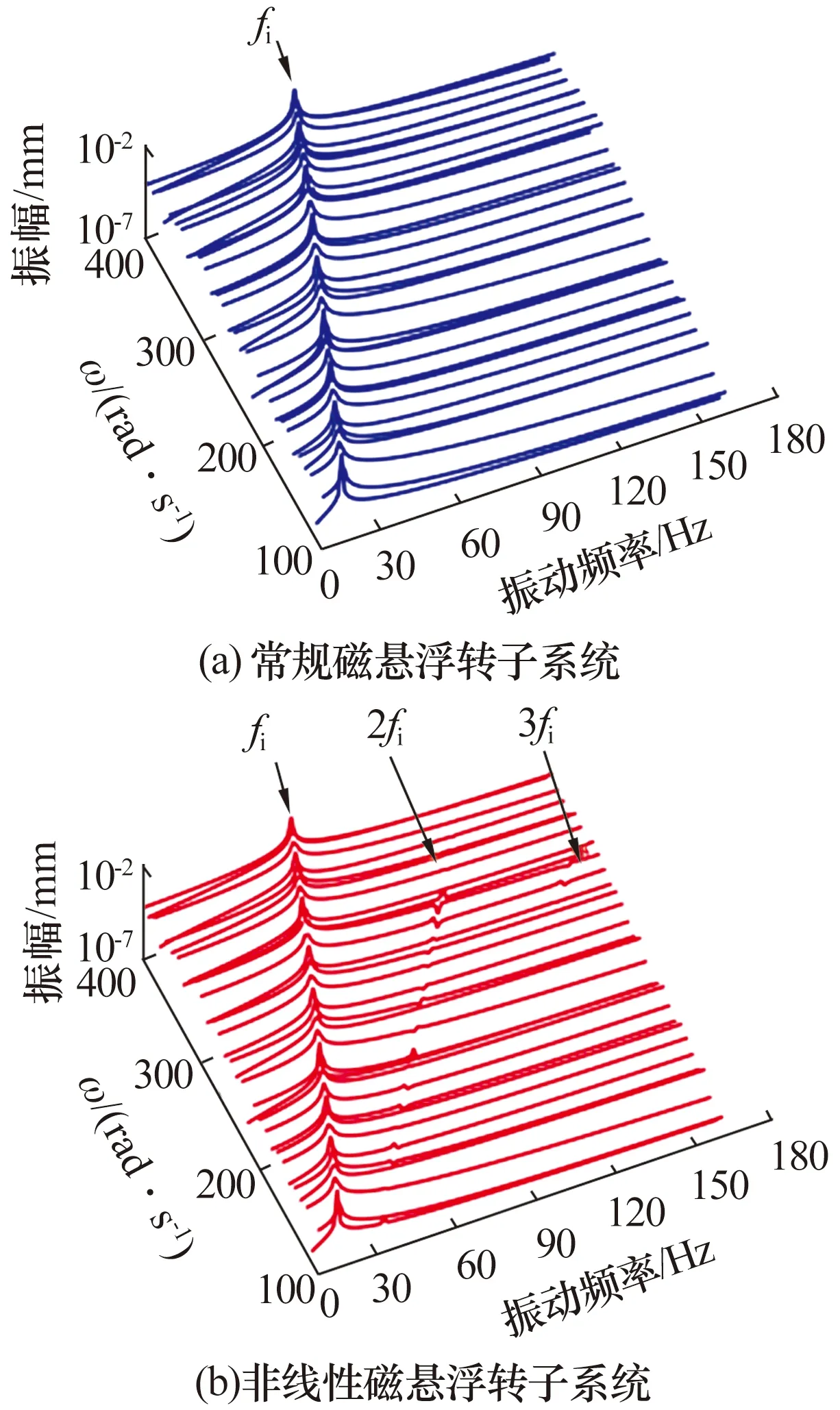
圖9 不同轉子角速度下磁懸浮轉子系統圓盤處的不平衡響應Fig.9 Unbalance response at disk of magnetic levitationrotor system under different rotor angular velocities
不同轉子角速度下磁懸浮轉子系統穩定運行區域(系統所能承受最大負載區域的面積)如圖10所示:1)常規和非線性磁懸浮轉子系統的最大承載力隨轉子角速度變化而變化,說明兩系統的穩定運行區域與轉子角速度有關;2)在相同轉子角速度范圍內,非線性磁懸浮轉子系統穩定運行區域明顯小于常規磁懸浮轉子系統,說明非線性磁懸浮轉子系統穩定性較差。
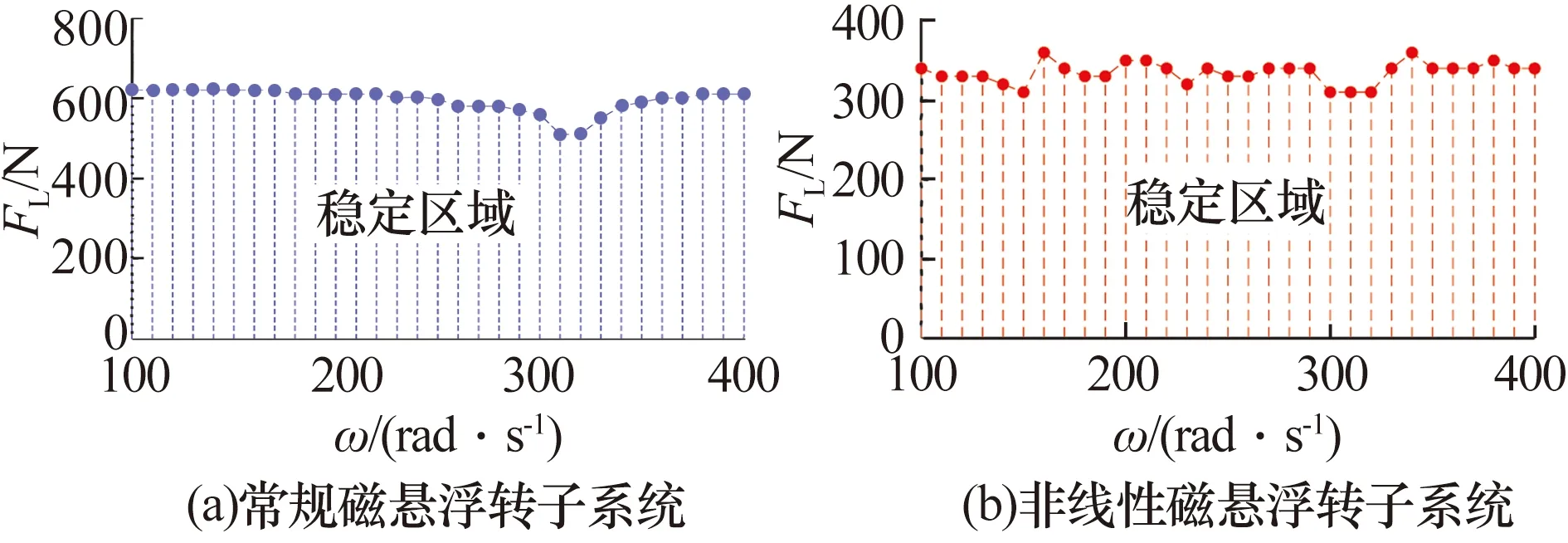
圖10 不同轉子角速度下磁懸浮轉子系統穩定運行區域Fig.10 Stable operation region of magnetic levitationrotor system under different rotor angular speeds
2.3 小結
在實際運行過程中,應盡量避免系統在較大的負載下工作,且應合理選擇系統轉速,以減小磁懸浮軸承非線性支承特性對系統的影響。
3 控制參數對系統不平衡響應的影響
選取運行參數FL=200 N,ω=300 rad/s。積分系數對系統響應的影響主要體現在低頻段,對高頻段的動態響應影響較小,此處不做分析。
3.1 比例系數對系統不平衡響應的影響
當kI為100,kD為0.05時,不同比例系數下磁懸浮轉子系統圓盤在y方向上的不平衡響應如圖11所示:1)常規磁懸浮轉子系統只存在轉子的基頻fi;2)非線性磁懸浮轉子系統響應中出現了轉子倍頻(2fi與3fi),且系統振幅隨比例系數增大而增大,當kP大于40時,轉子3倍頻(3fi)被顯著激發, 說明比例系數對非線性磁懸浮轉子系統影響顯著。應合理選擇比例系數,避免系統產生較大的振幅,從而減小磁懸浮軸承非線性支承特性對系統不平衡響應的影響。
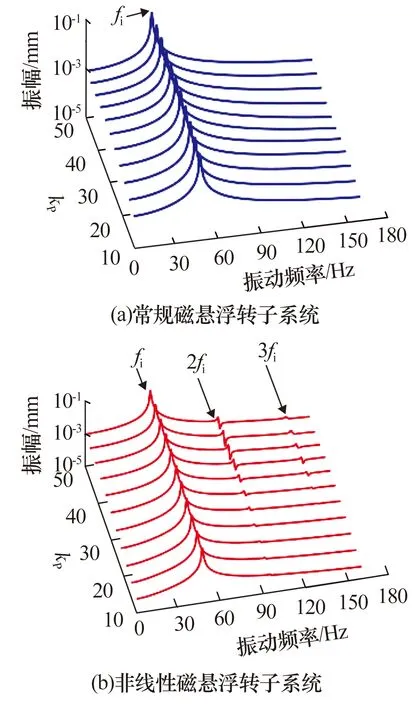
圖11 不同比例系數下磁懸浮轉子系統圓盤處的不平衡響應Fig.11 Unbalance response at disk of magnetic levitationrotor system under different proportional coefficients
不同比例系數下磁懸浮轉子系統穩定運行區域如圖12所示,非線性磁懸浮轉子系統穩定性較差。
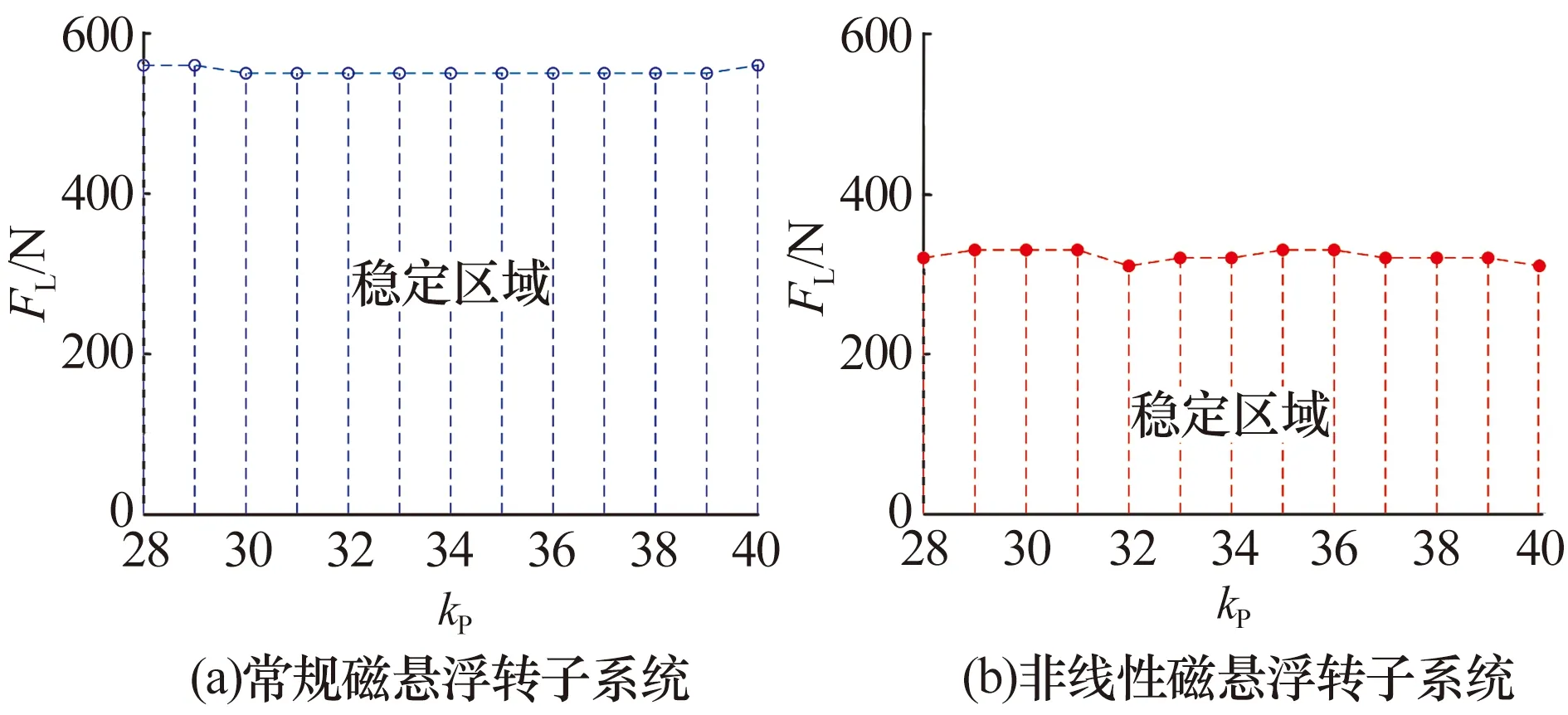
圖12 不同比例系數下磁懸浮轉子系統穩定運行區域Fig.12 Stable operation region of magnetic levitation rotorsystem under different proportional coefficients
3.2 微分系數對系統不平衡響應的影響
當kI為100,kP為40時,不同微分系數下磁懸浮轉子系統圓盤在y方向上的不平衡響應如圖13所示:1)常規磁懸浮轉子系統僅存在轉子的基頻fi;2)當微分系數較小時,非線性磁懸浮轉子系統抑制振動的能力有限,系統非線性特性明顯,在系統的響應瀑布圖中出現了轉子倍頻(2fi與3fi),隨微分系數增大,系統抑制振動的能力增強,系統非線性特性減弱,響應中2fi與3fi幅值逐漸減小,當微分系數大于0.5時,3fi接近消失。說明微分系數對非線性磁懸浮轉子系統的不平衡響應有明顯影響,較大的微分系數能有效減小磁懸浮軸承非線性支承特性對系統不平衡響應的影響。
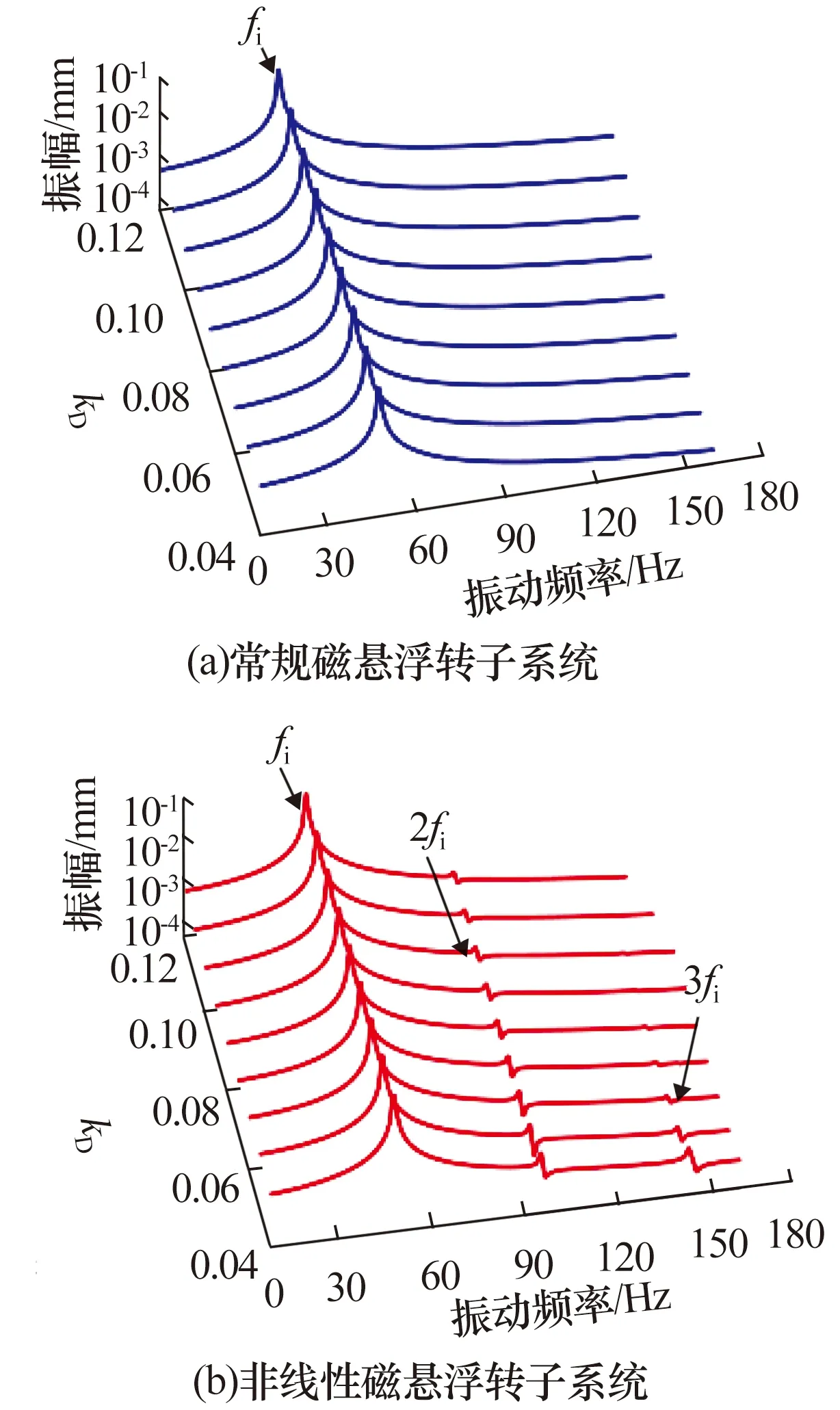
圖13 不同微分系數下磁懸浮轉子系統圓盤處的不平衡響應Fig.13 Unbalance response at disk of magnetic levitationrotor system under different differential coefficients
不同微分系數下磁懸浮轉子系統穩定運行區域如圖14所示,非線性磁懸浮轉子系統穩定性較差。
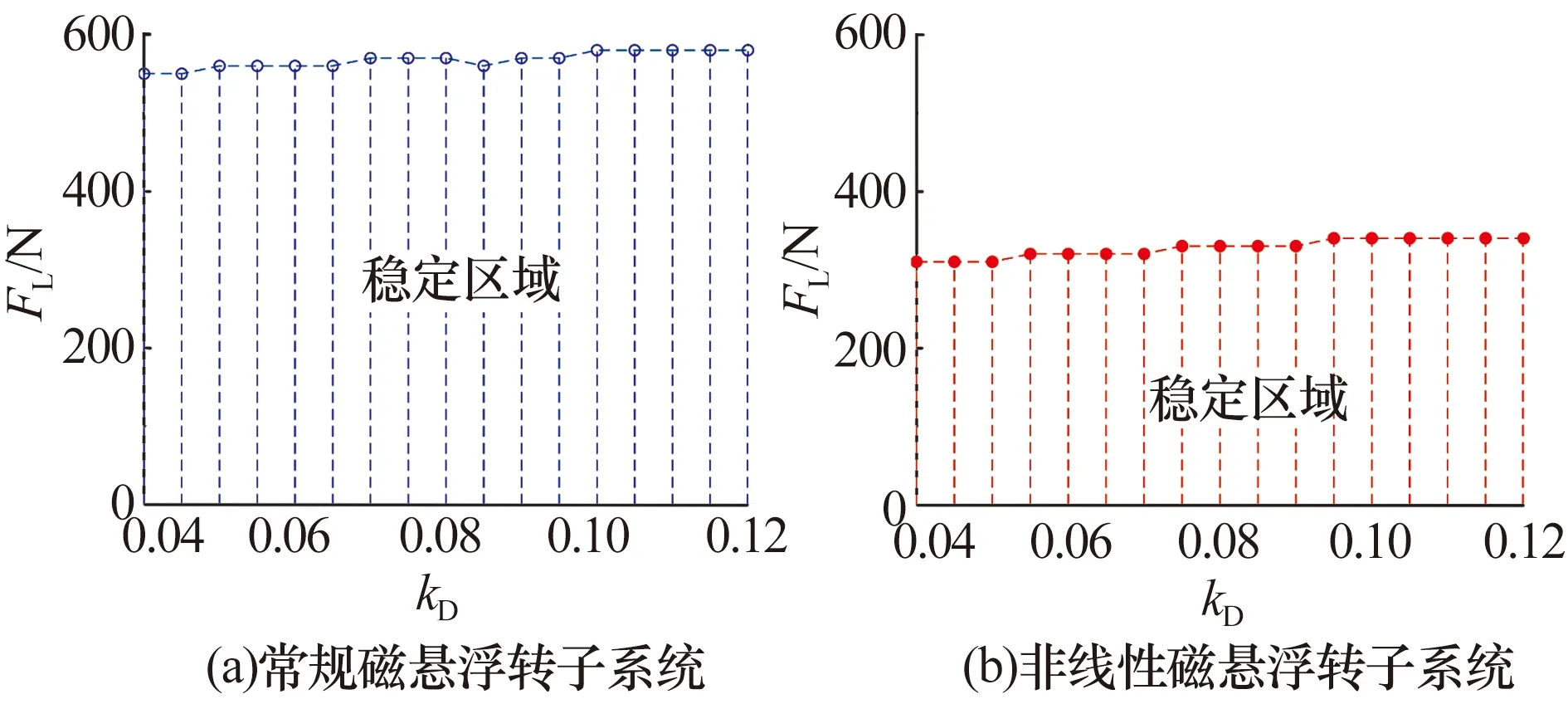
圖14 不同微分系數下磁懸浮轉子系統穩定運行區域Fig.14 Stable operation region of magnetic levitation rotorsystem under different differential coefficients
4 結論
建立非線性磁懸浮轉子系統動力學模型,分析了運行參數和控制參數對系統不平衡響應的影響,得出以下結論:
1)考慮非線性支承特性時,較大的負載會使系統的不平衡響應中出現轉子基頻的倍頻,響應復雜。
2)與常規系統相比,相同轉速范圍內考慮非線性支承特性時系統更易失穩。
3)考慮非線性支承特性時,比例系數較大和微分系數較小會使系統振幅增大,激發的轉子倍頻顯著。選取合適的比例系數與微分系數可有效減小磁懸浮軸承非線性支承特性對系統不平衡響應的影響。

