雜交粒子群算法在含模糊價值評判的旅游線路優化中的應用*
陽光學院基礎教研部 俞超群
針對粒子群算法在求解時容易早熟收斂,搜索得到最優解的能力差,引入遺傳算法中的雜交思想,采用改進后的粒子群算法,應用對福州市10個景點的旅游線路的規劃,結合不同旅游價值取向的游客,將雜交粒子群算法應用到含模糊價值評判的旅游線路的優化研究中去。通過仿真實驗,驗證了該算法理論運用于旅游線路能有效提高尋優的效率,給游客及旅行社一個比較合理的意見和建議。
隨著社會經濟的發展,近年來,周邊游逐漸成為福州人的旅游線路的首選,旅游線路的設計和優化,是各個旅行社以及游客關注的問題所在,節約時間成本,優化旅行距離,是旅行線路選擇的一個關注點。考慮到游客的旅行價值偏好[1],文獻[1]將模糊評價引入遺傳算法理論,建立基于遺傳算法的旅行線路優化算法,設計出既滿足追求最少的路程時間消耗和又滿足游客最大的旅游價值的旅行線路。但遺傳算法編碼復雜,收斂速度慢,導致尋優過程耗時較長。粒子群算法[2](PSO)是對鳥類覓食行為這樣一個簡單的社會系統進行模擬,通過迭代的形式進行全局優化的一種群體智能算法,目前已經開始應用于諸多領域[3-5],其在優化問題上的研究已經逐漸被人們重視,但是如果優化問題的搜索空間大,粒子群算法在求解時容易早熟收斂,不容易得到最優解。雜交粒子群算法[6]由Angeline提出,將遺傳算法中雜交的概念引入到粒子群算法中,是對粒子群算法的一種改進,把個體粒子的交叉、變異操作引入到粒子群的結構當中,該算法保留了粒子間的差異,同時其在收斂性和魯棒性都優于標準粒子群算法。本文采用雜交粒子群算法,結合模糊評價理論[7],建立基于雜交粒子群算法的旅游線路的優化算法,充分發揮遺傳算法和粒子群算法的優勢,以期選擇的線路既滿足實現最少的路程時間消耗,又能給予游客最大的旅游價值體驗。
1 旅游線路優化問題描述
旅游線路選擇問題是指具有一定價值偏好的游客從追求最小的路程時間消耗和滿足最大旅游價值感出發,在選定的一組景點中選擇合適的起點進行遍歷。為了便于進行比較,采集的景點坐標和價值偏好均采用文獻[1]的數據,在百度地圖上選定10個景點,采集景區坐標,針對景點的景觀屬性和游客的主觀感受構造綜合評判矩陣,得到各個景點的模糊綜合評價[1]。每個景區的坐標、對應序號以及旅游價值如表1所示。
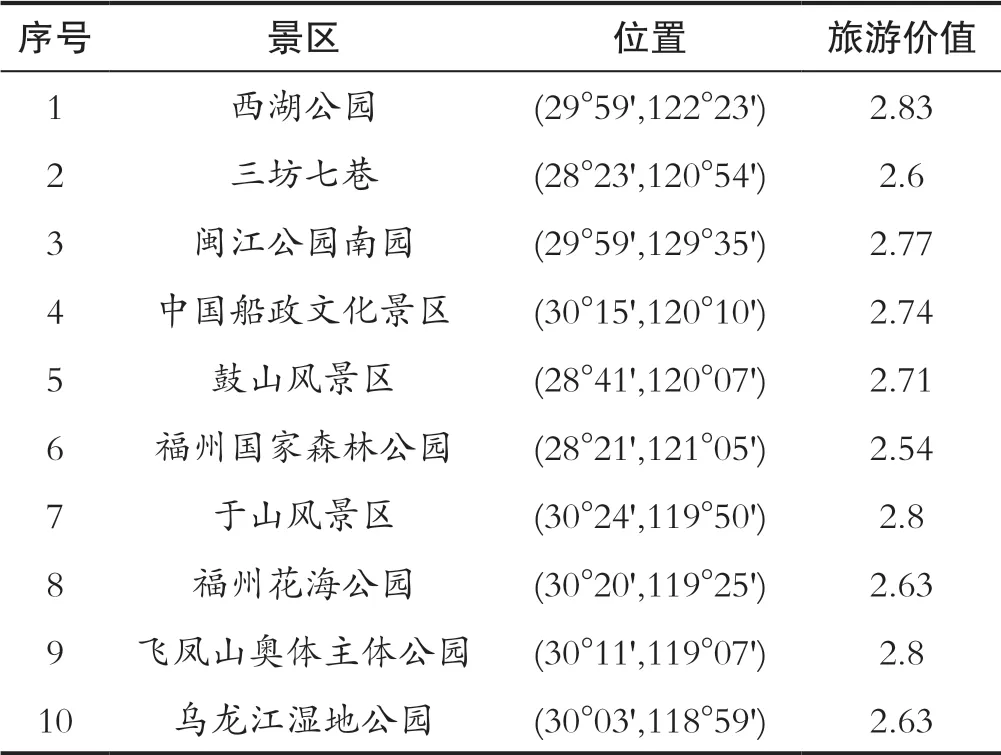
表1 10個景區位置的數字序號、位置和旅游價值Tab.1 Number, location and tourism value of 10 scenic spots
文獻[1]中單獨利用遺傳算法進行求解可以實現旅游價值的優化,但收斂速度慢,尋優過程耗時較長。
2 粒子群算法和雜交粒子群算法簡介
粒子群優化算法[2]是于1995年首次提出來的一種在全局范圍內搜索最優解的群體智能算法,根據目前廣泛使用的標準粒子群算法的流程,該算法的數學思想是:設m維空間中有popsiz個粒子,第i個粒子在時刻t的位置為
群體最優位置(全局極值)為gbestt=[g1,g2,…,gm]T,
所有的粒子都通過追尋個體極值和全局極值在這個群體空間中飛行以找到最優解。其速度和位置的更新的數學表達式如下所示:
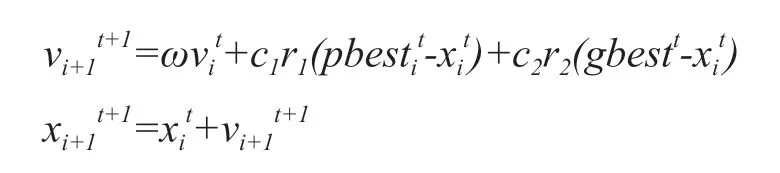
其中,ω為慣性權重系數,c1,c2為學習因子。
算法通過maxiter次迭代得到最優解,也就是將最大迭代次數作為算法的終止條件。
作為粒子群算法中最重要參數的慣性權重系數,其數值的大小決定了算法的全局和局部搜索能力的強弱,分別提出了自適應權重法、隨機權重法、線性遞減權重法。戴文智,楊新樂于2015年提出了慣性權重對數遞減的粒子群優化算法[8]。為了提高算法的收斂速度,王玉燕,李幫義,申亮將算法迭代公式中個體粒子的速度項去掉,保留位置更新公式,并將慣性權重系數放在位置矢量上,這樣算法迭代公式由二階降為一階微分方程,能有效提高算法收斂速度[9]。文獻[10]中,譚皓和王金巖等將粒子群算法和蟻群算法這兩種不同設計的雜交算子,通過模擬自然界中的物種在不同種群間的協作和交流,將雜交粒子選擇機制引入到粒子群結構中,提高算法的尋優能力,這也為粒子群算法改進給予啟發。
傳統PSO算法容易出現粒子收斂于一個非最優解后,無法跳出來導致搜索停止。為了解決這個問題,本文在進行旅游線路尋優,采取了基于雜交機制的粒子群算法[4],該算法是借鑒遺傳算法中雜交的概念,選擇一定數量的粒子放入雜交池內,將個體和最優個體或個體和群體最優的粒子進行雜交,完成粒子間的信息交換,提高尋優能力。子代位置由父代位置以一定的概率交叉得到c(x)=kp1(x)+(1-k)p2(x),其中c(x)為子代個體的位置,p1(x),p2(x)父代個體的位置,k在[0,1]上服從均勻分布,子代個體的速度

其中p1(v),p2(v)父代個體的速度。
3 雜交PSO算法對于旅行線路優化求解設計
雜交PSO算法對旅行線路優化求解設計的算法流程如圖1所示,根據圖1中雜交PSO算法對旅行線路優化求解設計的算法的流程圖所示,具體步驟如下:
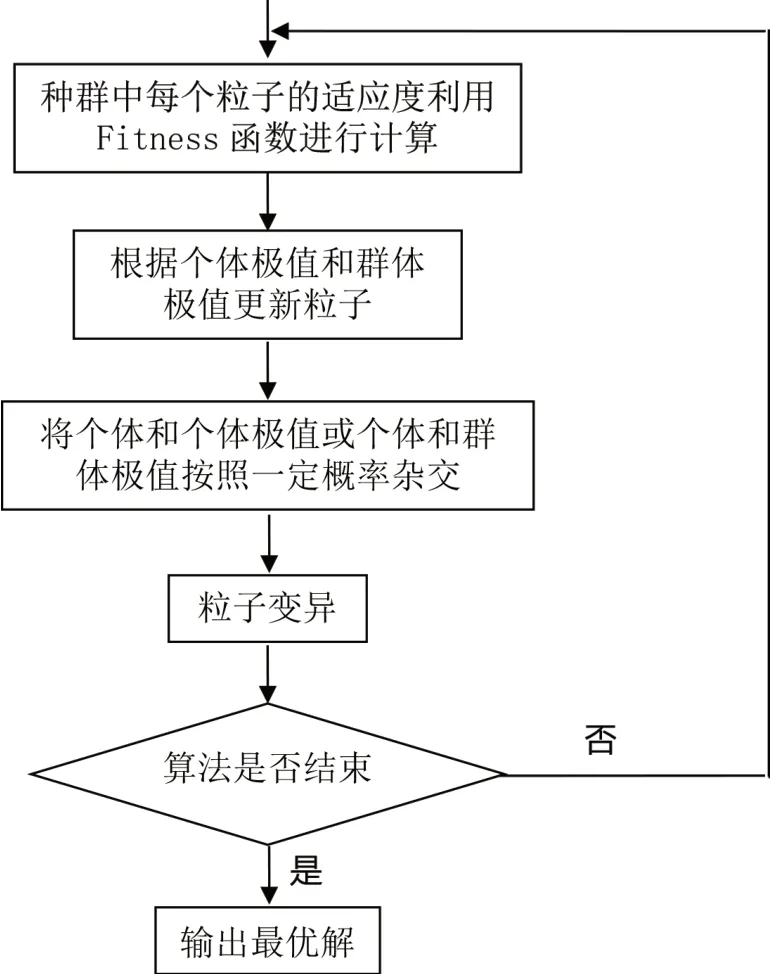
圖1 雜交PSO算法對旅行線路優化求解設計的算法流程Fig.1 The algorithm flow of the hybrid PSO algorithm for the optimal solution design of the travel route
(1)對粒子群進行初始化,設置各個粒子的位置,群體規模和迭代次數。粒子的編碼采用整數編碼的形式,每個粒子表示遍歷的10個景區的路線,比如粒子編碼為[1,2,3,4,5,6,7,8,9,10],表示從西湖公園開始,三坊七巷,閩江公園南園,船政文化景區,中國鼓山風景區,福州國家森林公園,于山風景區,福州花海公園,飛鳳山奧體主體公園這樣的一條路線。
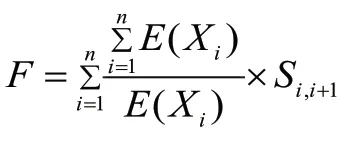
(3)將每個粒子的適應度和個體極值進行比較,更新個體極值pbesti。
(4)比較當前所有的pbesti,更新gbest。
(5)將粒子和個體極值、群體極值進行交叉,按一定的概率選擇兩個位置,然后把粒子和個體極值或者粒子和群體極值進行交叉,產生新的個體粒子,如果新的個體粒子中存在重復位置,則將個體粒子中未包括的景區序號代替重復的景區序號。
(6)對自身進行變異,隨機選擇個體粒子中的兩個位置,進行互換,如果變異后的個體粒子優于原來的粒子,才保留,否則放棄。
(7)判斷是否滿足算法終止條件,滿足則停止搜索,如果不滿足,則返回步驟(3)。
(8)輸出最終結果。
4 仿真結果
在程序中,種群規模我們取為20,總共進行100次迭代。適應度值變化情況如圖2所示,可以看出,雜交PSO算法具有較強的收斂能力,較快得到全局最優解。
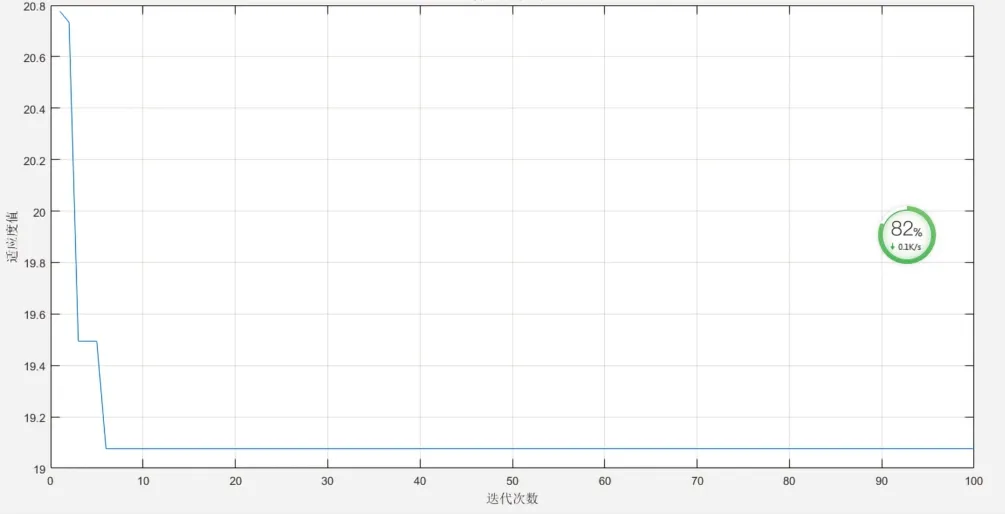
圖2 適應度值變化Fig.2 Changes in fitness value
綜合考慮游客的價值偏好和最大效率的路線規劃,如圖3所示,游客可以選擇烏龍江濕地公園—于山風景區—中國船政文化景區—福州國家森林公園—閩江公園南園—西湖公園—三坊七巷—鼓山風景區—飛鳳山奧體公園—福州花海公園。
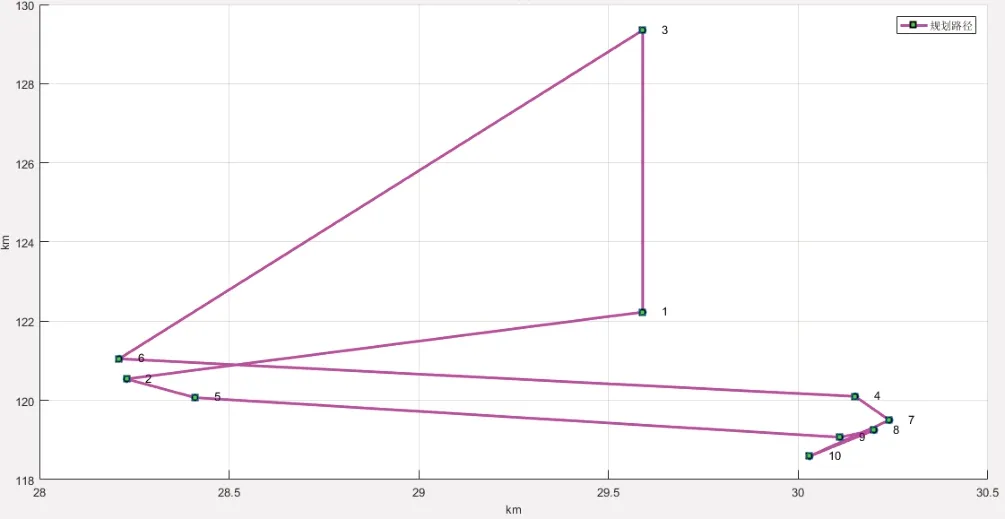
圖3 種群中10個景點的路線優化方案Fig.3 Route optimization scheme for 10 scenic spots in the population
5 結論
在旅游線路選擇問題上,既要考慮優化旅行距離和時間,使得效率最大,又要考慮游客的旅行價值偏好,在智能算法中遺傳算法編碼復雜,尋優過程耗時長,在求解最優解時,存在收斂速度慢,局部搜索能力差等缺點,本文提出了基于雜交機制的粒子群算法,并結合游客對于景點的模糊評價,設計出完善可行的旅游線路。經過實驗仿真,驗證了該算法理論運用于旅游線路能有效提高尋優的效率,給游客及旅行社一個比較合理的意見和建議。但是,對于景點的評價方式,還是比較標準化,評價手段比較單一,在應用中還要尋求更靈活的評價方式,以期能廣泛應用于旅游線路的規劃和設計。
引用
[1] 俞超群.基于模糊綜合評判和遺傳算法的旅游線路的優化[J].寧德師范學院學報(自然科學版),2018,30(2):171-175+181.
[2] 楊明軒.粒子群算法的改進及應用研究[D].岳陽:湖南理工學院,2020.
[3] 張津源.基于改進粒子群算法的物流路徑規劃研究[D].哈爾濱:哈爾濱師范大學,2021.
[4] 邢曉溪.粒子群算法研究進展[J].數據通信,2015(3):19-21+30.
[5] 趙先章,常紅星,曾雋芳,等.一種基于粒子群算法的移動機器人路徑規劃方法[J].計算機應用研究,2007(3):181-183+186.
[6] 黃煒霖,劉建軍,張明,等.帶有退火和雜交變異思想的改進粒子群算法[J].計算機工程與應用,2015,51(19):43-49.
[7] 徐永琳,王斐然.基于多因素模糊綜合評價的最優旅游線路分析[J].湖北民族學院學報(自然科學版),2014(1):81-84.
[8] 戴文智,楊新樂.基于慣性權重對數遞減的粒子群優化算法[J].計算機工程與應用,2015,51(17):14-19+52.
[9] 王玉燕,李幫義,申亮.TPT-CLSC的協調研究[J].中國管理科學,2007(05):101-106.
[10] 譚皓,王金巖,何亦征,等.一種基于子群雜交機制的粒子群算法求解旅行商問題[J].系統工程,2005(04):83-87.

