超精密微小型車銑復合加工機床的空間誤差建模與靈敏度分析＊

鄭中鵬 金鑫 郭嘉靖 高瑞麟 井浩 李二波

（①清華大學機械工程系，北京 100084；②北京理工大學機械與車輛學院，北京 100081）

隨著尖端科技和國防工業的不斷發展，微小型復雜結構件的加工精度要求越來越高。但是，機床在實際加工運動過程中與理想運動存在偏離狀態，導致刀具運動軌跡偏離設定的目標位置，進而產生加工幾何誤差，降低了工件的加工精度[1]。因此，開展加工誤差建模與補償是必不可少的。

誤差建模是機床的各項誤差參數與工件精度之間的數學關系，屬于誤差補償核心的部分。Schultschik R 在1977 年首次提出了機床空間誤差概念，并且采用閉合矢量鏈方法表達精密三軸坐標鏜床的誤差，為日后的學者研究加工誤差奠定了基礎[2]。天津大學的劉又午等人開展了多體系統動力學理論研究，提出了一種基于多體系統理論（MBS）的機床運動幾何誤差模型[3]。張宏韜等人提出一種定量表達機床各軸在運動過程的位置誤差模型，進一步給出分步解耦補償方法和機床的誤差補償數學模型[4]。同時，針對加工過程熱引起的機床熱變形降低加工精度的問題，Chen J S 等人以高精密機床靜壓主軸為研究對象，研究影響主軸精度的熱因素，通過有限元分析，計算主軸相關熱量參數[5]。上海交通大學項四通等人基于螺旋理論提出了五軸機床的空間誤差建模和補償策略，建立空間誤差統一模型，并在多臺試驗機床上進行了驗證[6]。北京工業大學范晉偉等人開展了復合數控機床幾何誤差建模與靈敏度分析，識別了影響機床加工精度的關鍵性幾何誤差[7]。

超精密車銑復合加工機床與傳統的加工機床相比，車銑復合加工機床一般有2 個旋轉軸，3～5 個直線軸，甚至更多直線軸。更多的旋轉軸和直線軸的組合意味著機床存在更復雜的誤差補償模型關系。因此，為了進一步提高超精密車銑復合加工復雜微小型構建的精度，指導和優化機床結構設計，本文以北京理工大學自主開發的超精密車銑復合加工機床CXKG25-I 為研究對象，基于多體系統理論，建立超精密車銑復合加工機床空間幾何誤差模型，并對機床進行誤差靈敏度分析，獲得影響加工精度的關鍵誤差因素。

1 超精密車銑復合加工機床結構分析

針對三維復雜微小型結構件的高精度加工需求和車銑復合功能特點，北京理工大學微小型制造研究所自主開發了超精密車銑復合加工機床CXKG25-I[8]，其結構、實物分別如圖1、圖2 所示。該機床包括X、Y、Z這3 個微米級精度宏動軸，U、W兩個亞微米級精度直線軸，旋轉B軸和旋轉C軸，可實現七軸五軸聯動復雜結構件加工。此外，為了實現加工零件的在位實時補償功能，機床上安裝有在位測量系統，可實時檢測零件尺寸。

圖1 超精密車銑復合加工機床CXKG25-I 結構

圖2 超精密車銑復合加工機床CXKG25-1 樣機

目前，廣泛使用多體系統理論開展空間幾何誤差建模，這種方法通用性強，是一種比較成熟的建模體系。該理論將機床部件抽象為機床誤差信息的剛體，每個剛體對應一個部件系統，可以建立超精密車銑復合加工機床的各個拓撲結構，并采用矩陣反映各個系統之間的聯系，機床各個部件元素通過機床尺寸鏈反映刀尖軌跡[9]。如圖3 所示，超精密車銑復合加工機床CXKG25-I 的尺寸鏈可以分為工件鏈、刀具鏈和運動鏈，具體傳遞鏈可表示為：

圖3 超精密車銑復合加工機床運動鏈

（1）床身到工件：“床身0→直線導軌X軸1→直線導軌Y軸2→旋轉C軸3→工件W軸4”。

（2）床身（基座）到刀具：“床身0→直線導軌Z軸5→直線導軌B軸6→直線導軌U軸7→直線導軌W軸8→刀具9”。

2 超精密車銑復合機床空間幾何誤差元素分析

根據ISO 230-1 和ISO 230-7 的定義，機床的幾何誤差主要取決于位置相關的幾何誤差（PDGEs）和位置無關的幾何誤差（PIGEs）[10]。其中，位置相關的幾何誤差（PDGEs）指的是各個直線軸、旋轉軸自身存在的位置誤差；位置無關的幾何誤差（PIGEs）主要指的是各個軸間的垂直度誤差。此外，由于機床每個運動軸均可以視作剛體，具有6個自由度，所以存在6 項基本幾何誤差，包括3 個線性幾何誤差和3 個旋轉角度誤差；對于平動軸，線性幾何誤差根據移動方向可以分為定位誤差和直線度誤差，角度誤差根據繞不同軸旋轉方式，可以分為俯仰誤差、偏擺誤差和滾擺誤差[11]。

如圖4 所示，以超精密車銑復合機床Z軸幾何誤差分析為例，Z軸包括3 項線性平動誤差，分別是Z方向的定位誤差δz(z)，X方向的直線度誤差δx(z)和Y方向的直線度誤差 δy(z)。3 項角度誤差分別是繞X軸旋轉的俯仰誤差εx(z)，繞Y軸旋轉的偏擺誤差εy(z)和繞Z軸旋轉的滾擺誤差 εz(z)。由于超精密車銑復合機床CXKG25-I 為七軸五聯動復合加工機床，有5 個直線軸，共30 項位置相關的幾何誤差（PDGEs）。

圖4 超精密車銑復合加工機床Z 軸幾何誤差元素

如圖5 所示，對于旋轉軸而言，同樣存在6 項誤差幾何項目，包括3 項線性誤差和3 項角度誤差。根據靜壓主軸的形狀和坐標關系，具體的誤差項目分別為C軸軸向定位線性誤差 δz(c)，X軸方向的徑向線性誤差 δx(c)，Y軸方向的徑向線性誤差 δy(c)，繞Z軸方向旋轉的C軸定位角度誤差 εz(c)，繞X軸方向傾斜的角度誤差 εx(c)和繞Y軸方向傾斜的角度誤差 εy(c)。需要指出的是，超精密車銑復合加工機床共有B軸和C軸2 個旋轉軸，因此共有12 項位置相關幾何誤差(PDGEs)。

圖5 超精密車銑復合加工機床的C 軸幾何誤差元素

圖6 是超精密車銑復合加工機床的垂直度誤差元素示意圖，其中5 個直線軸兩兩之間存在8 項垂直度誤差，分別是 γxy、γyz、γxz、γuy、γuw、γuz、γwx、γwy；直線軸與旋轉軸之間存在7 項垂直度誤差，分別是γxb、γzb、γub、γwb、γcx、γcy、γcu，因此共有15 項垂直度誤差(PIGEs)。

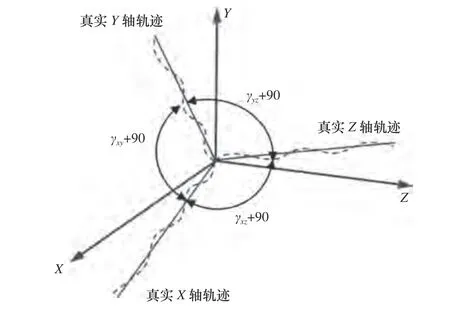
圖6 超精密車銑復合加工機床的垂直度誤差元素分量

綜上，超精密車銑復合加工機床CXKG25-I 所有的空間幾何誤差因素如表1 所示。

表1 超精密加工機床的幾何誤差元素

3 超精密車銑復合機床空間誤差建模

在多體運動學理論中，任意兩個相鄰的剛體之間的誤差包括位置矩陣、位置誤差矩陣、運動矩陣和運動誤差矩陣[12]。此外，如果不考慮位置誤差和運動誤差的話，任意兩個相鄰剛體之間的關系可以表示為，剛體i與相鄰的剛體j之間的轉換矩陣具體表示如下。

根據表達式（1）,工件尺寸鏈的傳遞矩陣如下。

根據表達式（1），刀具尺寸傳遞鏈的矩陣如下

此外，如果沒有機械加工誤差，則理想刀尖軌跡模型如下。

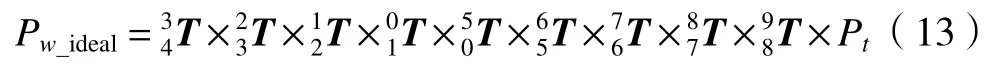
因此，機床加工誤差模型可以表示刀尖真實軌跡模型減去理論刀尖軌跡模型

4 誤差靈敏度分析

機床加工誤差補償可以在一定程度上提高車銑復合加工零件的幾何精度。但是，由于影響機床加工精度的誤差因素有57 項，對其所有的誤差辨識和補償相當復雜，因此需要建立靈敏度誤差分析模型，確定影響超精密車銑復合加工過程中的關鍵誤差因素。目前，一階靈敏度函數方法是工程計算中使用比較多的一種誤差靈敏度分析方法[13]，求出對各個方向的偏導數，得到數控機床傳動機構各個誤差的靈敏度，計算表達式如下

為了可視化分析與對比，將靈敏度數值歸一化，并計算并得到所有誤差的靈敏度系數。需要指出的是，誤差靈敏度系數在X軸、Y軸和Z軸3 個方向的各個誤差分量之和等于1，具體表達式如下

此外，在超精密車銑復合加工機床中，常常采用正交切削加工。因此，本研究中以主軸和銑削主軸垂直布局來設置初始位置參數，具體參數如表2和表3 所示。

表2 超精密車銑復合加工機床的初始位置

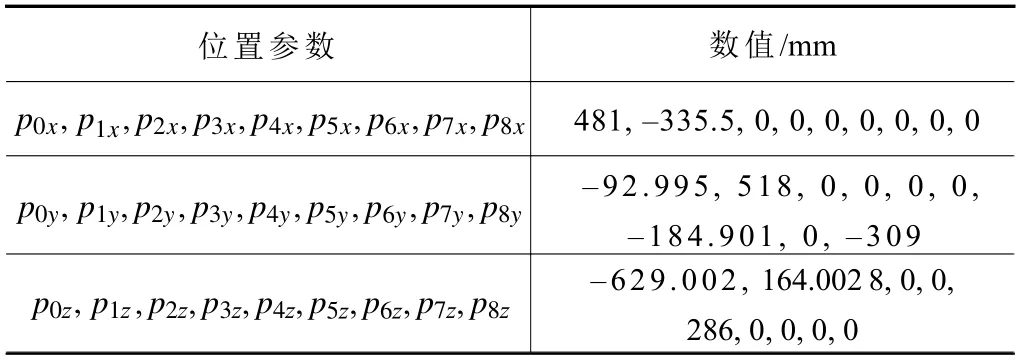
表3 超精密車銑復合加工機床各種間初始參考位置

由圖7 可知，正交車銑過程中影響X方向加工誤差(Ex)的關鍵誤差主要包括X軸繞Y軸的偏擺誤差 εy(x)，Y軸自身的滾擺誤差 εy(y)，Z軸自身的滾擺誤差 εz(z)，C軸繞Y軸的偏擺誤差 εy(c)，B軸繞Z軸的偏擺誤差 εz(b)，以及XZ、XB、CX和CU軸間的垂直度誤差,這些關鍵誤差的敏感度系數之和為76.91%,每個誤差源的靈敏度系數均在7%以上。

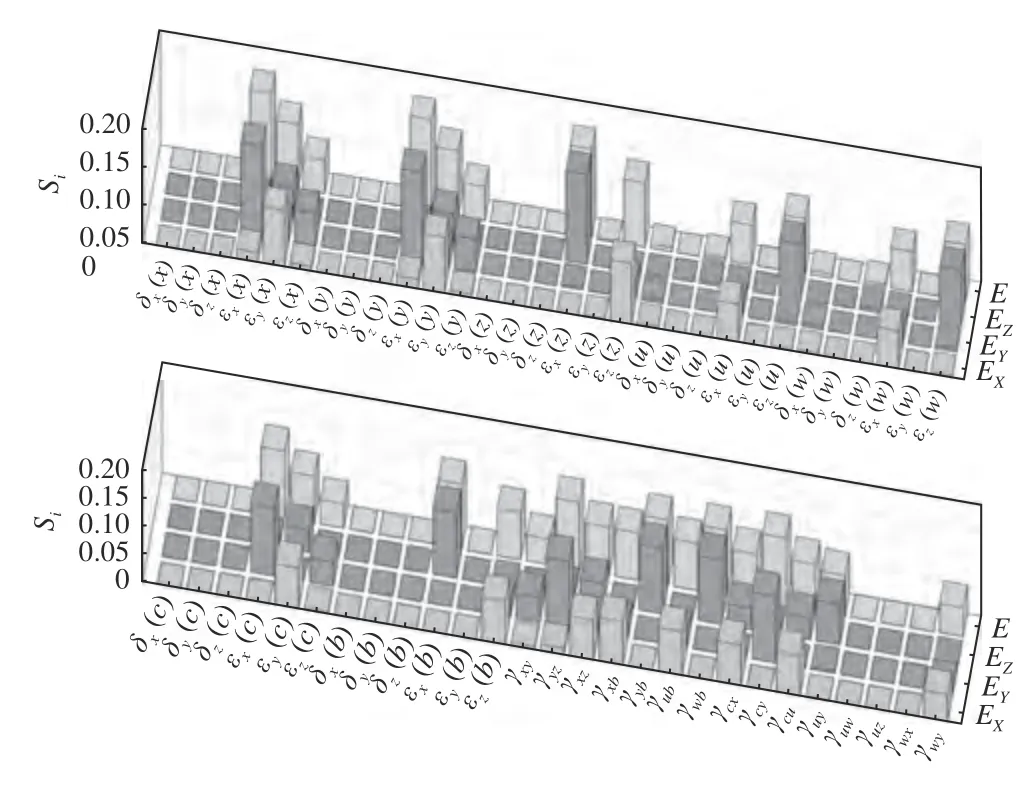
圖7 空間幾何誤差在各個誤差方向的靈敏度系數(Sx=10 mm，Sz=10 mm)

正交車銑過程中影響Y方向加工誤差(Ey)的關鍵誤差主要包括X軸繞自身的滾轉誤差 εx(x)，Y軸繞X軸的俯仰誤差εx(y),C軸繞X軸的俯仰誤差 εx(c)，以及YZ、CY軸之間的垂直度誤差。這些關鍵誤差的靈敏度系數均在12% 以上，其敏感度系數之和為60%。

最后，影響正交車銑過程中影響Z方向加工誤差(Ez)關鍵誤差主要包括Z軸繞X軸的俯仰誤差εx(z)和B軸繞X軸的俯仰誤差 εx(b)，這兩個關鍵誤差源的靈敏度系數超過12%。此外X軸繞Y軸的俯仰誤差 εy(x)，Y軸繞自身的滾擺誤差，W軸繞Z軸的滾擺誤差 εz(w)，C軸繞Z軸的滾擺誤差εz(c)，C軸繞Y軸的偏擺誤差 εy(c)等誤差項也對結果具有一定的影響。需要注意的是，相比平動誤差而言，綜合誤差受到角度旋轉誤差分量和各軸間的垂直度誤差分量的影響更大，因此在后續加工誤差補償過程中優先考慮角度旋轉誤差和垂直度誤差的影響。

此外，加工過程中，各個運動軸的位置和姿態不斷改變，零件和刀具的位置也隨之不斷變化，綜合誤差模型的關鍵靈敏度系數也在不斷變化，為了進一步揭示獲得的關鍵誤差分量對加工精度的影響，以常用低剛度結構件（撓性接頭 200 mm×200 mm以內）加工的范圍內進行靈敏度分析。圖8、圖9分別是固定X軸、移動Z軸（200 mm），固定Z軸、移動X軸（200 mm）的靈敏度分析，與圖7 相比較，角度旋轉誤差和垂直度誤差仍然是影響綜合誤差的重要因素。但是，需要注意的是部分誤差項目隨著初始位置不同發生了變化，比如Z軸繞X軸俯仰誤差 εx(z) 隨著Z軸的移動（Sz=200 mm）而變化，這主要歸因于行程增加使Z軸部件的制造誤差、裝配誤差和伺服控制誤差增加導致的。

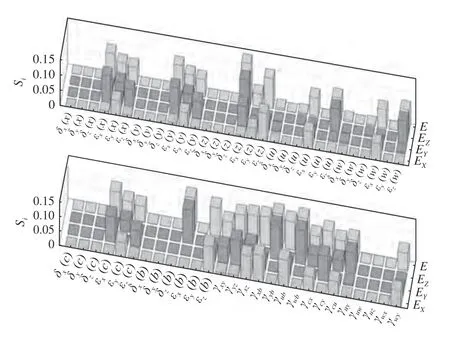
圖8 空間幾何誤差在各個誤差方向的靈敏度系數(Sx=10 mm,Sz=200 mm)

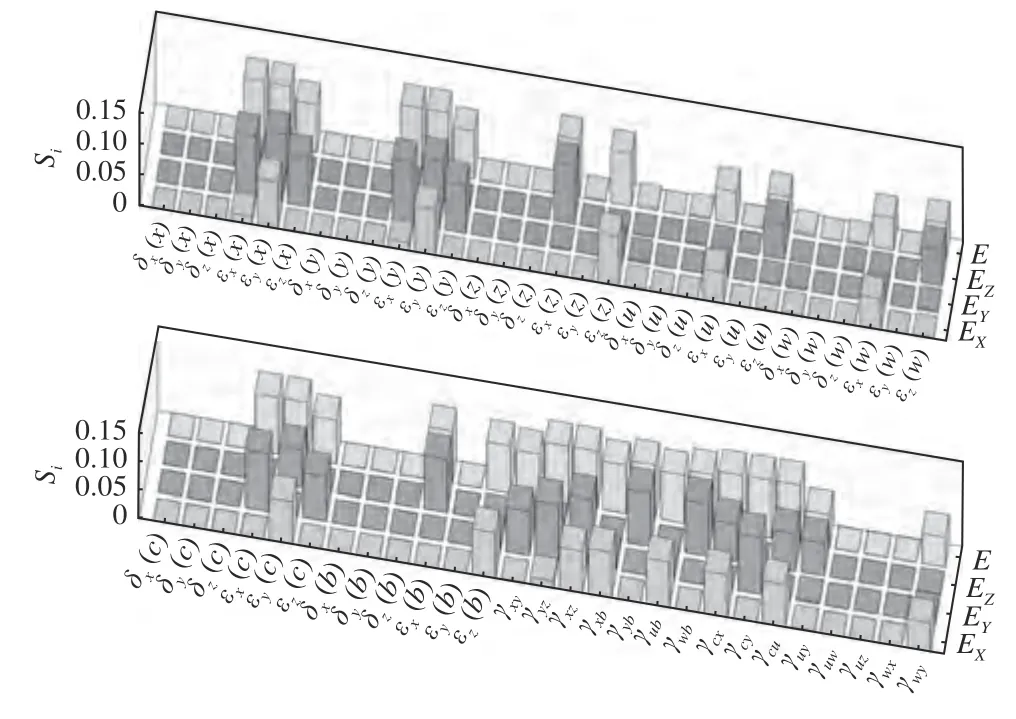
圖9 空間幾何誤差在各個誤差方向的靈敏度系數(Sx=200 mm,Sz=10 mm)

5 結語

（1）分析了超精密車銑復合加工機床CXKG25-I的57 項幾何誤差元素，其中包括42 項運動誤差和15 項垂直度誤差，建立了超精密車銑復合加工機床的空間幾何誤差補償模型。

（2）獲得了影響加工誤差因素的關鍵幾何敏感誤差因素。研究表明：相比較平動線性誤差而言，機床加工精度受到角度旋轉誤差分量和垂直度誤差分量的影響更大。