基于LMD 能量熵和支持向量機(jī)的齒輪箱故障診斷＊

徐樂(lè) 朱玉斌 郎超男

（①江蘇師范大學(xué)，江蘇 徐州 221116；②中國(guó)礦業(yè)大學(xué)，江蘇 徐州 221116）

齒輪箱是旋轉(zhuǎn)設(shè)備中常用的零部件，由于其具有傳動(dòng)比大、承載力強(qiáng)以及結(jié)構(gòu)緊密等優(yōu)點(diǎn)，被廣泛應(yīng)用到航空航天、重型機(jī)械等各類旋轉(zhuǎn)機(jī)械設(shè)備中。但是由于旋轉(zhuǎn)設(shè)備長(zhǎng)期處于工作狀態(tài)，其齒輪箱也一直在高強(qiáng)度連續(xù)運(yùn)轉(zhuǎn)，且運(yùn)行條件較為惡劣，所以旋轉(zhuǎn)機(jī)械設(shè)備內(nèi)的齒輪箱出現(xiàn)故障概率也較大，而其一旦出現(xiàn)故障，將會(huì)導(dǎo)致整個(gè)設(shè)備無(wú)法運(yùn)行，甚者會(huì)引發(fā)事故，造成人員傷亡。因此，對(duì)旋轉(zhuǎn)機(jī)械齒輪箱工作運(yùn)行狀態(tài)進(jìn)行監(jiān)測(cè)，并對(duì)其故障進(jìn)行診斷具有重要意義。齒輪箱在出現(xiàn)故障后，其運(yùn)行引起的振動(dòng)信號(hào)是非平穩(wěn)、非線性的，需要使用有效的方法提取其故障特征，常見(jiàn)的故障特征提取方法有時(shí)域分析[1]、小波變換[2-3]和經(jīng)驗(yàn)?zāi)B(tài)分解[4-5]等。但是，時(shí)域分析缺少頻域分析，不適用于非線性信號(hào)分析；小波變換因小波基選取困難，難以得到相對(duì)理想的故障特征；經(jīng)驗(yàn)?zāi)B(tài)分解方法在分析處理中迭代循環(huán)次數(shù)較多，而且其端點(diǎn)效應(yīng)明顯，對(duì)非線性振動(dòng)信號(hào)處理的自適應(yīng)還有一定差距。

基于局部均值分解（local mean decomposition，LMD）[6]的信號(hào)分析方法是現(xiàn)階段熱點(diǎn)研究?jī)?nèi)容，它能夠?qū)⒎蔷€性信號(hào)自適應(yīng)分解成有限個(gè)不同頻率的PF 分量和殘余量，迭代次數(shù)較少并有效抑制端點(diǎn)效應(yīng)，同時(shí)解決了欠包絡(luò)、過(guò)包絡(luò)等問(wèn)題。劉洋等人[7]提出了基于LMD-SVD 和極限學(xué)習(xí)機(jī)的故障診斷方法，實(shí)現(xiàn)了風(fēng)機(jī)軸承在變工況條件下的自適應(yīng)診斷；楊靜宗等人[8]提出了基于LMD 和灰色關(guān)聯(lián)度的故障診斷方法，實(shí)現(xiàn)了小樣本條件下單向閥故障信號(hào)診斷，并驗(yàn)證了LMD 效果優(yōu)于EMD；張寧等人[9]利用LMD、樣本熵和ELM 方法結(jié)合，實(shí)現(xiàn)了行星齒輪箱故障診斷，并證明了診斷效果優(yōu)于其他方法。齒輪箱出現(xiàn)故障時(shí)，其振動(dòng)引起的能量會(huì)根據(jù)故障頻率劃分，為了實(shí)現(xiàn)非單一、多種故障齒輪箱故障特征提取，將熵理論引入[10-12]，提出LMD 能量熵概念，根據(jù)齒輪箱振動(dòng)信號(hào)在不同頻域范圍內(nèi)能量值變化提取出齒輪箱故障特征。

在機(jī)械故障識(shí)別分類中，分類效果較好的神經(jīng)網(wǎng)絡(luò)方法對(duì)訓(xùn)練和測(cè)試樣本的數(shù)量要求較大，在實(shí)際條件下，獲取大量數(shù)據(jù)樣本十分困難，獲取多種故障樣本更是不易。支持向量機(jī)（support vector machines,SVM）[13-14]非常適用于小樣本數(shù)據(jù)的分析和處理，克服了大量訓(xùn)練、測(cè)試樣本需求及經(jīng)驗(yàn)知識(shí)需求，故障分類的準(zhǔn)確性、精準(zhǔn)度更高。因此，針對(duì)實(shí)際生產(chǎn)中樣本少的情況，本文將利用SVM多故障分類器對(duì)提取的齒輪箱LMD 能量熵特征進(jìn)行訓(xùn)練和測(cè)試，實(shí)現(xiàn)對(duì)齒輪箱故障類型分類和識(shí)別。

1 算法原理

1.1 LMD 算法

LMD 方法對(duì)于任一非線性多分量振動(dòng)信號(hào)x(t)的分解步驟如下[9-15]。

（1）找出x(t)所有極值點(diǎn)ni，并求出鄰近極值點(diǎn)的均值mi與它們的包絡(luò)估計(jì)值ai。

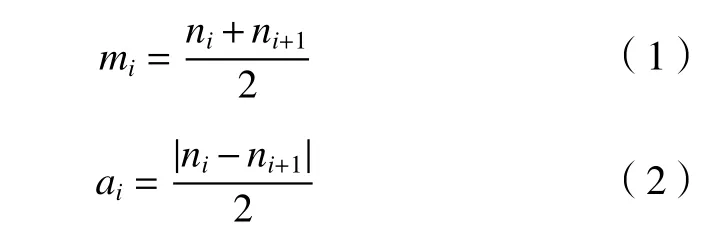
利用滑動(dòng)平均法分別對(duì)mi和ai處理，得到局部均值函數(shù)m11(t)和包絡(luò)估計(jì)函數(shù)a11(t) 。

（2）將m11(t)從信號(hào)x(t)中分離。

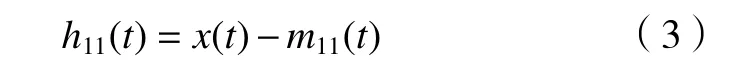
（3）對(duì)h11(t)解調(diào)，得到調(diào)頻信號(hào)s11(t)。

若s11(t)不是純調(diào)頻信號(hào)，那么將s11(t)視作原始信號(hào)重新上述步驟，直至得出純調(diào)頻信號(hào)s1n(t)，即s1n(t)對(duì)應(yīng)的包絡(luò)估計(jì)函數(shù)a1(n+1)(t)=1。

具體步驟為

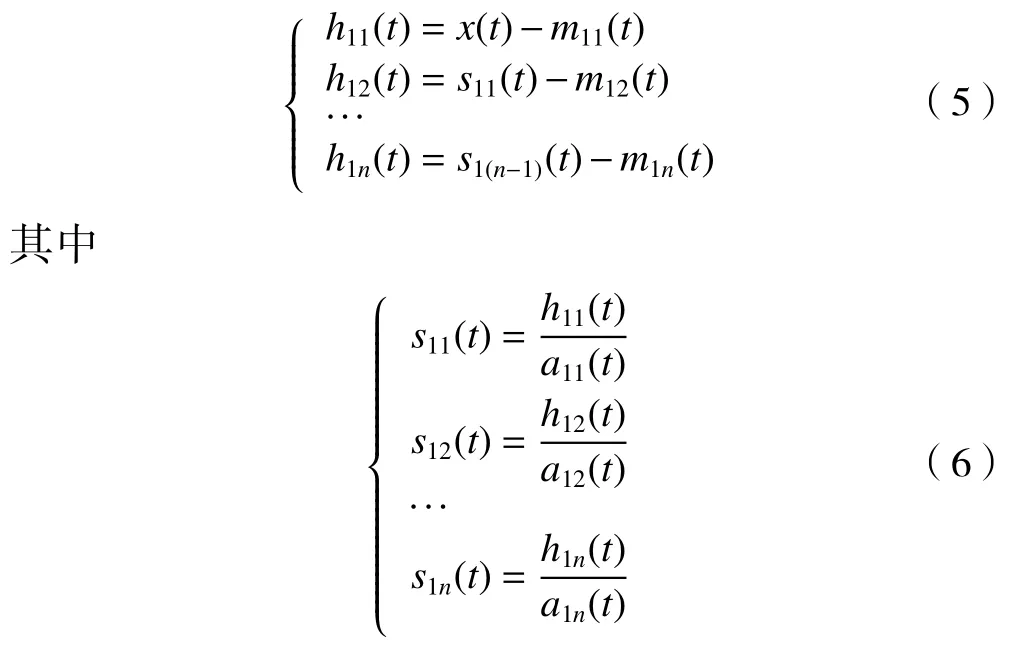
迭代終止條件為

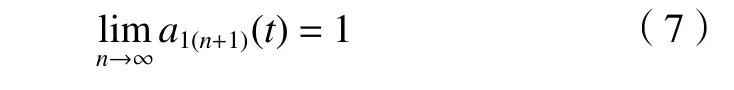
（4）求取包絡(luò)信號(hào)a1(t)。

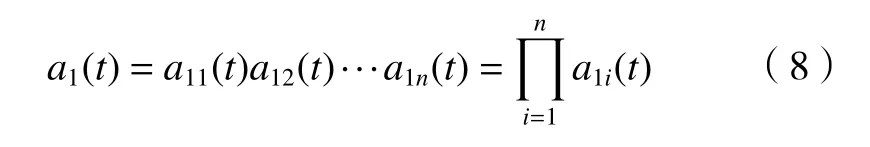
（5）將a1(t)與s1n(t)相乘，得到首個(gè)PF分量。

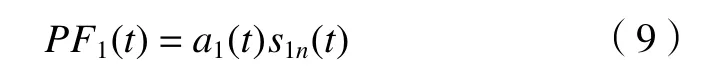
（6）在x(t)中將PF1(t)分離出去，剩余信號(hào)標(biāo)記為u1(t)。把u1(t)當(dāng)作新的信號(hào)重復(fù)上述分解步驟，循環(huán)k次，直到uk(t)為單調(diào)函數(shù)為止。

至此，x(t)被分解為k個(gè)PF分量和殘余量uk(t)。

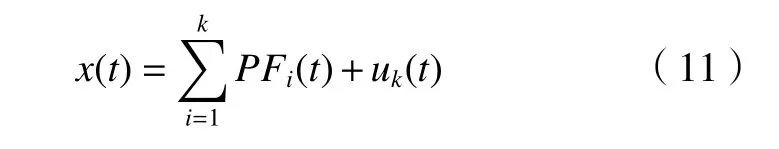
1.2 LMD 能量熵

旋轉(zhuǎn)設(shè)備運(yùn)行狀態(tài)下，其內(nèi)部的齒輪箱在無(wú)故障和發(fā)生故障兩種狀態(tài)下，振動(dòng)所包含的頻率分布不同，而且當(dāng)齒輪箱出現(xiàn)不同故障時(shí)，其頻率分布對(duì)應(yīng)的能量分布也會(huì)跟隨變化。為了分析出齒輪箱振動(dòng)信號(hào)能量分布隨其振動(dòng)頻率成分改變情況，定量地體現(xiàn)出不同故障能量分布紊亂程度，將熵理論引到LMD 分解中，提出LMD 能量熵方法。該方法的計(jì)算原理及求取公式如下。

多分量振動(dòng)信號(hào)x(t) 被LMD 分解后得到k個(gè)PF分量和殘余量uk(t)，分別求出k個(gè)PF分量對(duì)應(yīng)的能量，分別記為E1,E2,···,Ek。理論上，uk(t)為單調(diào)函數(shù)，所以其對(duì)應(yīng)的能量接近零，因此在不計(jì)算uk(t)能量情況下，x(t)本身對(duì)應(yīng)的能量與k個(gè)PF分量對(duì)應(yīng)的能量之和相等。由于得到的PF分量分別包含各自頻域范圍內(nèi)振動(dòng)信號(hào)，因此E={E1,E2,···,Ek}就構(gòu)成了能量特征在頻率域內(nèi)的自適應(yīng)分布。因此，將LMD 能量熵求取方式定義為

其中，Ei表示第i個(gè)PF分量的能量值。

2 基于LMD 能量熵和SVM 的齒輪箱故障診斷方法

基于LMD 能量熵分析，結(jié)合SVM 方法對(duì)齒輪箱故障特征提取和分類，具體步驟如圖1 所示。

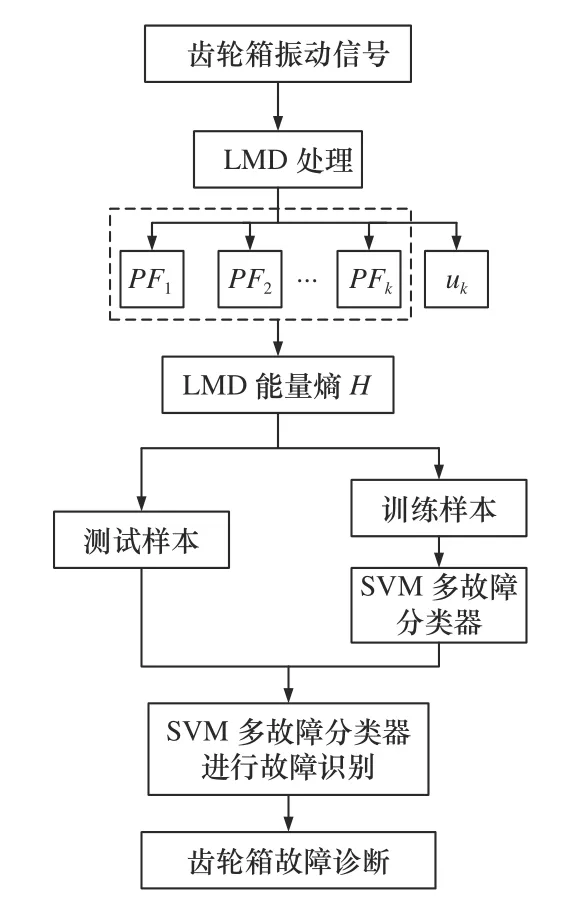
圖1 齒輪箱故障診斷步驟

為了實(shí)現(xiàn)齒輪箱故障診斷，首先在模擬實(shí)驗(yàn)臺(tái)上采集正常齒輪和不同故障齒輪振動(dòng)信號(hào)；然后采用LMD 方法對(duì)采集的每組振動(dòng)信號(hào)進(jìn)行分析和處理，每組信號(hào)由LMD 分解后分別得到k個(gè)PF 分量和一個(gè)殘余量uk(t)；其次將k個(gè)PF 分量作為分析對(duì)象，求出每個(gè)分量對(duì)應(yīng)的能量值，并通過(guò)上述公式計(jì)算出每組信號(hào)的LMD 能量熵；最后，從每種運(yùn)行狀態(tài)中選取一定數(shù)量信號(hào)的能量熵作為訓(xùn)練樣本輸入到SVM 多故障分類器中進(jìn)行訓(xùn)練，把每種狀態(tài)剩下信號(hào)的能量熵作為測(cè)試樣本輸入到訓(xùn)練后的SVM 分類器中進(jìn)行分類測(cè)試，依據(jù)測(cè)試結(jié)果得出診斷精度和方法有效性。

3 實(shí)驗(yàn)分析

根據(jù)常用齒輪箱結(jié)構(gòu)，選擇在QPZZ-Ⅱ旋轉(zhuǎn)機(jī)械故障模擬試驗(yàn)臺(tái)采集正常齒輪和不同故障齒輪振動(dòng)信號(hào)，并以此檢驗(yàn)出LMD 能量熵和SVM 方法的診斷效果。QPZZ-Ⅱ試驗(yàn)臺(tái)主要由驅(qū)動(dòng)電機(jī)、聯(lián)軸器、齒輪箱和磁粉扭力器等零件構(gòu)成，裝置實(shí)物圖如圖2 所示。

圖2 旋轉(zhuǎn)機(jī)械故障模擬試驗(yàn)臺(tái)

實(shí)驗(yàn)過(guò)程中，為了能有效采集到最真實(shí)的齒輪箱振動(dòng)信號(hào)，在試驗(yàn)臺(tái)齒輪箱蓋的頂部和側(cè)面中心位置分別安裝1 個(gè)加速度傳感器，并使用ADA16-8/2(LPCI)采集卡來(lái)采集齒輪箱振動(dòng)信號(hào)，具體齒輪箱故障模擬實(shí)驗(yàn)裝置簡(jiǎn)圖如圖3 所示。振動(dòng)信號(hào)采集過(guò)程中，除了采集無(wú)故障正常齒輪振動(dòng)信號(hào)以外，還根據(jù)實(shí)際需要，在齒輪箱中更換了不同故障齒輪來(lái)模擬故障信號(hào)，具體包括大齒輪磨損、小齒輪斷齒、大齒輪磨損+小齒輪斷齒3 種故障齒輪，正常齒輪與故障齒輪均為標(biāo)準(zhǔn)直齒輪，且材質(zhì)、模數(shù)均相同，實(shí)例齒輪箱參數(shù)如表1 所示。其中，齒輪磨損是在正常大齒輪基礎(chǔ)上利用磨齒機(jī)將齒輪齒面單邊打磨掉0.2 mm 厚度來(lái)模擬磨損故障；斷齒是在正常小齒輪基礎(chǔ)上利用銑床銑掉一個(gè)齒來(lái)模擬出斷齒故障，實(shí)驗(yàn)齒輪如圖4 所示。

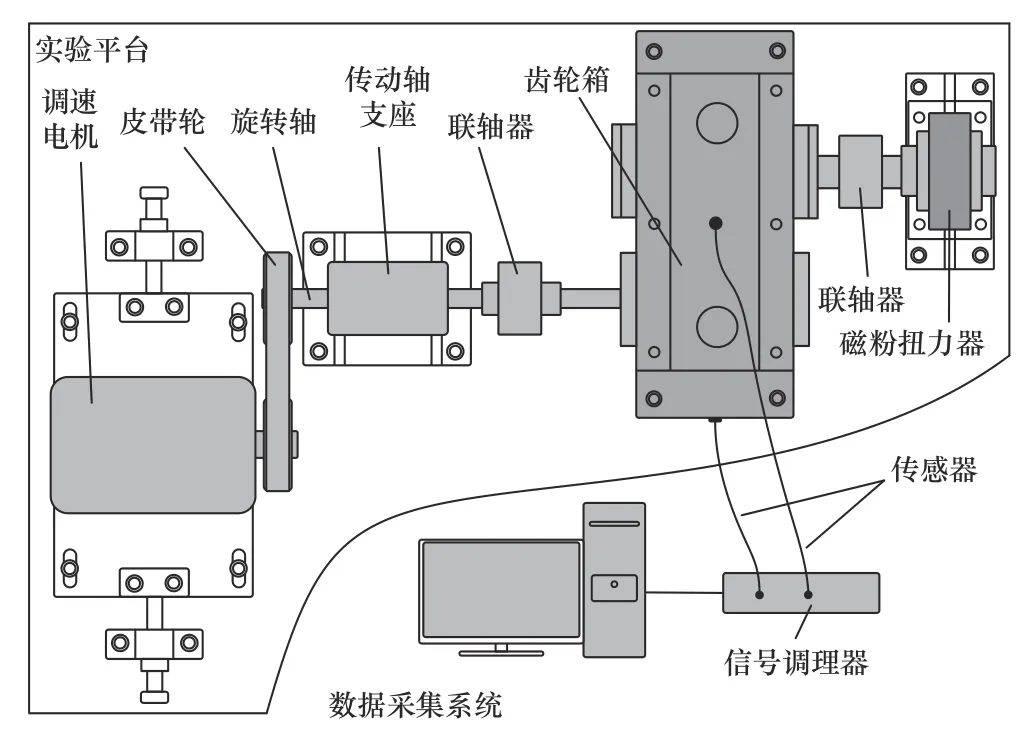
圖3 齒輪故障模擬實(shí)驗(yàn)裝置簡(jiǎn)圖

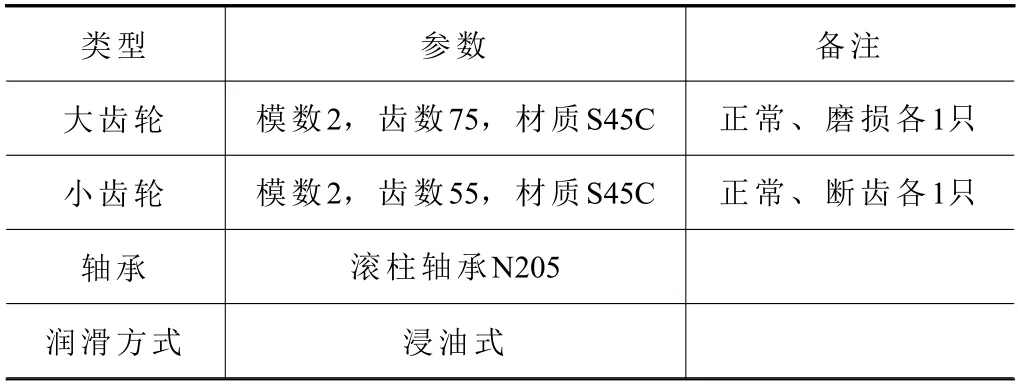
表1 實(shí)例齒輪箱參數(shù)

圖4 實(shí)驗(yàn)齒輪

實(shí)驗(yàn)過(guò)程中，驅(qū)動(dòng)電機(jī)平均轉(zhuǎn)速為1 470 r/min，設(shè)置采樣頻率為5 120 Hz、采集點(diǎn)數(shù)為2 000，同樣條件下分別對(duì)4 種齒輪箱工作狀態(tài)振動(dòng)信號(hào)進(jìn)行采樣，為滿足小樣本條件需求（樣本不多于30），每種工作狀態(tài)下各采集20 組振動(dòng)數(shù)據(jù)。

實(shí)驗(yàn)數(shù)據(jù)采集后，對(duì)各組齒輪箱振動(dòng)信號(hào)進(jìn)行LMD 分析，分解后得到若干PF 分量和最終殘余量。圖5 以一組磨損+斷齒故障為例，原始振動(dòng)信號(hào)經(jīng)LMD 分解后得到5 個(gè)PF 分量和1 個(gè)殘余分量。從圖中可以看出，LMD 分解得到的PF 分量將原始信號(hào)按照從大到小順序分解出信號(hào)的分辨率，殘余量u5(t)振動(dòng)極其微弱，能量可忽略不計(jì)。分別對(duì)正常和3 種故障齒輪振動(dòng)信號(hào)進(jìn)行LMD 分解，并求出PF 分量能量及對(duì)應(yīng)的能量熵。

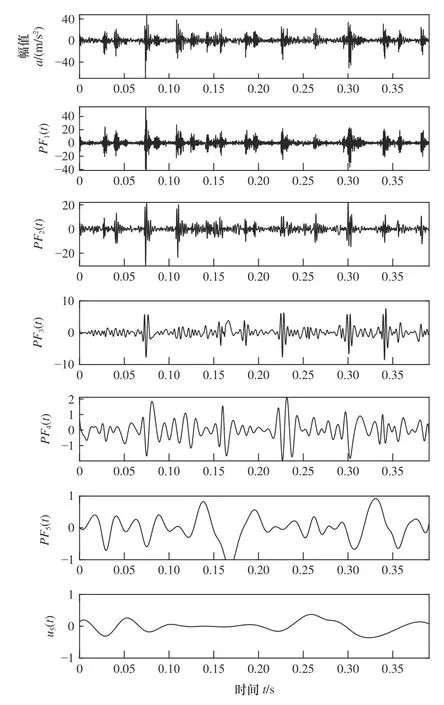
圖5 磨損+斷齒狀態(tài)原始振動(dòng)信號(hào)及LMD 分解結(jié)果

隨機(jī)從4 種狀態(tài)中分別選取出10 組振動(dòng)信號(hào)作為SVM 訓(xùn)練樣本數(shù)據(jù)，圖6 為40 組信號(hào)經(jīng)LMD分解后得到的5 個(gè)PF 分量能量值分布情況。從圖中可以看出，雖然每種狀態(tài)經(jīng)LMD 分解后的PF 分量能量值整體分布在一定數(shù)值區(qū)間內(nèi)，但都會(huì)出現(xiàn)跳躍現(xiàn)象，即不同工作狀態(tài)下的PF 能量值會(huì)存在交叉重合。出現(xiàn)這一情況的主要原因是當(dāng)齒輪產(chǎn)生故障時(shí)，振動(dòng)引起的能量存在交叉，如斷齒與無(wú)故障齒輪相比，齒輪旋轉(zhuǎn)一圈存在一次斷齒部位振動(dòng)突變但缺少一次齒輪嚙合振動(dòng)，整體能量差別較小；齒輪出現(xiàn)磨損故障時(shí)，因磨損為每個(gè)齒面均勻磨損，嚙合頻率及其諧波分量幅值增加，且高次諧波幅值增加更多，甚者出現(xiàn)分?jǐn)?shù)諧波，因此磨損故障對(duì)應(yīng)能量較大；而磨損+斷齒相對(duì)于磨損故障，前者每旋轉(zhuǎn)一圈的斷齒部位突變和磨損嚙合突變相近，且每圈少一齒嚙合振動(dòng)，因而前者能量相對(duì)后者較小，但相對(duì)于斷齒，因前者有部分磨損故障，因此能量大于斷齒故障。但是，從圖7 中上述40 組信號(hào)計(jì)算出的LMD 能量熵值分布情況可以看出，即使經(jīng)LMD 分解后的PF分量能量值出現(xiàn)跳躍和相互交叉，每種狀態(tài)振動(dòng)信號(hào)對(duì)應(yīng)的LMD 能量熵卻呈現(xiàn)出顯著的分布規(guī)律。

圖6 訓(xùn)練樣本PF 能量值分布圖

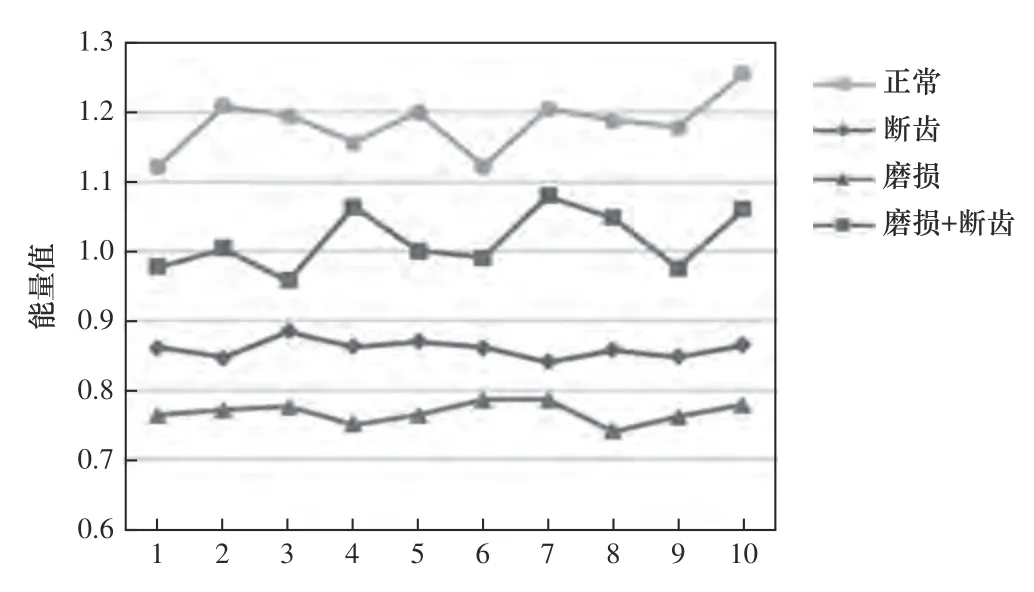
圖7 訓(xùn)練樣本LMD 能量熵值分布圖

同時(shí)，從圖7 中的LMD 能量熵分布情況能夠看出，未發(fā)生故障的正常齒輪振動(dòng)信號(hào)對(duì)應(yīng)的LMD 能量熵值比故障齒輪對(duì)應(yīng)的值高，原因是齒輪箱未出現(xiàn)故障時(shí)，整體運(yùn)行相對(duì)較為平穩(wěn)，振動(dòng)信號(hào)在不同頻域區(qū)域內(nèi)分布也相對(duì)均衡，能量在各頻率區(qū)域的不確定性程度相對(duì)較大，對(duì)應(yīng)的LMD能量熵值也就較大。當(dāng)齒輪箱發(fā)生故障時(shí)，振動(dòng)頻率會(huì)有部分集中分布在對(duì)應(yīng)的故障共振頻率區(qū)間內(nèi)，因此振動(dòng)信號(hào)的能量會(huì)在故障頻域范圍內(nèi)集中，能量在各頻域區(qū)域的不確定性程度相對(duì)較小，故對(duì)應(yīng)的LMD 能量熵低于正常狀態(tài)下的。而且，當(dāng)齒輪箱出現(xiàn)磨損故障，其每一個(gè)齒面都是均勻磨損，每次嚙合振動(dòng)頻率相對(duì)一致，不確定性最小，因此能量熵最小；當(dāng)齒輪箱出現(xiàn)斷齒故障，斷齒嚙合前后振動(dòng)與正常齒輪相近，但斷齒嚙合過(guò)程存在不同振動(dòng)頻率，振動(dòng)頻率相對(duì)磨損復(fù)雜，不確定性大于磨損，能量熵也就大于磨損狀態(tài)下；當(dāng)齒輪箱同時(shí)出現(xiàn)磨損和斷齒兩種故障時(shí)，振動(dòng)信號(hào)會(huì)在上述兩種故障頻域上分散，振動(dòng)頻率復(fù)雜程度高于斷齒和磨損，不確定性也大于斷齒和磨損任一故障，因此磨損+斷齒狀態(tài)下的LMD 能量熵值要比單獨(dú)故障狀態(tài)下的高。

在完成故障特征分析和提取后，為了實(shí)現(xiàn)齒輪箱故障分類，將4 種狀態(tài)下隨機(jī)選取的10 組振動(dòng)信號(hào)LMD 能量熵輸入到由4 個(gè)SVM 組成的多故障分類器內(nèi)展開(kāi)訓(xùn)練；將每種狀態(tài)下剩余的10 組振動(dòng)信號(hào)作為測(cè)試樣本輸入到訓(xùn)練后的SVM 多故障分類器內(nèi)展開(kāi)分類和識(shí)別，識(shí)別結(jié)果如表2 所示。從表2 識(shí)別結(jié)果能夠看出，4 種狀態(tài)識(shí)別精度均為100%，充分說(shuō)明了基于LMD 能量熵和SVM 方法對(duì)齒輪箱故障診斷的優(yōu)越性。

表2 基于LMD 能量熵和SVM 方法識(shí)別結(jié)果

4 結(jié)語(yǔ)

本文介紹了基于LMD 能量熵和SVM 故障診斷方法，并運(yùn)用該方法對(duì)齒輪箱故障進(jìn)行了分類和識(shí)別，得出了如下結(jié)論：

（1）LMD 能量熵對(duì)非線性信號(hào)具有很高的表征能力，能夠有效提取出齒輪箱故障特征。

（2）基于LMD 能量熵和SVM 方法對(duì)小樣本故障診斷具有較強(qiáng)的優(yōu)勢(shì)，實(shí)驗(yàn)結(jié)果表明，該方法能有效、準(zhǔn)確地對(duì)齒輪箱故障分類和識(shí)別。

（3）基于LMD 能量熵和SVM 方法對(duì)已知故障診斷效果較好，對(duì)未標(biāo)識(shí)故障樣本及相關(guān)領(lǐng)域診斷效果還需進(jìn)一步驗(yàn)證和研究。