基于改進粒子群算法數控磨床可靠性分配優化研究

范晉偉 劉會普 張理想 李偉華

（①北京工業大學機械工程與應用電子技術學院，北京 100124；②北京第二機床廠有限公司，北京 102444）

數控磨床作為集機、電、液和光于一體的現代化制造裝備，主要應用于航空、航天和汽車等高精密工件的加工上，由于本身集成的復雜性，就會對其可靠性提出較高的要求[1]。在機電產品設計中，可靠性的分配與優化是整機可靠性設計的重要工作。

國內外學者對可靠性分配方法進行了大量的研究工作：陳一凡等人基于元動作理論建立了元動作與數控機床可靠性的映射關系，并利用sobol 法進行了求解[2]。王琪瑞基于AGREE 分配法對四路能源模塊功率合成系統進行了可靠性分配和優化[3]。程強等人采用直覺梯形模糊數和層次分析法，提出了一種新的數控機床可靠性分配方法[4]。武保林等人使用遺傳算法對電動飛機手操作系統進行了可靠性分配[5]。以上可靠性分配方法為數控磨床可靠性分配方法提供了參考，但目前可靠性分配方法依舊存在以下關鍵問題需要進一步探究：

（1）上述方法多依賴專家意見的分配方法，主觀性過強。

（2）遺傳算法雖然能較好地解決可靠性優化分配問題，但存在高維問題收斂速度慢甚至很難收斂的缺點。

因此，文章提出了一種改進粒子群算法，對數控磨床可靠度-成本非線性規劃模型進行最優求解，實現了數控磨床可靠性的合理分配與優化。

1 基本理論

1.1 粒子群算法

粒子群算法（particle swarm optimization）源于對鳥群捕食行為的研究，其基本思想是通過群體中個體之間的協作和信息共享來尋求最優解[6]。

粒子群算法通過設計一種無質量的粒子來模擬鳥群中的鳥，粒子僅具有兩個屬性：速度v和位置x，速度代表移動的快慢，位置代表移動的方向。每個粒子在搜索空間中單獨的搜尋最優解，并將其記為當前個體極值，并將個體極值與整個粒子群里的其他粒子共享，找到最優的個體極值作為整個粒子群的當前全局最優解，粒子群中的所有粒子根據自己找到的當前個體極值和整個粒子群共享的當前全局最優解來調整自我速度和位置。速度v和位置x更新公式如下[7]。

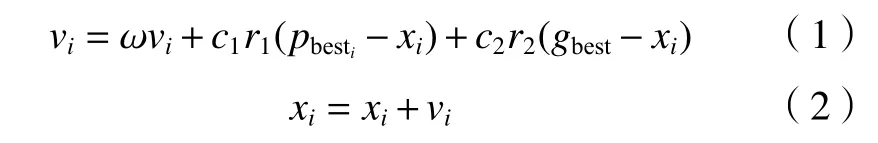
式中：vi為第i個粒子的速度；ω為慣性因子，取值范圍[0,1],決定全局尋優能力的強弱；c1、c2為學習因子，通常取0.5；r1、r2為 [0,1] 的隨機數；pbesti為第i個粒子本身經歷過的最優位置；gbest為粒子群經歷過的最優位置；xi為第i個粒子的位置。

事實上，式（1）的第一部分為“慣性項”，即粒子有維持自我之前運動的趨勢；第二部分為“自我認知項”，即粒子有向自我歷史最佳位置方向逼近的趨勢；第三部分為“群體認知項”，即粒子有向群體歷史最佳位置方向逼近的趨勢。式（2）表示在第i次尋優時的位置更替。更新過程如圖1所示。

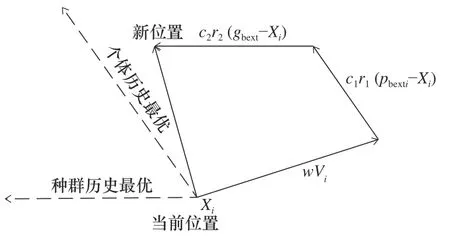
圖1 粒子群算法位置更新圖

1.2 改進粒子群算法

在工程實踐中，約束優化問題最為常見，通常表示為如下形式。

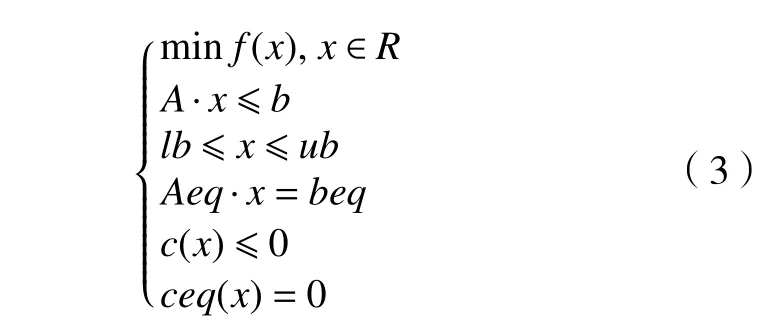
式中：f(x)為 目標函數，一般求其最小值，A·x≤b和lb≤x≤ub為線性不等式約束，Aeq·x=beq為線性等式約束，c(x)≤0為 非線性不等式約束，ceq(x)=0為非線性等式約束。

由粒子群算法的更新過程可知，其更新過程并未涉及約束條件，這使得傳統粒子群算法并不能很好解決上述約束優化問題。因此，文章結合懲罰函數法，提出了一種改進粒子群算法，其流程圖如圖2 所示。

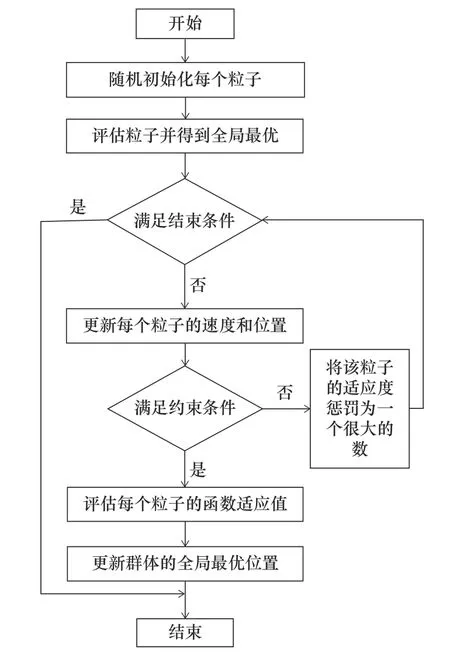
圖2 改進粒子群算法流程圖

2 可靠度-成本函數模型

2.1 現有可靠度-成本函數模型

（1）對數模型

有些學者將系統可靠度與成本之間的關系歸納為對數關系[8-10]。

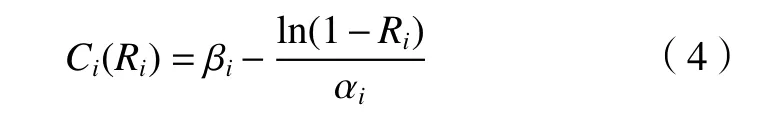
式中：Ci為子系統i的成本，Ri為子系統i的可靠度，βi為子系統i的初始成本，αi為子系統i的結構復雜度，取值區間為（0，1）。

由圖3 可以看出：在系統結構復雜度不變的情況下，隨著可靠度的增長，實際成本呈非線性增長。在可靠性不變的情況下，隨著結構復雜度的增大，實際成本呈減小趨勢，這與實際情況是不符的。

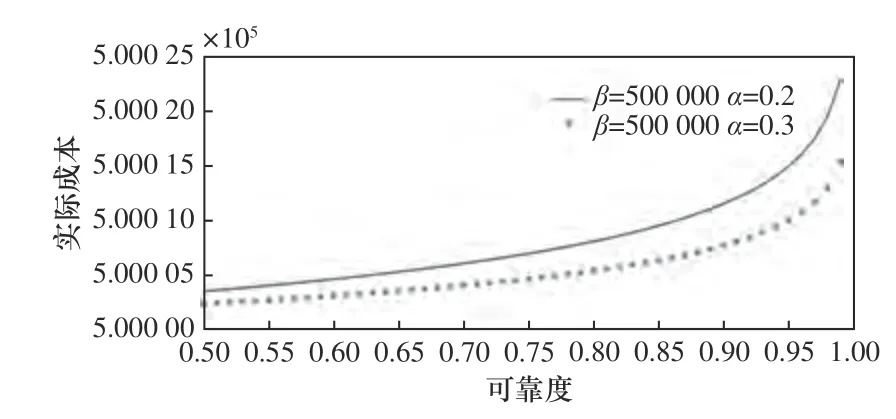
圖3 對數模型可靠度-成本圖

（2）冪函數模型

冪函數模型公式如下[11]。

式中：Ki和 αi為與系統結構的常數，由于這兩個參數的確定需要長期的經驗積累，獲取較為困難，且該方法缺乏通用性，故不考慮該方法確定數控磨床的成本模型。

（3）指數模型

指數模型公式如下[12]。

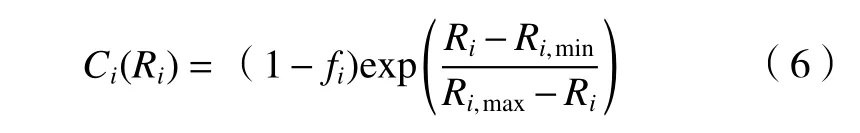
式中：fi為子系統i的可行度，取值區間(0,1)，其值越大，代表改進該系統可靠度對提升整機可靠度的可行性越大；Ri,min為子系統i在數控磨床工作一段時間后，根據故障間隔時間分布模型求解出的現有可靠度；Ri,max為在現有技術條件下，系統能達到的最大可靠度。

2.2 改進可靠度-成本函數模型

根據可靠性分配的特點，恰當改進成本函數可以描述各種影響因素與成本之間的關系，在可靠性分配中體現各種因素的影響[13]。因此，結合現有函數模型，引入敏感度因子si對可靠度-成本函數模型進行改進

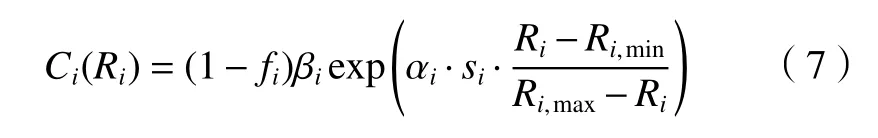
式中：si越大，代表整機可靠度的變化對第i個子系統可靠度的變化越敏感；fi為子系統i的可行度，取值區間（0,1）；αi為子系統i的結構復雜度；βi為子系統i的初始成本；Ri,min、Ri,max分別為子系統i可靠度的上下限；Rs(t)為 數控磨床整機的可靠度，Ri(t)為子系統i的可靠度。

圖4 描繪的為不同敏感度因子si對應的圖像，從圖中可以看出：在可靠度較低的情況下（R＜0.65），敏感度因子的差異對實際成本的影響很小；隨著可靠度的增長，實際成本呈非線性增長，且在可靠度增長后期，圖像斜率明顯增加，即實際成本激增，符合實際工程情況。

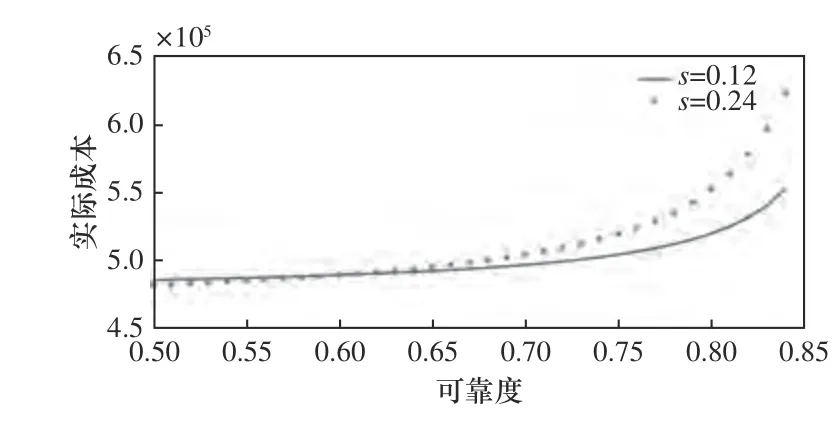
圖4 改進可靠度-成本模型圖

3 實例分析

3.1 數控磨床可靠性分配模型

建立整機的可靠度分配模型之前首先需要對各子系統進行描述，便于確定各子系統之間的關系。文章根據數控磨床的結構特點、磨床生產廠家的共識及磨床在設計、制造和外購外協時的功能將數控磨床分為9 個子系統，如表1 所示，以此為基礎建立了數控磨床工作時的連接框圖，如圖5 所示。

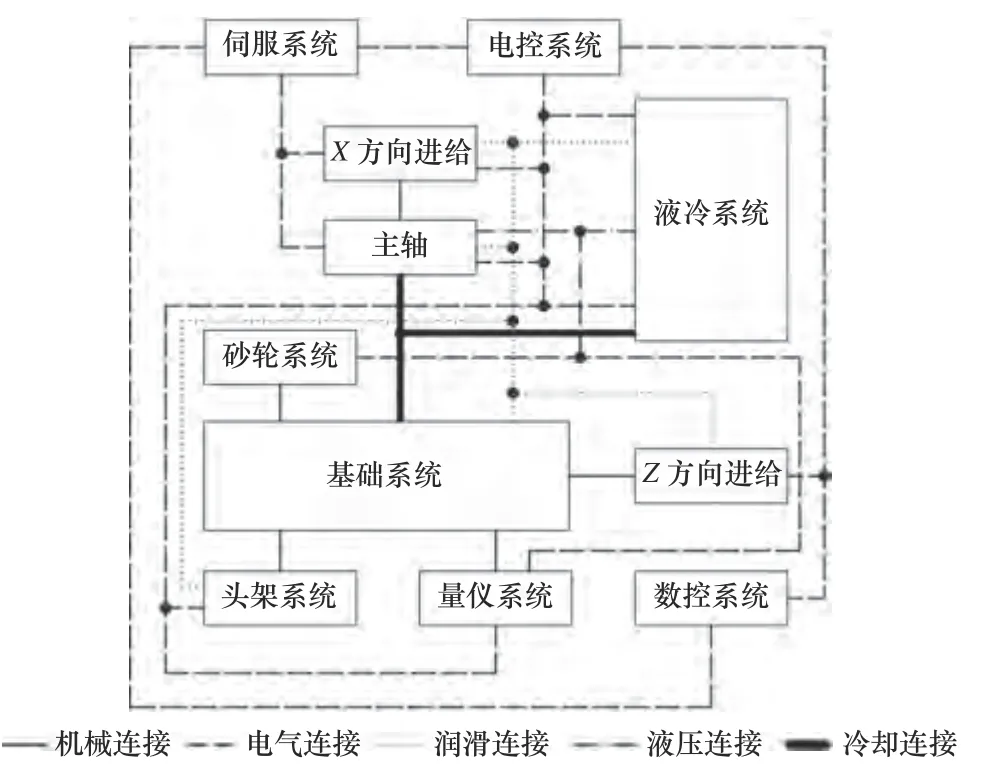
圖5 數控磨床子系統工作連接圖

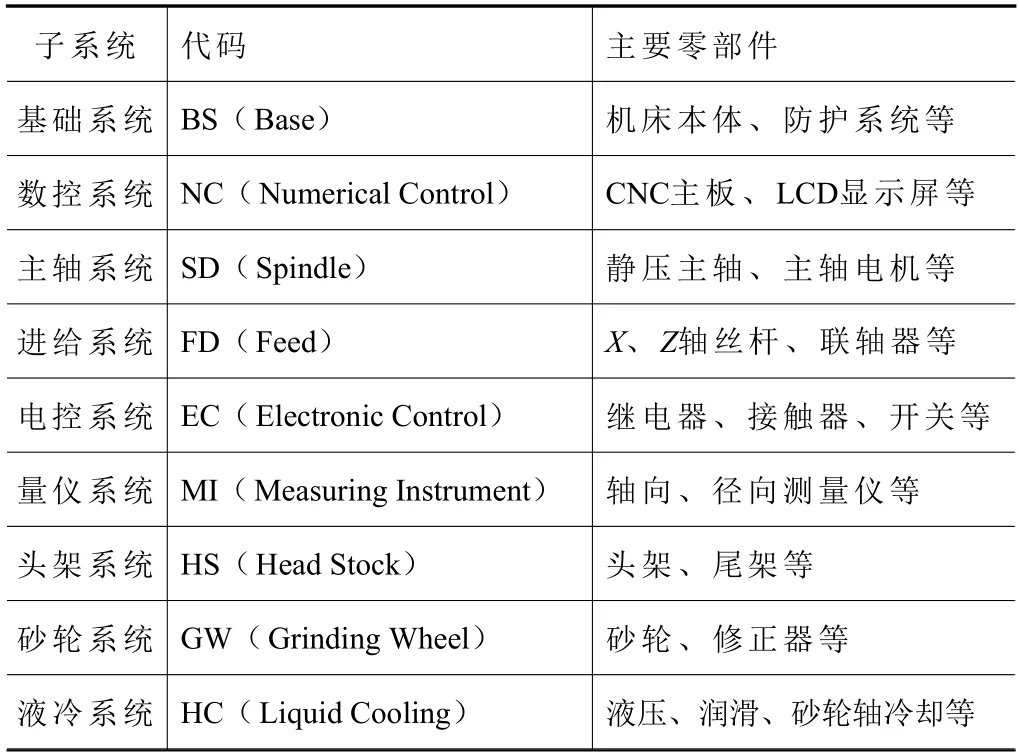
表1 數控磨床子系統主要零部件表

從圖5 中可以看出，數控磨床9 個子系統之間多為串聯關系，事實上，數控磨床作為一個復雜的電氣液系統，許多學者把數控磨床各子系統之間歸納為串聯關系[14-16]，按照表1 中順序將各子系統編號為1～9，設Ri為第i個子系統的可靠度，結合子系統串聯關系，則數控磨床整機的可靠度Rs可以表示為

以成本最小為目標函數，建立可靠性分配模型，得

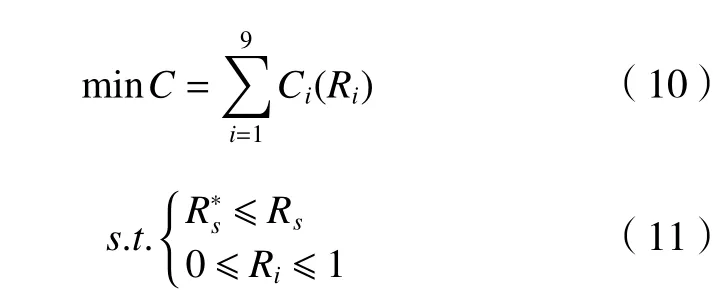
3.2 改進粒子群算法求解

采用MATLAB 對改進粒子群算法對數控磨床可靠性分配模型進行求解，算法中初始個體數為500，最大迭代次數為200，慣性因子取0.8，自我學習因子和群體學習因子均取0.5，各子系統可靠度參數及分配結果如表2 所示。

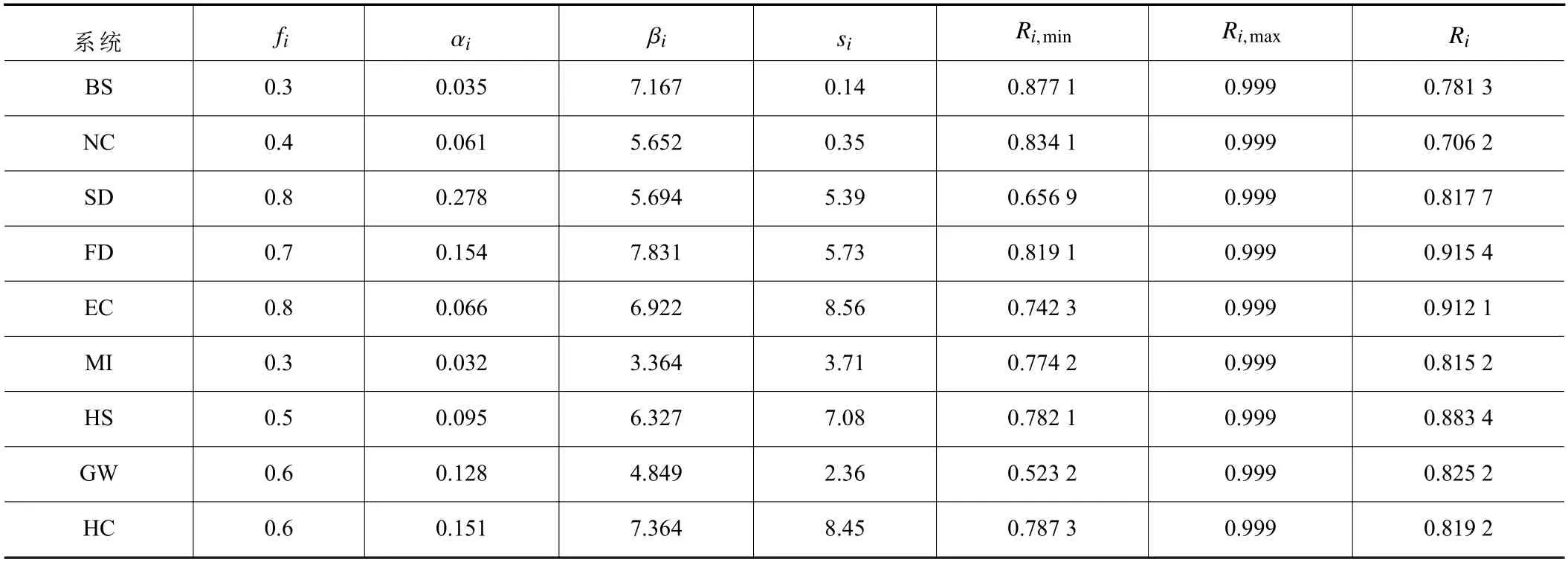
表2 數控磨床可靠度分配最優解

圖6 為改進粒子群算法求解的收斂過程，從圖像中可以看出，在迭代次數為37 左右時，算法已經趨于最優解41.047，迭代速度理想。

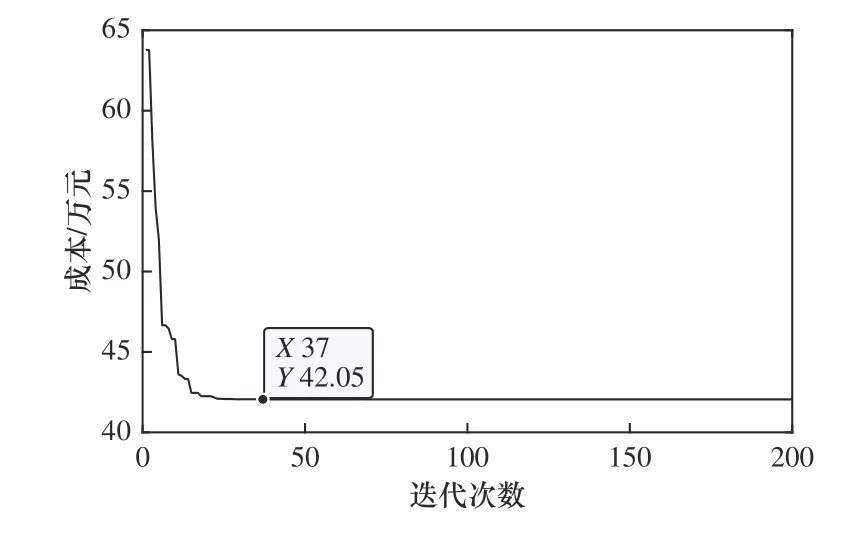
圖6 改進粒子群算法收斂曲線

3.3 對比

為比較改進粒子群算法與遺傳算法的優劣，將本文的結果與文獻[17]對比，對比結果如表3 所示。

從表3 可靠度角度來看，在1 000 h 時，數控磨床整機系統可靠度現有水平為0.072 9，利用遺傳算法優化后整機系統可靠度為0.183 4，以該值為設計標準，利用改進粒子群算法優化：從成本角度來看，數控磨床整機成本現有水平為55.17 萬元，利用遺傳算法使整機成本降為42.901 萬元，降幅約為22.24%，利用改進粒子群算法使整機成本降為41.047 萬元，降幅約為25.60%，優化效果更明顯。

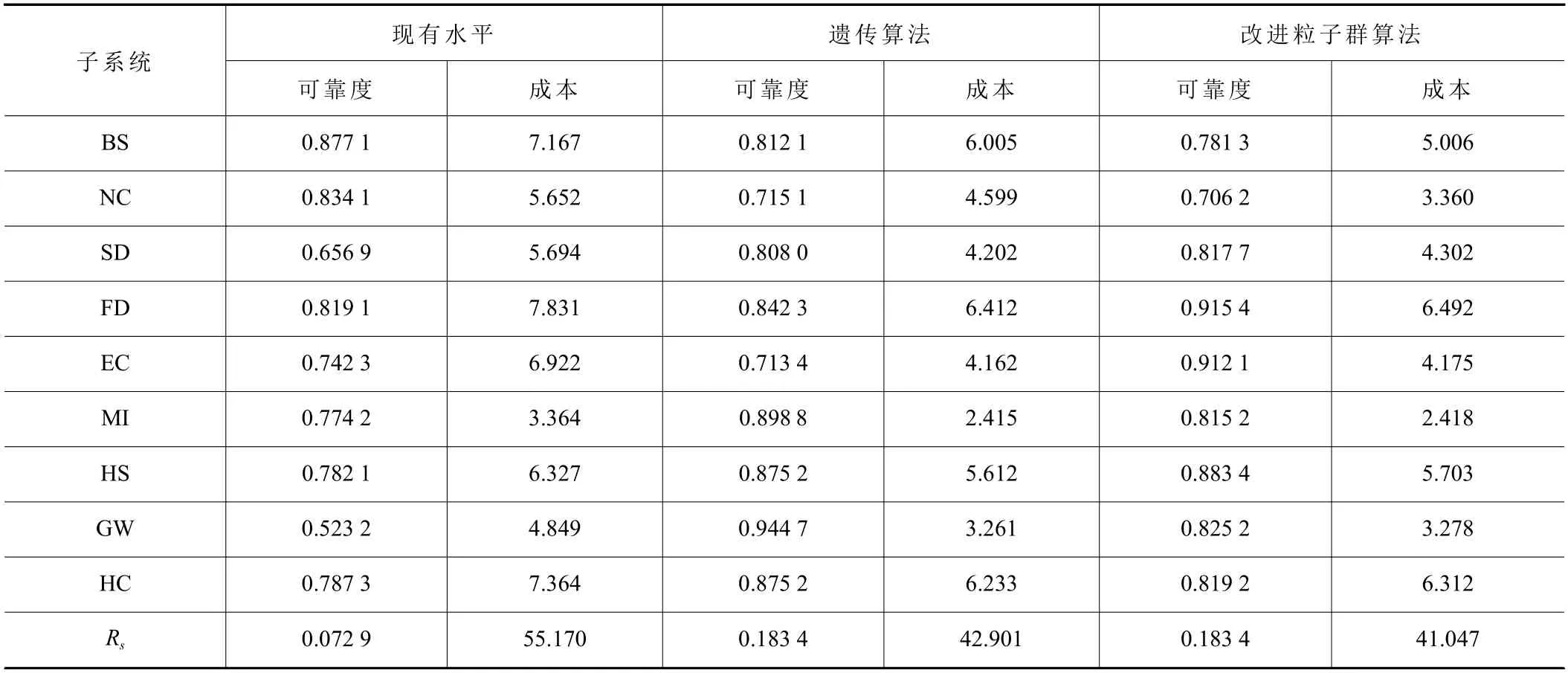
表3 不同優化方法的可靠度與成本 萬元

4 結語

針對數控磨床可靠性分配優化問題，文章提出了一種能夠解決帶有非線性不等式約束條件的粒子群算法。在現有可靠度-成本函數模型基礎上，引入敏感度因子si構建了數控磨床可靠性分配優化模型，利用改進粒子群算法對模型進行求解并與相關文獻作對比，結果顯示：改進粒子群算法優化分配結果更加合理。優化結果已反饋給廠家并獲得認可，對提升數控磨床整機的可靠性水平有重要意義。