基于改進遺傳算法的自由曲面測量路徑優化＊

徐傳法 王士軍 王 冉 李建宏 齊娜

（山東理工大學機械工程學院，山東 淄博 255000）

隨著科學技術的不斷進步，機械產品的結構越來越合理，復雜曲面類零件被廣泛的應用在動力能源、航空航天和工業等領域，其形狀誤差對其所構成產品的質量和性能起著直接的決定性作用，研究高效率、高精度的測量技術具有重要的理論意義和實際應用價值[1]。在對大型復雜曲面測點檢測時，曲面需要被檢測的點是非常多的，為了提高檢測效率，需要找到一條最優的檢測路徑，既能不重復的走過所有的點，還要使其走過的路徑最短。

國內外學者對于路徑優化問題方面做了許多的研究。高延峰等將遺傳算法運用到求解自由曲面測量路徑優化問題上，把該問題簡化成旅行商問題，試驗證明遺傳算法結構簡單而且具有很強的優化能力[2]；高國軍等提出了貪婪選擇雜交算子，有效地提高了大規模路徑優化的收斂速度和穩定性，并且對遺傳算法過程中的控制參數進行了優化，給出了適合不同規模路徑優化問題的控制參數取值[3]；Tuncer D 等提出了改進的變異算子，避免早熟的同時提高了算法的效率[4]；Srinivas M 等提出了自適應算法，個體的交叉概率能夠隨個體的適應度發生改變，防止陷入局部最優的同時提高了算法的效率[5]；石紅國等提出一種 Hopfield 神經網絡與歸約方法相結合求解TSP 路徑優化的方法，使Hopfield 神經網絡不再只適用于求解小規模城市路徑優化問題[6]。

文獻[2]中，把遺傳算法運用到自由曲面測量路徑優化問題中，但并未對遺傳算法收斂速度慢、易陷入局部最優解等問題做更深入研究，基于以上問題，本文設計了改進的遺傳算法，實驗結果表明，改進的遺傳算法能夠更高效且優質地完成自由曲面測量路徑優化問題。

1 自由曲面的測點檢測過程

三坐標測量機測點檢測過程中測頭的具體運動過程如圖1 所示。首先測頭快速定位到A點，再以檢測速度沿路徑AB往B點移動，當檢測完B點后，再以回退速度移動到C點，然后測頭再快速定位到D點重復剛才的運動過程。無論檢測路徑如何變化，AB段（a段）與BC段（b段）的運動過程總是固定不變的，為簡化求解過程，不考慮測量過程a與回退過程b這種固定不變的路徑，只計算c這種影響總路程的路段，此時的測點檢測過程就被簡化成了類旅行商（TSP）問題。

圖1 局部檢測路徑示意圖

自由曲面測點檢測過程與旅行商問題的主要區別在于：

（1）當測頭檢測完最后一個測點時，測頭不需要回到初始測點。

（2）旅行商問題中用到的城市坐標是二維坐標，而自由曲面測點的坐標是三維的。

2 遺傳算法簡介

遺傳算法（genetic algorithm，GA）最早是由美國的 John Holland 于20 世紀70 年代提出，該算法效仿大自然“物競天擇，適者生存”的演化規律來求解各類問題。遺傳算法把問題參數編碼為基因，把問題的解編碼為染色體，然后對各個染色體進行選擇、交叉和變異等操作，通過迭代來不斷優化各個染色體中的信息，以優勝劣汰的方式最終生成一條較優的染色體作為問題的解。

3 改進遺傳算法的設計

3.1 編碼方式

采用自然編碼方式，每個自然數表示1 個要檢測的測點，例如一個染色體的基因串為26 379，則表示測頭從2 號測點出發，順序經過6、3、7、9號測點完成該條路徑的檢測。

3.2 適應度函數

遺傳算法在尋求最優解的過程中僅依據適應度函數來選擇優質解和淘汰劣質解，算法的求解質量和求解效率與適應度函數的選取密不可分。由于影響總路程變化的只有像c這樣的路徑段，所以求得的目標函數為，目標函數越小，優化的結果越好，輪盤賭選擇算子個體適應度值越大，被選擇的概率越高，所以對目標函數做了一次倒數轉換，轉換后用作適應度函數

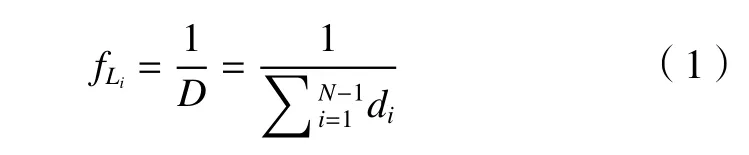
3.3 選擇算子

采用輪盤賭選擇算子，輪盤賭算法的基本思想是：各個個體被選中的概率與其適應度函數值大小成正比，它是為了防止適應度數值較小的個體被直接淘汰而提出的。它的實施步驟為：

（1）計算種群中各個個體的適應度。

（2）通過式（2）與式（3）分別計算各個個體的被選擇概率和累計概率。

（3）在區間[0,1]隨機選取1 個數x，x落在哪個個體的累計概率區間內，則該個體被選中。

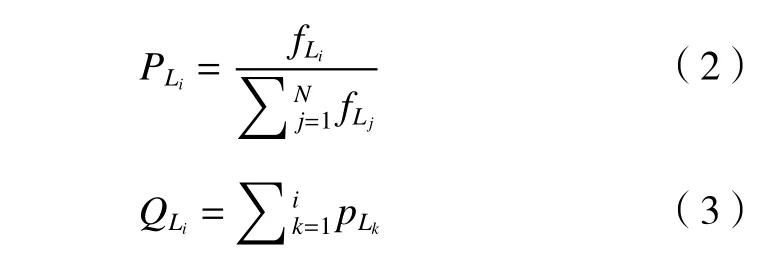
3.4 自適應參數調節

交叉概率和變異概率對遺傳算法的性能有著重要的影響，選擇合適的交叉概率和變異概率，有利于提高種群的尋優效率和防止局部最優解的出現。在傳統的遺傳算法中，交叉概率和變異概率在算法迭代過程中是固定不變的，這樣不利于遺傳算法更好地發揮其性能。許多學者對參數的自適應調節做了研究[7-9]，在此基礎上，本文對交叉概率和變異概率的自適應參數調節做了如下設置。

3.4.1 自適應交叉概率調節機制

在種群進化初期，種群個體的適應度比較分散，為增加新個體的產生速度，加快種群整體搜索效率，應該增大Pc的值；在種群進化后期，種群個體適應度比較集中，為使優良個體不被破壞，應該減小Pc的值；另外交叉算子有可能會破壞種群中的優良基因，為使交叉算子能夠更好地工作，對適應度差的個體，給與較高的Pc值，使其能夠更好地進化；對適應度高的個體，應該減小Pc的值，使優良的基因得以延續；文獻[9]以迭代次數作為進化處于何種階段的評判依據，對終止代數的選取是十分苛刻的，代數設置的太大會對自適應參數調節產生很大的影響。如圖2 所示。

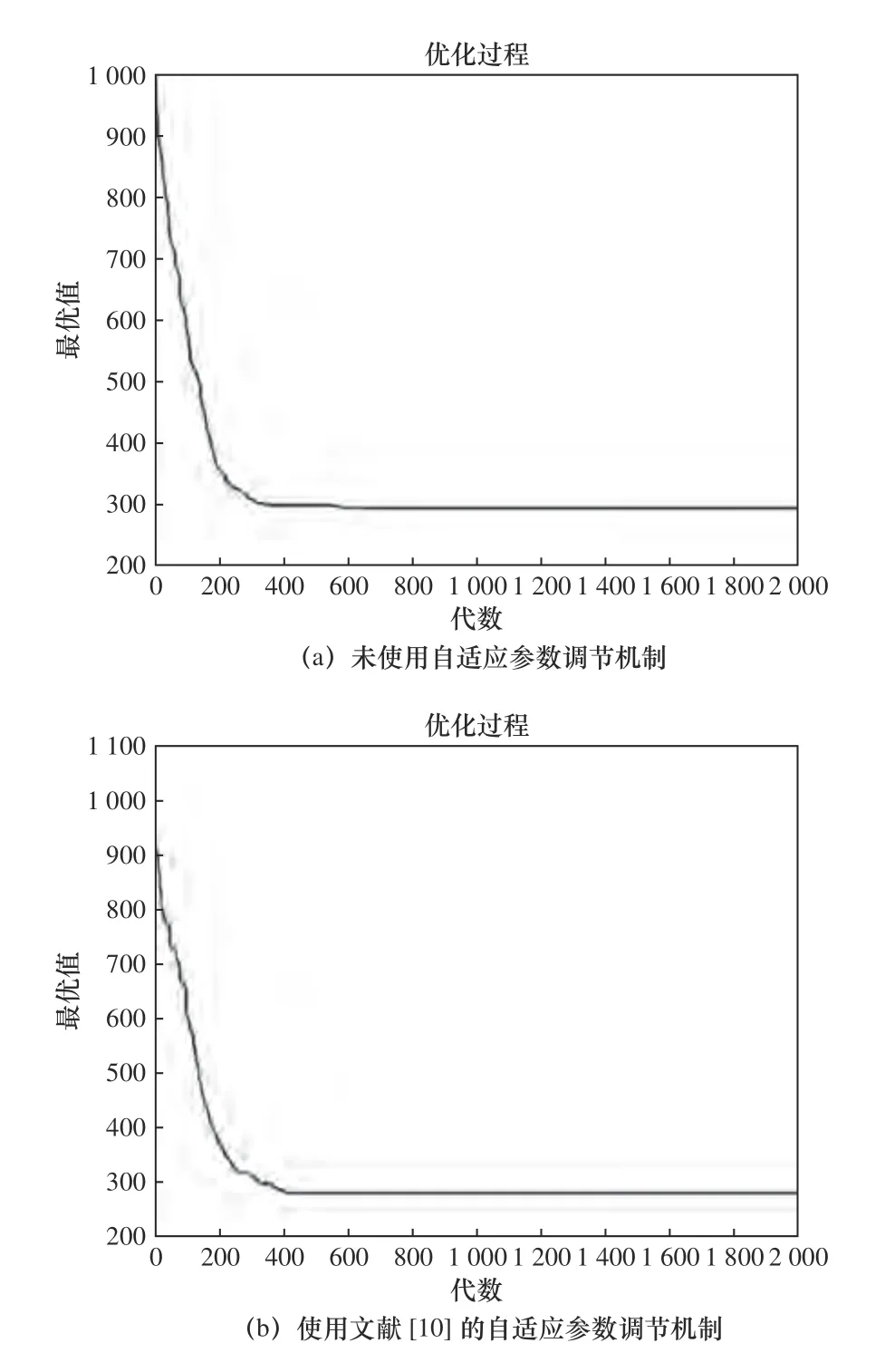
圖2 優化過程

對50 個城市尋求最優路徑，在遺傳算法其他部分相同的情況下，算法a 未使用自適應調節機制，算法b 使用文獻[9]的自適應調節機制，從圖2a 與b 的比較可知，在終止代數為2 000 的情況下，優化過程已無明顯差異，自適應參數調節機制幾乎失去作用。基于以上考慮，本文在文獻[9]的基礎上做了以下改進。

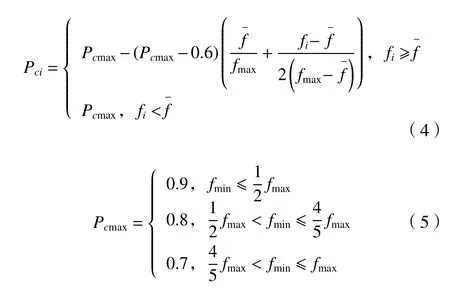
式中：Pci為種群中個體i發生交叉運算的概率；Pcmax與當前種群的適應度有關；fmax和fmin分別為當前種群最優個體的適應度和最差個體的適應度；fi為個體i的適應度值；為當前種群的平均適應度值。從式（5）可以看出Pcmax與當前種群個體的適應度分布情況有關。

改進后的自適應調節機制在遺傳算法其他部分與前面相同的情況下，對50 個城市尋求最優路徑，如圖3 所示。

圖3 使用改進的自適應參數調節機制

改進的自適應調節機制在終止代數為2 000 的情況下，依然能穩定地發揮其性能，不會因終止代數設置過大而導致自適應調節機制失效。

3.4.2 自適應變異概率調節機制

選取合適的變異概率，有利于保持種群多樣性和防止種群陷入局部最優。當種群中個體的適應度值沒有太大差距時，種群多樣性降低，易陷入局部最優，此時應該增大變異概率，通過變異增加種群多樣性，跳出局部最優。另外在種群進化過程中，為延續較優個體，應給與較優個體小的變異概率。基于以上考慮，本文在文獻[9]的基礎上做了以下改進。

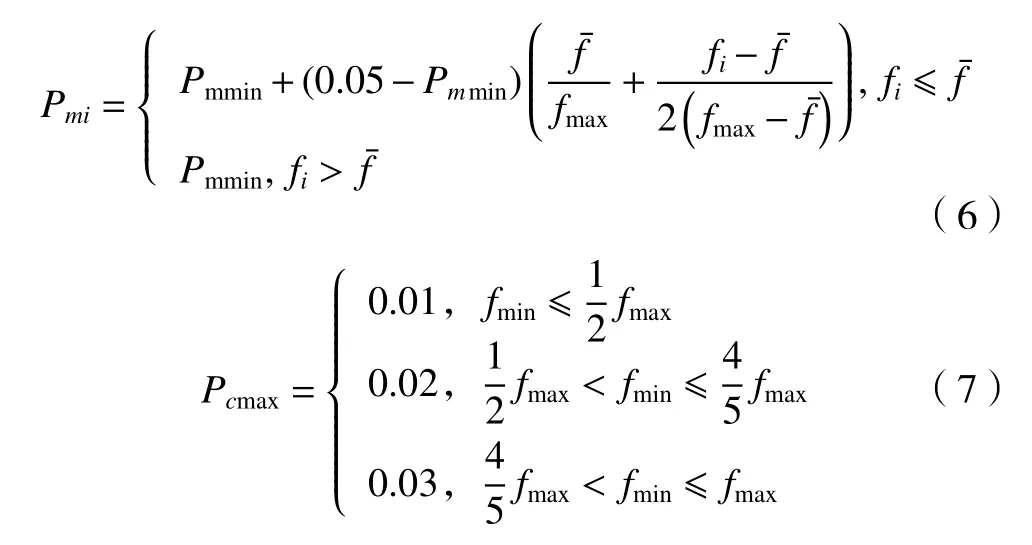
式中：Pmi為種群中個體i發生變異運算的概率；Pmmin與當前種群的適應度有關。

3.5 貪婪交叉算子

貪婪交叉算子能夠充分利用染色體的局部信息指導遺傳進化搜索。該算子在兩條父代染色體的兩個基因中使用局部貪婪策略得到一條新的染色體，這樣的子代染色體缺乏多樣性，容易陷入局部最優解。為防止局部收斂，另一條染色體由整體貪婪策略得到，增加群體多樣性。

假如參與交叉運算的父代個體為L1和L2，生成的子代個體為l1和l2，隨機產生的初始測點為Gstart。l1以Gstart為第一個監測點，分別計算父代中Gstart與與其右相鄰的兩個測點Gnext1與Gnext2之間的距離，若Gstart與Gnext1之間的距離小，則下一個測點選Gnext1，反之則選Gnext2，以此類推選出l1染色體上剩余的所有測點。l2的選取遵循整體貪婪策略的規則，以Gstart為第一個測點，計算Gstart與剩余所有測點之間的距離，選取與之距離最短的測點作為下一個測點，以此類推選出l2染色體上剩余的所有測點。

下面用7 個檢測點為例，說明貪婪交叉算子的運行過程。7 個測點的坐標分別為：1：（10，12，20），2：（41，26，23），3：（25，58，63），4：（81，55，42），5：（72，31，66），6：（55，43，82），7：（61，28，53），7 個測點之間的距離如表1 所示。

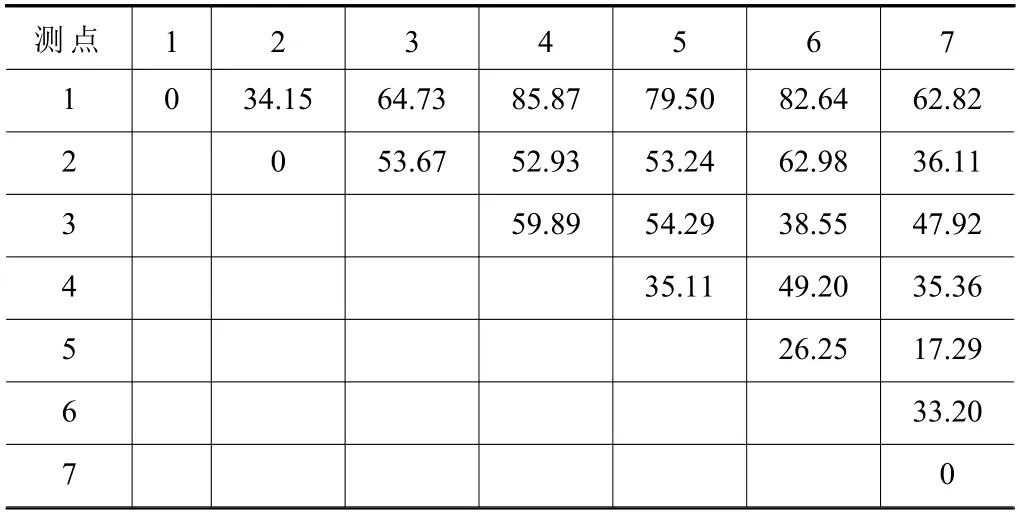
表1 7 個測點之間的距離

假設參加交叉運算的染色體L1和L2分別為（2 3 5 4 6 1 7）和（7 2 1 6 3 4 5），隨機產生初始測點為3，右轉動使3 成為初始測點。新生成L1'和L2'分別為（3 5 4 6 1 7 2）和（3 4 5 7 2 1 6），則l1的第一個基因為3，分別計算父代染色體中與測點3右相鄰的兩個測點的距離，得d35=54.29＜d34=59.89，則L1''和L2''分別為（3 5 4 6 1 7 2）和（3 5 4 7 2 1 6），l1的第二個基因為5，以此類推，得到的l1為（3 5 4 7 6 2 1）；l2由整體貪婪策略得到，計算測點3 與剩余所有測點之間的距離，d36＜d37＜d32＜d35＜d34＜d31，則l2的第二個基因為6，以此類推得到l2為（3 6 5 7 4 2 1）。

3.6 貪婪倒位變異算子

貪婪倒位變異算子是基于貪婪策略的倒位變異，首先在一條染色體上隨機選取一個基因Gx，計算該基因與左右相鄰兩基因Gxleft和Gxright之間的距離d1、d2，若d1＞d2,則選Gxleft為待變異基因，反之則選Gxright為待變異基因，再從除Gx、Gxleft和Gxright以外剩余的基因中，選取距離Gx最近的基因Gclose作為另一個待變異基因，在不改變其他基因位置的情況下，交換兩待變異基因位置，完成貪婪倒位變異運算。

以L1（2 3 5 4 6 1 7）為例，隨機選取的測點為3。先計算測點3 與左右相鄰兩測點之間的距離d32、d35，d35＞d32則第一個待變異測點為5，再從除3、2 和5以外的剩余測點中選取距離3 最近的基因作為另一個待變異基因，經計算得該基因為6，交換兩待變異基因的位置，得到變異后的染色體l1為(2 3 6 4 5 1 7)。

3.7 精英保存策略

為防止選擇過程中最優解的丟失和交叉變異過程中最優解的破壞，實施精英保存策略。通過選擇、交叉和變異后，復制子代中的最優個體并保存到下一輪的子代中，剩余子代繼續下一輪的選擇、交叉和變異，用復制的最優個體替代下一輪子代的最差個體。繼續實施精英保存策略，直至迭代結束。

4 改進遺傳算法結構

改進遺傳算法的流程圖如圖4 所示，基本流程如下：

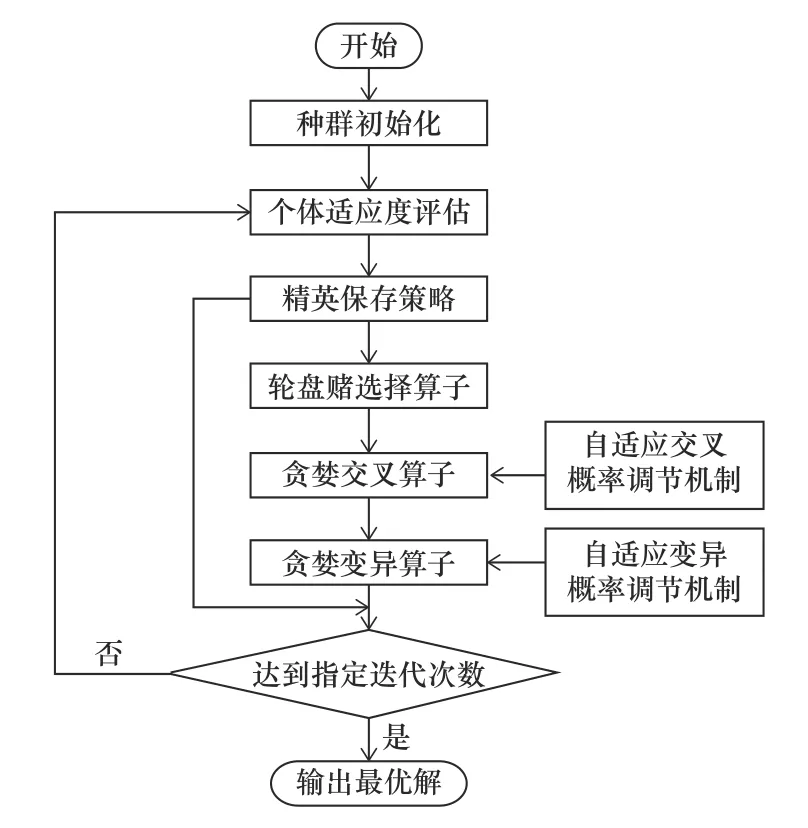
圖4 改進遺傳算法流程圖

（1）生成初始種群。

（2）計算種群各個個體的適應度值。

（3）通過精英保存策略，復制適應度值最大的個體直接進入子代，其余個體繼續進行選擇、交叉和變異操作。

（4）判斷是否達到最大迭代次數，若是，輸出最優解，若否，則返回過程2，計算種群中各個個體的適應度值，用上一輪過程3 復制的最優個體替換這一輪父代中的最差個體，繼續下面的迭代過程。

5 實驗研究

5.1 仿真實驗

設計一個參數曲面作為本次仿真實驗的自由曲面，如圖5 所示。在該曲面上隨機生成100 個點作為路徑測點，用Matlab2018a 編寫算法程序，初始種群數為250，自適應交叉概率為Pci，自適應變異概率為Pmi，代溝GGAP=0.9，最大迭代次數傳統遺傳算法和改進遺傳算法分別是1 200 和500 代。分別用傳統遺傳算法和改進遺傳算法對這100 個測點求解最優路徑，優化軌跡和優化過程如圖6 所示，優化的路徑長度和時間如表2 所示。

圖5 參數曲面

圖6 優化軌跡與優化過程

從圖6a 與b，c 與d 的比較中可以看出，相比于改進的遺傳算法，傳統的遺傳算法生成的最優路徑拐角比較多，且優化代數比改進的遺傳算法高很多，通過表2 可以得出，傳統的遺傳算法出現了過早收斂現象，而且工作效率遠不及改進的遺傳算法，在路徑長度方面改進的遺傳算法比傳統的遺傳算法路徑長度縮短6.8%，在程序耗時方面改進的遺傳算法比傳統的遺傳算法時間縮短了75%。

5.2 實際檢測實驗

參數曲面檢測實驗在意大利COORD3 三坐標測量機下進行，選擇測球直徑為3 mm，定位和回退距離為5 mm，觸測和回退速度為0.55 mm/s，移動速度為10 mm/s，分別對用傳統遺傳算法和改進遺傳算法優化后的100 個測點路徑進行檢測，檢測過程如圖7 所示，并對整個檢測過程計時，實驗結果如表2 所示。

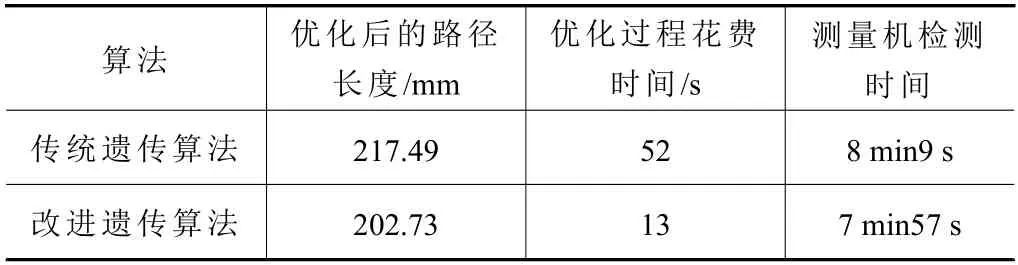
表2 實驗數據

圖7 曲面零件的三坐標檢測

從表2 可以得出，用改進遺傳算法求得的最優路徑檢測時間比傳統遺傳算法的減少了12 s，測量效率提高了2.45%，這可以很好地提高大批量零件檢測的效率，對大批量零件檢測具有重要的意義。

6 結語

在自由曲面測點測量路徑優化方面，改進的遺傳算法無論是在尋求最優路徑的長度方面還是程序的耗時方面都比傳統遺傳算法好很多，改進的遺傳算法不僅找到了更優的測點測量路徑，而且大大提高了求解效率，實驗結果表明改進的遺傳算法能夠更高效且優質的完成自由曲面測量路徑優化。