多材料點陣結構的熱可編程力學行為*
楊 航,馬 力
(哈爾濱工業大學 復合材料與結構研究所,哈爾濱 150001)
引言
傳統點陣結構通過合理的微結構設計獲得了輕量化、高比剛度、高比強度,以及彈性、韌性增強等優異的力學性能,實現了緩沖吸能、隔熱和振動控制等功能應用[1-9].然而傳統的點陣結構一旦制備完成,其預先設定的力學性能以及其他功能通常在使用壽命內保持不變,這制約了點陣結構對不斷變化的環境和工作條件的適應與調節能力.設計和制造具有環境適應特性的智能點陣結構,可編程地感知和響應外界變化(例如光強、壓強、溶液、溫度、電磁場、電化學激勵),并在時間和空間上進行形狀重構、模式轉換和性能調控,仍然是人造材料研究領域一個重要的科學挑戰[10].
形狀記憶聚合物和合金是應用最廣泛的智能材料,能夠承受較大的可編程變形,可以通過溫度控制恢復原始形狀.這種形狀記憶效應被用來調控點陣結構的彈性模量、Poisson 比和帶隙[11-14].Deng 等通過溫度控制液態金屬的固液兩相轉變,實現了由其填充的空芯彈性點陣結構的等效形狀記憶效應[15].然而,這種液態金屬填充的彈性體和大部分的形狀記憶聚合物只具有單向的形狀記憶效應,需要通過訓練實現可逆的構型轉變.雖然液晶彈性體在溫度控制下可在向列相和各向同性相之間可逆轉變,表現為材料的收縮或膨脹變形,但是其制造工藝復雜,承載能力較差[16-17].
另一方面,可以利用磁場對結構材料的變形進行編程.Jackson 等在空管聚合物點陣結構中填充磁流變懸浮液,通過磁場控制實現結構快速的大尺寸形狀重構以及剛度變化[18].但是這類填充結構也存在制備困難、結構復雜、對缺陷敏感等缺點.向聚合物、彈性體、剛性氮化硅膜和水凝膠等基體材料中添加含有磁性的顆粒或納米線,可以更方便地通過磁場進行遠程控制,由其制備的結構表現出極大的可重構性[19-21].然而這種磁控材料缺少形狀鎖定機制,其變形需要恒定的外磁場來維持.為了達到鎖定磁控材料臨時形狀的目的,Ze 等采用向形狀記憶聚合物里添加磁性顆粒的方法,用形狀記憶聚合物的熱塑性來實現結構多模態、多步的變形和重構[22].但是這種方法制造過程復雜,需要向形狀記憶聚合物基體里混合兩種類型的磁性顆粒,一種用于感應加熱,另一種用于驅動材料變形.
能響應多個物理場激勵的智能材料可以提高結構的可控性和靈活性.如由光活性水凝膠和鐵磁性納米線組成的混合材料制成的結構,可以在光和磁場作用下實現快速和可編程的變形[23].由堆疊石墨烯和聚乙烯組成的雙層膜可以通過加熱誘導變形,由其制備的結構可以在紅外照射下實現滾動運動[24].此外,學者們也提出了其他智能材料和結構的激勵-響應機制.Cui 等通過復雜的三維微結構設計,獲得了具有任意壓電系數的壓電超材料,通過施加應力,可以選擇性地抑制、反轉或增強由其產生的電壓響應[25].氣動控制的結構和軟機器人可以實現多種可編程運動和功能應用[26-28].Xia 等和Dehghany 等以電化學和光化學反應為驅動,實現了微點陣結構和凝膠材料的形狀重構[29-30].Li 等通過向點陣結構局部滴入不同溶液,利用相鄰胞壁的毛細力來改變結構的拓撲構型[31].Liu 等和Zhang 等用兩種具有不同剛度和溶脹特性的雙材料制備的多孔結構,在水化作用下表現出負溶脹特性[32-33].
近年來,隨著多材料3D 和4D 打印技術的不斷進步,已經可以制造性能差別很大的、多種材料組成的復雜結構[34-38].通過合理選擇組分材料、設計材料空間分布,多材料點陣結構表現出隨環境條件變化的響應特性.例如,研究人員使用具有不同熱膨脹系數的雙材料,設計并制備了具有可調熱膨脹系數的點陣結構[39-45].Janbaz 等通過將超彈性和黏彈性特性不同的材料組合成雙材料梁,使點陣結構具有應變率相關的力學性能[46].利用非晶態聚合物和彈性體在工作溫度下的剛度反轉效應(即彈性體的模量相對較低,幾乎與溫度無關,而由于玻璃化轉變,非晶態聚合物的模量隨著溫度升高,從遠高于彈性體的模量降低到低于彈性體的模量),Che 等和Yuan 等提出了熱力控制跳變序列和變形模式可轉換的點陣結構[47-48].基于這種剛度反轉效應以及形狀記憶聚合物的形狀記憶效應,Song 等通過在第一個熱循環中進行兩種材料的預應力組裝和第二個熱循環中的拆卸,實現了結構多模態的形狀重構[49-50].基于多材料4D 打印技術,Jeong 等制備了熱力控制的大變形、快速反應的旋轉多穩態結構[51].Zhao 等和Mueller 等調整由兩種具有不同玻璃化轉變溫度的聚合物材料組成的點陣結構的材料分布,通過溫度變化實現了對點陣結構剛度、Poisson 比和變形模式的調控[52-53].
針對目前智能材料和結構激勵-響應機制復雜、制備困難等缺點,本文采用具有不同玻璃化轉變溫度和溫度依賴性的多種聚合物材料,結合多材料3D 打印技術對材料的空間分布進行合理設計,提出了一類具有熱可編程力學響應能力的多材料點陣結構,并研究了其力學行為.以雙V 結構和雙U 結構為例,通過溫度變化實現對多材料點陣結構彈性常數、壓潰響應和結構穩定性的調控,使多材料點陣結構表現出極大的熱變形、超彈性和形狀記憶效應.
1 熱可調結構彈性常數和壓潰響應
傳統的負Poisson 比結構作為機械超材料的一種,其反常的拉脹行為依賴于其微結構的幾何設計,與組分材料無關.所以傳統的負Poisson 比結構一旦制備完成,其力學性能通常在使用壽命內保持不變.這制約了負Poisson 比結構對不斷變化的環境和工作條件的調節能力.以雙V 內凹結構為例[54-60],單材料雙V 內凹結構的Poisson 比由其幾何參數決定,與構成材料的性能無關,如圖1所示.若使用兩種材料改進雙V 內凹結構設計(如圖1(a)所示),則該結構的Poisson 比由兩種材料的相對剛度和幾何參數共同決定.此時,當兩種材料的剛度對溫度的依賴性不同時,則可以通過溫度變化調整兩種材料的相對剛度,進而實現對雙V 內凹結構Poisson 比的調控和編程.
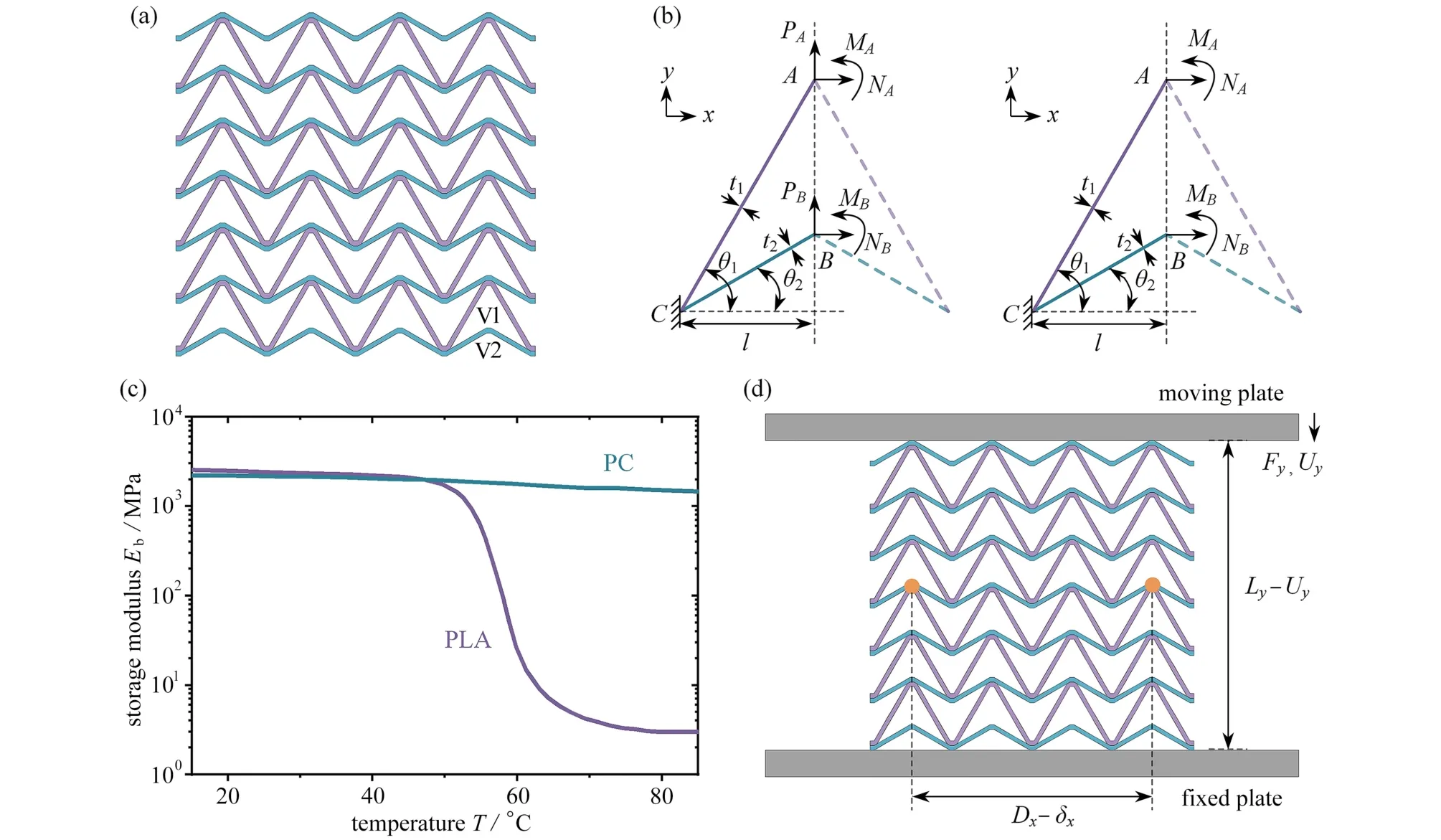
圖1 雙材料雙V 內凹結構:(a)雙材料雙V 內凹結構示意圖;(b)沿y 和x 方向分別加載時的邊界條件;(c)PLA 和PC 材料的儲能模量與溫度的關系;(d)準靜態單軸壓縮示意圖Fig.1 Bimaterial concave double-V structures:(a)schematic diagram of bimaterial concave double-V structures;(b)boundary conditions for loads along y and x directions;(c)storage modulus Eb vs.temperature T for PLA and PC;(d)schematic diagram of quasi-static uniaxial compression
如圖1(a)所示,雙V 內凹結構由交替堆疊的波紋構件V1 和V2 組成.圖中紫色標記部分為V1,彈性模量為E1,密度為 ρ1,面內厚度為t1;藍色標記部分為V2,彈性模量為E2,密度為 ρ2,面內厚度為t2.θ1和 θ2分別為V1 和V2與x軸的傾斜角,且θ1>θ2>0.此外雙V 結構單元的水平投影長度為2l,面外厚度為b.雙V 內凹結構的密度和孔隙率分別為
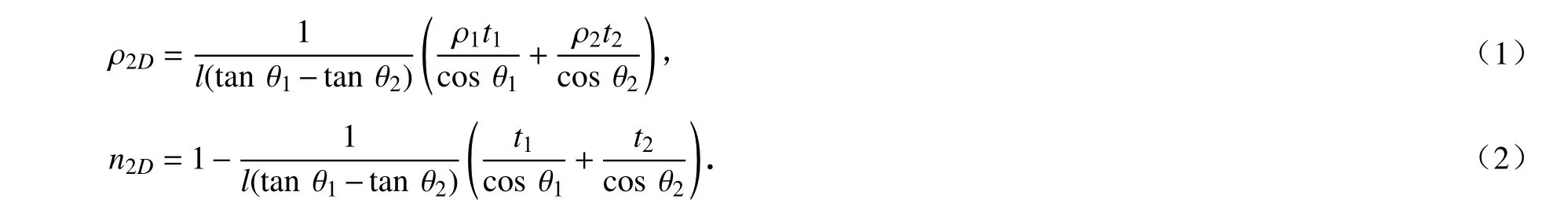
由上述公式可知,雙V 內凹結構的密度隨面內厚度和組分材料密度的增加而線性增加,而孔隙率僅由幾何參數決定.
為了得到雙V 結構的等效彈性常數,本文選取的代表性體積單元如圖1(b)所示,并做如下假設:1)結構桿件的變形均為小變形;2)結構的桿件均為細長桿,忽略剪切以及其他變形,僅考慮軸向和彎曲變形;3)結構桿件間的連接為剛性連接,且在變形過程中角度保持不變;4)雙V 結構在x和y方向上無限延伸,不考慮結構尺寸和邊界效應.



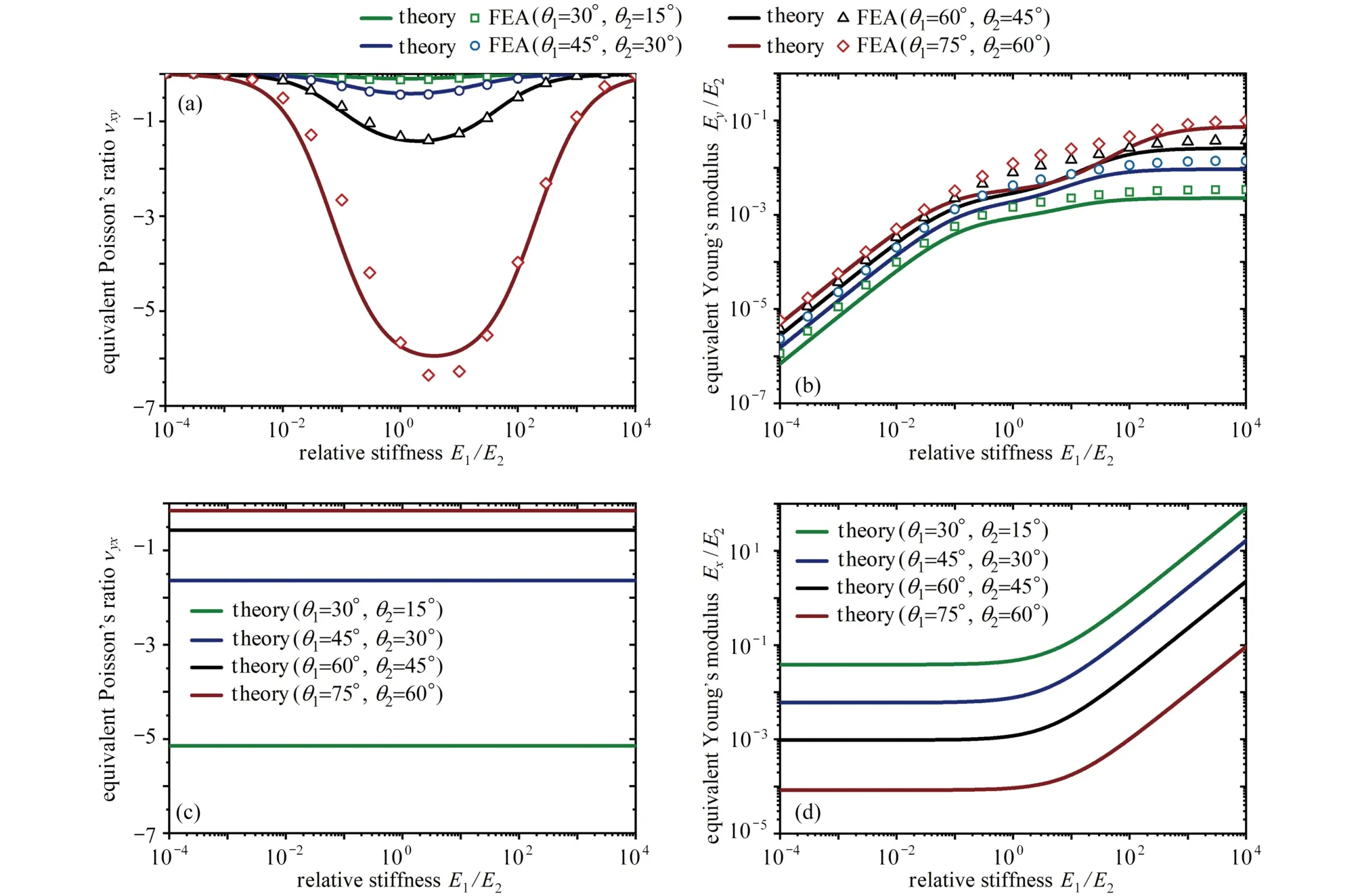
圖2 組分材料相對剛度E1/E2對雙材料雙V 內凹結構彈性常數的影響:(a)Poisson 比ν xy與相對剛度E1/E2的函數關系;(b)彈性模量Ey/E2與相對剛度E1/E2的函數關系;(c)Poisson 比ν yx與相對剛度E1/E2的函數關系;(d)彈性模量Ex/E2與相對剛度E1/E2的函數關系Fig.2 The influence of relative stiffness E1/E2 of the constituent materials on elastic constants of bimaterial double-V structures:(a)equivalent Poisson’s ratio νxy as functions of relative stiffness E1/E2;(b)relative Young’s modulus Ey/E2 as functions of relative stiffness E1/E2;(c)equivalent Poisson’s ratio ν yx as functions of relative stiffness E1/E2;(d)relative Young’s modulus Ex/E2 as functions of relative stiffness E1/E2
通過上述分析可知,通過調整V1 和V2 桿件組分材料的相對剛度E1/E2,可以實現對雙V 結構Poisson 比νxy和彈性模量Ey的調控.上述理論推導中,選擇溫度T為外部環境變量,即E1和E2為溫度T的函數,則可以通過控制溫度變化調整相對剛度E1/E2進而實現對雙V 結構Poisson 比和彈性模量的調控和編程.本文選用對溫度變化敏感的聚乳酸(polylactic acid,PLA)材料和對溫度變化不敏感的聚碳酸酯(polycarbonate,PC)材料演示這一設計效果.通過動態熱機械分析(dynamic mechanical analysis,DMA)測試得到的PLA 材料和PC 材料的儲能模量與溫度的關系如圖1(c)所示.在室溫條件下(即T=20 °C),EPC=2 207 MPa,EPLA=2 517 MPa,這兩種材料表現出幾乎相同的儲能模量.當溫度升高到T=80 °C 時,對溫度變化敏感的PLA 材料的儲能模量大幅降低至EPLA=3 MPa,而對溫度變化不敏感的PC 材料的儲能模量輕微降低至EPC=1 490 MPa,導致兩種材料的儲能模量相差將近三個數量級.采用這兩種材料3D 打印制備了雙V 型結構,其中V1 部分使用PLA 材料,V2 部分使用PC 材料.制備的雙V 內凹結構試件的幾何尺寸為:θ1=60°,θ2=30°,t1=t2=1.5 mm,l=15 mm,b=30 mm.
對制備的試件進行了壓縮測試,試驗設備為帶環境溫箱的萬能試驗機(Instron 5569).試驗過程中,載荷加載速度為0.5 mm/min,溫箱內溫度恒定,我們利用激光引伸計記錄雙V 結構橫向距離變化,如圖1(d)所示.利用有限元分析軟件ABAQUS 模擬了溫度變化對雙材料雙V 結構Poisson 比 νxy和彈性模量Ey的影響.計算中采用平面應變模型,用CPE4 單元對所建立的有限元模型進行網格劃分,通過網格收斂性研究,確定網格尺寸為0.3 mm.分析過程采用靜態分析步(static general),采用通用接觸,定義摩擦因數為0.3,法向采用硬接觸防止單元互相穿透.
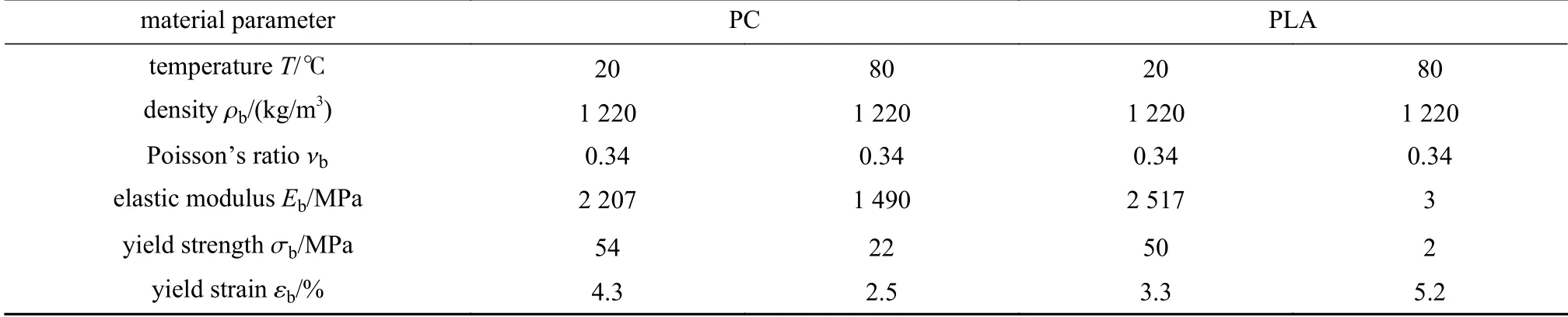
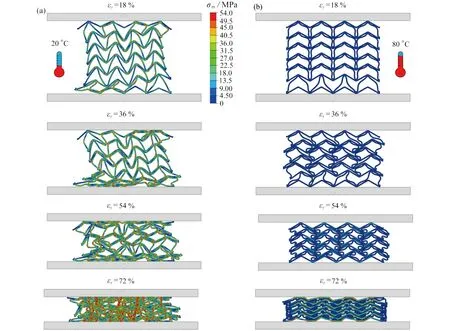
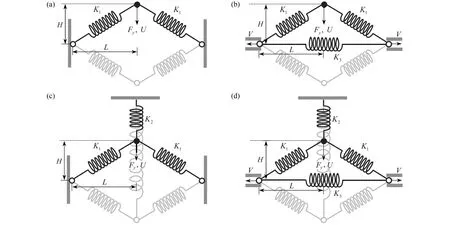
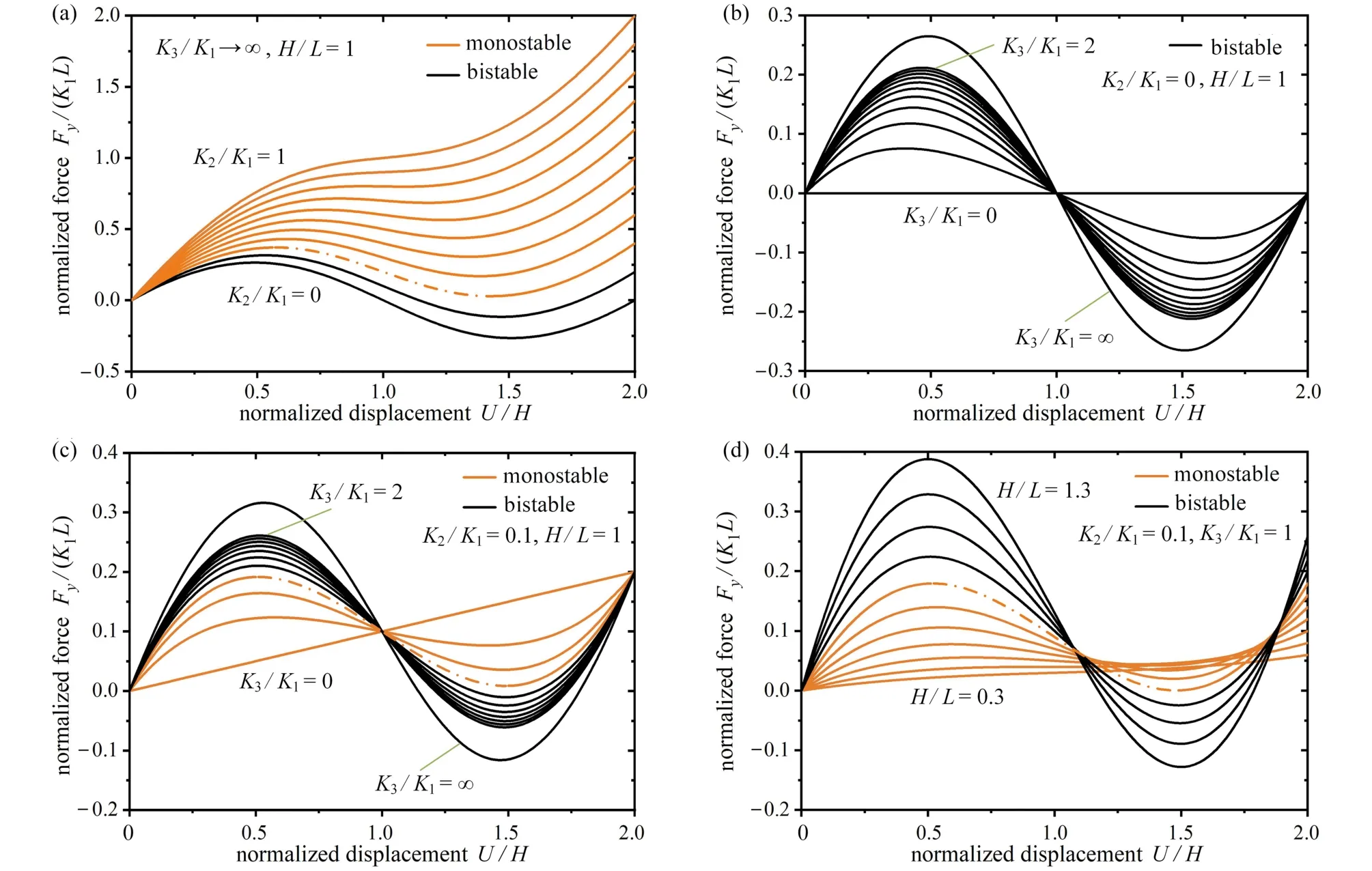
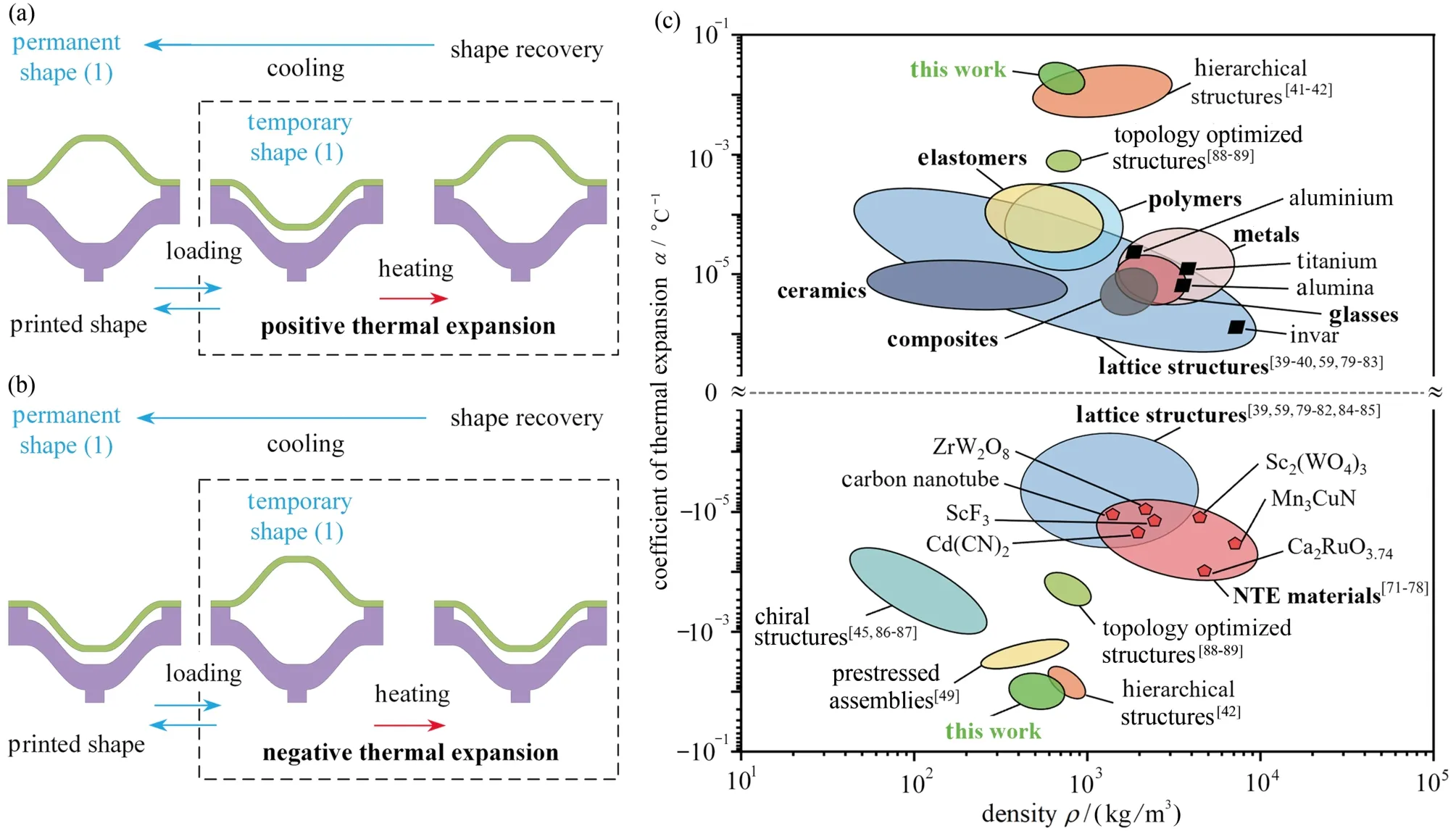
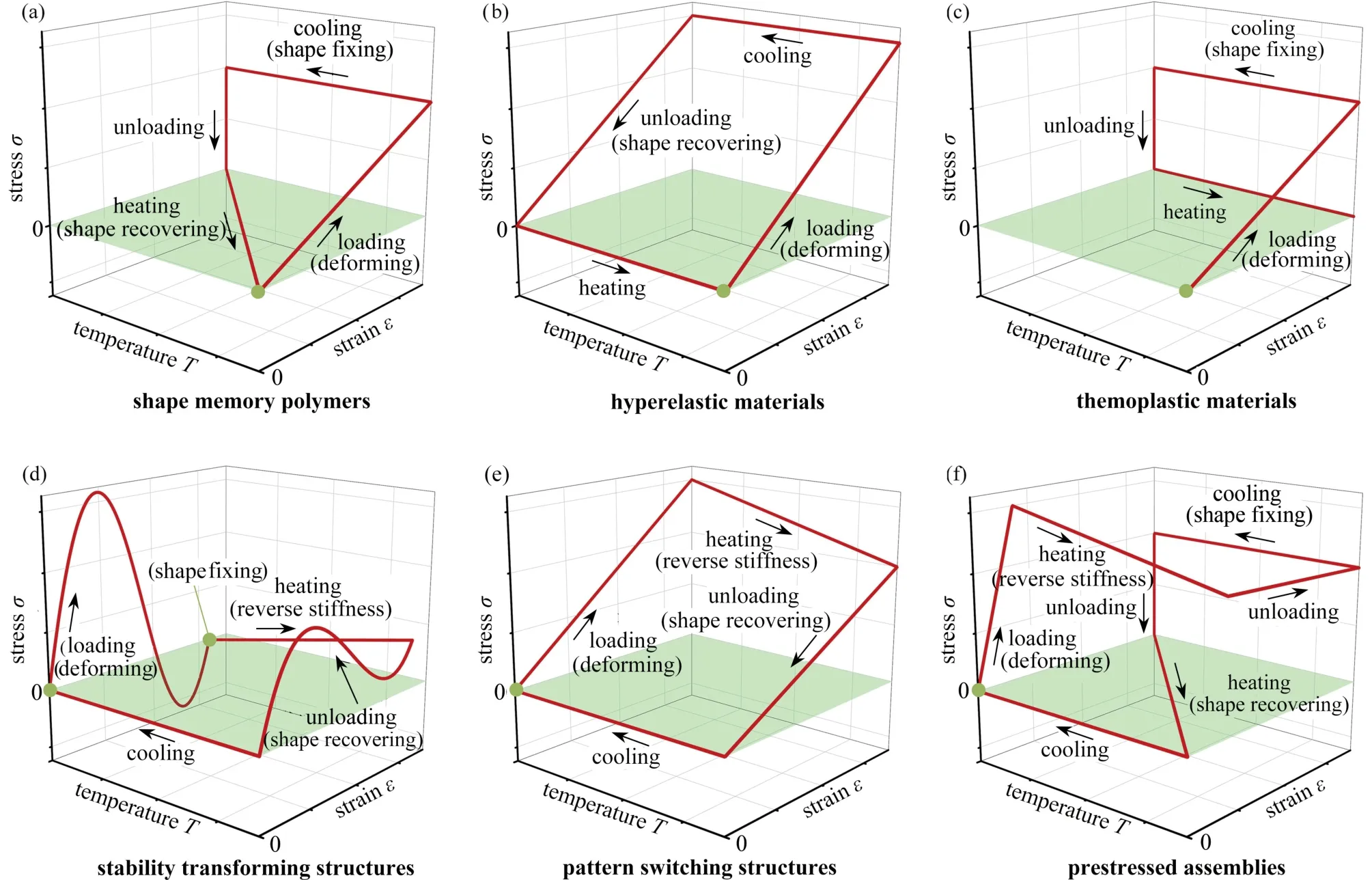
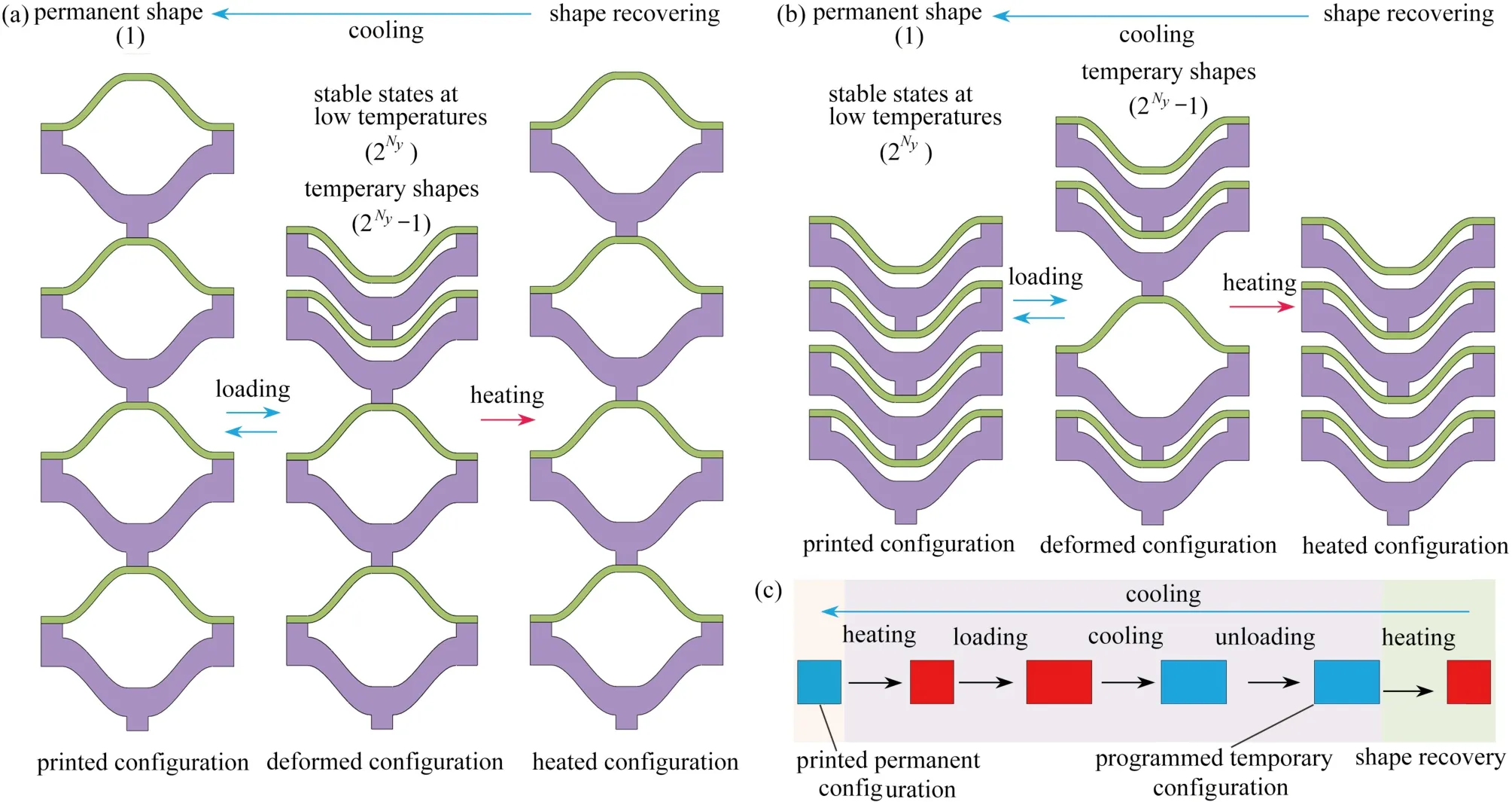
圖3 給出了溫度變化對雙材料雙V 內凹結構彈性常數的影響,雙材料雙V 內凹結構的Poisson 比 νxy和彈性模量Ey的理論、模擬和實驗的結果對比分別如圖3(c)和3(d)所示.當溫度較低(T<50 °C)或較高(T>70 °C)時,組分材料PLA 和PC 的剛度變化很小,雙材料雙V 結構Poisson 比 νxy的值比較穩定;在50 °C 圖3 溫度變化對雙材料雙V 內凹結構彈性常數的影響:(a)低溫時雙V 結構在y 方向受壓時的橫向變形;(b)高溫時雙V 結構在y 方向受壓時的橫向變形;(c)不同溫度下ν xy的理論、模擬和實驗結果對比;(d)不同溫度下 Ey的理論、模擬和實驗結果對比Fig.3 The influences of temperatures on elastic constants of bimaterial double-V structures:(a)simulated lateral deformation for y-direction load at low temperatures;(b)simulated lateral deformation for y-direction load at high temperatures;(c)theoretical,numerical and experimental results of Poisson’s ratio ν xy as functions of temperature T;(d)theoretical,numerical and experimental results of Young’s modulus Ey as functions of temperature T 為了進一步說明通過溫度變化調控雙材料雙V 內凹結構的力學性能,采用數值模擬研究了其在不同溫度下的壓潰行為.在室溫(T=20 °C)和高溫(T=80 °C)環境下的軸向壓潰模擬過程中,有限元模型的幾何參數和結構與實驗樣品一致,分析過程使用顯式動態算法(dynamic explicit),采用具有溫度相關特性的線彈性理想塑性材料模型,最小步長為1 × 10?7s?1,線性和二次黏度系數分別為0.06 和1.2.數值模擬中兩種組分材料的材料參數如表1所示. 表1 有限元分析中組分材料的性能參數Table 1 Mechanical properties of constituent materials used in the finite element analysis 不同溫度下雙材料雙V 結構準靜態壓潰過程的數值模擬結果如圖4所示.雙V 結構在壓縮載荷作用下,V1 桿件承受彎矩和軸向壓力,而V2 桿件承受彎矩和軸向拉力.常溫下,PLA 和PC 材料的彈性模量、屈服應力和屈服應變差別很小,因此雙材料雙V 內凹結構的壓潰變形模式與單一材料雙V 結構的變形模式一致,先橫向向內收縮再橫向向外擴張,如圖4(a)所示.然而在高溫下,PLA 材料的彈性模量迅速降低大約三個數量級,屈服強度降低大約一個數量級,而PC 材料的彈性模量和屈服強度只降低到大約原來的一半.因此,雙材料雙V 結構在高溫下表現為V1 桿件的壓曲變形,在較大的應變下依然保持零Poisson 比,整體變形規則有序,如圖4(b)所示.由于負Poisson 比結構在受壓時的質量集中效應,雙材料雙V 結構在常溫下的應力-應變曲線沒有明顯的平臺應力階段,應力水平隨名義應變的增加逐漸提升.而在高溫下,雙材料雙V 結構在較大的應變下依然保持零Poisson 比,V1 桿件的壓曲失穩變形使得應力-應變曲線抖動劇烈,在V1 桿件壓至與V2 桿件接觸后,再繼續加載導致應力水平迅速提升,如圖5(a)和5(b)所示. 圖4 溫度變化對雙材料雙V 結構變形模式的影響:(a)低溫時雙V 結構在y 方向的壓潰過程;(b)高溫時雙V 結構在y 方向的壓潰過程Fig.4 The influences of temperatures on deformation modes of bimaterial double-V structures:(a)simulated crushing process for y-direction load at a low temperature;(b)simulated crushing process for y-direction load at a high temperature 圖5 溫度變化對雙材料雙V 結構應力-應變響應的影響:(a)低溫時雙V 結構在y 方向壓潰時的應力-應變曲線;(b)高溫時雙V 結構在y 方向壓潰時的應力-應變曲線Fig.5 The influence of temperature on stress-strain response of bimaterial double-V structures:(a)numerical results of stress-strain curve for y-direction load at low temperature;(b)numerical results of stress-strain curve for y-direction load at high temperature 基于彈性跳變機制的雙、多穩態結構具有形狀重構功能,也是機械超材料研究領域的熱點.壓曲梁和原曲梁是研究最廣泛的跳變單元,傳統的單材料雙、多穩態結構采用較厚的支撐部分為跳變部分提供兩端的約束,導致單材料多穩態結構的材料利用率很低.而且單材料多穩態結構的形狀重構需要通過施加外部載荷實現,不具有智能響應機制,如圖6所示.以雙U 多穩態結構為例[61-70],單材料雙U 結構的雙、多穩態機制由彈性跳變部分和支撐部分的幾何參數決定.而如圖6(a)所示,雙材料雙U 結構的彈性跳變部分由另一種材料制成的支撐部分提供兩端的約束,其雙、多穩態機制由兩種材料的相對剛度和幾何參數共同決定.因此,和雙材料雙V 結構類似,當兩種材料的剛度對溫度有不同的依賴性時,就可以通過溫度變化控制兩種材料的相對剛度,進而實現對雙材料雙U 結構穩定性的調控和編程. 如圖6(a)所示,雙U 結構的單元由構件U3 和U4 組成.圖中綠色標記部分為U3,彈性模量為E3,密度為ρ3,紫色標記部分為U4,彈性模量為E4,密度為 ρ4.幾何參數如下:U3 跳變曲梁中心線的垂直投影高度和水平投影長度分別為h和l/2,面內厚度為t3;U4 支撐梁面內厚度為t4,連接平臺的寬度為c,厚度為a.三角函數y=h/2×[1?cos(2πx/l)]在區域[?l/2,0]內的函數曲線作為原曲梁U3 中心線的曲線形式,面外厚度為b. 之前的研究表明[61-70],當彈性跳變梁U3 兩端被完全約束時,通過合理地調整其幾何參數t3/l和h/l,在豎直載荷Fy作用下,彈性梁U3 可以跳變到第二個穩態構型,此時跳變曲梁中心線的垂直投影高度為h'(h' 圖6 雙材料雙U 跳變結構:(a)雙材料雙U 結構及單元幾何參數示意圖;(b)PLA 和TPU 材料的儲能模量與溫度的關系;(c)單穩態和雙穩態單元的力-位移曲線示意圖;(d)單穩態和雙穩態單元的勢能-位移曲線示意圖Fig.6 Bimaterial double-U snapping structures:(a)schematic diagram of bimaterial double-U structures and geometric parameters of the unit cell;(b)storage modulus Eb vs.temperature T for PLA and TPU;(c)force-displacement curves of the monostable and bistable unit cells;(d)potential energydisplacement curves of the monostable and bistable unit cells 為了更簡潔地解釋支撐梁和跳變梁相對剛度E4/E3對雙U 結構穩定性的影響,本文研究了與其具有相同跳變機制的von Mises 桁架模型[61-70].圖7 給出了von Mises 桁架模型的系統穩定性分析.最簡單的von Mises 桁架如圖7(a)所示,兩個具有剛度K1和原始長度S0的線彈性彈簧,其端部為銷連接,在其自然狀態下與水平面成非零角度傾斜.為了給系統提供慣性,在彈簧相交的地方放置一個點質量M,并限制點質量僅在垂直方向上移動.最簡單的von Mises 桁架具有完全對稱的雙穩態,因為高亮顯示和輕度著色的平衡態相對于水平軸具有對稱性.這種完全對稱的雙穩態機制與壓曲梁具有相同的力學表現.當豎直外力Fy作用于點質量時,圖7(a)所述保守系統的總勢能由彈性勢能Et和外力勢能W組成: 系統的力和位移的關系為 然而,將一定剛度的附加線彈性彈簧K2垂直連接到點質量上時,輕度陰影區域不再是穩定平衡位置,如圖7(c)所示.這樣,取決于相對剛度K2/K1和無量綱幾何參數H/L,三個相連的線彈性彈簧具有單穩態或者不對稱雙穩態.該系統與斜直梁、原曲梁和軸對稱殼體等具有相同的力學表現,可以用來解釋其跳變機制.圖7(c)所述系統的彈性勢能由下式給出: 圖7 Von Mises 桁架模型的系統穩定性分析:(a)兩端完全約束的對稱雙穩態系統;(b)兩端不完全約束的對稱雙穩態系統;(c)兩端完全約束并加上豎直彈簧的非對稱雙穩態或單穩態系統;(d)兩端不完全約束并加上豎直彈簧的非對稱雙穩態或單穩態系統Fig.7 System stability analysis of von Mises truss models:(a)the symmetric bistable system with complete constraints at both ends;(b)the symmetric bistable system with incomplete constraints at both ends;(c)the asymmetric bistable or monostable system with a vertical spring and complete constraints at both ends;(d)the asymmetric bistable or monostable system with a vertical spring and incomplete constraints at both ends 系統的力和位移的關系為 在周期性的整體結構中,跳變部分末端的約束由支撐段提供,不能形成完全固定的邊界條件.因此,需要使用如圖7(b)和7(d)所示的具有剛度K3的水平線彈性彈簧,來替換如圖7(a)和7(c)所示橫向完全約束的邊界,并模擬結構的橫向擴張和收縮阻力.圖7(b)所述系統的彈性勢能由下式給出: 圖7(d)所述系統的彈性勢能由下式給出: 圖7(b)和7(d)所示系統的力和位移的關系可以通過求解下列方程給出: 通過對上述桁架系統的分析,整理總結von Mises 桁架模型的力-位移響應規律如圖8所示.圖中實線-虛線-實線的橙色線為單穩態和雙穩態的分界線,該橙色線虛線部分表示負增量剛度階段,實線部分表示正增量剛度階段.豎直彈簧K2的作用體現在:當K2/K1=0時,桁架相對于水平軸對稱,為對稱雙穩態系統,因此其力-位移曲線相對于零力點(U/H=1,0)中心對稱,零力點(U/H=1,0)出現在當兩個彈簧都水平的時刻,如圖8(b)所示;當K2/K1>0時,豎直彈簧K2在變形過程中存儲了額外的彈性變形能,因此系統的對稱性被破壞,零力點被轉移到具有更高位移的位置.如圖8(a)所示,隨著K2/K1逐漸增加,曲線逐漸提升,并在大于某一特定值時與零力水平線(Fy=0)不再相交,桁架從雙穩態系統變為單穩態系統.隨著K2/K1進一步增加,單穩態系統的力-位移曲線從正增量剛度-負增量剛度-正增量剛度的非單調函數變為正增量剛度的單調函數,而雙穩態系統的力-位移曲線始終保持從正增量剛度-負增量剛度-正增量剛度的非單調函數.水平彈簧K3的作用體現在:當K2/K1=0時,對稱雙穩態系統力-位移曲線的最大值隨著K3/K1的增加而不斷增加,但是增幅越來越小,如圖8(b)所示,其中K3/K1→∞對應橫向完全約束時的極限曲線;當K2/K1>0時,雙穩態系統力-位移曲線的最大值隨著K3/K1的增加而不斷增加,但是增幅越來越小,并在大于某一特定值時與零力水平線不再相交,桁架從不對稱雙穩態系統變為單穩態系統.隨著K3/K1進一步增加,單穩態系統的力-位移曲線從正增量剛度-負增量剛度-正增量剛度的非單調函數變為正增量剛度的單調函數,如圖8(c)所示,其中K3/K1→∞對應橫向完全約束時的極限曲線,并且曲線均相對于非零力點(U/H=1,K2/K1)中心對稱.幾何參數H/L的作用體現在:當K2/K1=0時,對稱雙穩態系統力-位移曲線的最大值隨著H/L增加而不斷增加;當K2/K1>0時,隨著H/L不斷增加,單穩態系統的力-位移曲線從正增量剛度的單調函數變為正增量剛度-負增量剛度-正增量剛度的非單調函數,隨著H/L再次增加,負力(Fy<0)出現,桁架從單穩態系統變為不對稱雙穩態系統.并且非對稱系統的力-位移曲線的最大值的增加速度比最小值的減少速度快,如圖8(d)所示. 圖8 Von Mises 桁架模型的力-位移響應:(a)K3/K1 →∞且H/L=1時,K2/K1 對系統力-位移曲線的影響;(b)K2/K1=0且 H/L=1時,K3/K1對系統力-位移曲線的影響;(c)K2/K1=0.1且 H/L=1時,K3/K1對系統力-位移曲線的影響;(d)K2/K1=0.1且K3/K1=1時,H/L對系統力-位移曲線的影響Fig.8 The force-displacement responses of von Mises truss models:(a)the influence of K2/K1 on the force-displacement curves of the system for K3/K1 →∞and H/L=1;(b)the influence of K3/K1 on the force-displacement curves of the system for K2/K1=0 and H/L=1;(c)the influence of K3/K1 on the force-displacement curves of the system for K2/K1=0.1 and H/L=1;(d)the influence of H/L on the force-displacement curves of the system for K2/K1=0.1 and K3/K1=1 由于雙材料雙U 結構與圖7(d)所示桁架系統的力學行為的機制相同,將t3/l類比于K2/K1,將h/l類比于H/L,將(E4I4)/(E3I3)類比于K3/K1.通過分析圖7(d)所示桁架系統的跳變機制,可以說明如何通過控制支撐梁U4 和跳變梁U3 的相對剛度E4/E3改變雙材料雙U 結構的穩定性.如圖8(c)所示,在保持K2/K1=0.1,H/L=1不變的情況下,當桁架兩端完全固定約束(K3/K1=∞)時,力-位移曲線為正增量剛度-負增量剛度-正增量剛度的非單調函數,有負力出現,為非對稱的雙穩態系統;當橫向彈簧的剛度減小到K3/K1=0.4時,力-位移曲線為正增量剛度-負增量剛度-正增量剛度的非單調函數,沒有負力出現,為非對稱的單穩態系統;當橫向彈簧的剛度減小到K3/K1=0時,力-位移曲線為正增量剛度的單調函數,無負增量剛度階段.通過上述分析可知,通過外部激勵調整組成支撐梁U4 和跳變梁U3 的組分材料的相對剛度E4/E3可以實現對雙U 結構單元穩定性的調控.本文選用對溫度變化敏感的PLA 材料和對溫度變化不敏感的熱塑性聚氨酯(thermoplastic polyurethane,TPU)材料,結合多材料3D 打印技術,通過控制溫度變化調整相對剛度E4/E3進而實現對雙U 結構穩定性的調控和編程. 使用FDM 3D 打印機制備了雙材料雙U 結構,雙U 整體結構的U3 部分使用TPU 材料,U4 部分使用PLA 材料進行打印.制備的雙U 結構試件的幾何尺寸為:h=7 mm,l=18 mm,t3=1.0 mm,t4=4 mm,c=3 mm,a=2 mm,b=30 mm.通過DMA 測試得到的TPU 材料(綠線)和PLA 材料(紫線)儲能模量與溫度的關系如圖6(b)所示.由于室溫下(T=20 °C)兩種材料的儲能模量為ETPU=87 MPa,EPLA=2 517 MPa,跳變梁U3 的兩端幾乎被支撐梁U4 完全約束,使雙U 結構具有雙穩態單元;當升高溫度到T=80 °C 時,兩種材料的儲能模量為ETPU=26 MPa,EPLA=3 MPa,支撐梁U4 無法繼續為跳變梁U3 的兩端提供足夠的橫向約束,使得室溫下的雙穩態單元轉變為高溫下的單穩態單元. 打印的完全展開和完全閉合的兩個雙U 結構在室溫(T=20 °C)下通過外力作用(手動壓縮和拉伸)實現形狀重構,再將變形后的臨時穩定結構加熱(放入T=80 °C 的熱水中)實現形狀恢復,整個恢復過程用時30 s,其實驗過程如圖9(a)和9(b)所示.雙U 結構在加熱恢復過程中會有很大的熱變形:當初始結構的單元是外凸構型時,加熱過程中會出現正的熱膨脹,如圖10(a)所示;相反,當初始結構的單元是內凹構型時,加熱過程中會出現負的熱膨脹,如圖10(b)所示.從常溫(T=20 °C)加熱到高溫(T=80 °C),初始外凸雙U 結構的等效正熱膨脹系數和初始內凹雙U 結構的等效負熱膨脹系數與已知文獻中的材料和結構的實驗結果對比如圖10(c)所示,如天然材料[42,59]、負熱膨脹材料[71-78]、傳統點陣結構[79-85]、手性結構[45,86-87]、拓撲優化結構[88-89]、多級結構[41-42]、預應力裝配體[49].可以看出,雙U 結構比已知文獻中的材料和結構具有更大的正熱膨脹系數(αmax=0.03°C?1)和更小的負熱膨脹系數(αmin=?0.01°C?1). 圖9 雙U 結構的形狀重構和恢復的實驗過程:(a)初始完全展開的雙U 結構的形狀重構和恢復過程;(b)初始完全閉合的雙U 結構的形狀重構和恢復過程Fig.9 Experimental processes of shape reconfiguration and recovery of double-U structures:(a)shape reconfiguration and recovery of initial double-U structure with fully expanded configuration;(b)shape reconfiguration and recovery of initial double-U structure with fully contracted configuration 圖10 雙材料雙U 結構在加熱恢復過程中的熱變形及熱膨脹系數:(a)初始外凸單元加熱恢復過程中的正熱膨脹變形;(b)初始內凹單元加熱恢復過程中的負熱膨脹變形;(c)雙U 結構在加熱恢復過程中的熱膨脹系數與已知文獻中的材料和結構的實驗結果對比Fig.10 Thermal deformations and thermal expansion coefficients of bimaterial double-U structures during heating recovery:(a)the positive thermal expansion of an initial convex unit cell during heating recovery;(b)the negative thermal expansion of an initial concave unit cell during heating recovery;(c)the thermal expansion coefficients of bimaterial double-U structures during heating recovery compared with the experimental results of materials and structures reported previously 為了更好地將本文的雙材料雙U 結構與其他不同材料和結構的熱力學行為進行對比,我們繪制了熱力循環ε-T-σ示意圖.形狀記憶聚合物的ε-T-σ如圖11(a)所示[90-94].高溫下在外載荷作用時形狀記憶聚合物產生變形,維持外載荷不變的情況下冷卻到低溫,形狀記憶聚合物形狀固定,之后卸掉外載荷,其在低溫下保持臨時形狀不變,升溫后形狀記憶聚合物材料在沒有外載荷的情況下逐漸恢復到初始的永久形狀.作為對比,高溫下超彈性材料在外載荷作用下產生變形,維持外載荷不變的情況下冷卻到低溫,之后卸掉外載荷,其在低溫下不能保持臨時形狀不變,卸載后直接回到初始形狀,有彈性恢復沒有形狀固定,其ε-T-σ如圖11(b)所示.而高溫下熱塑性材料在外載荷作用下產生變形,維持外載荷不變的情況下冷卻到低溫,熱塑性材料形狀固定,之后卸掉外載荷,其在低溫下保持臨時形狀不變,升溫后熱塑性材料在沒有外載荷的情況下依舊保持變形后的形狀,不能恢復到初始形狀,有形狀固定沒有形狀恢復,其ε-T-σ如圖11(c)所示.本文通過分析跳變機制,通過溫度控制支撐部分對跳變部分的約束力,在低溫下可以使雙穩態單元在不同穩態構型之間通過外載荷作用進行跳變,通過勢能阱鎖定結構的臨時形狀.在升溫時,由于支撐部分的剛度急劇降低,不能提供維持跳變部分臨時形狀的橫向約束力,使彈性跳變部分變為單穩態自恢復狀態,通過彈性恢復力實現跳變部分的形狀恢復,而支撐部分的變形由形狀記憶聚合物的形狀記憶效應實現形狀恢復,其ε-T-σ如圖11(d)所示.為了進一步說明本文的穩定性轉換雙U 結構的優勢,選取模式轉換結構和預應力裝配體進行對比[48-49].如圖11(e)所示,低溫下模式轉換結構在外載荷作用下發生變形,升溫后,由于兩種材料的剛度反轉效應,變形模式發生轉換.如果卸掉外載荷,結構可以通過彈性材料的彈性恢復力和形狀記憶聚合物的形狀記憶效應實現形狀恢復,降溫回到初始狀態.但是這種結構設計無法提供形狀固定的機制,沒有形狀重構功能.而預應力裝配體需要經過低溫下組裝-升溫變形-降溫形狀固定-拆卸-升溫形狀恢復(形狀記憶聚合物的形狀記憶效應)-降溫一系列非常復雜的熱力過程才能實現形狀重構,如圖11(f)所示. 圖11 不同材料和結構的熱力循環ε-T-σ示意圖:(a)形狀記憶聚合物ε-T-σ示意圖[90-94];(b)超彈性材料ε-T-σ示意圖;(c)熱塑性材料ε-T-σ示意圖;(d)穩定性轉換雙U 結構單元ε-T-σ示意圖;(e)模式切換結構ε-T-σ示意圖[48];(f)預應力裝配體ε-T-σ示意圖[49]Fig.11 The ε-T-σ diagrams of the thermomechanical cycle for different materials and structures:(a)the ε-T-σ diagram of shape memory polymers[90-94];(b)the ε-T-σ diagram of hyperelastic materials;(c)the ε-T-σ diagram of themoplastic materials;(d)the ε-T-σ diagram of the unit cell of stability transforming double-U structures;(e)the ε-T-σ diagram of the pattern switching structures[48];(f)the ε-T-σ diagram of the prestressed assemblies[49] 由Ny個雙穩態單元串聯而成的雙材料雙U 結構如圖12(a)和12(b)所示,每一個結構在常溫下有 2Ny個穩態構型.其中初始構型是其永久形狀,剩下的2Ny?1個穩態構型為臨時形狀,穩態構型在常溫下可以通過力加載任意切換,升溫后均回到初始永久形狀.相比如圖12(c)所示形狀記憶材料,穩定性轉換雙U 結構的形狀重構不需要復雜的編程過程,在極大的應變下依然能恢復到初始形狀,并且能反復循環使用,表現出遠超形狀記憶合金和聚合物的超彈性和形狀記憶效應. 圖12 穩定性轉換雙U 結構的形狀重構和變形恢復機制:(a)初始完全展開的雙U 結構的形狀重構和恢復機制;(b)初始完全閉合的雙U 結構的形狀重構和恢復機制;(c)形狀記憶聚合物的形狀重構和變形恢復機制Fig.12 The shape reconfiguration and recovery mechanism of the stability transforming double-U structures:(a)the shape reconfiguration and recovery mechanism of initial structures with fully expanded configurations;(b)the shape reconfiguration and recovery mechanism of initial structures with fully contracted configurations;(c)the shape reconfiguration and recovery mechanism of shape memory polymers 本文針對目前智能材料和結構激勵-響應機制復雜、制備困難等缺點,采用了具有不同玻璃化轉變溫度和溫度依賴性的多種聚合物材料,結合多材料3D 打印技術對材料的空間分布進行合理設計,提出了一類具有熱可編程力學響應能力的多材料點陣結構,并研究了其力學行為.設計的雙材料雙V 結構可通過溫度變化實現對其等效彈性常數和壓潰響應的調控和編程.雙材料雙U 結構可以通過簡單的熱力控制實現形狀重構和形狀恢復功能,表現出了極大的熱變形、超彈性和形狀記憶效應.本文提出的具有熱可編程力學響應能力的多材料點陣結構的設計、分析和驗證方案可以很容易地擴展到調控點陣結構的其他性能和響應其他環境刺勵,為設計和制造自適應保護裝備、生物醫學設備、航空航天領域的變形結構、柔性電子設備、自組裝結構和可變形軟體機器人等開辟了新途徑.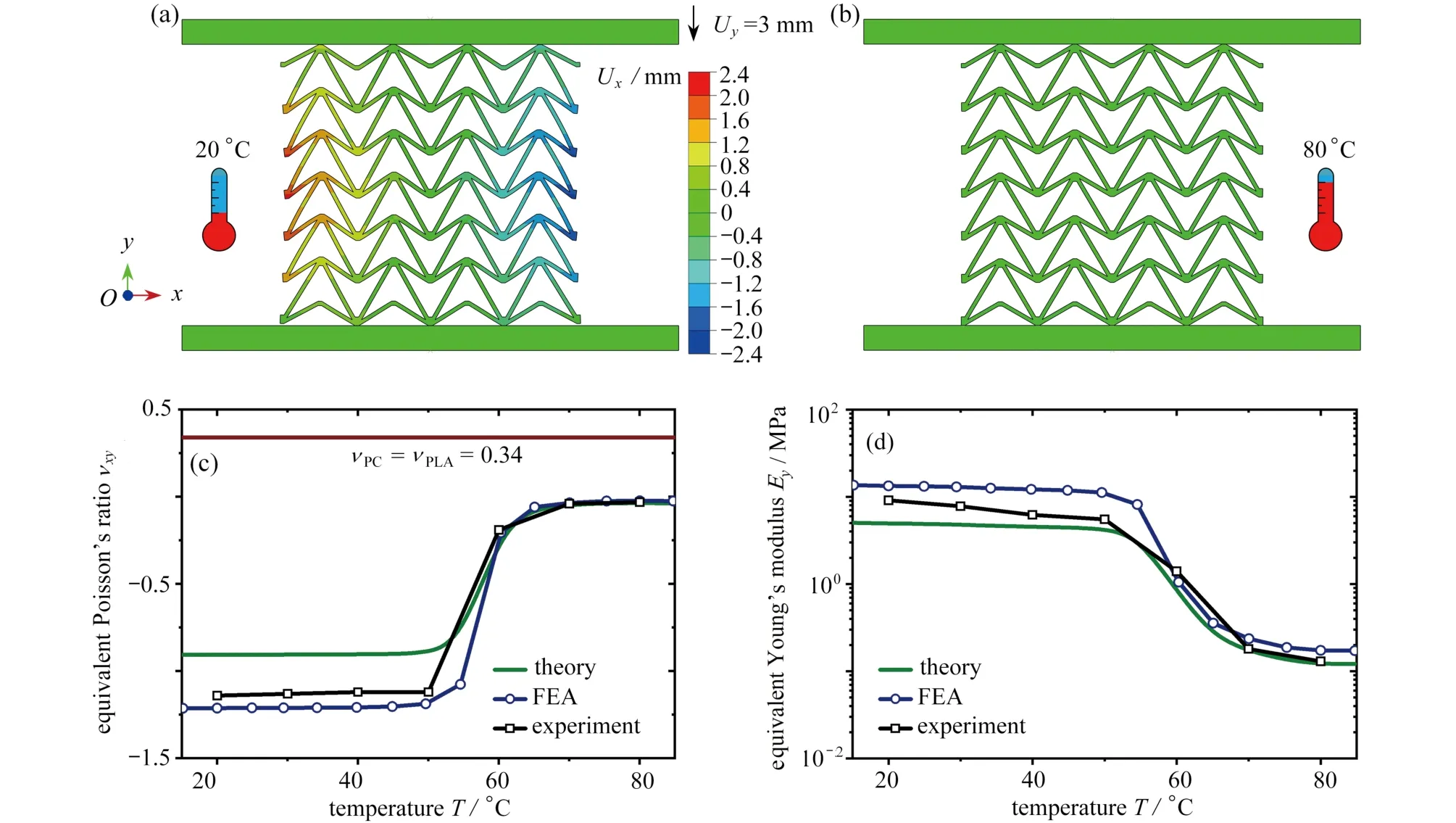
2 熱可調結構穩定性
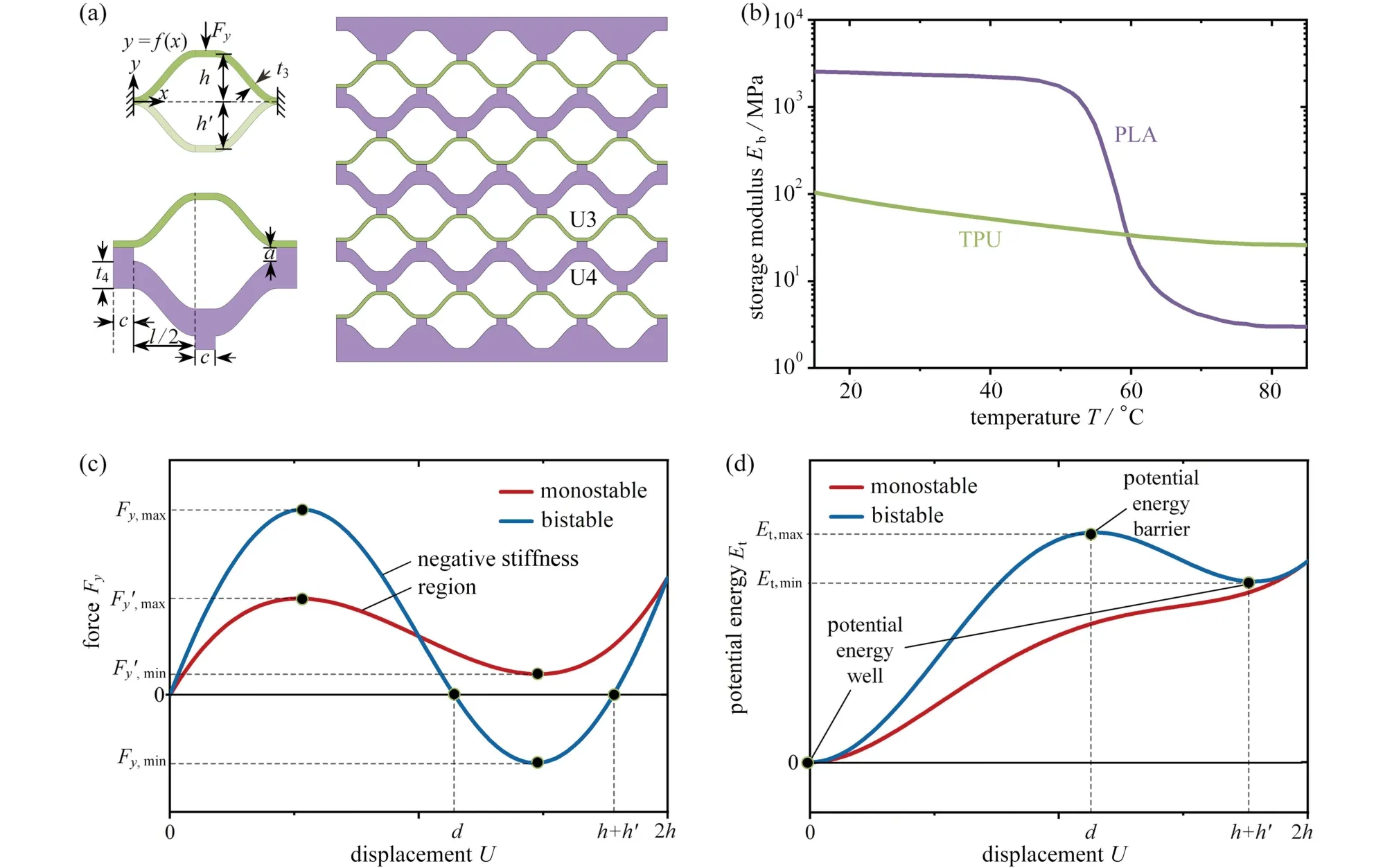
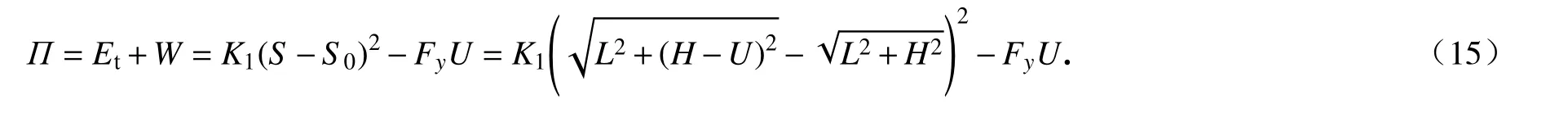

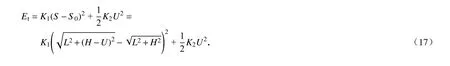
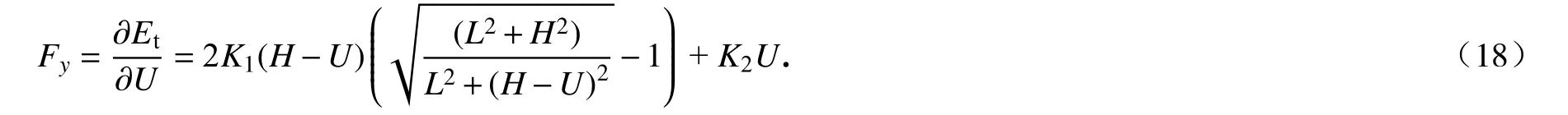
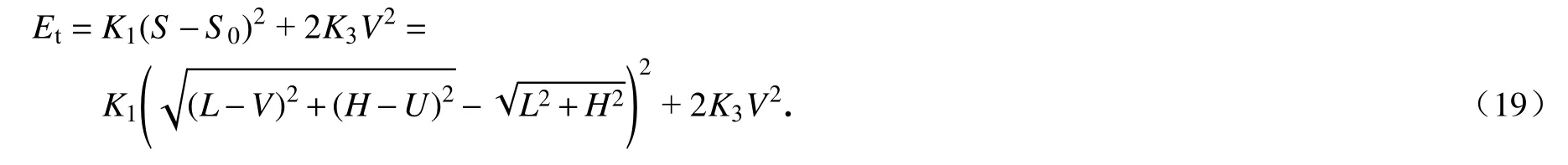
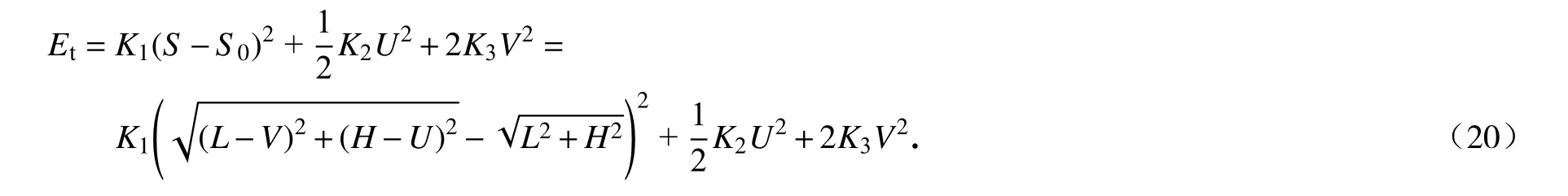


3 結論

