礦井淋水井筒風溫PSO-SVR預測方法

高佳南，吳奉亮，馬 礪，賀雁鵬

(1.西安科技大學 安全科學與工程學院，陜西 西安 710054；2.西安科技大學 西部礦井開采及災害防治教育部重點實驗室，陜西 西安 710054)

0 引 言

隨著礦井開采深度的加大，井下風溫不斷升高，熱害問題日益突出，嚴重制約著深部煤炭資源的安全高效開采[1-2]。為充分掌握井巷風流熱力狀態變化規律，準確評估礦井熱害程度，從而制定科學合理的降溫方案，改善井下高溫作業環境，進而保護工作人員的身心健康，礦井風溫預測研究至關重要[3]。

國內外眾多學者對礦井風溫預測做了大量研究。LOWNDES等構建了巷道氣候預測模型并分析了有關熱力參數[4]；KRASNOSHTEIN等基于拉普拉斯變換確定了圍巖與風流間非穩態換熱的積分表達式[5]；侯祺棕等分析了風溫與風流濕度間變化的相關關系，并建立了將風溫與風流濕度相結合的預測模型[6]；張習軍研究了井下風溫的線性回歸計算式[7]；高建良等通過對飽和空氣含濕量與溫度進行二次曲線擬合來處理巷壁水分蒸發，并解算出風溫及濕度的變化規律[8]；孔松等利用有限差分方法建立了進風井筒及巷道的風溫迭代預測模型[9]。從上述文獻中可以看出，礦井風溫預測方法主要有實驗室模型模擬法、數學分析法、實測回歸統計法等[10-12]。實驗室模型模擬法往往受實驗條件所限，預測精度很難精確[13]。數學分析法是通過傳熱學理論建立熱傳導方程，計算精度相對較高，而實際條件復雜，涉及的熱物性等基礎參數各異且難以獲取，在計算方法上采取了假設簡化，影響風溫預測精度[14]。實測回歸統計法是在現場實測數據基礎上進行回歸預測，解決了應用理論方法求解風溫的困難，但風溫與其他參數之間存在著某種非線性關系，該方法下的風溫預測精度不佳[15-16]。近年來機器學習的智能算法在礦井風溫預測方面有所應用，如BP神經網絡[15，17-18]、支持向量機(SVM)[19]等。BP神經網絡具有優越的非線性處理能力，但其預測精度受學習樣本規模的影響較大，且易出現模型在訓練樣本中擬合效果好，而在測試樣本表現差的過擬合現象，泛化性能較低[20]；SVM是一種基于統計學習理論的機器學習算法，具有嚴格的數學邏輯，能夠較好地解決小型數據樣本、高維度、非線性的問題，學習與泛化能力強，將SVM推廣到回歸問題可得到支持向量回歸SVR[21]，能夠處理井巷風溫與其影響因素之間存在的非線性函數關系。

礦井入風井筒風溫是井下空氣熱計算的重要節點，其風溫關系到整個礦內的熱環境。當井筒有淋水現象時，其風溫的求解涉及到風流與淋水水滴混合流的復雜熱交換，因此，理論計算淋水井筒風溫較為困難[22]。另外，許多學者在井筒風溫預測研究中未考慮淋水的存在[16]，導致預測結果不理想。基于上述分析，文中提出利用支持向量回歸法(SVR)來預測礦井淋水井筒風溫，并利用粒子群算法(PSO)對支持向量回歸參數進行優化，建立參數優化的支持向量回歸模型(PSO-SVR)，以期獲得準確的礦井淋水井筒風溫預測方法。

1 礦井淋水井筒風溫PSO-SVR預測模型

1.1 支持向量回歸SVR

給定訓練樣本集T={(x1，y1)，(x2，y2)，…，(xi，yi)，…，(xn，yn)}，其中xi為輸入特征向量，yi為輸出向量(淋水井筒風溫)，SVR是將低維輸入空間數據通過非線性映射算法φ轉化到高維特征空間φ(x)，進而在特征空間中擬合一個線性回歸函數

f(x)=w·φ(x)+b

(1)

式中w為權向量；b為偏置常數。

對于任意ε>0有|yi-f(x)|≤ε，f(x)為訓練樣本集T的ε-線性回歸，此時認為模型預測值正確，則SVR問題可描述為

(2)

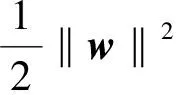
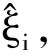
(3)

s.t.yi-f(xi)-b≤ε+ξi

對式(3)做拉格朗日函數得到對偶問題

(4)

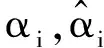
由此可得礦井淋水井筒風溫回歸預測值

(5)

對于礦井淋水井筒風溫預測SVR模型，選擇具有較強泛化性的高斯徑向基核函數[23]，預測模型中懲罰因子C和核函數參數g的選取對預測結果的準確度有著重要影響[24]。當懲罰因子C值選取過大會造成過擬合，致使預測模型的泛化性能降低；若此值太小將加大模型對誤差的容忍程度，容易出現欠擬合現象。核函數參數g太大，會使支持向量間的影響過強，造成算法精度降低；若此值太小，則支持向量間的聯系較松弛，學習機器相對復雜，導致模型泛化性能差。為了提高預測精度，文中采用PSO對SVR預測模型進行參數尋優。

1.2 粒子群優化算法

PSO算法的基本思想是：模擬鳥群根據自身經驗和種群交流來調整搜尋路徑繼而尋找到食物的捕食行為。在PSO算法中，用粒子代表優化問題的解，粒子特征用位置、速度來描述，優化求解首先是在搜索空間中隨機初始化每個粒子的速度和位置，根據粒子的適應度函數值，迭代搜索最優解。每次迭代搜尋時粒子都會根據自身歷史最優位置和粒子種群當前最優位置來更新自身的搜尋速度和位置，最終找到最優解。

假設在D維搜索范圍中有粒子n個，粒子i的位置xi=(xi1，xi2，…，xid)，i=1，2，…，n，速度vi=(vi1，vi2，…，vid)，個體歷史最優位置pbestid=(pi1，pi2，…，pid)，粒子種群當前搜索到的最優位置gbestd=(g1，g2，…，gd)。

按式(6)計算粒子i的第k+1次迭代后速度矢量的第d維分量

(6)

按式(7)計算粒子i的第k+1次迭代后位置矢量的第d維分量

(7)

將訓練樣本的預測結果的均方誤差作為適應度函數，更新種群粒子的速度、位置，確定最優SVR參數(C，g)，建立礦井淋水井筒風溫PSO-SVR預測模型。

1.3 預測結果評價

對于礦井淋水井筒風溫預測回歸模型的預測結果，文中采用平均絕對誤差MAE，平均絕對百分比誤差MAPE，均方誤差MSE等3項統計量對其預測效果進行評價。其中，

平均絕對誤差MAE

(8)

平均絕對百分比誤差MAPE

(9)

均方誤差MSE

(10)

式中f(xi)為預測值，℃；yi為觀測值，℃。

2 PSO-SVR預測模型建立

利用PSO優選SVR的懲罰因子C和核函數參數g，建立井筒風溫PSO-SVR預測模型，其尋優預測過程如圖1所示。主要步驟如下。

1)訓練和測試樣本數據歸一化。將訓練和測試樣本數據按式(11)(12)歸一化在[0，1]區間

(11)

式中xti為特征屬性t的原始輸入數據；min{xti}為特征屬性t的原始輸入數據最小值；max{xti}為特征屬性t的原始輸入數據最大值。

(12)

式中yi為原始輸出數據；min{yi}為原始輸出數據最小值；max{yi}為原始輸出數據最大值。

2)PSO初始化。算法參數的初始化：設定粒子群算法最大進化代數為100，種群數目20，懲罰因子C∈[0.1，100]，核函數參數g∈[0.01，100]，局部搜索能力c1=1.5，全局搜索能力c2=1.7，對訓練樣本進行5折交叉驗證；種群20個粒子的位置和速度初始化。

3)計算每個粒子的適應度。初始化的粒子位置向量(C，g)輸入SVR后建模，將預測結果的均方誤差作為對應粒子的適應度。

4)優選個體適應度。比較20個粒子的適應度，以適應度最小為最優，得到當前群體的最優位置。

5)迭代更新種群適應度，獲得最優SVR參數(C，g)。按照式(6)、式(7)分別更新種群粒子的位置和速度，重復步驟3)4)，更新優選出種群最小適應度，對應粒子的(C，g)為最優位置向量，即最優SVR參數。

6)將訓練樣本輸入SVR，最優SVR參數(C，g)賦值于SVR，建立礦井淋水井筒風溫PSO-SVR預測模型。

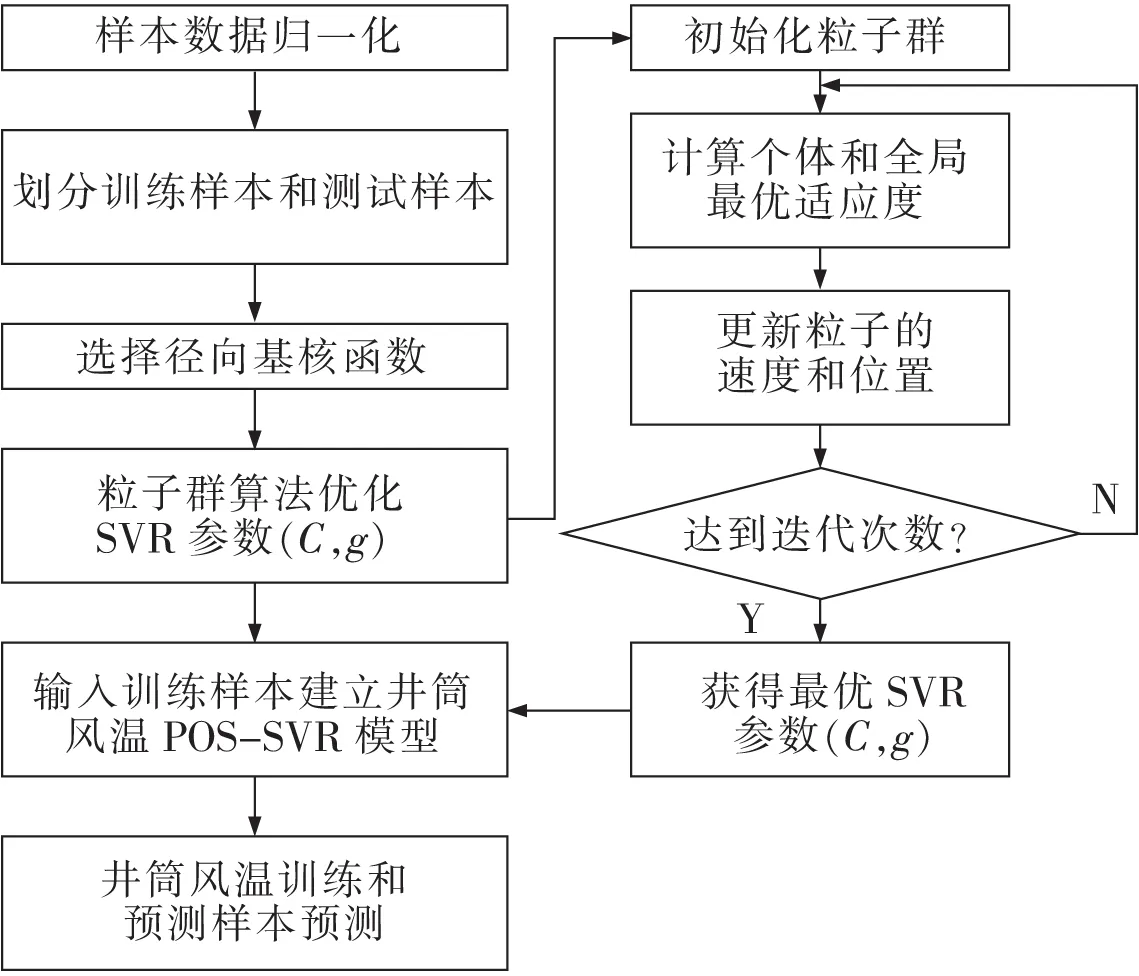
圖1 礦井淋水井筒風溫PSO-SVR預測模型預測過程Fig.1 Prediction process of PSO-SVR prediction model of airflow temperature of shaft with water dropping in mine

3 礦井淋水井筒風溫預測算例分析

3.1 樣本數據

結合礦井生產特點，并參考有關礦井淋水井筒風溫預測研究[16]，綜合分析選取了地面氣候參數及井深作為影響井筒風溫的因素，因此礦井淋水井筒風溫PSO-SVR預測模型的特征向量由地面風溫、地面空氣相對濕度、地面大氣壓、井深構成，輸出變量為井底風溫。選用有關礦井淋水井筒溫度預測研究文獻[11，15，16，19]中近30個礦井共65組實測數據作為樣本數據。樣本數據部分內容見表1。其中前50組實測數據作為訓練集，用于構建模型，后15組實測數據作為測試集，對已訓練好的模型進行預測效果檢驗。

3.2 預測結果對比分析

為研究礦井淋水井筒風溫PSO-SVR預測模型的預測效果，表2列出了其他2種礦井淋水井筒風溫預測模型。利用同樣的訓練和測試樣本數據，將3種礦井淋水井筒風溫預測模型預測精度和預測誤差進行對比。礦井淋水井筒風溫MLR預測模型是根據最小二乘法原理尋求礦井淋水井筒風溫與地面入風氣候參數及井深間的最佳線性回歸函數，實現對礦井淋水井筒風溫的預測。礦井淋水井筒風溫SVR預測模型中，取懲罰因子C為1，核函數參數g為0.25。利用LIBSVM工具箱，編寫PSO算法程序對SVR參數進行尋優，確定最優懲罰因子C為30.1096，核函數參數g為0.010，建立PSO優化后的礦井淋水井筒風溫SVR預測模型。采用上述3種礦井淋水井筒風溫預測模型對訓練和測試樣本進行預測，井底風溫的預測值與其現場實際觀測值散點圖如圖2和圖3所示，圖中橫坐標為井底風溫現場實際觀測值，縱坐標為3種預測模型的井底風溫預測值，直線y=x為預測標準線，分布于該直線上的點的井底風溫預測值等于其現場實際觀測值，即預測誤差為零。

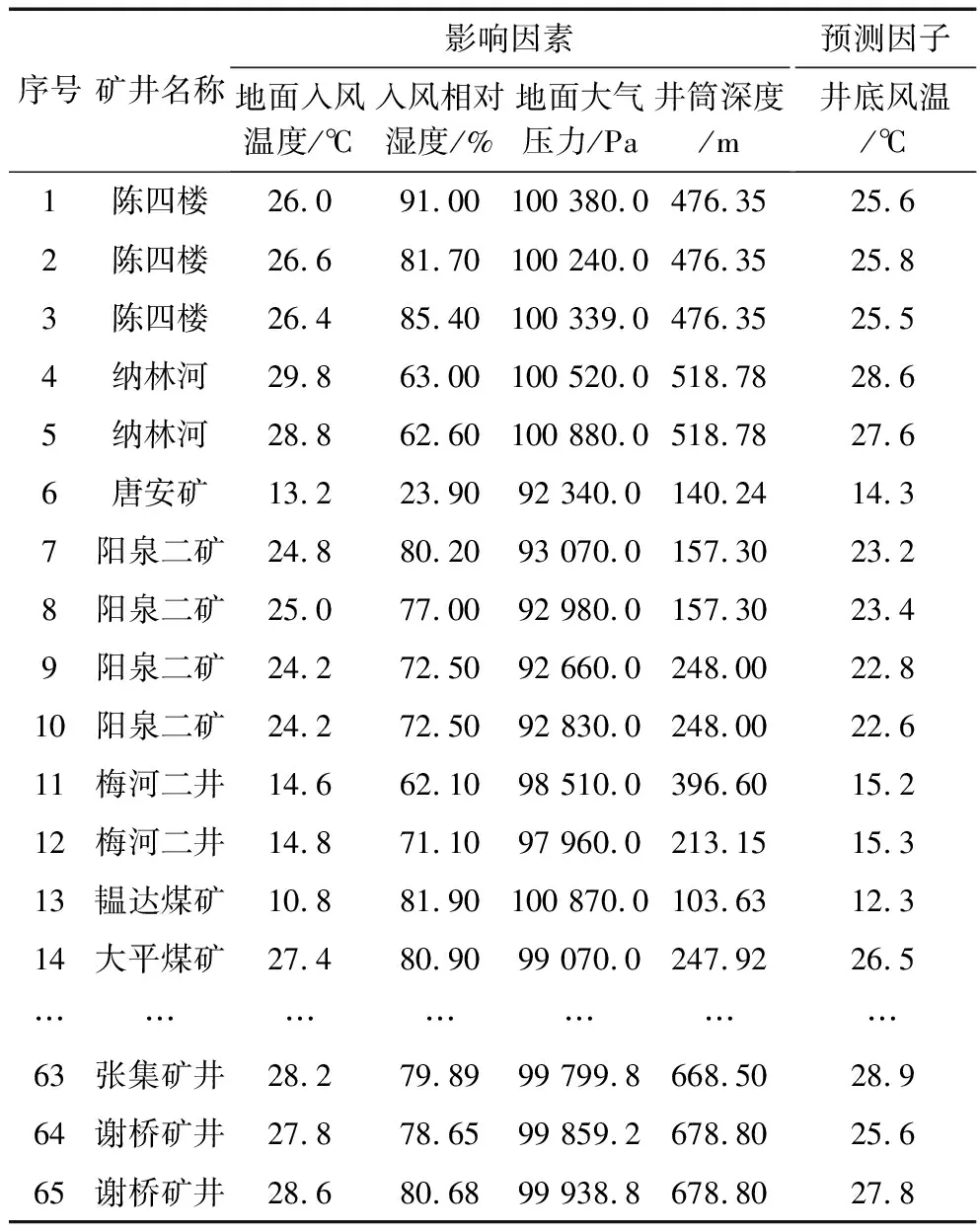
表1 樣本數據(部分)

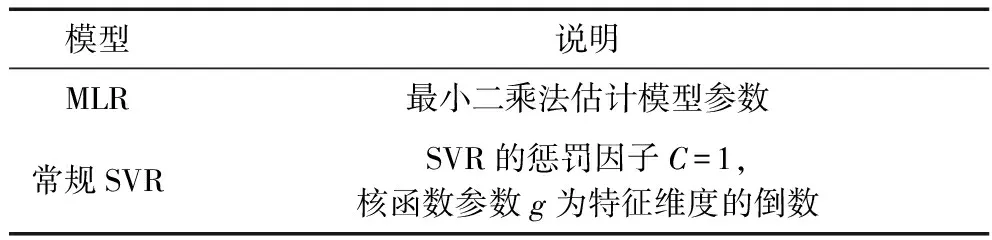
表2 礦井淋水井筒風溫預測模型

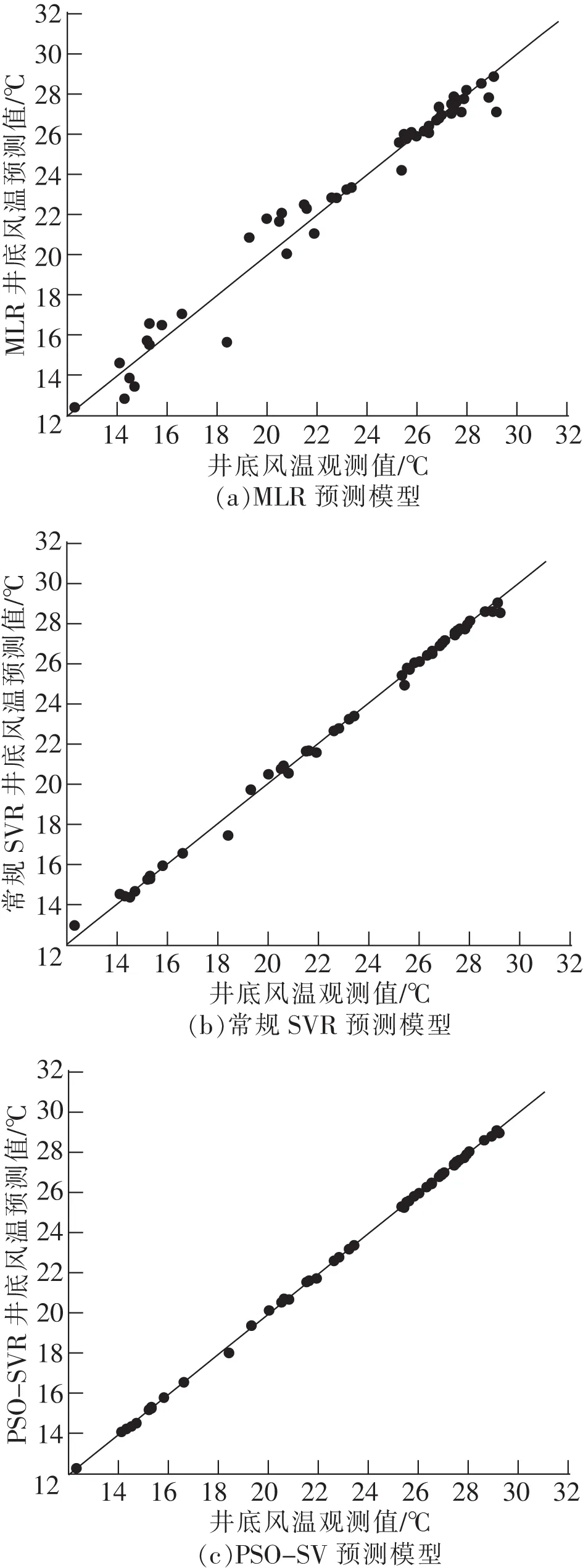
圖2 3種預測模型訓練樣本的預測值和觀測值散點圖Fig.2 Scatter diagram of predicted values and observed values of training samples for the three prediction models

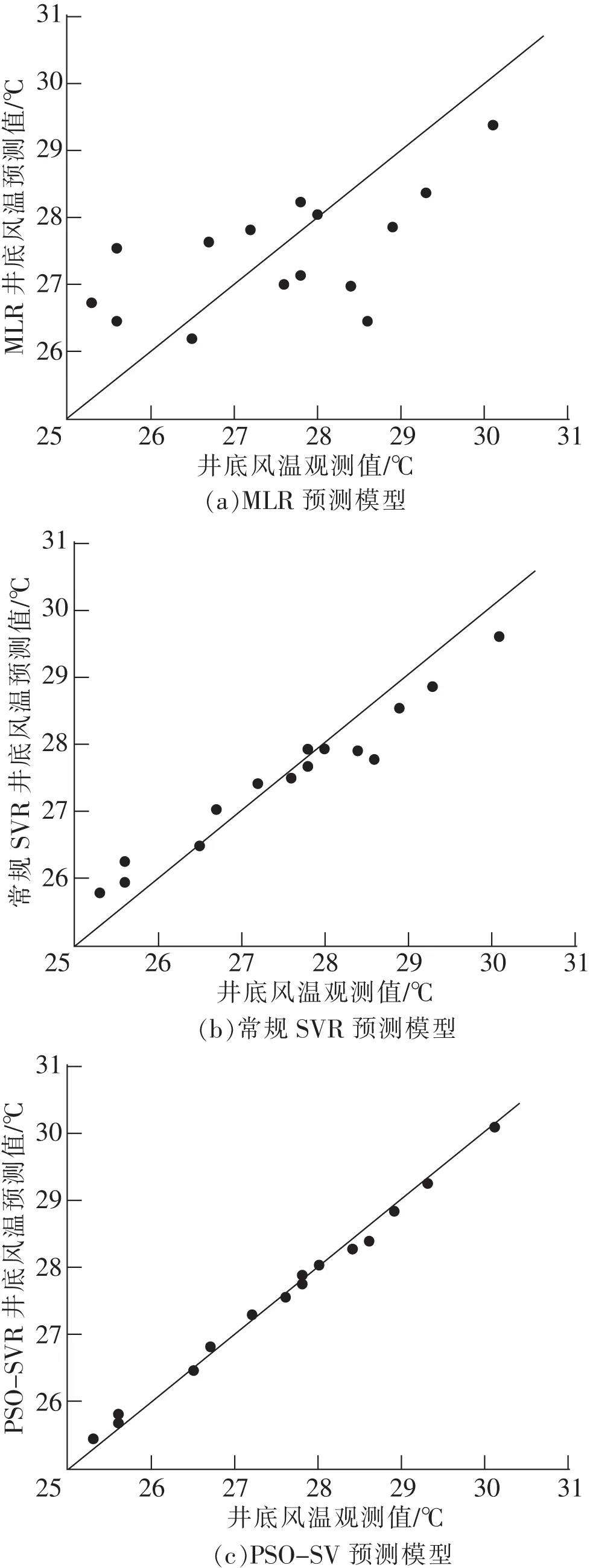
圖3 3種預測模型測試樣本的預測值和觀測值散點圖Fig.3 Scatter diagram of predicted values and observed values of testing samples for the three prediction models

從圖2和圖3可以看出，3種礦井淋水井筒風溫預測模型中，MLR預測模型的訓練和測試樣本的預測與觀測值散點分散于標準線四周，對比MLR預測模型，常規SVR預測模型的預測與觀測值散點較集中分布于標準線周圍，而經過PSO優化后的SVR預測模型的訓練和測試樣本的預測與觀測值散點均集中在標準線附近，說明3種礦井淋水井筒風溫預測模型中，MLR預測模型預測結果偏差最大，PSO-SVR預測模型具有更好的預測精度，更強的泛化性。

圖4給出了3種礦井淋水井筒風溫預測模型的預測值和觀測值的比較曲線。可以看出，3種礦井淋水井筒風溫預測模型下測試樣本的預測值與觀測值曲線的趨勢基本一致，相比于MLR預測模型和常規SVR預測模型，PSO-SVR預測模型的預測值與觀測值曲線更為接近，說明該模型擬合效果更好。

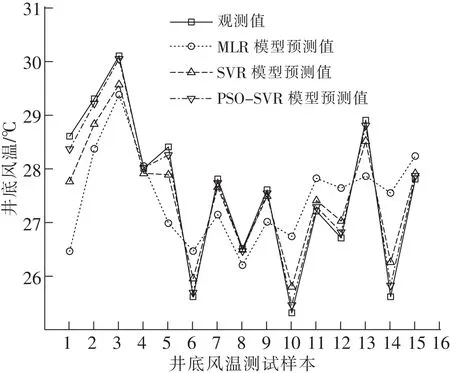
圖4 3種預測模型測試樣本的預測值Fig.4 Prediction values of testing samples for three prediction models

為更直觀地對比3種礦井淋水井筒風溫預測模型的預測效果，表3給出了3種礦井淋水井筒風溫預測模型下測試樣本的預測結果的MAE，MAPE和MSE。

從表3可知，相比于礦井淋水井筒風溫MLR預測模型，常規SVR預測模型的預測結果的MAE與MAPE均提升約63%，MSE提升約85%，說明常規SVR預測模型預測效果好于MLR預測模型；相對于常規SVR預測模型，PSO-SVR預測模型的預測結果的MAE與MAPE均提升約71%，MSE提升約92%，表明在礦井淋水井筒風溫預測中PSO-SVR預測模型具有更好的預測效果，同時也說明了優化SVR參數對提高礦井淋水井筒風溫預測精度有明顯作用。

表3 3種模型預測誤差對比

4 結 論

1)提出了礦井淋水井筒風溫PSO-SVR預測方法。利用粒子群優化算法對支持向量回歸參數進行尋優，建立了礦井淋水井筒風溫PSO-SVR預測模型，實現了對礦井淋水井筒風溫的預測，為礦井風溫預測提供了一種人工智能新方法。

2)礦井淋水井筒風溫PSO-SVR預測模型具有更高的預測精度。對比礦井淋水井筒風溫MLR預測模型的預測結果，SVR預測模型的預測精度有一定提高，而采用PSO對SVR進行參數尋優后的預測模型的預測值更逼近于觀測值，說明礦井淋水井筒風溫PSO-SVR預測模型有更好的預測效果，這也表明了SVR參數優化對于提高礦井淋水井筒風溫預測精度有重要作用。

3)本研究所建立的礦井淋水井筒風溫PSO-SVR預測模型是將地面入風氣候參數及井深作為主要影響因素對礦井淋水井筒風溫進行預測，后續工作可考慮圍巖熱物性參數、風量等因素，建立礦井淋水井筒風溫PSO-SVR預測模型，同時也可嘗試將本研究應用于礦井采掘工作面風溫預測工作當中。