雙級離心風機流場特性分析

連傳平，劉文鋼，喬衛亮

（1. 中遠海運船員管理公司 大連分公司，遼寧大連 116001；2. 大連海事大學 輪機工程學院，遼寧大連 116026）

0 引言

作為一種通用機械，離心風機在各個工業領域具有廣泛的應用。近年來，國內外學者在提升風機效率、降低噪音和風機部件的優化設計方面做了大量工作。席光等[1]利用近似模型方法對葉輪的機械氣動性能進行了優化設計和應用；李景銀等[2]利用該方法對離心葉輪進行了優化設計；梁一凡等[3]利用均勻設計法對高比轉速離心風機進行了分析；簡曉書等[4-5]基于分離葉片對風機氣動性能的影響機理，重點對后向風機葉輪葉片的出口寬度進行了優化計算；POLANSKY等[6]則對前向葉片離心風機的氣動性能建立了預測模型。另外，風機蝸殼對離心風機性能的影響也是學者關注的問題，姜衛生等[7]利用響應面法提出了離心風機蝸殼性能優化方案，王志鵬等[8]則通過建模仿真分析了蝸舌對離心風機流場特性的影響機理；程書山等[9]對蝸殼壁面靜壓分布進行了實驗測量，得到了靜壓分布規律。李曉麗等[10]對離心風機進行了數值計算，并與已有數據進行了比較，指出蝸殼結構的非對稱性會導致葉輪出口流動不均勻。綜上所述，目前針對離心風機的研究大多針對單級離心風機，對多級風機的研究成果相對較少，石碩等[11]基于經驗公式，提出了紡織領域中多級離心風機氣動優化設計方法，楊柳[12]針對懸臂式多級離心風機的工業應用問題提出了相應的設計方法，目前針對雙級離心風機的三維數值分析問題，尚未形成系統的建模方法和成熟的分析方案。

1 風機建模

1.1 建模參數計算

本文擬設計的雙級離心風機的轉速n=1 320 r/min，空氣流量設定為150 m3/h，風機的前后壓差為P=750 Pa，由此可以確定離心風機的比轉數：

根據沈陽鼓風機研究所試驗統計資料，離心風機葉片的進出口安裝角分為α=27.1°和β=90°，由于機翼型葉片壓力系數與出口安裝角成線性關系，壓力系數取值為P=0.65，由此，可以計算得到葉輪圓周速度u2和葉輪外徑分別為

將式（2）、式（3）和式（5）依次代入式（4），可得葉片進口直徑為0.11 m。一般情況下考慮分離影響，葉輪進口直徑與略小于葉片進口直徑，D1＝(1.00～1.05)D0，因此取葉輪進口直徑為0.104 m。由此，可以計算葉輪的葉片數：

1.2 幾何模型

雙級離心風機中需要幾何建模的結構主要包括：一級葉輪、擴壓器、彎管、回流器、二級葉輪和蝸殼。本論文在CFturbo軟件平臺下進行幾何建模，各個結構部件的幾何參數見表1。

表1 雙級離心風機結構部件的幾何參數

續表1：

根據確定的雙級風機各結構部件的幾何參數，在CFturbo軟件平臺下，建立的幾何模型見圖1。

圖1 雙級離心風機的幾何模型

2 網格劃分與仿真環境

2.1 生成網格

將CFturbo生成的文件導入ICEM CFD中進行網格劃分，采用非結構化四面體網格，第一級風機網格數約為119萬，數量相對較多；第二級風機網格數約為90萬，生成的網格見圖2。

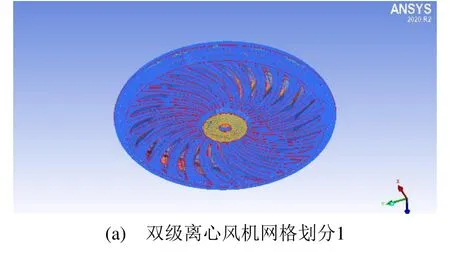
圖2 雙級離心風機網格劃分

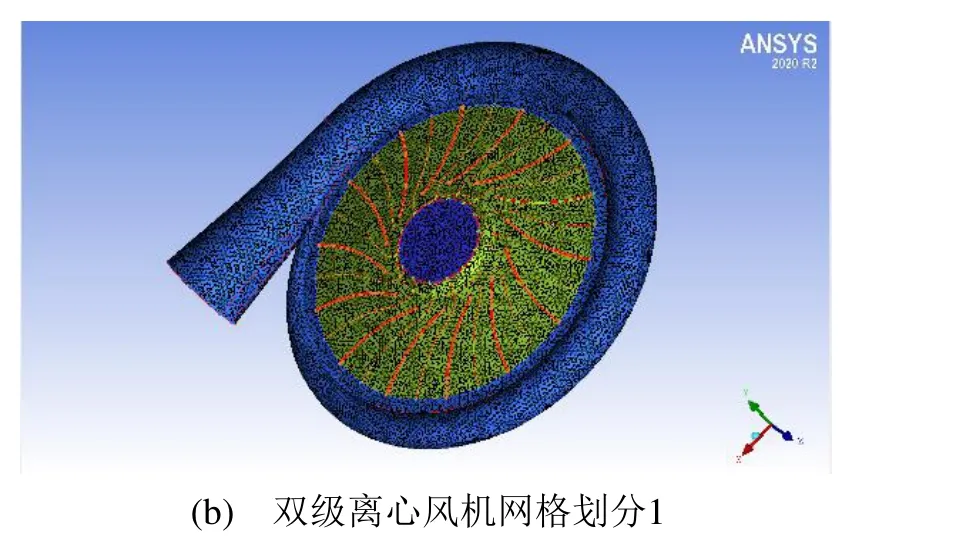
圖2 雙級離心風機網格劃分（續）

2.2 仿真環境

雙級離心風機進口處的氣體設為20 ℃下的空氣，進口壓力為大氣壓，即0.1 MPa，空氣密度為1.2 kg/m3，葉輪旋轉方向為順時針方向，空氣動力效率設為100%，不考慮空氣泄漏的影響[13]。風機內的湍流模型設置為標準k-ε模型，風機進口處的空氣流速為7.44 m/s，風機內部壁面為光滑壁面，在風機出口處定義靜壓和其他變量。在求解器設置方面，選擇SIMPLE格式和2階迎風的離散格式，精度為2階精度。考慮到本文第一級風機網格數量較多，計算時間長而且不是很穩定，適當減小了松弛因子的設定值。

2.3 網格收斂性判斷

仿真環境設定之后，通過運行求解器對計算守恒變量的殘差進行計算，以便判斷網格收斂性。本文設定殘差低于初始殘差0.001以下為滿足計算精度要求。第一級和第二級風機的殘差曲線見圖3。第一級風機網格大約在接近2 000步時計算完成，第二級風機網格大約在1 600步時計算完成，表明本文劃分的風機網格符合預期計算要求。

圖3 雙級離心風機的殘差曲線

3 仿真結果分析

3.1 葉輪內部流場分析

3.1.1 壓力分布

依托于ANSYS仿真平臺，得到第一級和第二級葉輪的壓力分布情況見圖4和圖5。其中，靜壓是單位體積的氣體所具有的勢能，全壓是動壓和靜壓的代數和，代表著氣體內含有的總能量，全壓和靜壓的差值表征動壓的大小。通過對比圖4和圖5中靜壓和全壓云圖可以發現：葉輪出口處二者差異較大，表明出口處的動壓較大。另外，在風機內部，壓力從進口到出口逐漸變大，在每塊葉片上的靜壓值和全壓值沿著工作面和非工作面逐漸增大，到出口達到最大值，并且葉片工作面的壓力值要比非工作面的靜壓值大，流道中間的壓力值要低于兩側的壓力。葉輪流道內壓力最小值在葉片進口非工作面上，流道內壓力最大值在葉片的出口的壓力面上，與文獻[14]的分析計算結果基本一致。

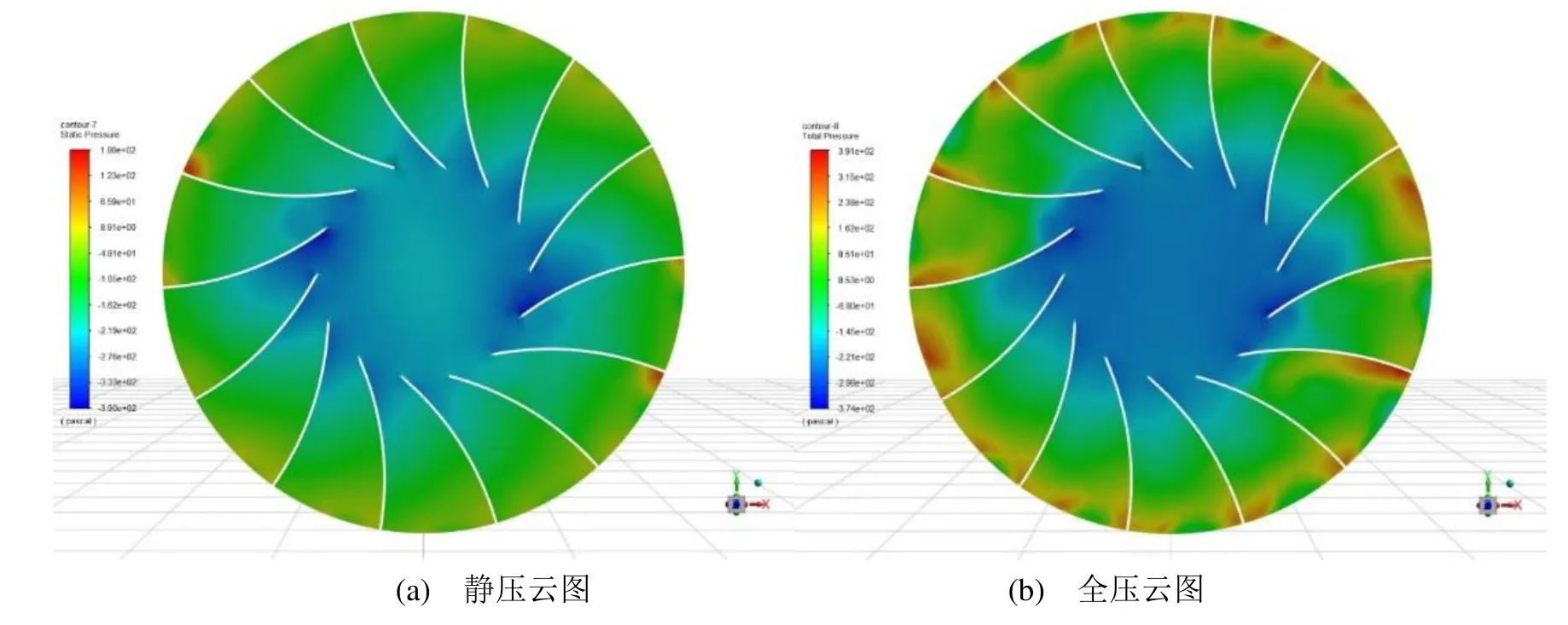
圖4 第一級葉輪壓力云圖

圖5 第二級葉輪壓力云圖

3.1.2 速度分布

第一級風機和第二級風機的速度云圖分別如圖6(a)圖6(b)所示，對于兩級葉輪，在吸力側面，由于氣流先收斂后擴壓，氣流速度在葉輪進口到出口的過程中不斷地增大，一直到出口時速度最大。而且在葉輪流道中，離葉片越近流動速度越低，但是在葉片的工作面流速比在非工作面的流速較高，在其他位置的流動速度相比于葉片位置速度較高。在蝸殼內，由于體積突然增大，流動速度降低，壓力升高。

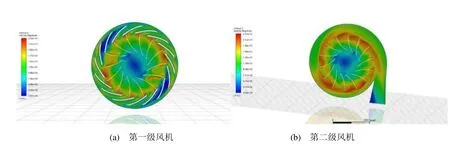
圖6 葉輪內速度云圖

3.2 擴壓器內流場特性

擴壓器內的靜壓和全壓分布情況分別如圖7(a)和圖7(b)所示。擴壓器內部有葉片的部分沿著葉片方向壓力逐漸增大，到達出口部分即無葉片部分壓力達到最大值。因為在葉片部分容積慢慢沿著葉片增大，所以擴壓過程主要在該部分完成。在設計中擴壓器存在一些缺陷，在于葉輪的匹配不夠特別合理，擴壓器與葉輪之間的間隙很小，導致流場中的壓力和速度會在部分中過高或過低。葉輪出口與擴壓器葉片的前緣之間的間隙決定著離開葉輪氣流中射流和尾跡的互相摻雜過程還有氣體泄露的問題。擴壓器葉片前緣與葉輪出口之間的距離增大，從葉輪出來的氣流速度在擴壓器沒有葉片部分下降的特別緩慢，間隙的增大造成延長氣體進入葉道的時間，同時增大的間隙增加了氣體的摩擦損失，氣體在進入葉道后能量減少，同樣的擴壓器對于葉輪做功少的氣體是不適用的，因此出現了速度分離現象，而且減速緩慢，增壓效果不好。

圖7 擴壓器內流場特性

3.3 回流器內流場特性

回流器內流場的靜壓和全壓分布情況分別見圖8。當氣體從彎管中出來后進入回流器中壓強下降，這是由于氣體從體積較大的部位進入狹長的流道中氣體的壓強能轉換為速度能，速度變快，壓強減小。由于回流器設計為翼型，葉片之間的容積沿葉片不會變換太多，壓強也不會有很大變化，使擴壓器出來的氣體壓強下降不會太多。

圖8 回流器內的壓力分布

回流器內流場的速度分布情況見圖9，回流器進口氣體流速非常沒有規律，原因主要在于雙級離心風機中，第一級葉輪、徑向擴壓器的負荷較高，導致徑向擴壓器出口的流動并不均勻；與此同時，經過擴壓器的氣流需要經過彎管進行180°左右的轉彎才會到達回流器的進口，在彎道中與2個端壁存在摩擦現象導致能量損失。葉片對回流器的流動同樣存在影響，隨著葉片數的增加，回流器的出口氣流角的分布會趨于均勻。這現象說明：葉片數的增加會對回流器內部的二次流起到一定的作用，但是，經過試驗可以得知，無限制的增加葉片數量并不能改變回流器內部的結構，回流器內部的二次流依然還很強烈，所以，依靠增加葉片數來抑制回流器內部的二次流現象的作用相對有限。

圖9 回流器速度云圖

3.4 蝸殼內流場特性

第二級風機靜壓云圖如圖5(a)最外一周便是蝸殼的靜壓分布, 內經過定子出來的氣流流動方向基本沿著蝸殼彎壁流動著，兩者之間沒有大的沖擊，這表明蝸殼的設計比較合理，由于蝸殼內存在流動損失，總壓沿著流動方向會減小。同時，可以看出在蝸舌附近的速度云圖6(b)中經過蝸舌遲滯點分離的兩部分流動中，向上流入蝸室的一部分速度較高，像出口流出的速度較低，與文獻[15]的計算結果基本一致；在出口段靠近蝸舌所在壁的氣流速度明顯要比另一側的流動速度低。

3.5 全壓驗證

根據仿真計算結果，第一級和第二級風機進出口的全壓數值見表2。

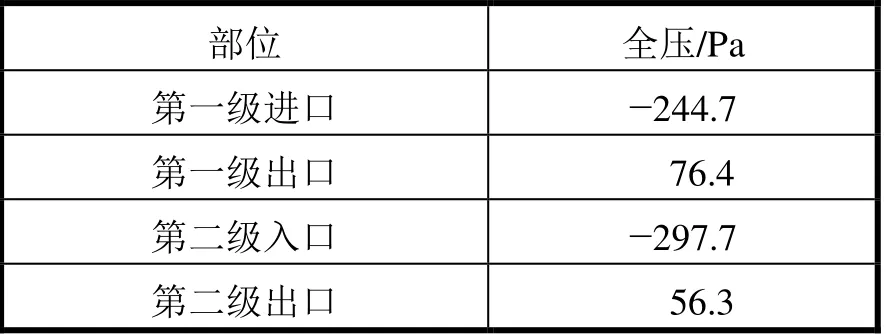
表2 風機進出口全壓數值

仿真計算后對兩級風機進出口全壓進行檢測計算看是否能夠到達預期的要求。風機的全壓公式為出口全壓減去進口全壓，由表2中的兩級進出口全壓數值計算得出，第一級風機全壓值為321 Pa，第二級風機全壓值為354 Pa。兩級風機全壓差相加和為675 Pa，原定風機要求壓差為650 Pa，誤差約為3%，可以在接受范圍內。

4 結論

本文以轉速1 320 r/min，流量150 m3/h，壓差650 Pa的雙級離心風機為設計目標，在對相關設計參數進行理論計算的基礎上，分別對雙級離心風機的葉輪、擴壓器、回流器、彎道和蝸殼進行幾何設計和建模。將幾何模型導入Fluent仿真平臺，以設計轉速和流量為輸入條件，計算得到風機先后壓差為675 Pa，誤差率為3%，符合設計要求。