變壓器寄生參數對LLC 諧振變換器的影響

張 平，丁 潔，孫 莉

（1. 海軍裝備部駐上海地區軍事代表室，上海 200031；2. 上海船舶設備研究所，上海 200031）

0 引言

隨著電力電子變換技術的發展，市場對高開關頻率、高效率、高功率密度的電力電子變換器需求越來越廣。其中，LLC諧振變換器通過合理的參數設計，能夠實現初級側MOSFET的零電壓開通和次級側整流二極管的零電流關斷，從而降低變換器的開關損耗，提高其效率和功率密度，因而得到越來越廣泛的應用[1]。

LLC諧振變換器在進行穩態特性分析時，通常對理想變壓器進行分析，忽略其寄生參數的影響。而實際應用中，隨著開關頻率的提高，寄生參數的影響難以忽略[2-3]。

本文對半橋LLC諧振變換器中變壓器寄生參數的影響進行了理論分析和試驗驗證，對半橋LLC諧振變換器的實際應用具有參考意義。

1 半橋LLC 諧振變換器寄生參數

圖1為半橋LLC諧振變換器的電路拓撲，包括初級側開關網絡、諧振網絡和次級側整流濾波網絡。圖1中，Vin為半橋LLC諧振變換器的輸入電壓，V0為輸出電壓。開關網絡包括兩只開關管Q1、Q2及其反并二極管D1、D2；諧振網絡包括串聯諧振電感Lr、串聯諧振電容Cr和并聯諧振電感Lm，其中Lr可以用變壓器的漏感來實現，Lm可以用變壓器的勵磁電感來實現；次級側整流濾波網絡包括整流二極管DR1、DR2和輸出濾波電容Co，RLd為負載電阻。

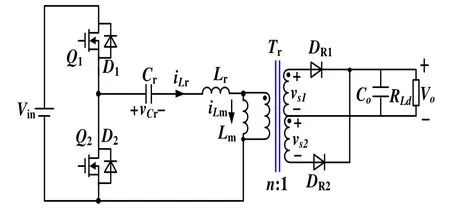
圖1 理想半橋LLC 諧振變換器電路拓撲

基波分析法在對諧振變換器進行穩態分析時被廣泛應用。故對理想半橋LLC諧振變換器進行穩態分析，得出其穩態模型見圖2[4]。圖中，Req為等效電阻。

圖2 理想半橋LLC 諧振變換器等效模型

此時變換器在不同負載下的增益曲線見圖3，其中，fr為變換器諧振頻率。當變換器的負載較輕時，最大增益超過1[5]。

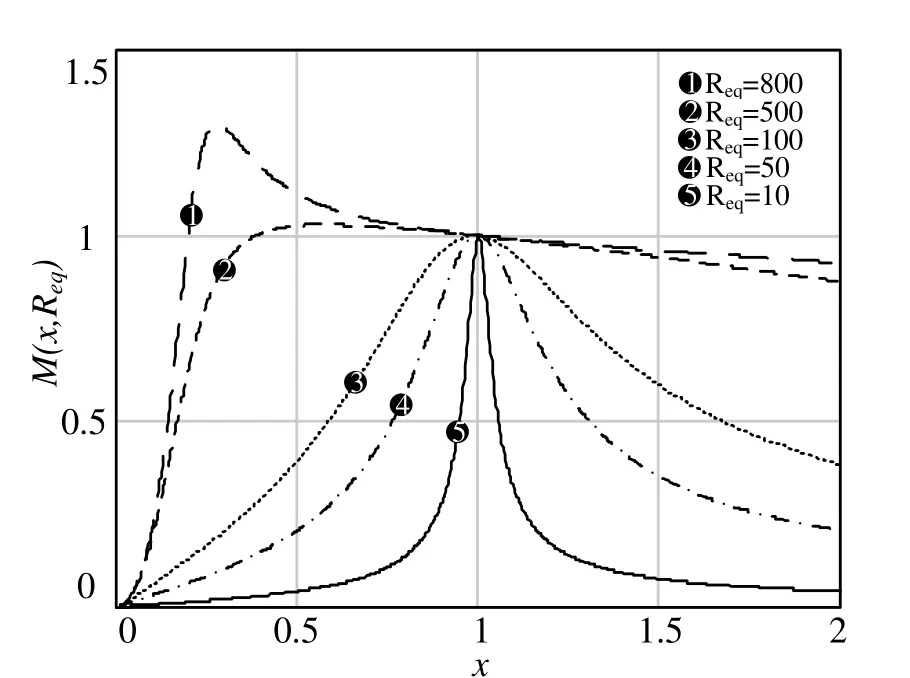
圖3 理想半橋變換器的增益曲線

實際上半橋LLC諧振變換器的寄生參數還包括初級側MOSFET的結電容Coss、次級側整流二極管結電容Cos、變壓器分布電容CTR、變壓器初級側漏感Llkp（可作為諧振電感Lr）以及次級側漏感Llks1、Llks2，見圖4[6]。

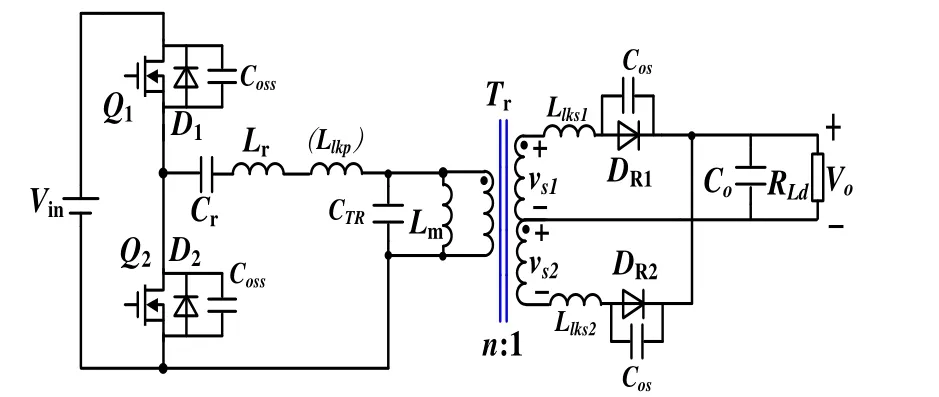
圖4 考慮寄生參數的半橋LLC 諧振變換器拓撲

開關器件結電容在器件選型后可確定，本文主要討論變壓器寄生參數對半橋LLC諧振變換器造成的影響。

2 變壓器漏感的影響

變壓器實際繞制時，初、次級側均存在漏感，初級側的漏感可作為諧振電感的一部分，因此，主要考慮變壓器的次級側漏感Ls對變換器特性的影響。

2.1 原理分析

若考慮變壓器的次級側漏感，則變換器的等效模型見圖5[7-8]。

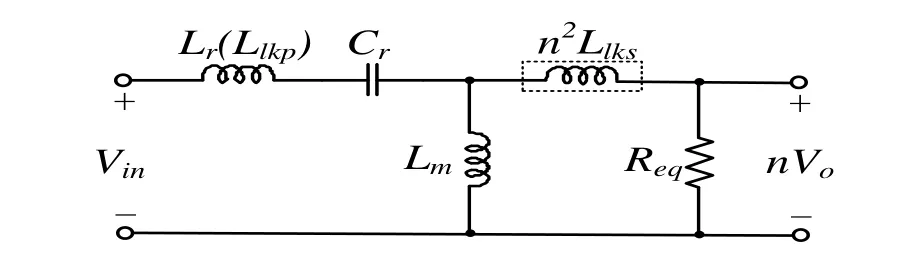
圖5 考慮次級側漏感等效模型

式中：Ls為次級側漏感，μH，折合至原邊值為n2Llks。

兩個人聊得很少。似乎沒有可聊的話題，又似乎話題太多，卻總是尋不到進入的切點。只好聊莫高，聊阿芳，靜秋說，她現在和阿芳仍然有聯系。

作出變換器的增益曲線見圖6，可知在考慮變壓器的次級側漏感之后，增益曲線表現為諧振頻率點左移，尤其是當負載較重時，曲線的左移更加明顯。

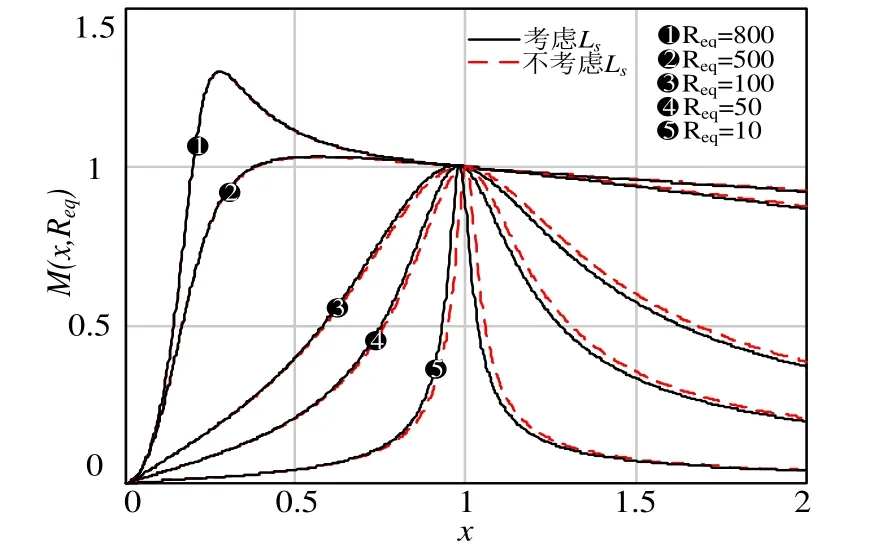
圖6 考慮變壓器漏感的增益曲線

由于本文中分析的半橋LLC諧振變換器采用全波整流方式，變壓器次級側有2個繞組，故對變壓器次級側漏感的影響作進一步分析。

當開關管Q1開通時，其工作模態見圖7，諧振電感電流開始以近似正弦規律增大，次級側二極管DR1導通。此時除諧振電感Lr、諧振電容Cr和勵磁電感Lm外，次級側漏感Llks1也參與諧振。

圖7 變換器上管開通時工作模態

而當勵磁電感電流線性下降至0之前，開關管Q2開通，其工作模態見圖8，諧振電感電流開始以近似正弦規律減小，次級側二極管DR2導通。此時除諧振電感Lr、諧振電容Cr和勵磁電感Lm外，次級側漏感Llks2也參與諧振。

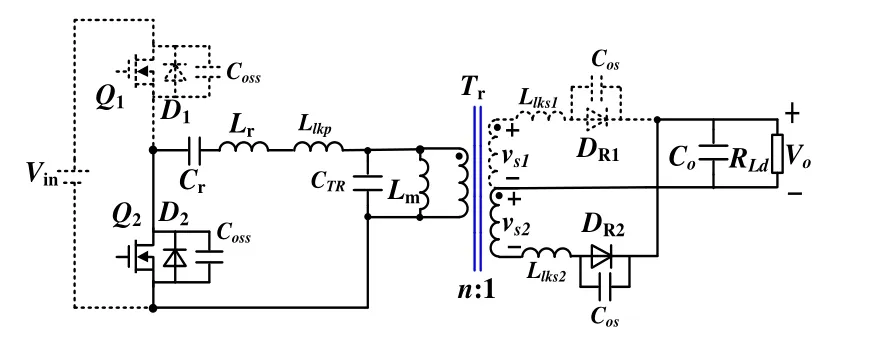
圖8 變換器下管開通時工作模態

通過以上分析，可知LLC諧振變換器的變壓器次級側漏感會對變換器的增益和工作模態造成影響，特別是次級側采用全波整流時，2個繞組存在2個漏感，會在變換器不同工作模態時分別造成影響。

2.2 試驗驗證

為了驗證理論分析的正確性，對半橋LLC諧振變換器進行了開環試驗驗證。試驗條件為：輸入電壓Vin為680 V，輸出電壓Vo為150 V，輸出功率Po為2kW，工作頻率fs為110 kHz，諧振電容200 nF，變壓器的勵磁電感Lm為406 μH，諧振電感Lr用變壓器的漏感來實現[9]。

變壓器1采用逐層間繞法，見圖9(a)，是將初、次級線圈分別繞制在奇數層和偶數層，可在層間加墊絕緣紙，優點是繞制相對簡單，且兩線圈間耐壓較高，缺點是初、次級的耦合相對較差。

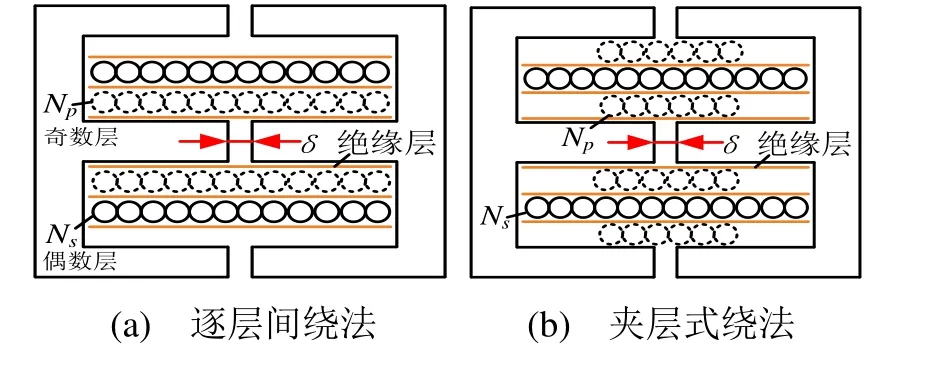
圖9 變壓器繞制方式

變壓器1的初級側漏感為4.975 μH，次級側漏感分別為3.53 μH、1.44 μH。

采用變壓器1時，諧振電感電流波形如圖10所示。由圖10可知，變壓器次級側2個繞組漏感不一致時，會導致不同工作模態時諧振頻率不同，諧振電感電流波形正負半周不對稱。

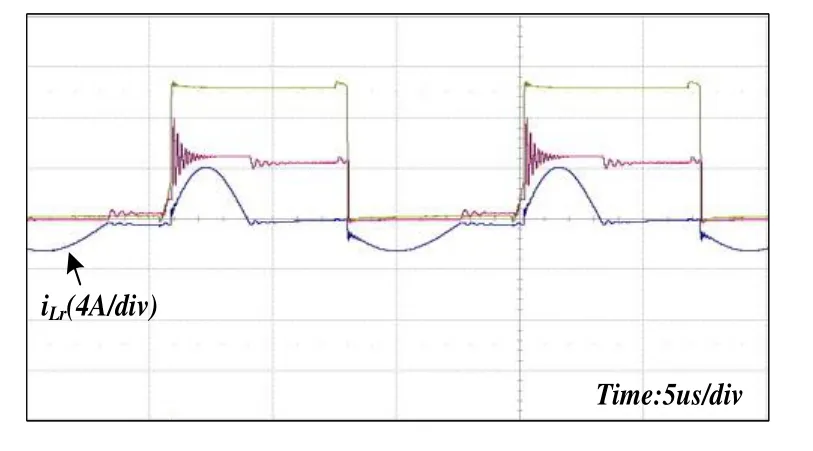
圖10 采用變壓器1 時的波形

變壓器2采用夾層式繞法，如圖9(b)所示，即三明治繞法，是指將初級繞組分成2部分，先繞制一半，接著繞制次級線圈，最后再繞制初級線圈的另一半。這種方法增大了初級與次級的有效耦合面積，減小了變壓器漏感，同時由于在初級繞組間加入次級繞組，也減小了初級繞組的層間分布電容，且只在初級繞組中多一個接頭，工藝簡單，便于批量生產。

變壓器2的初級側漏感為6.81 μH，次級側漏感分別為0.83 μH、0.83 μH。采用變壓器2時，諧振電感電流波形見圖11。由圖11可知：變壓器次級側2個繞組漏感基本一致，諧振頻率基本一致，諧振電感電流波形正負半周對稱。

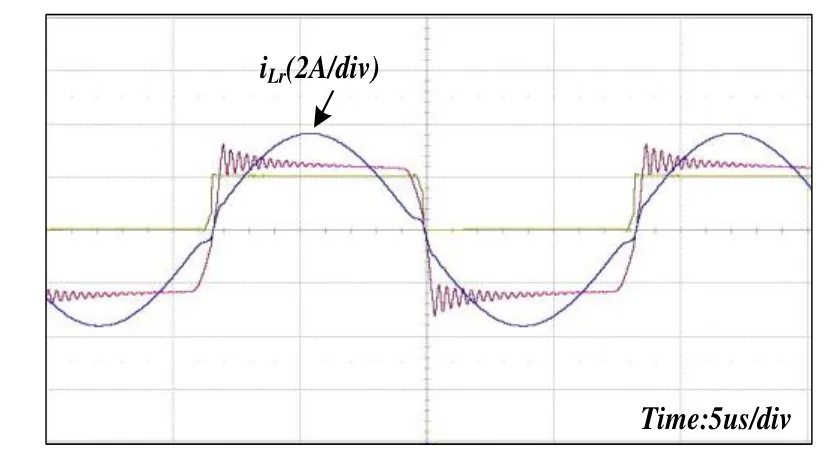
圖11 采用變壓器2 時的波形

故半橋LLC諧振變換器采用全波整流方式時，需特別注意變壓器的繞制方式，保持次級側2個漏感一致。

3 變壓器分布電容的影響

變壓器的分布電容在實際繞制中也不可避免，主要分為繞組匝間電容、層間電容、繞組電容和雜散電容等。

3.1 原理分析

考慮變換器的分布電容，變換器的等效電路見圖12。

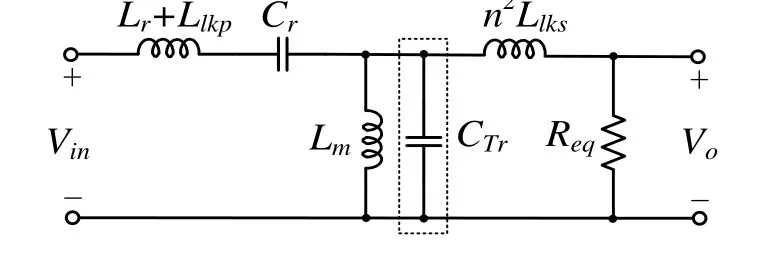
圖12 考慮分布電容等效模型

式中：CTr為變壓器分布電容，pF。

根據式（3）作出增益曲線見圖13。一般情況下，變壓器的分布電容為pF級。根據增益曲線可以看出，變壓器的分布電容會造成變換器在低頻段的增益下降以及高頻段的增益曲線上抬。特別是在負載較輕時，分布電容的影響會更嚴重。

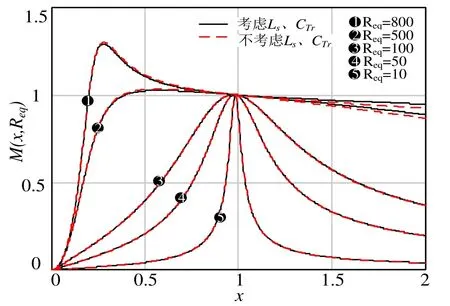
圖13 考慮變壓器寄生電感、分布電容增益曲線

3.2 試驗驗證

為了驗證變壓器分布電容的影響，在空載情況下，對半橋LLC諧振變換器試驗驗證。試驗條件為：輸入電壓Vin為680 V，輸出電壓Vo為150 V，輸出功率Po為2 kW，工作頻率fs為110 kHz，諧振電容200 nF，變壓器的勵磁電感Lm為406 μH，諧振電感Lr即初級側漏感為6.81 μH，次級側漏感均為0.83 μH。

當變壓器分布電容較大時，由于分布電容參與諧振，空載時諧振電感電流、次級側二極管電壓波形見圖14，振蕩嚴重。

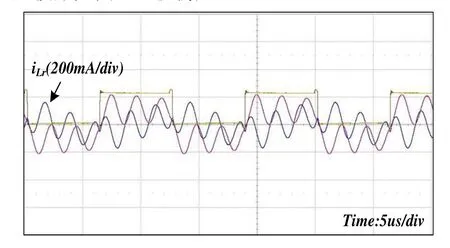
圖14 分布電容較大時空載波形

雖然變壓器分布電容不可避免，但可通過以下途徑減小其大小：

1）通過選擇介電常數較低的漆包線、增大繞組匝間的距離、多槽骨架分段繞制減小繞組匝間電容。

2）通過增大繞組層間距離（如：采用三重絕緣線）、選擇繞線面積較寬的骨架、采用交叉堆疊繞法來減小層間電容。

3）通過增加絕緣厚度、增加法拉第屏蔽層來減小繞組電容。

根據以上途徑將變壓器分布電容減小后，空載時諧振電感電流、次級側二極管電壓波形見圖15，其造成的諧振明顯減小。

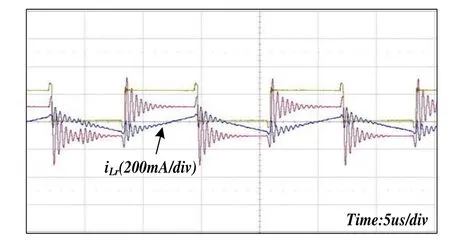
圖15 分布電容較小時空載波形

4 結論

針對LLC諧振變換器在進行穩態特性分析時，通常對理想變壓器進行分析，忽略其寄生參數的影響的問題，本文對LLC諧振變換器中的變壓器寄生參數造成的影響進行了理論分析和試驗驗證，對LLC諧振變換器的實際應用具有參考意義。